湘教版九年级上《第三章图形的相似》单元评估试卷(有答案)
文档属性
| 名称 | 湘教版九年级上《第三章图形的相似》单元评估试卷(有答案) |  | |
| 格式 | zip | ||
| 文件大小 | 152.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-01-05 18:42:52 | ||
图片预览


文档简介
湘教版九年级数学上册 第三章 图形的相似 单元评估检测试卷
一、单选题(共10题;共30分)
1.如图所示,在△ABC中D为AC边上一点,若∠DBC=∠A , BC=3,AC=6,则CD的长为( )
/
A.?1??????????????????????????????????????????B.?2??????????????????????????????????????????C.?/??????????????????????????????????????????D.?/
2.如图,直线
??
1
∥
??
2
∥
??
3
,直线AC分别交
??
1
,
??
2
,
??
3
于点A,B,C;直线DF分别交
??
1
,
??
2
,
??
3
于点D,E,F.AC与DF相交于点G,且AG=2,GB=1,BC=5,则
????
????
的值为( ??) /
A.?
1
2
??????????????????????????????????????????/B.?
3
5
??????????????????????????????????????????/C.?
2
5
??????????????????????????????????????????/D.?2
3.若两个图形位似,则下列叙述不正确的是(??? )
A.?每对对应点所在的直线相交于同一点??????????????????/B.?两个图形上的对应线段之比等于位似比 C.?两个图形上的对应线段必平行?????????????????????????????/D.?两个图形的面积比等于位似比的平方
4.如图,在△ABC中,点D、E分别在边AB、AC上,下列条件中不能判断△ABC∽△AED的是(? )
/
A.∠AED=∠B B.∠ADE=∠C C.
????
????
=
????
????
D.
????
????
=
????
????
5如图,在平行四边形ABCD中,E为AD的中点,△BCF的面积为4,则△DEF的面积为(???? ) /
A.?1???????????????????????????????????????????/B.?2???????????????????????????????????????????/C.?3???????????????????????????????????????????/D.?4
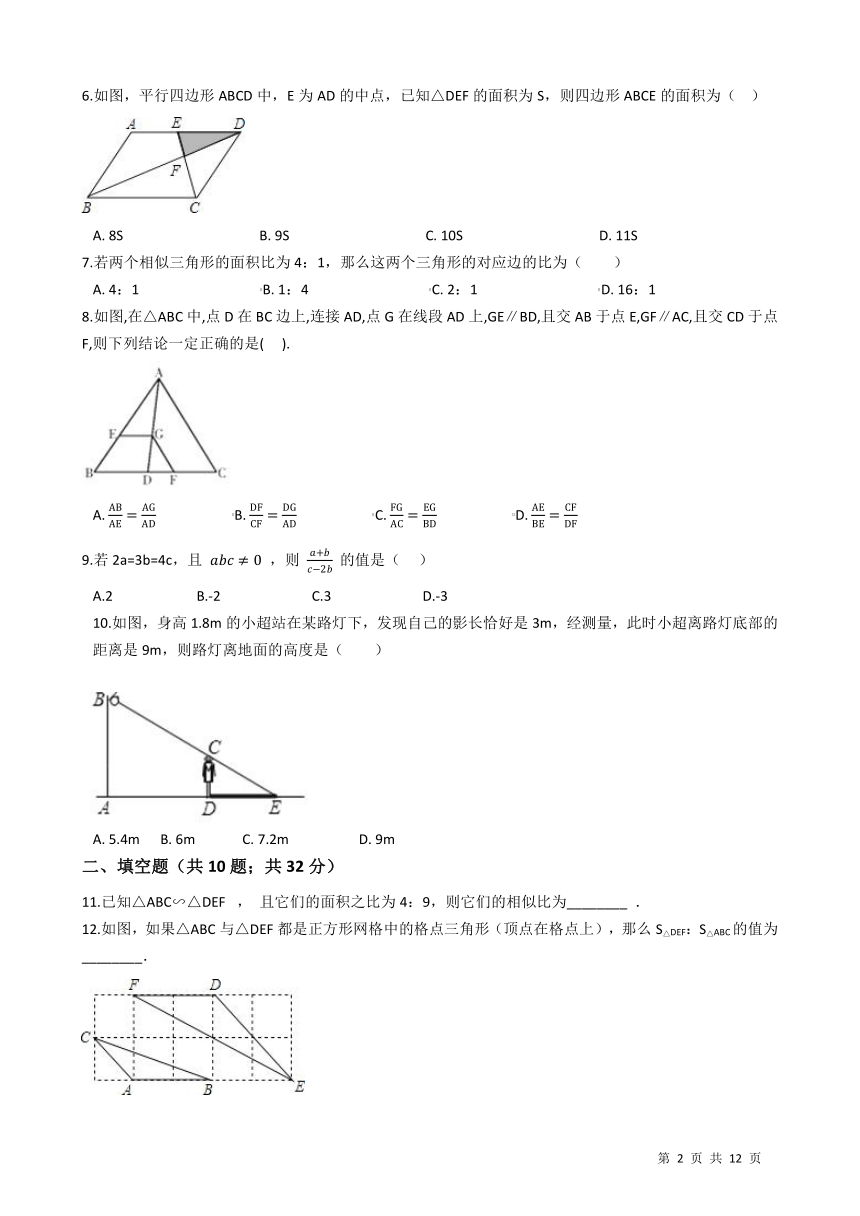
6.如图,平行四边形ABCD中,E为AD的中点,已知△DEF的面积为S,则四边形ABCE的面积为(?? ) /
A.?8S???????????????????????????????????????/B.?9S???????????????????????????????????????/C.?10S???????????????????????????????????????/D.?11S
7.若两个相似三角形的面积比为4:1,那么这两个三角形的对应边的比为( )
A.?4:1???????????????????????????????????/B.?1:4???????????????????????????????????/C.?2:1???????????????????????????????????/D.?16:1
8.如图,在△ABC中,点D在BC边上,连接AD,点G在线段AD上,GE∥BD,且交AB于点E,GF∥AC,且交CD于点F,则下列结论一定正确的是(??? ). /
A.?
AB
AE
=
AG
AD
??????????????????????/B.?
DF
CF
=
DG
AD
??????????????????????/C.?
FG
AC
=
EG
BD
??????????????????????/D.?
AE
BE
=
CF
DF
9.若2a=3b=4c,且 ??????≠0 ,则
??+??
???2??
的值是( ???)
A.2 B.-2 C.3 D.-3 10.如图,身高1.8m的小超站在某路灯下,发现自己的影长恰好是3m,经测量,此时小超离路灯底部的距离是9m,则路灯离地面的高度是( )
/
A.?5.4m ???/B.?6m ??/C.?7.2m ??/D.?9m
二、填空题(共10题;共32分)
11.已知△ABC∽△DEF? , 且它们的面积之比为4:9,则它们的相似比为________ .
12.如图,如果△ABC与△DEF都是正方形网格中的格点三角形(顶点在格点上),那么S△DEF:S△ABC的值为________. /
13.如图,小明用长为3m的竹竿CD做测量工具,测量学校旗杆AB的高度,移动竹竿,使竹竿与旗杆的顶端C、A与O点在一条直线上,则根据图中数据可得旗杆AB的高为________m. /
14.如图,在△ABC中,∠C=90°,D是AC上一点,DE⊥AB于点E,若AC=8,BC=6,DE=3,则AD的长为 ???????????? .
15.如图,在△ABC中,AD平分∠BAC,与BC边的交点为D,且DC=
1
3
BC,DE∥AC,与AB边的交点为E,若DE=4,则BE的长为________. ?/ ?16.如图,AC∥EF∥DB,若AC=8,BD=12,则EF=________. /
17.矩形纸片ABCD,AB=9,BC=6,在矩形边上有一点P,且DP=3.将矩形纸片折叠,使点B与点P重合,折痕所在直线交矩形两边于点E,F,则EF长为________.
18.如图,在△ABC中,点E,F分别是AC,BC的中点,若S四边形ABFE=9,则S三角形EFC=________. /
19.如图,△ABC中,点D,E分别在边AB,BC上,DE∥AC.若BD=4,DA=2,BE=3,则EC=________. /
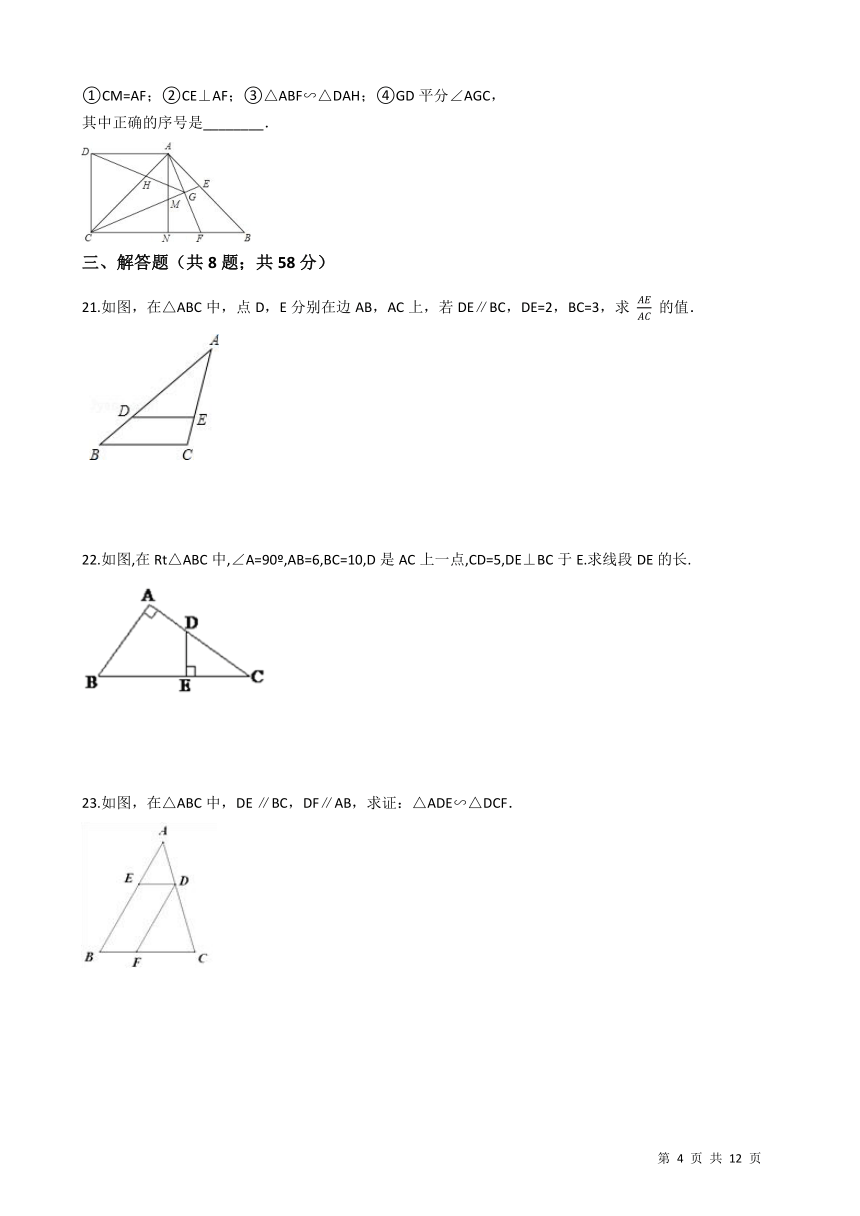
20.如图,在四边形ABCD中,AD∥BC,∠BCD=90°,∠ABC=45°,AD=CD,CE平分∠ACB交AB于点E,在BC上截取BF=AE,连接AF交CE于点G,连接DG交AC于点H,过点A作AN⊥BC,垂足为N,AN交CE于点M.则下列结论: ①CM=AF;②CE⊥AF;③△ABF∽△DAH;④GD平分∠AGC, 其中正确的序号是________. /
三、解答题(共8题;共58分)
21.如图,在△ABC中,点D,E分别在边AB,AC上,若DE∥BC,DE=2,BC=3,求
????
????
的值.
/
22.如图,在Rt△ABC中,∠A=90o,AB=6,BC=10,D是AC上一点,CD=5,DE⊥BC于E.求线段DE的长. /
23.如图,在△ABC中,DE ∥BC,DF∥AB,求证:△ADE∽△DCF. /
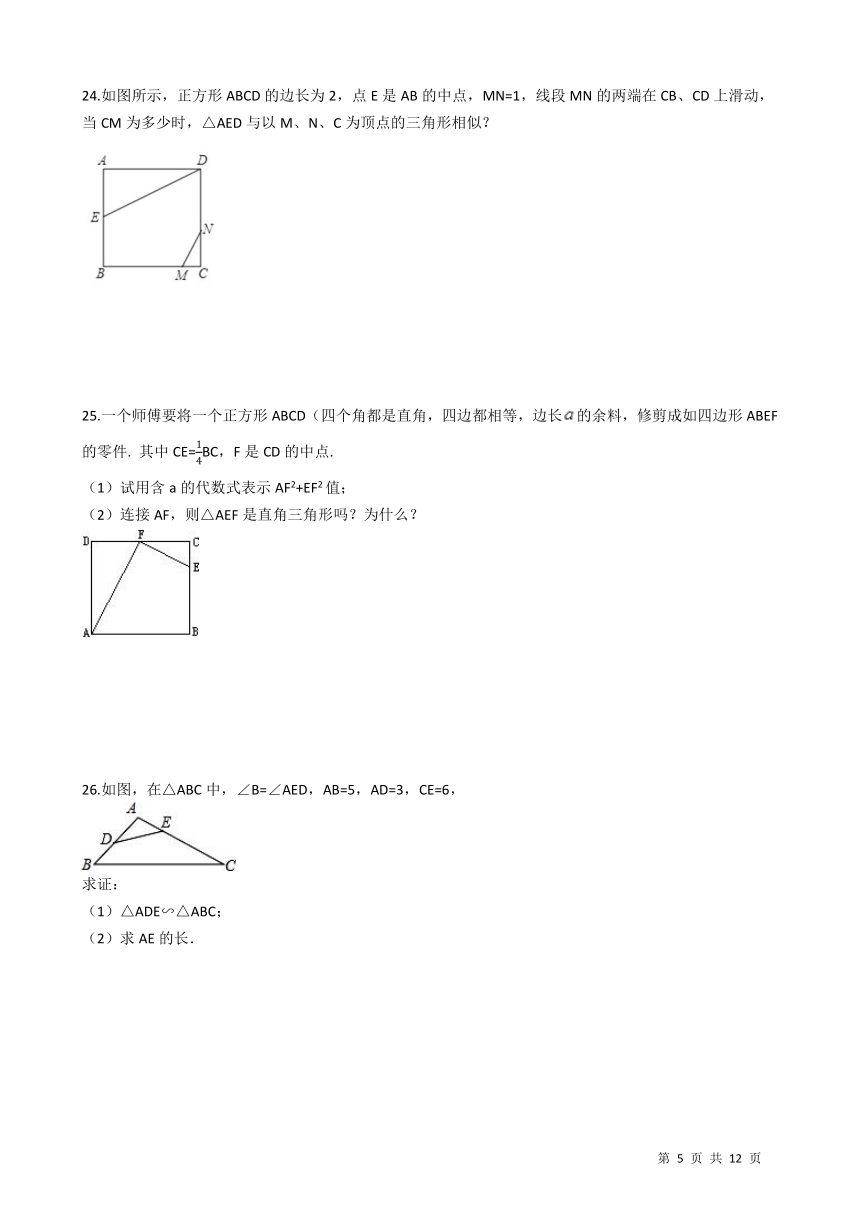
24.如图所示,正方形ABCD的边长为2,点E是AB的中点,MN=1,线段MN的两端在CB、CD上滑动,当CM为多少时,△AED与以M、N、C为顶点的三角形相似? ?/
25.一个师傅要将一个正方形ABCD(四个角都是直角,四边都相等,边长/的余料,修剪成如四边形ABEF的零件. 其中CE=
1
4
BC,F是CD的中点. (1)试用含a的代数式表示AF2+EF2值; (2)连接AF,则△AEF是直角三角形吗?为什么? /
26.如图,在△ABC中,∠B=∠AED,AB=5,AD=3,CE=6, / 求证:
(1)△ADE∽△ABC;
(2)求AE的长.
27.如图,在等腰Rt△ABC中,∠C=90°,正方形DEFG的顶点D在边AC上,点E,F在边AB上,点G在边BC上. / ⑴求证:△ADE≌△BGF; ⑵若正方形DEFG的面积为16,求AC的长.
28.如图1,ABCD为正方形,直线MN分别过AD边与BC边的中点,点P为直线MN上任意一点,连接PB、PC分别与AD边交于E、F两点,PC与BD交于点K,连接AK与PB交于点G. /
(1)探索发现? 当点P落在AD边上时,如图2,试探究PB与AK的位置关系以及PB、PK、AK三者的数量关系(直接写出无需证明);
(2)延伸拓展? 当点P落在正方形外,如图1,以上两个结论是否仍然成立?如果成立请给出证明,如果不成立请说明你的理由;
(3)应用推广? 如图3,在等腰Rt△ABD中,其中∠BAD=90°,腰长为3,M、N分别为AD边与BD边的中点,K为线段DN中点,F为AD边上靠近于D的三等分点.连接KF并延长与直线MN交于点P,连接PB分别与AD、AK交于点E、G.试求四边形EFKG的周长及面积.
答案解析部分
一、单选题
1.【答案】C
2.【答案】B
3.【答案】C
4.【答案】D
5.【答案】B
6.【答案】B
7.【答案】C
8.【答案】D
9.【答案】B
10.【答案】C
二、填空题
11.【答案】2:3
12.【答案】2
13.【答案】9
14.【答案】5
15.【答案】8
16.【答案】
25
4
17.【答案】6
2
或2
10
18.【答案】3
19.【答案】
3
2
20.【答案】①②③④
三、解答题
21.【答案】解:∵DE∥BC,
∴△ADE∽△ABC,
∵DE=2,BC=3,
∴
????
????
=
????
????
=
2
3
22.【答案】解:∵∠C=∠C , ∠A=∠DEC , ∴△DEC∽△BAC , ∴
????
????
=
????
????
, ? 则
????
6
=
5
10
, ? 解得:DE=3.
23.【答案】解:∵ED∥BC,DF∥AB, ∴∠ADE=∠C,∠DFC=∠B, ∴∠AED=∠B, ∴∠AED=∠DFC ∴△ADE∽△DCF
24.【答案】解:∵正方形ABCD的边长为2,点E是AB的中点, ∴∠A=90°,AB=AD=2,AE=
1
2
AB=1, ∴DE=
2
2
+
1
2
=
5
, 分两种情况: ①CM与AE是对应边时,△AED∽△CMN, ∴
????
????
=
????
????
,即
????
1
=
1
5
, 解得:CM=
5
5
; ②CM与AD是对应边时,△AED∽△CNM, ∴
????
????
=
????
????
,即
????
2
=
1
5
, 解得:CM=
2
5
5
. 综上所述:当CM为
5
5
或
2
5
5
时,△AED与以M、N、C为顶点的三角形相似.
25.【答案】解:(1)连接AE,则AB=a,BE=
3
4
a, ∵∠B=90° ∴AE2=
25
16
a2; ∵CE:CF=DF:AD=1:2, ∠C=∠D=90°; ∴△ADF∽△FCE, ∴∠CFE+∠AFD=90° ∴∠AFE=90° ∴AF2+EF2=AE2=
25
16
a2; (2)由(1)中AF2+EF2=AE2 , 可知△AEF是直角三角形。
26.【答案】(1)证明:∵∠B=∠AED,∠A=∠A, ∴△ADE∽△ABC (2)解:由(1)知,△ADE∽△ABC, 则
????
????
=
????
????
, 即
????
????
=
????
????+????
. ∵AB=5,AD=3,CE=6, ∴
3
5
=
????
????+6
, ∴AE=9
27.【答案】(1)证明:∵△ABC是等腰直角三角形,∠C=90°, ∴∠B=∠A=45°, ∵四边形DEFG是正方形, ∴∠BFG=∠AED=90°, 故可得出∠BGF=∠ADE=45°,GF=ED, ∵在△ADE与△BGF中,
∠??????=∠??????
????=????
∠??????=∠??????
, ∴△ADE≌△BGF(ASA); (2)解:过点C作CG⊥AB于点H, / ∵正方形DEFG的面积为16cm2, ∴DE=AE=4cm, ∴AB=3DE=12cm, ∵△ABC是等腰直角三角形,CH⊥AB, ∴AH=
1
2
AB=
1
2
×12=6cm, 在Rt△ADE中, ∵DE=AE=4cm, ∴AD=
??
??
2
+??
??
2
=
4
2
+
4
2
=4
2
cm, ∵CH⊥AB,DE⊥AB, ∴CH∥DE, ∴△ADE∽△ACH, ∴
????
????
=
????
????
,即
4
6
=
4
2
????
, 解得:AC=6
2
cm.
28.【答案】(1)解:PB⊥AK,PB=PK+AK; 理由:如图2中, / ∵点P在MN上,根据对称性易得∠PBC=∠2且PB=PC, 又∠ABK=∠CBK=45°, 在△BKA和△BKC中, {
????=????
∠??????=∠??????
????=????
∴△ABK≌△CBK, ∴∠2=∠3且AK=CK, ∴∠PBC=∠3. 又∠PBC+∠4=90°, ∴∠3+∠4=90°, 即PB⊥AK. ∴PB=PC=PK+CK=PK+AK. (2)以上两个结论仍然成立, 理由如下:如图1中, / ∵点P在MN上,根据对称性易得∠PBC=∠2且PB=PC, 又∠ABK=∠CBK=45°, 在△BKA和△BKC中, {
????=????
∠??????=∠??????
????=????
∴△ABK≌△CBK, ∴∠2=∠3且AK=CK, ∴∠PBC=∠3. 又∠PBC+∠4=90°, ∴∠3+∠4=90°, 即PB⊥AK. ∴PB=PC=PK+CK=PK+AK. (3)如图3中,过点B作AD的平行线交PK延长线与点C,连接CD. / ∵FD∥BD, ∴△FDK∽△CBK. 又DK:BK=1:3, ∴FD:BC=1:3. ∵FD:AD=1:3, ∴BC=AD. ∵BC∥AD且AB⊥AD且AB=AD, ∴四边形ABCD为正方形. ∵PB=PK+AK, 即(PE+BE)=(PF+FK)+AK,又PE=PF, ∴BE=FK+AK. 在Rt△EAB中,∵AE=1,AB=3, ∴BE=
??
??
2
+??
??
2
=
10
. ∵AG⊥BE(上一问结论), ∵Rt△AGE∽Rt△BGA,且相似比为1:3, 设EG=t,AG=3t,BG=9t, ∴BE=10t=
10
, ∴ ??=
10
10
. ∴四边形EFKG的周长=EF+FK+GK+EG=EF+(FK+AK)﹣AG+EG =EF+BE﹣AG+EG=1+10t﹣3t+t=1+8t= 1+
4
5
10
. 过点K作AD垂线,垂足为H, ∵HK∥AB且DK:DB=1:4, ∴KH=
1
4
AB=
3
4
, ∴S四边形EFGH=S△AFK﹣S△AEG=
1
2
?AF?KH﹣
1
2
?AG?EG=
1
2
?2?
3
4
﹣
1
2
?3t?t=
3
5
.
一、单选题(共10题;共30分)
1.如图所示,在△ABC中D为AC边上一点,若∠DBC=∠A , BC=3,AC=6,则CD的长为( )
/
A.?1??????????????????????????????????????????B.?2??????????????????????????????????????????C.?/??????????????????????????????????????????D.?/
2.如图,直线
??
1
∥
??
2
∥
??
3
,直线AC分别交
??
1
,
??
2
,
??
3
于点A,B,C;直线DF分别交
??
1
,
??
2
,
??
3
于点D,E,F.AC与DF相交于点G,且AG=2,GB=1,BC=5,则
????
????
的值为( ??) /
A.?
1
2
??????????????????????????????????????????/B.?
3
5
??????????????????????????????????????????/C.?
2
5
??????????????????????????????????????????/D.?2
3.若两个图形位似,则下列叙述不正确的是(??? )
A.?每对对应点所在的直线相交于同一点??????????????????/B.?两个图形上的对应线段之比等于位似比 C.?两个图形上的对应线段必平行?????????????????????????????/D.?两个图形的面积比等于位似比的平方
4.如图,在△ABC中,点D、E分别在边AB、AC上,下列条件中不能判断△ABC∽△AED的是(? )
/
A.∠AED=∠B B.∠ADE=∠C C.
????
????
=
????
????
D.
????
????
=
????
????
5如图,在平行四边形ABCD中,E为AD的中点,△BCF的面积为4,则△DEF的面积为(???? ) /
A.?1???????????????????????????????????????????/B.?2???????????????????????????????????????????/C.?3???????????????????????????????????????????/D.?4
6.如图,平行四边形ABCD中,E为AD的中点,已知△DEF的面积为S,则四边形ABCE的面积为(?? ) /
A.?8S???????????????????????????????????????/B.?9S???????????????????????????????????????/C.?10S???????????????????????????????????????/D.?11S
7.若两个相似三角形的面积比为4:1,那么这两个三角形的对应边的比为( )
A.?4:1???????????????????????????????????/B.?1:4???????????????????????????????????/C.?2:1???????????????????????????????????/D.?16:1
8.如图,在△ABC中,点D在BC边上,连接AD,点G在线段AD上,GE∥BD,且交AB于点E,GF∥AC,且交CD于点F,则下列结论一定正确的是(??? ). /
A.?
AB
AE
=
AG
AD
??????????????????????/B.?
DF
CF
=
DG
AD
??????????????????????/C.?
FG
AC
=
EG
BD
??????????????????????/D.?
AE
BE
=
CF
DF
9.若2a=3b=4c,且 ??????≠0 ,则
??+??
???2??
的值是( ???)
A.2 B.-2 C.3 D.-3 10.如图,身高1.8m的小超站在某路灯下,发现自己的影长恰好是3m,经测量,此时小超离路灯底部的距离是9m,则路灯离地面的高度是( )
/
A.?5.4m ???/B.?6m ??/C.?7.2m ??/D.?9m
二、填空题(共10题;共32分)
11.已知△ABC∽△DEF? , 且它们的面积之比为4:9,则它们的相似比为________ .
12.如图,如果△ABC与△DEF都是正方形网格中的格点三角形(顶点在格点上),那么S△DEF:S△ABC的值为________. /
13.如图,小明用长为3m的竹竿CD做测量工具,测量学校旗杆AB的高度,移动竹竿,使竹竿与旗杆的顶端C、A与O点在一条直线上,则根据图中数据可得旗杆AB的高为________m. /
14.如图,在△ABC中,∠C=90°,D是AC上一点,DE⊥AB于点E,若AC=8,BC=6,DE=3,则AD的长为 ???????????? .
15.如图,在△ABC中,AD平分∠BAC,与BC边的交点为D,且DC=
1
3
BC,DE∥AC,与AB边的交点为E,若DE=4,则BE的长为________. ?/ ?16.如图,AC∥EF∥DB,若AC=8,BD=12,则EF=________. /
17.矩形纸片ABCD,AB=9,BC=6,在矩形边上有一点P,且DP=3.将矩形纸片折叠,使点B与点P重合,折痕所在直线交矩形两边于点E,F,则EF长为________.
18.如图,在△ABC中,点E,F分别是AC,BC的中点,若S四边形ABFE=9,则S三角形EFC=________. /
19.如图,△ABC中,点D,E分别在边AB,BC上,DE∥AC.若BD=4,DA=2,BE=3,则EC=________. /
20.如图,在四边形ABCD中,AD∥BC,∠BCD=90°,∠ABC=45°,AD=CD,CE平分∠ACB交AB于点E,在BC上截取BF=AE,连接AF交CE于点G,连接DG交AC于点H,过点A作AN⊥BC,垂足为N,AN交CE于点M.则下列结论: ①CM=AF;②CE⊥AF;③△ABF∽△DAH;④GD平分∠AGC, 其中正确的序号是________. /
三、解答题(共8题;共58分)
21.如图,在△ABC中,点D,E分别在边AB,AC上,若DE∥BC,DE=2,BC=3,求
????
????
的值.
/
22.如图,在Rt△ABC中,∠A=90o,AB=6,BC=10,D是AC上一点,CD=5,DE⊥BC于E.求线段DE的长. /
23.如图,在△ABC中,DE ∥BC,DF∥AB,求证:△ADE∽△DCF. /
24.如图所示,正方形ABCD的边长为2,点E是AB的中点,MN=1,线段MN的两端在CB、CD上滑动,当CM为多少时,△AED与以M、N、C为顶点的三角形相似? ?/
25.一个师傅要将一个正方形ABCD(四个角都是直角,四边都相等,边长/的余料,修剪成如四边形ABEF的零件. 其中CE=
1
4
BC,F是CD的中点. (1)试用含a的代数式表示AF2+EF2值; (2)连接AF,则△AEF是直角三角形吗?为什么? /
26.如图,在△ABC中,∠B=∠AED,AB=5,AD=3,CE=6, / 求证:
(1)△ADE∽△ABC;
(2)求AE的长.
27.如图,在等腰Rt△ABC中,∠C=90°,正方形DEFG的顶点D在边AC上,点E,F在边AB上,点G在边BC上. / ⑴求证:△ADE≌△BGF; ⑵若正方形DEFG的面积为16,求AC的长.
28.如图1,ABCD为正方形,直线MN分别过AD边与BC边的中点,点P为直线MN上任意一点,连接PB、PC分别与AD边交于E、F两点,PC与BD交于点K,连接AK与PB交于点G. /
(1)探索发现? 当点P落在AD边上时,如图2,试探究PB与AK的位置关系以及PB、PK、AK三者的数量关系(直接写出无需证明);
(2)延伸拓展? 当点P落在正方形外,如图1,以上两个结论是否仍然成立?如果成立请给出证明,如果不成立请说明你的理由;
(3)应用推广? 如图3,在等腰Rt△ABD中,其中∠BAD=90°,腰长为3,M、N分别为AD边与BD边的中点,K为线段DN中点,F为AD边上靠近于D的三等分点.连接KF并延长与直线MN交于点P,连接PB分别与AD、AK交于点E、G.试求四边形EFKG的周长及面积.
答案解析部分
一、单选题
1.【答案】C
2.【答案】B
3.【答案】C
4.【答案】D
5.【答案】B
6.【答案】B
7.【答案】C
8.【答案】D
9.【答案】B
10.【答案】C
二、填空题
11.【答案】2:3
12.【答案】2
13.【答案】9
14.【答案】5
15.【答案】8
16.【答案】
25
4
17.【答案】6
2
或2
10
18.【答案】3
19.【答案】
3
2
20.【答案】①②③④
三、解答题
21.【答案】解:∵DE∥BC,
∴△ADE∽△ABC,
∵DE=2,BC=3,
∴
????
????
=
????
????
=
2
3
22.【答案】解:∵∠C=∠C , ∠A=∠DEC , ∴△DEC∽△BAC , ∴
????
????
=
????
????
, ? 则
????
6
=
5
10
, ? 解得:DE=3.
23.【答案】解:∵ED∥BC,DF∥AB, ∴∠ADE=∠C,∠DFC=∠B, ∴∠AED=∠B, ∴∠AED=∠DFC ∴△ADE∽△DCF
24.【答案】解:∵正方形ABCD的边长为2,点E是AB的中点, ∴∠A=90°,AB=AD=2,AE=
1
2
AB=1, ∴DE=
2
2
+
1
2
=
5
, 分两种情况: ①CM与AE是对应边时,△AED∽△CMN, ∴
????
????
=
????
????
,即
????
1
=
1
5
, 解得:CM=
5
5
; ②CM与AD是对应边时,△AED∽△CNM, ∴
????
????
=
????
????
,即
????
2
=
1
5
, 解得:CM=
2
5
5
. 综上所述:当CM为
5
5
或
2
5
5
时,△AED与以M、N、C为顶点的三角形相似.
25.【答案】解:(1)连接AE,则AB=a,BE=
3
4
a, ∵∠B=90° ∴AE2=
25
16
a2; ∵CE:CF=DF:AD=1:2, ∠C=∠D=90°; ∴△ADF∽△FCE, ∴∠CFE+∠AFD=90° ∴∠AFE=90° ∴AF2+EF2=AE2=
25
16
a2; (2)由(1)中AF2+EF2=AE2 , 可知△AEF是直角三角形。
26.【答案】(1)证明:∵∠B=∠AED,∠A=∠A, ∴△ADE∽△ABC (2)解:由(1)知,△ADE∽△ABC, 则
????
????
=
????
????
, 即
????
????
=
????
????+????
. ∵AB=5,AD=3,CE=6, ∴
3
5
=
????
????+6
, ∴AE=9
27.【答案】(1)证明:∵△ABC是等腰直角三角形,∠C=90°, ∴∠B=∠A=45°, ∵四边形DEFG是正方形, ∴∠BFG=∠AED=90°, 故可得出∠BGF=∠ADE=45°,GF=ED, ∵在△ADE与△BGF中,
∠??????=∠??????
????=????
∠??????=∠??????
, ∴△ADE≌△BGF(ASA); (2)解:过点C作CG⊥AB于点H, / ∵正方形DEFG的面积为16cm2, ∴DE=AE=4cm, ∴AB=3DE=12cm, ∵△ABC是等腰直角三角形,CH⊥AB, ∴AH=
1
2
AB=
1
2
×12=6cm, 在Rt△ADE中, ∵DE=AE=4cm, ∴AD=
??
??
2
+??
??
2
=
4
2
+
4
2
=4
2
cm, ∵CH⊥AB,DE⊥AB, ∴CH∥DE, ∴△ADE∽△ACH, ∴
????
????
=
????
????
,即
4
6
=
4
2
????
, 解得:AC=6
2
cm.
28.【答案】(1)解:PB⊥AK,PB=PK+AK; 理由:如图2中, / ∵点P在MN上,根据对称性易得∠PBC=∠2且PB=PC, 又∠ABK=∠CBK=45°, 在△BKA和△BKC中, {
????=????
∠??????=∠??????
????=????
∴△ABK≌△CBK, ∴∠2=∠3且AK=CK, ∴∠PBC=∠3. 又∠PBC+∠4=90°, ∴∠3+∠4=90°, 即PB⊥AK. ∴PB=PC=PK+CK=PK+AK. (2)以上两个结论仍然成立, 理由如下:如图1中, / ∵点P在MN上,根据对称性易得∠PBC=∠2且PB=PC, 又∠ABK=∠CBK=45°, 在△BKA和△BKC中, {
????=????
∠??????=∠??????
????=????
∴△ABK≌△CBK, ∴∠2=∠3且AK=CK, ∴∠PBC=∠3. 又∠PBC+∠4=90°, ∴∠3+∠4=90°, 即PB⊥AK. ∴PB=PC=PK+CK=PK+AK. (3)如图3中,过点B作AD的平行线交PK延长线与点C,连接CD. / ∵FD∥BD, ∴△FDK∽△CBK. 又DK:BK=1:3, ∴FD:BC=1:3. ∵FD:AD=1:3, ∴BC=AD. ∵BC∥AD且AB⊥AD且AB=AD, ∴四边形ABCD为正方形. ∵PB=PK+AK, 即(PE+BE)=(PF+FK)+AK,又PE=PF, ∴BE=FK+AK. 在Rt△EAB中,∵AE=1,AB=3, ∴BE=
??
??
2
+??
??
2
=
10
. ∵AG⊥BE(上一问结论), ∵Rt△AGE∽Rt△BGA,且相似比为1:3, 设EG=t,AG=3t,BG=9t, ∴BE=10t=
10
, ∴ ??=
10
10
. ∴四边形EFKG的周长=EF+FK+GK+EG=EF+(FK+AK)﹣AG+EG =EF+BE﹣AG+EG=1+10t﹣3t+t=1+8t= 1+
4
5
10
. 过点K作AD垂线,垂足为H, ∵HK∥AB且DK:DB=1:4, ∴KH=
1
4
AB=
3
4
, ∴S四边形EFGH=S△AFK﹣S△AEG=
1
2
?AF?KH﹣
1
2
?AG?EG=
1
2
?2?
3
4
﹣
1
2
?3t?t=
3
5
.
同课章节目录
- 第1章 反比例函数
- 1.1 反比例函数
- 1.2 反比例函数的图像与性质
- 1.3 反比例函数的应用
- 第2章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程根的判别式
- 2.4 一元二次方程根与系数的关系
- 2.5 一元二次方程的应用
- 第3章 图形的相似
- 3.1 比例线段
- 3.2 平行线分线段成比例
- 3.3 相似图形
- 3.4 相似三角形的判定与性质
- 3.5 相似三角形的应用
- 3.6 位似
- 第4章 锐角三角函数
- 4.1 正弦和余弦
- 4.2 正切
- 4.3 解直角三角形
- 4.4 解直接三角形的应用
- 第5章 用样本推断总体
- 5.1 总体平均数与方差的估计
- 5.2 统计的简单应用
