北师大版必修一第一章1.3.2全集与补集(共29张PPT)
文档属性
| 名称 | 北师大版必修一第一章1.3.2全集与补集(共29张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-01-07 15:56:51 | ||
图片预览






文档简介
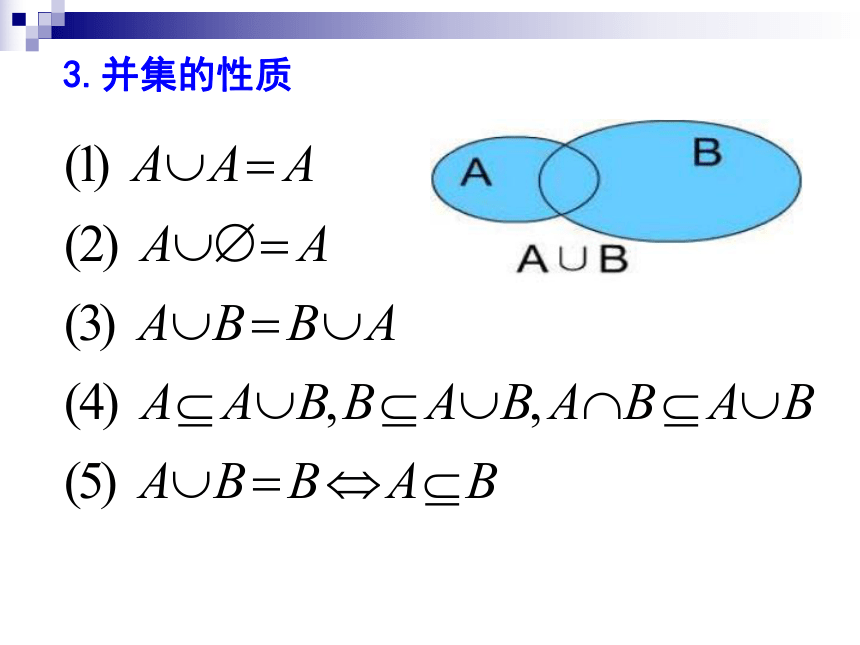
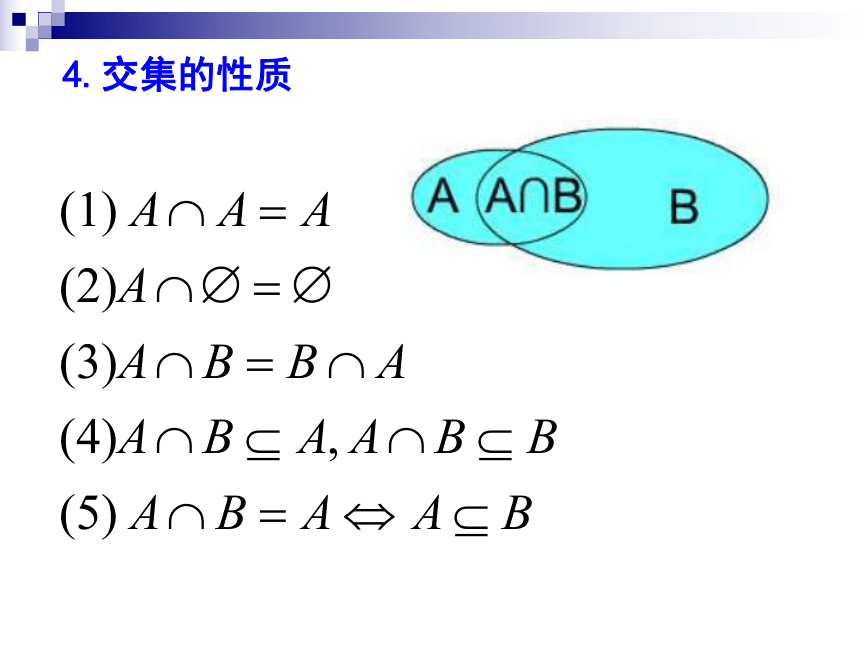
课件29张PPT。并集:A∪B ={x| x ∈ A ,或x ∈ B}A∪BAB2. 交集: A ∩ B ={x| x ∈ A 且x ∈ B}A∩BB复习回顾 3.并集的性质4.交集的性质(1)结合律:(A ∩ B) ∩ C = A ∩ (B ∩ C) = A ∩ B ∩ C5.交集、并集的运算律 (2)结合律:( A U B) U C = A U ( B U C) = A U B U C(3)分配律:A U (B ∩ C) = (A U B) ∩ (A U C) (4)分配律:A ∩ (B U C) = (A ∩ B) U (A ∩ C) JXSDFZ1.3.2全集与补集§3.集合的基本运算1.全集:一般地,如果一个集合含有我们所研究问题中所涉及的所有元素,那么就称这个集合为全集(universe set),通常记作U.2.补集:设U是全集,A是U的一个子集(即 )
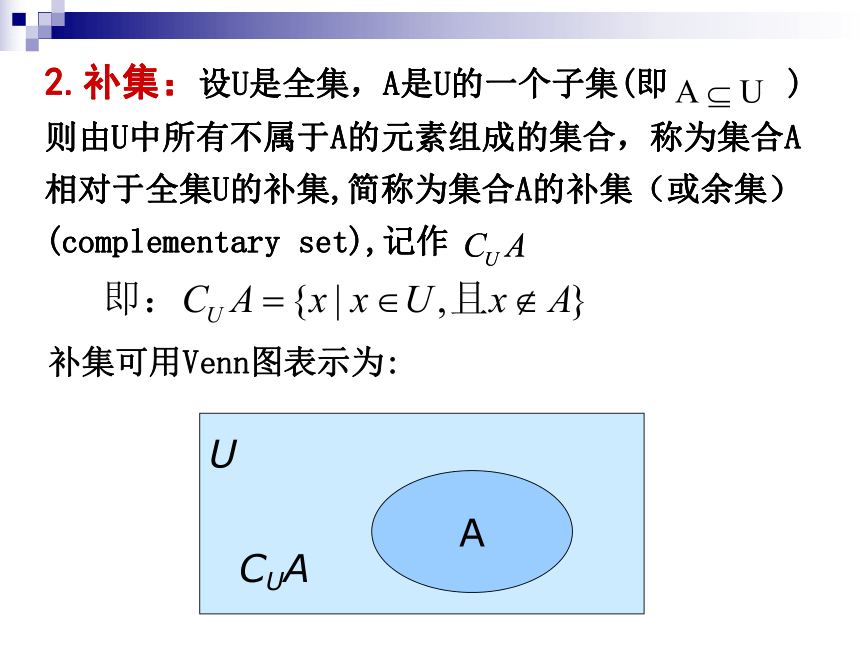
则由U中所有不属于A的元素组成的集合,称为集合A相对于全集U的补集,简称为集合A的补集(或余集)(complementary set),记作 补集可用Venn图表示为:例1.设U={x|x是小于9的正整数},A={1,2,3}
B={3,4,5,6},求CUA,CUB.解:根据题意可知,U={1,2,3,4,5,6,7,8},
所以 CUA={4,5,6,7,8}
CUB={1,2,7,8} .例2. 设全集U={x|x是三角形},A={x|x是锐角三角形},B={x|x是钝角三角形} 求A∩B,CU(A∪B). 若设全集U为全体实数集,A是有理数集,那么U中A的补集就为无理数集,想一想,你是否还能举出身边的例子呢?想一想?3.补集的性质{2}{斜三角形}U1或-3{4,1}解: (1)在数轴上,画出集合A和B(如图)解: (2)A∪B= ∪ =R;解:其中相等有:3.补集的性质例5.试用集合A, B的交集、并集、补集分别表示图中Ⅰ, Ⅱ, Ⅲ, Ⅳ四个部分所表示的集合.1.已知全集U={1,2,3,4,5,6,7},A={2,4,5},
B={1,3,5,7},求A∩(CUB),(CUA)∩ (CUB).解:由题意可知
CUA={1,3,6,7}, CUB={2,4,6},
则A∩(CUB)={2,4},
(CUA)∩ (CUB)={6}.练习一:_________.C练习二:
1.判断正误
(1) 若U={四边形},A={梯形},则CUA={平行四边形}
(2) 若U是全集,且A?B,则CUA?CUB
(3) 若U={1,2,3},A=U,则CUA=?2.设集合A={|2a-1|,2},B={2,3,a2+2a-3},且CBA={5},求实数a的值。3.已知全集U={1,2,3,4,5},非空集合A={x?U|x2-5x+q=0},求CUA及q的值。错错对a=2小 结并集:A∪B ={x| x ∈ A ,或x ∈ B}A∪BAB2. 交集: A ∩ B ={x| x ∈ A 且x ∈ B}A∩BB3.并集的性质4.交集的性质(1)结合律:(A ∩ B) ∩ C = A ∩ (B ∩ C) = A ∩ B ∩ C5.交集、并集的运算律 (2)结合律:( A U B) U C = A U ( B U C) = A U B U C(3)分配律:A U (B ∩ C) = (A U B) ∩ (A U C) (4)分配律:A ∩ (B U C) = (A ∩ B) U (A ∩ C) 7.补集:设U是全集,A是U的一个子集(即 )
则由U中所有不属于A的元素组成的集合,称为集合A相对于全集U的补集,简称为集合A的补集(或余集)(complementary set),记作6.全集:一般地,如果一个集合含有我们所研究问题中所涉及的所有元素,那么就称这个集合为全集(universe set),通常记作U.8.补集的性质课外作业补充再见!作业
课本P12
A组T6, T7,T8
B组T3(提示:对a分类讨论)
则由U中所有不属于A的元素组成的集合,称为集合A相对于全集U的补集,简称为集合A的补集(或余集)(complementary set),记作 补集可用Venn图表示为:例1.设U={x|x是小于9的正整数},A={1,2,3}
B={3,4,5,6},求CUA,CUB.解:根据题意可知,U={1,2,3,4,5,6,7,8},
所以 CUA={4,5,6,7,8}
CUB={1,2,7,8} .例2. 设全集U={x|x是三角形},A={x|x是锐角三角形},B={x|x是钝角三角形} 求A∩B,CU(A∪B). 若设全集U为全体实数集,A是有理数集,那么U中A的补集就为无理数集,想一想,你是否还能举出身边的例子呢?想一想?3.补集的性质{2}{斜三角形}U1或-3{4,1}解: (1)在数轴上,画出集合A和B(如图)解: (2)A∪B= ∪ =R;解:其中相等有:3.补集的性质例5.试用集合A, B的交集、并集、补集分别表示图中Ⅰ, Ⅱ, Ⅲ, Ⅳ四个部分所表示的集合.1.已知全集U={1,2,3,4,5,6,7},A={2,4,5},
B={1,3,5,7},求A∩(CUB),(CUA)∩ (CUB).解:由题意可知
CUA={1,3,6,7}, CUB={2,4,6},
则A∩(CUB)={2,4},
(CUA)∩ (CUB)={6}.练习一:_________.C练习二:
1.判断正误
(1) 若U={四边形},A={梯形},则CUA={平行四边形}
(2) 若U是全集,且A?B,则CUA?CUB
(3) 若U={1,2,3},A=U,则CUA=?2.设集合A={|2a-1|,2},B={2,3,a2+2a-3},且CBA={5},求实数a的值。3.已知全集U={1,2,3,4,5},非空集合A={x?U|x2-5x+q=0},求CUA及q的值。错错对a=2小 结并集:A∪B ={x| x ∈ A ,或x ∈ B}A∪BAB2. 交集: A ∩ B ={x| x ∈ A 且x ∈ B}A∩BB3.并集的性质4.交集的性质(1)结合律:(A ∩ B) ∩ C = A ∩ (B ∩ C) = A ∩ B ∩ C5.交集、并集的运算律 (2)结合律:( A U B) U C = A U ( B U C) = A U B U C(3)分配律:A U (B ∩ C) = (A U B) ∩ (A U C) (4)分配律:A ∩ (B U C) = (A ∩ B) U (A ∩ C) 7.补集:设U是全集,A是U的一个子集(即 )
则由U中所有不属于A的元素组成的集合,称为集合A相对于全集U的补集,简称为集合A的补集(或余集)(complementary set),记作6.全集:一般地,如果一个集合含有我们所研究问题中所涉及的所有元素,那么就称这个集合为全集(universe set),通常记作U.8.补集的性质课外作业补充再见!作业
课本P12
A组T6, T7,T8
B组T3(提示:对a分类讨论)
