北师大版必修一第一章1.3.1交集与并集(共31张PPT)
文档属性
| 名称 | 北师大版必修一第一章1.3.1交集与并集(共31张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-01-07 15:55:34 | ||
图片预览











文档简介
课件31张PPT。1.子集(subset):对于两个集合A与B,如果集合A中的任何一个元素都是集合B中的元素,我们就说集合A包含于集合B,或者说集合B包含集合A。记作A?B,或B?A。这时我们也说A是B的子集。A复习回顾 (1)集合相等:对于集合A与B,如果集合A中的任何一个元素都是集合B中的元素,同时集合B中的任何一个元素都是集合A中的元素,我们就说集合A等于集合B,记作A=B。即:若A?B,且B?A,则A=B。(2)真子集(proper subset):对于集合A与B,如果A?B,且A≠B,我们就说A是B的真子集,记作A?B(或B?A),读作A真包含于B(或B真包含A)。2.子集的两种情形3.子集、真子集的性质:(1)Φ ? A; 若B≠Φ, 则Φ?B(2)A ? A(3)传递性: 若A ?B,B ?C,则A ?C
若A ?B,B ?C,则A ?C4.两点说明:
(1)集合与集合的关系:包含(真包含和相等)
不包含。元素与集合的关系:属于,不属于。作业讲评例3、已知A={x︱x<3},B={x︱x<a}
(1)若B?A,求a的取值范围。
(2)若A?B,求a的取值范围。分析:本题是将不等式的知识与集合的内容联系起来,通过不等式在数轴上的表示即可获解。解:(1)∵ B?A,如右图,
∴a≤3.(2)∵ A?B, 如右图,∴a>3.再分析:由于本题给出的两个相等的集合是有限集,故可根据相等的有限集的性质:
(1)两个集合的所有元素之和相等;
(2)两个集合的所有元素之积相等。
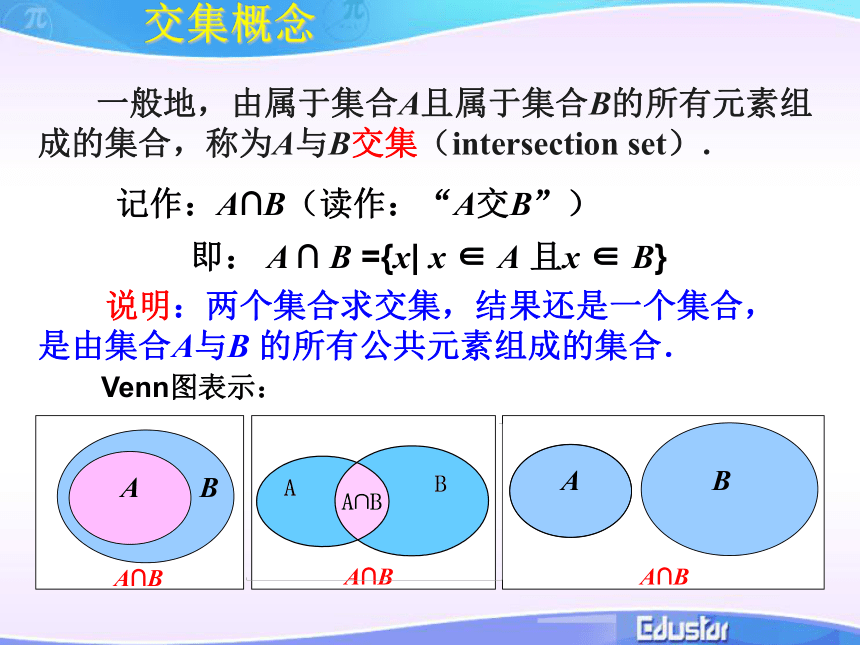
列出关于x,y的方程组,求解即可。JXSDFZ1.3.1并集与交集§3.集合的基本运算思考:类比引入 两个实数除了可以比较大小外,还可以进行四则运算,类比实数的加法运算,两个集合是否也可以“运算”呢? 一般地,由属于集合A且属于集合B的所有元素组成的集合,称为A与B交集(intersection set).记作:A∩B(读作:“A交B”)
即: A ∩ B ={x| x ∈ A 且x ∈ B}Venn图表示: 说明:两个集合求交集,结果还是一个集合,是由集合A与B 的所有公共元素组成的集合.交集概念交集例题2.交集的性质思考:类比引入 求集合的交集是集合间的一种运算,那么,集合间还有其他运算吗?思考:类比引入 考察下列各个集合,你能说出集合C与集合A、B之间的关系吗?(1) A={1,3,5}, B={2,4,6},
C={1,2,3,4,5,6}.(2)A={x|x是有理数}, B={x|x是无理数},C={x|x是实数}. 结论:集合C是由所有属于集合A或属于B的元素组成的. 一般地,由所有属于集合A或属于集合B的元素所组成的集合,称为集合A与B的并集(Union set).记作:A∪B(读作:“A并B”)
即: A∪B ={x| x ∈ A ,或x ∈ B}Venn图表示: 说明:两个集合求并集,结果还是一个集合,是由集合A与B 的所有元素组成的集合(重复元素只看成一个元素).并集概念例2.设A={4,5,6,8},B={3,5,7,8},求AUB.例3.设集合A={x|-1 求AUB.并集例题可以在数轴上表示例3中的并集,如下图:2: 对于A∪B ={x|x∈A或x∈B}。不能认为A∪B是由A的所有元素和B的所有元素所组成的集合,因为A与B可能有公共元素,所以上述看法,从集合的元素互异性看是错误的。4.并集的性质 1.设A={3,5,6,8},B={4,5,7,8}(1)求A∩B,A∪B .
(2)用适当的符号填空:
A∩B___A,B___A∩B,
A∪B ___A,A∪B ___A,
A∩B____A∪B .
课堂练习 5.设A= {x∣x是平行四边形},
B= {x∣x是矩形},求A∩B, A∪B . 4.设A= {x∣x>-2},B= {x∣x≥ 3},
求A∩B, A∪B. 2.设A= {x∣ x<5},B= {x∣x≥0},
求A∩B, A∪B . 3.设A= {x∣x是锐角三角形},
B= {x∣x是钝角三角形},求A∩B, A∪B . (1)结合律:
(A ∩ B) ∩ C = A ∩ (B ∩ C) = A ∩ B ∩ C思考交流5.并集、交集的运算律 (2)结合律:( A U B) U C = A U ( B U C) = A U B U C(3)分配律:
A U (B ∩ C) = (A U B) ∩ (A U C) (4)分配律:
A ∩ (B U C) = (A ∩ B) U (A ∩ C) 小 结并集:A∪B ={x| x ∈ A ,或x ∈ B}A∪BAB2. 交集: A ∩ B ={x| x ∈ A 且x ∈ B}A∩BB3.并集的性质4.交集的性质(1)结合律:(A ∩ B) ∩ C = A ∩ (B ∩ C) = A ∩ B ∩ C5.交集、并集的运算律 (2)结合律:( A U B) U C = A U ( B U C) = A U B U C(3)分配律:A U (B ∩ C) = (A U B) ∩ (A U C) (4)分配律:A ∩ (B U C) = (A ∩ B) U (A ∩ C) 作业
课本P14 A组1,2,(做书上)
A组 3,4 B组1 (做作业本上)再见!作业
课本P12
A组T6, T7,T8
B组T3(提示:对a分类讨论)
若A ?B,B ?C,则A ?C4.两点说明:
(1)集合与集合的关系:包含(真包含和相等)
不包含。元素与集合的关系:属于,不属于。作业讲评例3、已知A={x︱x<3},B={x︱x<a}
(1)若B?A,求a的取值范围。
(2)若A?B,求a的取值范围。分析:本题是将不等式的知识与集合的内容联系起来,通过不等式在数轴上的表示即可获解。解:(1)∵ B?A,如右图,
∴a≤3.(2)∵ A?B, 如右图,∴a>3.再分析:由于本题给出的两个相等的集合是有限集,故可根据相等的有限集的性质:
(1)两个集合的所有元素之和相等;
(2)两个集合的所有元素之积相等。
列出关于x,y的方程组,求解即可。JXSDFZ1.3.1并集与交集§3.集合的基本运算思考:类比引入 两个实数除了可以比较大小外,还可以进行四则运算,类比实数的加法运算,两个集合是否也可以“运算”呢? 一般地,由属于集合A且属于集合B的所有元素组成的集合,称为A与B交集(intersection set).记作:A∩B(读作:“A交B”)
即: A ∩ B ={x| x ∈ A 且x ∈ B}Venn图表示: 说明:两个集合求交集,结果还是一个集合,是由集合A与B 的所有公共元素组成的集合.交集概念交集例题2.交集的性质思考:类比引入 求集合的交集是集合间的一种运算,那么,集合间还有其他运算吗?思考:类比引入 考察下列各个集合,你能说出集合C与集合A、B之间的关系吗?(1) A={1,3,5}, B={2,4,6},
C={1,2,3,4,5,6}.(2)A={x|x是有理数}, B={x|x是无理数},C={x|x是实数}. 结论:集合C是由所有属于集合A或属于B的元素组成的. 一般地,由所有属于集合A或属于集合B的元素所组成的集合,称为集合A与B的并集(Union set).记作:A∪B(读作:“A并B”)
即: A∪B ={x| x ∈ A ,或x ∈ B}Venn图表示: 说明:两个集合求并集,结果还是一个集合,是由集合A与B 的所有元素组成的集合(重复元素只看成一个元素).并集概念例2.设A={4,5,6,8},B={3,5,7,8},求AUB.例3.设集合A={x|-1
(2)用适当的符号填空:
A∩B___A,B___A∩B,
A∪B ___A,A∪B ___A,
A∩B____A∪B .
课堂练习 5.设A= {x∣x是平行四边形},
B= {x∣x是矩形},求A∩B, A∪B . 4.设A= {x∣x>-2},B= {x∣x≥ 3},
求A∩B, A∪B. 2.设A= {x∣ x<5},B= {x∣x≥0},
求A∩B, A∪B . 3.设A= {x∣x是锐角三角形},
B= {x∣x是钝角三角形},求A∩B, A∪B . (1)结合律:
(A ∩ B) ∩ C = A ∩ (B ∩ C) = A ∩ B ∩ C思考交流5.并集、交集的运算律 (2)结合律:( A U B) U C = A U ( B U C) = A U B U C(3)分配律:
A U (B ∩ C) = (A U B) ∩ (A U C) (4)分配律:
A ∩ (B U C) = (A ∩ B) U (A ∩ C) 小 结并集:A∪B ={x| x ∈ A ,或x ∈ B}A∪BAB2. 交集: A ∩ B ={x| x ∈ A 且x ∈ B}A∩BB3.并集的性质4.交集的性质(1)结合律:(A ∩ B) ∩ C = A ∩ (B ∩ C) = A ∩ B ∩ C5.交集、并集的运算律 (2)结合律:( A U B) U C = A U ( B U C) = A U B U C(3)分配律:A U (B ∩ C) = (A U B) ∩ (A U C) (4)分配律:A ∩ (B U C) = (A ∩ B) U (A ∩ C) 作业
课本P14 A组1,2,(做书上)
A组 3,4 B组1 (做作业本上)再见!作业
课本P12
A组T6, T7,T8
B组T3(提示:对a分类讨论)
