沪科版九年级上《第23章解直角三角形》单元评估试卷(有答案)
文档属性
| 名称 | 沪科版九年级上《第23章解直角三角形》单元评估试卷(有答案) |  | |
| 格式 | zip | ||
| 文件大小 | 148.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-01-07 06:33:15 | ||
图片预览




文档简介
沪科版九年级数学上册 第23章解直角三角形 单元评估检测试卷
一、单选题(共10题;共30分)
1.cos30°的值为(?? )
A.?1????????????????????????????????????????/B.?
1
2
????????????????????????????????????????/C.?
3
3
????????????????????????????????????????/D.?
3
2
2.若∠A是锐角,且sinA=
1
2
,则∠A等于(????????)
A.?60°???????????????????????????????????????B.?45°???????????????????????????????????????C.?30°???????????????????????????????????????D.?75°
3.在 ???????????? 中, ∠??=90 °, ∠??=40 °,AB=5,则BC的长为(?? )
A.?5tan40°?????????????????????????????/B.?5cos40°?????????????????????????????/C.?5sin40°?????????????????????????????/D.?
5
cos
40
°
4.在△ABC中,∠C=90°,BC=3,AC=4,则sinA的值是(?? )
A.?
3
4
??????????????????????????????????????????/B.?
3
5
??????????????????????????????????????????/C.?
4
5
??????????????????????????????????????????/D.?
4
3
5.如图,小明要测量河内小岛B到河边公路l的距离,在A点测得∠??????=30°,在C点测得∠??????=60°,又测得AC=50米,则小岛B到公路l的距离为(???)米 /
A.?25????????????????????????????????/B.?25
3
????????????????????????????????/C.?
100
3
3
????????????????????????????????/D.?25+25
3
6.如图,某侦察机在空中A处发现敌方地面目标B,此时从飞机上看目标B的俯角为α,已知飞行高度AC=4500米,tanα=
5
6
, 则飞机到目标B的水平距离BC为( ) /
A.?5400
5
米????????????????????????/B.?5400
3
米????????????????????????/C.?5600
5
米????????????????????????/D.?5600
3
米
7.(2017?南宁)如图,一艘海轮位于灯塔P的南偏东45°方向,距离灯塔60n mile的A处,它沿正北方向航行一段时间后,到达位于灯塔P的北偏东30°方向上的B处,这时,B处与灯塔P的距离为(?? ) /
A.?60
3
?n mile????????????????/B.?60
2
?n mile????????????????/C.?30
3
?n mile????????????????/D.?30
2
?n mile
8.某轮船由西向东航行,在A处测得小岛P的方位是北偏东75°,继续航行7海里后,在B处测得小岛P的方位是北偏东60°,则此时轮船与小岛P的距离BP=( ) /
A.?7海里????????????????????????????????/B.?14海里????????????????????????????????/C.?3.5海里?????????????????????????????????/D.?4海里
9.如图,在梯形ABCD中,∠ABC=90o,AE∥CD交BC于E,O是AC的中点,AB=
3
,AD=2,BC=3,下列结论:①∠CAE=30o;②AC=2AB;③S△ADC=2S△ABE;④BO⊥CD,其中正确的是(?????) /
A.?①②③???????????????????????????????/B.?②③④???????????????????????????????/C.?①③④???????????????????????????????/D.?①②③④
10.(2017?杭州)如图,在△ABC中,AB=AC,BC=12,E为AC边的中点,线段BE的垂直平分线交边BC于点D.设BD=x,tan∠ACB=y,则(?? ) /
A.?x﹣y2=3?????????????????????????B.?2x﹣y2=9?????????????????????????C.?3x﹣y2=15?????????????????????????D.?4x﹣y2=21
二、填空题(共10题;共30分)
11.在Rt△ABC中,∠C=90°,AB=2,BC=
3
,则sin
??
2
?=________
12.如图,∠AOB=45°,点M,N在边OA上,OM=3,ON=7,点P是直线OB上的点,要使点P,M,N构成等腰三角形的点P有________个.
/
13.如图,某地修建高速公路,要从B地向C地修一座隧道(B、C在同一水平面上),为了测量B、C两地之间的距离,某工程队乘坐热气球从C地出发垂直上升100m到达A处,在A处观察B地的俯角为30°,则BC两地间的距离为________?m. /
14.某轮船由西向东航行,在A处测得小岛P的方位是北偏东75°,又继续航行7海里后,在B处测得小岛P的方位是北偏东60°,则此时轮船与小岛P的距离BP=________海里.
/
15.如图,四边形ABCd为边长是2的正方形,△BPC为等边三角形,连接PD、BD,则△BDP的面积是________. /
16.如图,△ABC是等边三角形,点D是BC边上任意一点,DE⊥AB于点E,DF⊥AC于点F.若BC=2,则DE+DF=________.
17.在△ABC中,∠B=45°,cosA=
1
2
,则∠C的度数是________.
18.如图,一艘海轮位于灯塔P的东北方向,距离灯塔 40
2
海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东30°方向上的B处,则海轮行驶的路程AB为________海里(结果保留根号).
/
19.如图所示,某拦水大坝的横断面为梯形ABCD,AE、DF为梯形的高,其中迎水坡AB的坡角α=45°,坡长AB= 6
2
米,背水坡CD的坡度i=1:
3
(i为DF与FC的比值),则背水坡CD的坡长为________米. /
20.如图,港口A在观测站O的正东方向,OA=4km , 某船从港口A出发,沿北偏东15°方向航行一段距离后到达B处,此时从观测站O处测得该船位于北偏东60°的方向,则该船航行的距离(即AB的长)为________km . /?
三、解答题(共8题;共60分)
21.计算: |?1|?
1
2
8
?
(5???)
°
+4cos45° .
22.如图,从热气球C处测得地面A,B两点的俯角分别为 30° , 45° ,此时热气球C处所在位置到地面上点A的距离为400米.求地面上A,B两点间的距离. /
23.甲、乙两船同时从港口A出发,甲船以12海里/时的速度向 北偏东35°航行,乙船向南偏东55°航行,2小时后,甲船到达C岛,乙船到达B岛,若C、B两船相距30海里,问乙船的速度是每小时多少海里? /
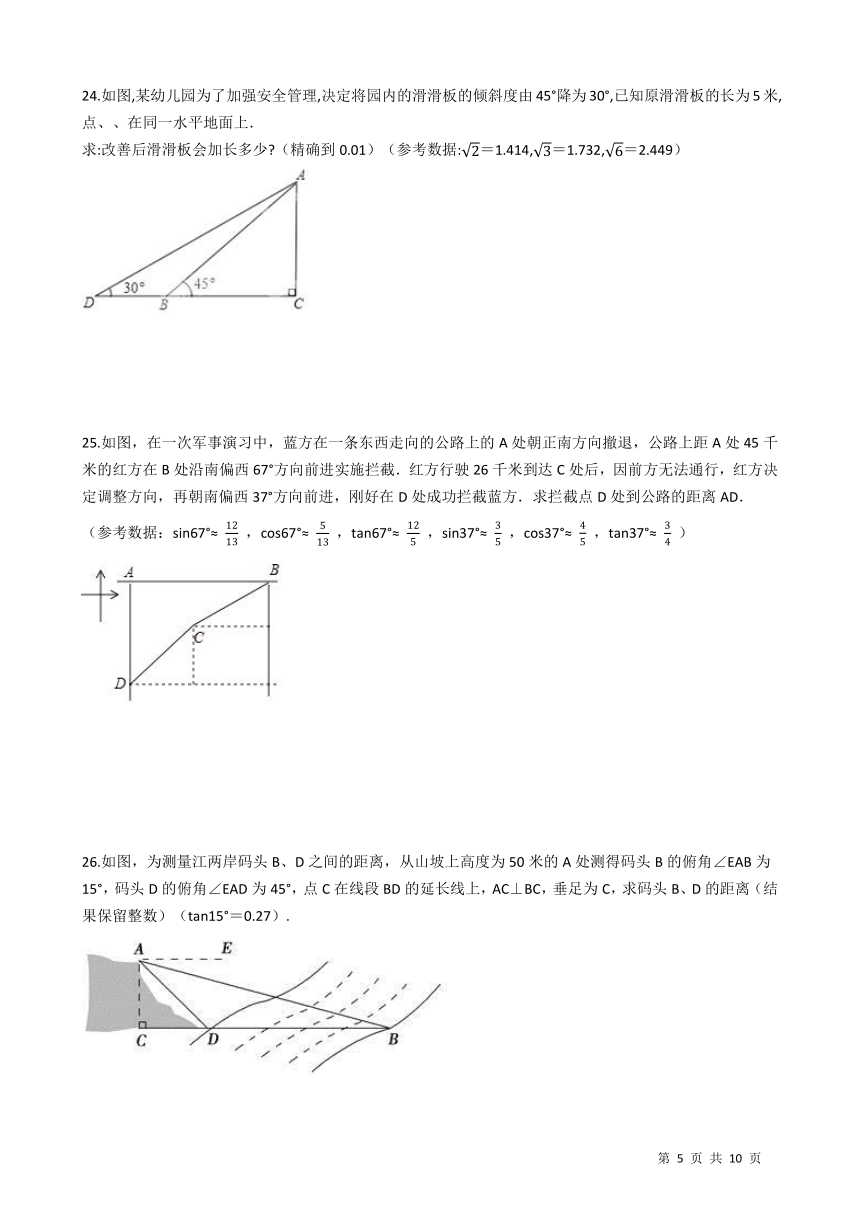
24.如图,某幼儿园为了加强安全管理,决定将园内的滑滑板的倾斜度由45°降为30°,已知原滑滑板的长为5米,点、、在同一水平地面上. 求:改善后滑滑板会加长多少?(精确到0.01)(参考数据:
2
=1.414,
3
=1.732,
6
=2.449)
/
25.如图,在一次军事演习中,蓝方在一条东西走向的公路上的A处朝正南方向撤退,公路上距A处45千米的红方在B处沿南偏西67°方向前进实施拦截.红方行驶26千米到达C处后,因前方无法通行,红方决定调整方向,再朝南偏西37°方向前进,刚好在D处成功拦截蓝方.求拦截点D处到公路的距离AD. (参考数据:sin67°≈
12
13
,cos67°≈
5
13
,tan67°≈
12
5
,sin37°≈
3
5
,cos37°≈
4
5
,tan37°≈
3
4
) /
26.如图,为测量江两岸码头B、D之间的距离,从山坡上高度为50米的A处测得码头B的俯角∠EAB为15°,码头D的俯角∠EAD为45°,点C在线段BD的延长线上,AC⊥BC,垂足为C,求码头B、D的距离(结果保留整数)(tan15°=0.27). /
27.如图,某校一幢教学大楼的顶部竖有一块“传承文明,启智求真”的宣传牌CD、小明在山坡的坡脚A处测得宣传牌底部D的仰角为60°,沿山坡向上走到B处测得宣传牌顶部C的仰角为45°.已知山坡AB的坡度i=1:
3
, AB=10米,AE=15米,求这块宣传牌CD的高度.(测角器的高度忽略不计,结果精确到0.1米.参考数据:
2
≈1.414,
3
≈1.732)
?/
28.如图,小俊在A处利用高为1.5米的测角仪AB测得楼EF顶部E的仰角为30°,然后前进12米到达C处,又测得楼顶E的仰角为60°,求楼EF的高度.(结果精确到0.1米) /
答案解析部分
一、单选题
1.【答案】D
2.【答案】C
3.【答案】B
4.【答案】B
5.【答案】B
6.【答案】A
7.【答案】B
8.【答案】A
9.【答案】D
10.【答案】B
二、填空题
11.【答案】
1
2
12.【答案】3
13.【答案】100
3
14.【答案】7
15.【答案】4
3
﹣4
16.【答案】
3
17.【答案】75°
18.【答案】40+40
3
19.【答案】12
20.【答案】2 /?
三、解答题
21.【答案】解: |?1|?
1
2
8
?
(5???)
°
+4cos45° , = 1?
1
2
×2
2
?1+4×
2
2
, =
2
.
22.【答案】解: 过点C作 ????⊥???? 于点D / 由题意得 ∠??=∠??????=30° , ∠??=∠??????=45° ∵在Rt△ACD中, sin??=
????
????
, cos??=
????
????
∴CD=AC sin?? = 400sin30° =400×
1
2
=200(m)? AD= AC cos?? = 400cos30° =400×
3
2
=200
3
(m) ∵在Rt△BCD中, tanB=
????
????
∴BD=
????
tan??
=
200
tan45°
=200 (m) ∴AB=AD+BD= (200
3
+200) m 答:地面上A,B两点间的距离为 (200
3
+200) m .
23.【答案】解:根据题意得:AC=12×2=24,BC=30,∠BAC=90°. ∴AC2+AB2=BC2 . ∴AB2=BC2-AC2=302-242=324 ∴AB=18. ∴乙船的航速是:18÷2=9海里/时.
24.【答案】解:在Rt△ABC中, ∵AB=5,∠ABC=45°, ∴AC=ABsin45°=5×
2
2
=
5
2
2
, 在Rt△ADC中,∠ADC=30°, ∴AD=
????
sin30°
=5
2
=5×1.414=7.07, AD﹣AB=7.07﹣5=2.07(米). 答:改善后滑滑板约会加长2.07米.
25.【答案】解:在Rt△BCF中, / BF=BC×cos∠FBC≈10, CF=BC×sin∠FBC≈24, ∴DE=45﹣24=21, 在Rt△DCE中,CE=
????
??????∠??????
≈28, ∴AD=BG=BF+CE≈38. 答:点D处到公路的距离AD约为38千米.
26.【答案】解:∵AE∥BC,∴∠ADC=∠EAD=45°. 又∵AC⊥CD,∴CD=AC=50. ∵AE∥BC, ∴∠ABC=∠EAB=15°. 又∵tan∠ABC=
????
????
, ∴BC=
????
tan15°
≈185.2. ∴BD=185.2-50≈135(米).
27.【答案】解:过B作BF⊥AE,交EA的延长线于F,作BG⊥DE于G.
Rt△ABF中,i=tan∠BAF=
1
3
=
3
3
,
∴∠BAF=30°,
∴BF=
1
2
AB=5,AF=5
3
.
∴BG=AF+AE=5
3
+15.
Rt△BGC中,∠CBG=45°,
∴CG=BG=5
3
+15.
Rt△ADE中,∠DAE=60°,AE=15,
∴DE=
3
AE=15
3
.
∴CD=CG+GE﹣DE=5
3
+15+5﹣15
3
=20﹣10
3
≈2.7m.
答:宣传牌CD高约2.7米.
/
28.【答案】解:设楼EF的高为x米,可得EG=EF﹣GF=(x﹣1.5)米, 依题意得:EF⊥AF,DC⊥AF,BA⊥AF,BD⊥EF(设垂足为G), 在Rt△EGD中,DG=
????
tan∠??????
=
3
3
(x﹣1.5)米,在Rt△EGB中,BG=
3
(x﹣1.5)米, ∴CA=DB=BG﹣DG=
2
3
3
(x﹣1.5)米, ∵CA=12米,∴
2
3
3
(x﹣1.5)=12, 解得:x=6
3
+1.5≈11.9, 则楼EF的高度约为11.9米.
一、单选题(共10题;共30分)
1.cos30°的值为(?? )
A.?1????????????????????????????????????????/B.?
1
2
????????????????????????????????????????/C.?
3
3
????????????????????????????????????????/D.?
3
2
2.若∠A是锐角,且sinA=
1
2
,则∠A等于(????????)
A.?60°???????????????????????????????????????B.?45°???????????????????????????????????????C.?30°???????????????????????????????????????D.?75°
3.在 ???????????? 中, ∠??=90 °, ∠??=40 °,AB=5,则BC的长为(?? )
A.?5tan40°?????????????????????????????/B.?5cos40°?????????????????????????????/C.?5sin40°?????????????????????????????/D.?
5
cos
40
°
4.在△ABC中,∠C=90°,BC=3,AC=4,则sinA的值是(?? )
A.?
3
4
??????????????????????????????????????????/B.?
3
5
??????????????????????????????????????????/C.?
4
5
??????????????????????????????????????????/D.?
4
3
5.如图,小明要测量河内小岛B到河边公路l的距离,在A点测得∠??????=30°,在C点测得∠??????=60°,又测得AC=50米,则小岛B到公路l的距离为(???)米 /
A.?25????????????????????????????????/B.?25
3
????????????????????????????????/C.?
100
3
3
????????????????????????????????/D.?25+25
3
6.如图,某侦察机在空中A处发现敌方地面目标B,此时从飞机上看目标B的俯角为α,已知飞行高度AC=4500米,tanα=
5
6
, 则飞机到目标B的水平距离BC为( ) /
A.?5400
5
米????????????????????????/B.?5400
3
米????????????????????????/C.?5600
5
米????????????????????????/D.?5600
3
米
7.(2017?南宁)如图,一艘海轮位于灯塔P的南偏东45°方向,距离灯塔60n mile的A处,它沿正北方向航行一段时间后,到达位于灯塔P的北偏东30°方向上的B处,这时,B处与灯塔P的距离为(?? ) /
A.?60
3
?n mile????????????????/B.?60
2
?n mile????????????????/C.?30
3
?n mile????????????????/D.?30
2
?n mile
8.某轮船由西向东航行,在A处测得小岛P的方位是北偏东75°,继续航行7海里后,在B处测得小岛P的方位是北偏东60°,则此时轮船与小岛P的距离BP=( ) /
A.?7海里????????????????????????????????/B.?14海里????????????????????????????????/C.?3.5海里?????????????????????????????????/D.?4海里
9.如图,在梯形ABCD中,∠ABC=90o,AE∥CD交BC于E,O是AC的中点,AB=
3
,AD=2,BC=3,下列结论:①∠CAE=30o;②AC=2AB;③S△ADC=2S△ABE;④BO⊥CD,其中正确的是(?????) /
A.?①②③???????????????????????????????/B.?②③④???????????????????????????????/C.?①③④???????????????????????????????/D.?①②③④
10.(2017?杭州)如图,在△ABC中,AB=AC,BC=12,E为AC边的中点,线段BE的垂直平分线交边BC于点D.设BD=x,tan∠ACB=y,则(?? ) /
A.?x﹣y2=3?????????????????????????B.?2x﹣y2=9?????????????????????????C.?3x﹣y2=15?????????????????????????D.?4x﹣y2=21
二、填空题(共10题;共30分)
11.在Rt△ABC中,∠C=90°,AB=2,BC=
3
,则sin
??
2
?=________
12.如图,∠AOB=45°,点M,N在边OA上,OM=3,ON=7,点P是直线OB上的点,要使点P,M,N构成等腰三角形的点P有________个.
/
13.如图,某地修建高速公路,要从B地向C地修一座隧道(B、C在同一水平面上),为了测量B、C两地之间的距离,某工程队乘坐热气球从C地出发垂直上升100m到达A处,在A处观察B地的俯角为30°,则BC两地间的距离为________?m. /
14.某轮船由西向东航行,在A处测得小岛P的方位是北偏东75°,又继续航行7海里后,在B处测得小岛P的方位是北偏东60°,则此时轮船与小岛P的距离BP=________海里.
/
15.如图,四边形ABCd为边长是2的正方形,△BPC为等边三角形,连接PD、BD,则△BDP的面积是________. /
16.如图,△ABC是等边三角形,点D是BC边上任意一点,DE⊥AB于点E,DF⊥AC于点F.若BC=2,则DE+DF=________.
17.在△ABC中,∠B=45°,cosA=
1
2
,则∠C的度数是________.
18.如图,一艘海轮位于灯塔P的东北方向,距离灯塔 40
2
海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东30°方向上的B处,则海轮行驶的路程AB为________海里(结果保留根号).
/
19.如图所示,某拦水大坝的横断面为梯形ABCD,AE、DF为梯形的高,其中迎水坡AB的坡角α=45°,坡长AB= 6
2
米,背水坡CD的坡度i=1:
3
(i为DF与FC的比值),则背水坡CD的坡长为________米. /
20.如图,港口A在观测站O的正东方向,OA=4km , 某船从港口A出发,沿北偏东15°方向航行一段距离后到达B处,此时从观测站O处测得该船位于北偏东60°的方向,则该船航行的距离(即AB的长)为________km . /?
三、解答题(共8题;共60分)
21.计算: |?1|?
1
2
8
?
(5???)
°
+4cos45° .
22.如图,从热气球C处测得地面A,B两点的俯角分别为 30° , 45° ,此时热气球C处所在位置到地面上点A的距离为400米.求地面上A,B两点间的距离. /
23.甲、乙两船同时从港口A出发,甲船以12海里/时的速度向 北偏东35°航行,乙船向南偏东55°航行,2小时后,甲船到达C岛,乙船到达B岛,若C、B两船相距30海里,问乙船的速度是每小时多少海里? /
24.如图,某幼儿园为了加强安全管理,决定将园内的滑滑板的倾斜度由45°降为30°,已知原滑滑板的长为5米,点、、在同一水平地面上. 求:改善后滑滑板会加长多少?(精确到0.01)(参考数据:
2
=1.414,
3
=1.732,
6
=2.449)
/
25.如图,在一次军事演习中,蓝方在一条东西走向的公路上的A处朝正南方向撤退,公路上距A处45千米的红方在B处沿南偏西67°方向前进实施拦截.红方行驶26千米到达C处后,因前方无法通行,红方决定调整方向,再朝南偏西37°方向前进,刚好在D处成功拦截蓝方.求拦截点D处到公路的距离AD. (参考数据:sin67°≈
12
13
,cos67°≈
5
13
,tan67°≈
12
5
,sin37°≈
3
5
,cos37°≈
4
5
,tan37°≈
3
4
) /
26.如图,为测量江两岸码头B、D之间的距离,从山坡上高度为50米的A处测得码头B的俯角∠EAB为15°,码头D的俯角∠EAD为45°,点C在线段BD的延长线上,AC⊥BC,垂足为C,求码头B、D的距离(结果保留整数)(tan15°=0.27). /
27.如图,某校一幢教学大楼的顶部竖有一块“传承文明,启智求真”的宣传牌CD、小明在山坡的坡脚A处测得宣传牌底部D的仰角为60°,沿山坡向上走到B处测得宣传牌顶部C的仰角为45°.已知山坡AB的坡度i=1:
3
, AB=10米,AE=15米,求这块宣传牌CD的高度.(测角器的高度忽略不计,结果精确到0.1米.参考数据:
2
≈1.414,
3
≈1.732)
?/
28.如图,小俊在A处利用高为1.5米的测角仪AB测得楼EF顶部E的仰角为30°,然后前进12米到达C处,又测得楼顶E的仰角为60°,求楼EF的高度.(结果精确到0.1米) /
答案解析部分
一、单选题
1.【答案】D
2.【答案】C
3.【答案】B
4.【答案】B
5.【答案】B
6.【答案】A
7.【答案】B
8.【答案】A
9.【答案】D
10.【答案】B
二、填空题
11.【答案】
1
2
12.【答案】3
13.【答案】100
3
14.【答案】7
15.【答案】4
3
﹣4
16.【答案】
3
17.【答案】75°
18.【答案】40+40
3
19.【答案】12
20.【答案】2 /?
三、解答题
21.【答案】解: |?1|?
1
2
8
?
(5???)
°
+4cos45° , = 1?
1
2
×2
2
?1+4×
2
2
, =
2
.
22.【答案】解: 过点C作 ????⊥???? 于点D / 由题意得 ∠??=∠??????=30° , ∠??=∠??????=45° ∵在Rt△ACD中, sin??=
????
????
, cos??=
????
????
∴CD=AC sin?? = 400sin30° =400×
1
2
=200(m)? AD= AC cos?? = 400cos30° =400×
3
2
=200
3
(m) ∵在Rt△BCD中, tanB=
????
????
∴BD=
????
tan??
=
200
tan45°
=200 (m) ∴AB=AD+BD= (200
3
+200) m 答:地面上A,B两点间的距离为 (200
3
+200) m .
23.【答案】解:根据题意得:AC=12×2=24,BC=30,∠BAC=90°. ∴AC2+AB2=BC2 . ∴AB2=BC2-AC2=302-242=324 ∴AB=18. ∴乙船的航速是:18÷2=9海里/时.
24.【答案】解:在Rt△ABC中, ∵AB=5,∠ABC=45°, ∴AC=ABsin45°=5×
2
2
=
5
2
2
, 在Rt△ADC中,∠ADC=30°, ∴AD=
????
sin30°
=5
2
=5×1.414=7.07, AD﹣AB=7.07﹣5=2.07(米). 答:改善后滑滑板约会加长2.07米.
25.【答案】解:在Rt△BCF中, / BF=BC×cos∠FBC≈10, CF=BC×sin∠FBC≈24, ∴DE=45﹣24=21, 在Rt△DCE中,CE=
????
??????∠??????
≈28, ∴AD=BG=BF+CE≈38. 答:点D处到公路的距离AD约为38千米.
26.【答案】解:∵AE∥BC,∴∠ADC=∠EAD=45°. 又∵AC⊥CD,∴CD=AC=50. ∵AE∥BC, ∴∠ABC=∠EAB=15°. 又∵tan∠ABC=
????
????
, ∴BC=
????
tan15°
≈185.2. ∴BD=185.2-50≈135(米).
27.【答案】解:过B作BF⊥AE,交EA的延长线于F,作BG⊥DE于G.
Rt△ABF中,i=tan∠BAF=
1
3
=
3
3
,
∴∠BAF=30°,
∴BF=
1
2
AB=5,AF=5
3
.
∴BG=AF+AE=5
3
+15.
Rt△BGC中,∠CBG=45°,
∴CG=BG=5
3
+15.
Rt△ADE中,∠DAE=60°,AE=15,
∴DE=
3
AE=15
3
.
∴CD=CG+GE﹣DE=5
3
+15+5﹣15
3
=20﹣10
3
≈2.7m.
答:宣传牌CD高约2.7米.
/
28.【答案】解:设楼EF的高为x米,可得EG=EF﹣GF=(x﹣1.5)米, 依题意得:EF⊥AF,DC⊥AF,BA⊥AF,BD⊥EF(设垂足为G), 在Rt△EGD中,DG=
????
tan∠??????
=
3
3
(x﹣1.5)米,在Rt△EGB中,BG=
3
(x﹣1.5)米, ∴CA=DB=BG﹣DG=
2
3
3
(x﹣1.5)米, ∵CA=12米,∴
2
3
3
(x﹣1.5)=12, 解得:x=6
3
+1.5≈11.9, 则楼EF的高度约为11.9米.
