湘教版九年级下《第三章投影与视图》单元评估检测试卷(有答案)
文档属性
| 名称 | 湘教版九年级下《第三章投影与视图》单元评估检测试卷(有答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 223.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-01-07 00:00:00 | ||
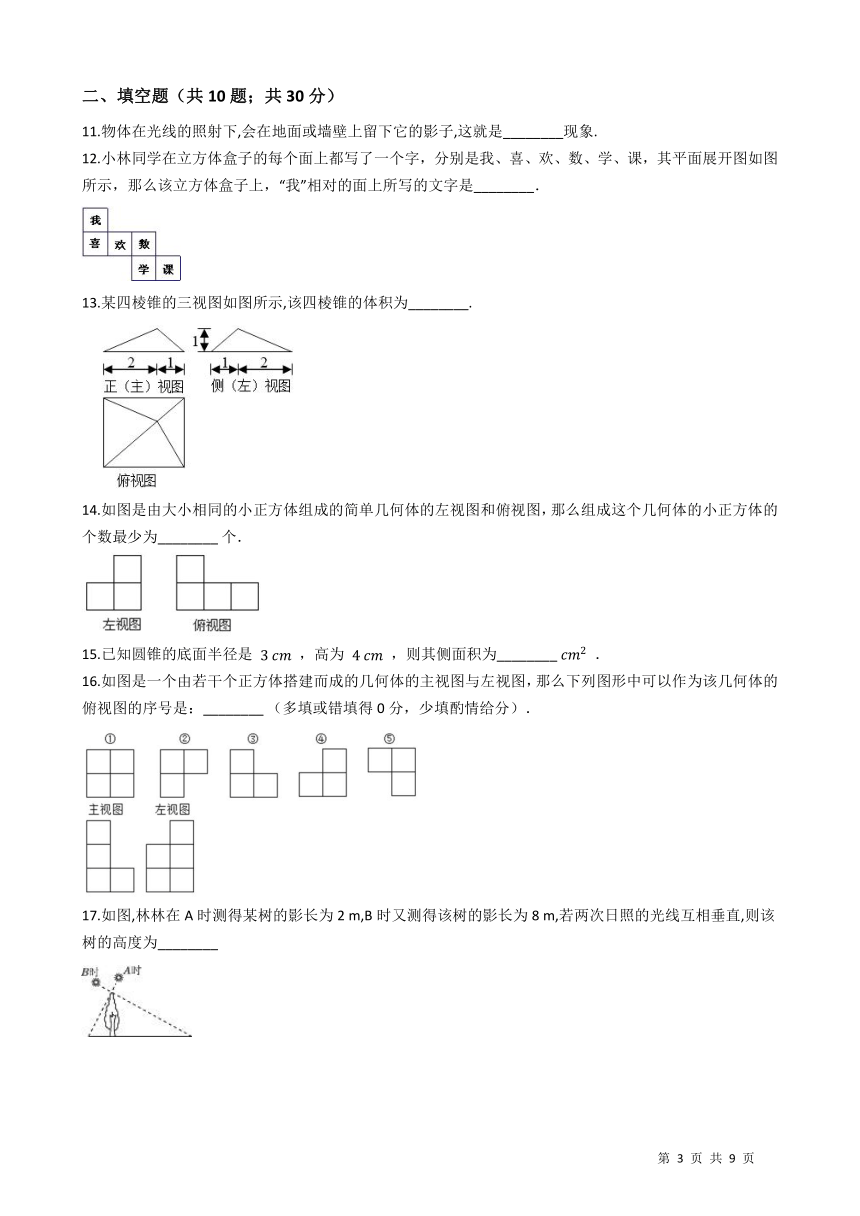
图片预览


文档简介
湘教版九年级数学下册 第三章 投影与视图 单元评估检测试卷
一、单选题(共10题;共30分)
1.由7个大小相同的正方体搭成的几何体如图所示,则以下结论:①主视图既是轴对称图形,又是中心对称图形;??? ②俯视图是中心对称图形;③左视图不是中心对称图形;④俯视图和左视图都不是轴对称图形其中正确结论是(??? ) /
A.?①③?????????????????????????????????????B.?①④?????????????????????????????????????C.?②③?????????????????????????????????????D.?②④
2.下列立体图形中,主视图是三角形的是(??? )。
A./B/C/D/
3.一个几何体的三视图如图所示,该几何体是(??? )/
A.?直三棱柱????????????????????????????????/B.?长方体????????????????????????????????/C.?圆锥????????????????????????????????/D.?立方体
4.如图,是由一个圆柱体和一个长方体组成的几何体.其主视图是( ) /
A.?/????????????????/B.?/????????????????/C.?/????????????????/D.?/
5.如图是一个正方体的表面展开图,如果相对面上所标的两个数互为相反数,那么图中x的值是( ) /
A.?8???????????????????????????????????????????/B.?3???????????????????????????????????????????/C.?2???????????????????????????????????????????/D.?-3
6.如图是正方体的展开图,则正方体相对两个面上的数字之和的最小值是 ( ??). /
A.?4???????????????????????????????????????????/B.?6???????????????????????????????????????????/C.?7???????????????????????????????????????????/D.?8
7.如图,D,E,F分别是等边△ABC的边AB,BC,CA的中点,现沿着虚线折起,使A,B,C三点重合,折起后得到的空间图形是(???) /
A.?棱锥????????????????????????????????????B.?圆锥????????????????????????????????????C.?棱柱????????????????????????????????????D.?正方体
8.某几何体的三视图如图所示,则这个几何体是(?? ) /
A.?圆柱?????????????????????????????????????B.?正方体?????????????????????????????????????C.?球?????????????????????????????????????D.?圆锥
9.下图是由八个相同的小正方体组合而成的几何体,其俯视图是(? ????)
/
A.?/??????????????????/B.?/??????????????????/C.?/??????????????????/D.?/
10.如图是一个切去了一个角的正方体纸盒,切面与棱的交点A,B,C均是棱的中点,现将纸盒剪开展成平面,则展开图不可能是( ) /?
A.?/??????????????????/B.?/??????????????????/C.?/??????????????????/D.?/?
二、填空题(共10题;共30分)
11.物体在光线的照射下,会在地面或墙壁上留下它的影子,这就是________现象.
12.小林同学在立方体盒子的每个面上都写了一个字,分别是我、喜、欢、数、学、课,其平面展开图如图所示,那么该立方体盒子上,“我”相对的面上所写的文字是________. /
13.某四棱锥的三视图如图所示,该四棱锥的体积为________. /
14.如图是由大小相同的小正方体组成的简单几何体的左视图和俯视图,那么组成这个几何体的小正方体的个数最少为________?个. /
15.已知圆锥的底面半径是 3????? ,高为 4????? ,则其侧面积为________ ??
??
2
.
16.如图是一个由若干个正方体搭建而成的几何体的主视图与左视图,那么下列图形中可以作为该几何体的俯视图的序号是:________?(多填或错填得0分,少填酌情给分). /
17.如图,林林在A时测得某树的影长为2 m,B时又测得该树的影长为8 m,若两次日照的光线互相垂直,则该树的高度为________? /
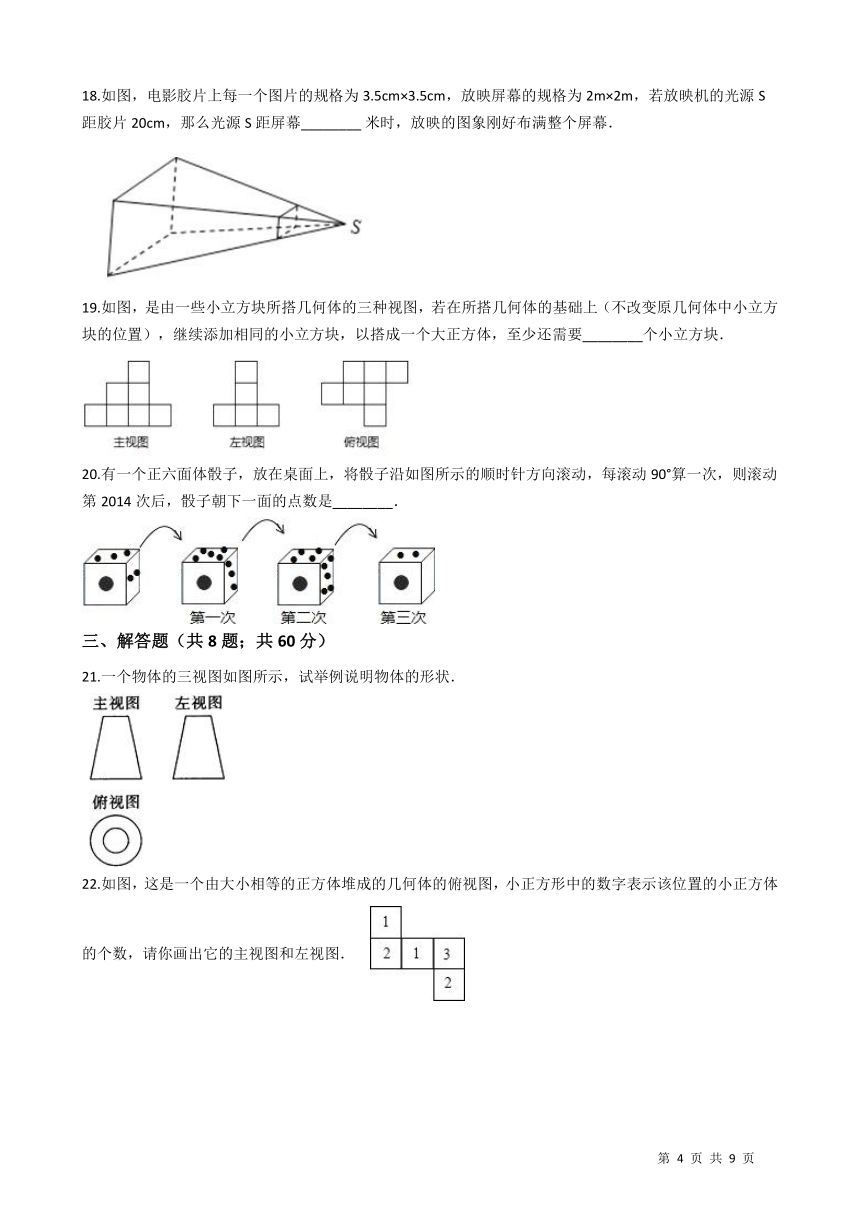
18.如图,电影胶片上每一个图片的规格为3.5cm×3.5cm,放映屏幕的规格为2m×2m,若放映机的光源S距胶片20cm,那么光源S距屏幕________?米时,放映的图象刚好布满整个屏幕. /
19.如图,是由一些小立方块所搭几何体的三种视图,若在所搭几何体的基础上(不改变原几何体中小立方块的位置),继续添加相同的小立方块,以搭成一个大正方体,至少还需要________个小立方块. /
20.有一个正六面体骰子,放在桌面上,将骰子沿如图所示的顺时针方向滚动,每滚动90°算一次,则滚动第2014次后,骰子朝下一面的点数是________. /
三、解答题(共8题;共60分)
21.一个物体的三视图如图所示,试举例说明物体的形状. /
22.如图,这是一个由大小相等的正方体堆成的几何体的俯视图,小正方形中的数字表示该位置的小正方体的个数,请你画出它的主视图和左视图. /
23.画出从三个方向看如图所示的几何体的形状. /
24.已知如图,AB和DE是直立在地面上的两根立柱,AB=5m,某一时刻AB在阳光下的投影BC=2m. (1)请你画出此时DE在阳光下的投影; (2)在测量AB的投影时,同时测量出DE在阳光下的投影长为4m,请你计算DE的长. /
25.如图,图1为一个长方体,AB=AD=16,AE=6,图2为左图的表面展开图,请根据要求回答问题: (1)面“学”的对面是面什么? (2)图1中,M、N为所在棱的中点,试在图2中画出点M、N的位置; 并求出图2中△ABN的面积. /
26.杭州某零件厂刚接到要铸造5000件铁质工件的订单,下面给出了这种工件的三视图.已知铸造这批工件的原料是生铁,待工件铸成后还要在表面涂一层防锈漆,那么完成这批工件需要原料生铁多少吨?涂完这批工件要消耗千克防锈漆?(铁的密度为7.8g/cm3 , 1千克防锈漆可以涂4m2的铁器面,三视图单位为cm) /
27.如图,是由若干个完全相同的小正方体组成的一个几何体. (1)请画出这个几何体的左视图和俯视图;(用阴影表示) (2)如果在这个几何体上再添加一些相同的小正方体,并保持这个几何体的俯视图和左视图不变,那么最多可以再添加几个小正方体? /
28.已知一个几何体的三视图如图所示,试说出它的形状,并根据已知的数据求出这个几何体的侧面积和全面积. /
答案解析部分
一、单选题
1.【答案】A
2.【答案】B
3.【答案】A
4.【答案】B
5.【答案】A
6.【答案】B
7.【答案】A
8.【答案】D
9.【答案】A
10.【答案】B
二、填空题
11.【答案】投影
12.【答案】“学”
13.【答案】3
14.【答案】5
15.【答案】15π
16.【答案】①②③
17.【答案】4m
18.【答案】
80
7
19.【答案】54
20.【答案】3
三、解答题
21.【答案】解:∵此几何体的俯视图是圆环,主视图和左视图均是等腰梯形 ∴该几何体是实心圆台.
22.【答案】/
23.【答案】/
24.【答案】解:(1)如图,EF为此时DE在阳光下的投影; (2)∵AC∥DF, ∴∠ACB=∠DFE, ∴Rt△ABC∽Rt△DEF, ∴
????
????
=
????
????
, 即
5
????
=
2
4
, 解得DE=10(m), 即DE的长为10m. /
25.【答案】解:(1)正方体的表面展开图,相对的面之间一定相隔一个正方形, “学”与“国”是相对面, “叶”与“际”是相对面, “枫”与“校”是相对面, 答:面“学”的对面是面国。 (2)点M、N如图所示, ∵N是所在棱的中点, ∴点N到AB的距离为
1
2
×16=8, ∴△ABN的面积=
1
2
×16×8=64. /
26.【答案】解:∵工件的体积为(30×10+10×10)×20=8000cm3 , ∴重量为8000×7.8=62.4千克, ∴铸造5000件工件需生铁,5000×62.4×10﹣3=312吨, ∵一件工件的表面积为2×(30×20+20×20+10×30+10×10)=2800cm2=0.28m2 . ∴涂完全部工件防锈漆5000×0.28÷4=350千克.
27.【答案】解:(1)画图如下: / (2)在第二层第二列第二行和第三行各加一个;第三层第二列第三行加一个,第三列第三行加1个, 2+1+1=4(个). 故最多可再添加4个小正方体.
28.【答案】解:此几何体为圆锥; ∵半径为3,高为4, ∴圆锥母线长为5, ∴侧面积=2πrR÷2=15π; 全面积=15π+πr2=15π+9π=24π.
一、单选题(共10题;共30分)
1.由7个大小相同的正方体搭成的几何体如图所示,则以下结论:①主视图既是轴对称图形,又是中心对称图形;??? ②俯视图是中心对称图形;③左视图不是中心对称图形;④俯视图和左视图都不是轴对称图形其中正确结论是(??? ) /
A.?①③?????????????????????????????????????B.?①④?????????????????????????????????????C.?②③?????????????????????????????????????D.?②④
2.下列立体图形中,主视图是三角形的是(??? )。
A./B/C/D/
3.一个几何体的三视图如图所示,该几何体是(??? )/
A.?直三棱柱????????????????????????????????/B.?长方体????????????????????????????????/C.?圆锥????????????????????????????????/D.?立方体
4.如图,是由一个圆柱体和一个长方体组成的几何体.其主视图是( ) /
A.?/????????????????/B.?/????????????????/C.?/????????????????/D.?/
5.如图是一个正方体的表面展开图,如果相对面上所标的两个数互为相反数,那么图中x的值是( ) /
A.?8???????????????????????????????????????????/B.?3???????????????????????????????????????????/C.?2???????????????????????????????????????????/D.?-3
6.如图是正方体的展开图,则正方体相对两个面上的数字之和的最小值是 ( ??). /
A.?4???????????????????????????????????????????/B.?6???????????????????????????????????????????/C.?7???????????????????????????????????????????/D.?8
7.如图,D,E,F分别是等边△ABC的边AB,BC,CA的中点,现沿着虚线折起,使A,B,C三点重合,折起后得到的空间图形是(???) /
A.?棱锥????????????????????????????????????B.?圆锥????????????????????????????????????C.?棱柱????????????????????????????????????D.?正方体
8.某几何体的三视图如图所示,则这个几何体是(?? ) /
A.?圆柱?????????????????????????????????????B.?正方体?????????????????????????????????????C.?球?????????????????????????????????????D.?圆锥
9.下图是由八个相同的小正方体组合而成的几何体,其俯视图是(? ????)
/
A.?/??????????????????/B.?/??????????????????/C.?/??????????????????/D.?/
10.如图是一个切去了一个角的正方体纸盒,切面与棱的交点A,B,C均是棱的中点,现将纸盒剪开展成平面,则展开图不可能是( ) /?
A.?/??????????????????/B.?/??????????????????/C.?/??????????????????/D.?/?
二、填空题(共10题;共30分)
11.物体在光线的照射下,会在地面或墙壁上留下它的影子,这就是________现象.
12.小林同学在立方体盒子的每个面上都写了一个字,分别是我、喜、欢、数、学、课,其平面展开图如图所示,那么该立方体盒子上,“我”相对的面上所写的文字是________. /
13.某四棱锥的三视图如图所示,该四棱锥的体积为________. /
14.如图是由大小相同的小正方体组成的简单几何体的左视图和俯视图,那么组成这个几何体的小正方体的个数最少为________?个. /
15.已知圆锥的底面半径是 3????? ,高为 4????? ,则其侧面积为________ ??
??
2
.
16.如图是一个由若干个正方体搭建而成的几何体的主视图与左视图,那么下列图形中可以作为该几何体的俯视图的序号是:________?(多填或错填得0分,少填酌情给分). /
17.如图,林林在A时测得某树的影长为2 m,B时又测得该树的影长为8 m,若两次日照的光线互相垂直,则该树的高度为________? /
18.如图,电影胶片上每一个图片的规格为3.5cm×3.5cm,放映屏幕的规格为2m×2m,若放映机的光源S距胶片20cm,那么光源S距屏幕________?米时,放映的图象刚好布满整个屏幕. /
19.如图,是由一些小立方块所搭几何体的三种视图,若在所搭几何体的基础上(不改变原几何体中小立方块的位置),继续添加相同的小立方块,以搭成一个大正方体,至少还需要________个小立方块. /
20.有一个正六面体骰子,放在桌面上,将骰子沿如图所示的顺时针方向滚动,每滚动90°算一次,则滚动第2014次后,骰子朝下一面的点数是________. /
三、解答题(共8题;共60分)
21.一个物体的三视图如图所示,试举例说明物体的形状. /
22.如图,这是一个由大小相等的正方体堆成的几何体的俯视图,小正方形中的数字表示该位置的小正方体的个数,请你画出它的主视图和左视图. /
23.画出从三个方向看如图所示的几何体的形状. /
24.已知如图,AB和DE是直立在地面上的两根立柱,AB=5m,某一时刻AB在阳光下的投影BC=2m. (1)请你画出此时DE在阳光下的投影; (2)在测量AB的投影时,同时测量出DE在阳光下的投影长为4m,请你计算DE的长. /
25.如图,图1为一个长方体,AB=AD=16,AE=6,图2为左图的表面展开图,请根据要求回答问题: (1)面“学”的对面是面什么? (2)图1中,M、N为所在棱的中点,试在图2中画出点M、N的位置; 并求出图2中△ABN的面积. /
26.杭州某零件厂刚接到要铸造5000件铁质工件的订单,下面给出了这种工件的三视图.已知铸造这批工件的原料是生铁,待工件铸成后还要在表面涂一层防锈漆,那么完成这批工件需要原料生铁多少吨?涂完这批工件要消耗千克防锈漆?(铁的密度为7.8g/cm3 , 1千克防锈漆可以涂4m2的铁器面,三视图单位为cm) /
27.如图,是由若干个完全相同的小正方体组成的一个几何体. (1)请画出这个几何体的左视图和俯视图;(用阴影表示) (2)如果在这个几何体上再添加一些相同的小正方体,并保持这个几何体的俯视图和左视图不变,那么最多可以再添加几个小正方体? /
28.已知一个几何体的三视图如图所示,试说出它的形状,并根据已知的数据求出这个几何体的侧面积和全面积. /
答案解析部分
一、单选题
1.【答案】A
2.【答案】B
3.【答案】A
4.【答案】B
5.【答案】A
6.【答案】B
7.【答案】A
8.【答案】D
9.【答案】A
10.【答案】B
二、填空题
11.【答案】投影
12.【答案】“学”
13.【答案】3
14.【答案】5
15.【答案】15π
16.【答案】①②③
17.【答案】4m
18.【答案】
80
7
19.【答案】54
20.【答案】3
三、解答题
21.【答案】解:∵此几何体的俯视图是圆环,主视图和左视图均是等腰梯形 ∴该几何体是实心圆台.
22.【答案】/
23.【答案】/
24.【答案】解:(1)如图,EF为此时DE在阳光下的投影; (2)∵AC∥DF, ∴∠ACB=∠DFE, ∴Rt△ABC∽Rt△DEF, ∴
????
????
=
????
????
, 即
5
????
=
2
4
, 解得DE=10(m), 即DE的长为10m. /
25.【答案】解:(1)正方体的表面展开图,相对的面之间一定相隔一个正方形, “学”与“国”是相对面, “叶”与“际”是相对面, “枫”与“校”是相对面, 答:面“学”的对面是面国。 (2)点M、N如图所示, ∵N是所在棱的中点, ∴点N到AB的距离为
1
2
×16=8, ∴△ABN的面积=
1
2
×16×8=64. /
26.【答案】解:∵工件的体积为(30×10+10×10)×20=8000cm3 , ∴重量为8000×7.8=62.4千克, ∴铸造5000件工件需生铁,5000×62.4×10﹣3=312吨, ∵一件工件的表面积为2×(30×20+20×20+10×30+10×10)=2800cm2=0.28m2 . ∴涂完全部工件防锈漆5000×0.28÷4=350千克.
27.【答案】解:(1)画图如下: / (2)在第二层第二列第二行和第三行各加一个;第三层第二列第三行加一个,第三列第三行加1个, 2+1+1=4(个). 故最多可再添加4个小正方体.
28.【答案】解:此几何体为圆锥; ∵半径为3,高为4, ∴圆锥母线长为5, ∴侧面积=2πrR÷2=15π; 全面积=15π+πr2=15π+9π=24π.
