第二章+匀变速直线运动的研究+第2节匀变速直线运动的速度与时间的关系+Word版含答案
文档属性
| 名称 | 第二章+匀变速直线运动的研究+第2节匀变速直线运动的速度与时间的关系+Word版含答案 |  | |
| 格式 | zip | ||
| 文件大小 | 718.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 物理 | ||
| 更新时间 | 2019-01-07 13:37:30 | ||
图片预览



文档简介
第2节 匀变速直线运动的速度与时间的关系
一、匀变速直线运动
物体沿直线运动且速度随时间均匀变化(增加或减少).
二、速度与时间的关系
1.公式:v=v0+at.
2.对公式的理解
做匀变速直线运动的物体,在t时刻的速度v等于物体在开始时刻的速度v0加上在整个过程中速度的变化量at.
三、直线运动中的速度—时间图象
1.匀速直线运动的速度—时间图象是一条平行于时间轴的直线.
2.匀变速直线运动的速度—时间图象是一条倾斜的直线.
一、合作探究找规律
考点一 对速度—时间图象的理解
A、B两个物体在同一直线上做匀变速直线运动,它们的速度图象如图所示,二者运动方向相同吗?加速度方向相同吗?哪个物体的加速度较大?
答:二者运动方向相同;加速度方向相反;B物体的加速度较大.
考点二 速度—时间关系的理解及应用
1.物体做匀变速直线运动的速度与时间的关系是哪种类型的函数?函数关系式是怎样的?该函数关系式中各量和匀变速直线运动的速度与时间的关系式中各物理量有怎样的对应关系?
2.物体做匀变速直线运动时一定沿一个方向运动吗?
3.匀变速直线运动有何特点?对应的v-t图象与匀速直线运动的v-t图象有何区别?
答:1.物体做匀变速直线运动的速度与时间的关系是一次函数,函数关系式是y=b+kx,各量和v=v0+at各量的对应关系是:y?v、b?v0、k?a、x?t.
2.不一定.例如物体先做匀减速直线运动,速度减小为0后,又反向做匀加速直线运动,只要整个过程加速度不变,物体就做匀变速直线运动,但前后运动方向相反.
3.匀变速直线运动中,相同时间内的速度变化是相同的;匀变速直线运动的v-t图象为一条倾斜的直线,匀速直线运动的v-t图象为一条平行于t轴的直线.
二、理解概念做判断
1.匀速直线运动的速度是恒定的,不随时间而改变.(√)
2.匀变速直线运动的瞬时速度随时间而均匀改变.(√)
3.速度随时间不断增加的直线运动,一定是匀加速直线运动.(×)
4.公式v=v0+at只适用于匀加速直线运动.(×)
5.由公式v=v0+at知v的方向一定和v0方向一致.(×)
6.在v-t图象中,图线的斜率只与加速度有关.(√)
要点1|匀变速直线运动的理解
1.特点:加速度不变(大小和方向均不变).
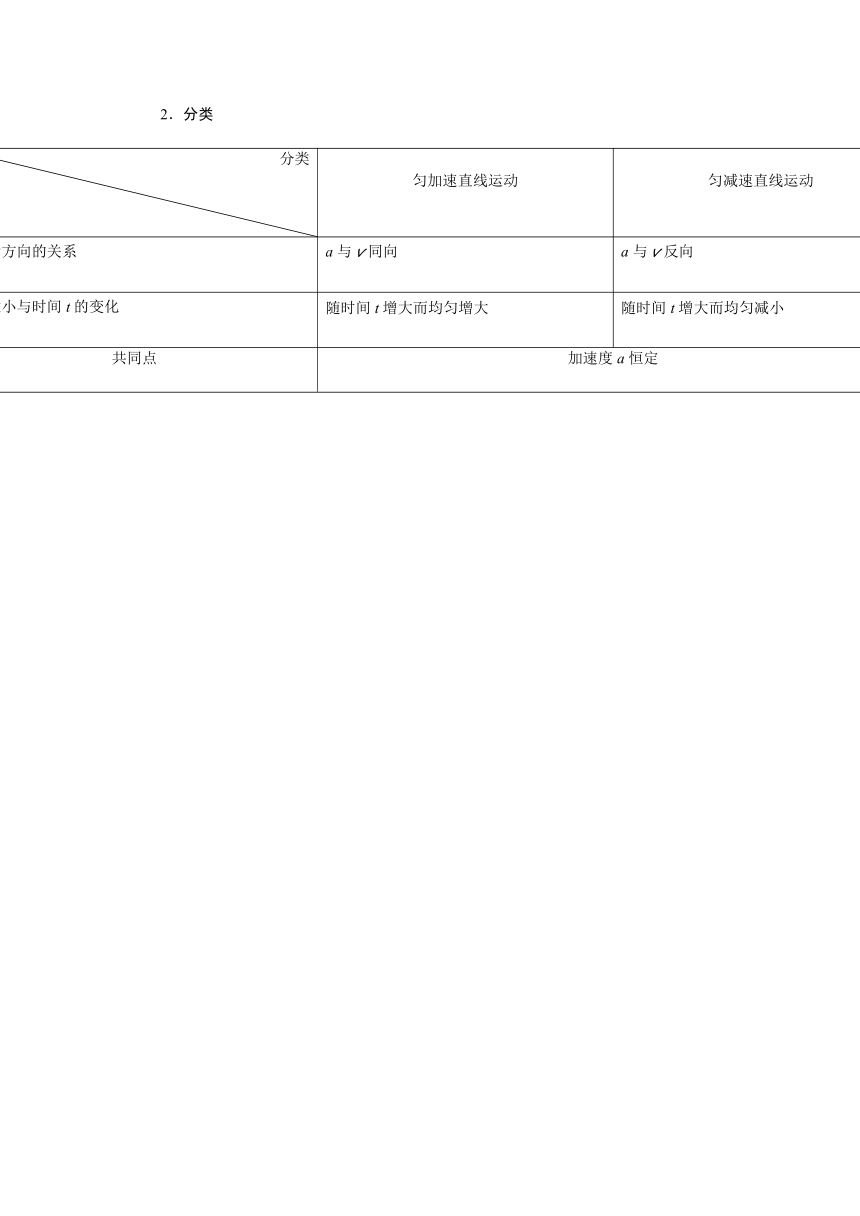
2.分类
分类
特点
匀加速直线运动
匀减速直线运动
a与v方向的关系
a与v同向
a与v反向
v的大小与时间t的变化
随时间t增大而均匀增大
随时间t增大而均匀减小
共同点
加速度a恒定
关于匀变速直线运动,下列说法正确的是( )
A.匀变速直线运动是加速度不变、速度随时间均匀变化的直线运动
B.匀变速直线运动是速度不变、加速度变化的直线运动
C.匀变速直线运动是速度随时间均匀变化、加速度也随时间均匀变化的直线运动
D.当加速度不断减小时,其速度也一定不断减小
【思路点拨】 匀变速直线运动是速度均匀变化的,而加速度a不变.
【解析】 由匀变速直线运动的定义可知,A正确.
【答案】 A
做直线运动的物体在第1 s末、第2 s
末、第3 s末…的速度分别为1 m/s、2 m/s、3 m/s…,则此物体的运动性质是( )
A.匀变速直线运动
B.非匀变速直线运动
C.是加速度不断增大的运动
D.可能是匀变速,也可能是非匀变速直线运动
解析:从已知条件不能确定非整数时刻的速度,即不知道在第1 s末与第2 s末之间速度是否从1 m/s均匀增加到2 m/s,故物体可能做匀变速运动,也可能做非匀变速直线运动.
答案:D
两个关键词透析匀变速直线运动的概念:
(1)轨迹是直线:加速度不变的运动有直线运动,也有曲线运动.物体做直线运动,表明物体的速度方向与加速度方向在同一直线上.
(2)加速度不变:加速度a≠0,且大小和方向均不变;加速度不变表明物体的速度随时间均匀变化,即任意相等的时间内速度的变化均相同.
名师点易错
若物体做匀减速直线运动,当速度减为零时,再反向做匀加速直线运动,加速度的大小和方向与反向前相同,则整个过程物体做的是匀变速直线运动.
要点2|匀变速直线运动的速度公式
1.速度公式
2.公式v=v0+at的理解
(1)对at的理解:由于加速度在数值上等于单位时间内速度的变化量,所以at就是整个运动过程中速度的变化量.
(2)对关系式的理解:t时刻物体的速度等于开始时物体的速度加上运动过程中速度的变化量.
(3)公式的物理意义:描述了做匀变速直线运动的物体其瞬时速度随时间的变化规律.
3.公式v=v0+at的应用
(1)适用范围:物体做匀变速直线运动.
(2)用途:公式v=v0+at中包含四个物理量,不涉及位移,知道了其中任意三个量,就可以求出另外一个物理量.
(3)注意事项:该表达式是矢量式,使用公式时不能简单地将各物理量的数值代入,要首先选择正方向,除时间外将其余各物理量表示成带有正负号的数值后才能代入公式.
4.特殊情况
(1)当v0=0时,v=at,即v∝t.
(2)当a=0时,v=v0(匀速直线运动).
汽车以45 km/h的速度匀速行驶.
(1)若汽车以0.6 m/s2的加速度加速,则10 s后速度能达到多少?
(2)若汽车刹车以0.6 m/s2的加速度减速,则10 s后速度能达到多少?
(3)若汽车刹车以3 m/s2的加速度减速,则10 s后速度为多少?
【思路点拨】 分清加速度的正负,利用v=v0+at来分析.
【解析】 (1)初速度v0=45 km/h=12.5 m/s,加速度a=0.6 m/s2,时间t=10 s.10 s后汽车的速度为v=v0+at=(12.5+0.6×10) m/s=18.5 m/s.
(2)汽车匀减速运动,a1=-0.6 m/s2,减速到停止的时间tm== s≈20.83 s>10 s,
所以10 s后汽车的速度为v=v0+a1t=(12.5-0.6×10) m/s=6.5 m/s.
(3)汽车刹车所用时间t2== s<10 s,
所以10 s后汽车已经刹车完毕,则10 s后汽车速度为零.
【答案】 (1)18.5 m/s (2)6.5 m/s (3)0
磁悬浮列车由静止开始加速出站,加速度为0.6 m/s2,2 min后列车速度为多大?列车匀速运动时速度为432 km/h,如果以0.8 m/s2的加速度减速进站,求减速160 s时速度为多大?
解析:取列车运动方向为正方向.
(1)v=v10+a1t1=(0+0.6×120)m/s=72 m/s=259.2 km/h.
(2)列车减速进站时a2=-0.8 m/s2.
v20=432 km/h=120 m/s.
刹车到速度为0的时间
t0== s=150 s.
所以160 s时列车已经停止运动,速度为0.
答案:259.2 km/h 0
1.v=v0+at的应用技巧:
(1)确定一个方向为正方向(一般以初速度方向为正方向).
(2)依据规定的正方向确定各已知矢量的正、负,并用带有正负的数值表示.
(3)将已知量代入公式进行代数运算,求得v.
(4)根据计算结果说明所求量的大小及方向.
(5)如果要求t或v0,应该先由v=v0+at变形得到t或v0的表达式,再将已知物理量代入进行计算.
2.求解汽车刹车问题时应注意的问题:
汽车刹车、飞机着陆、火车进站等实际减速运动,由于它们在速度减小为零后不再返回,此后它们就一直停留在某位置不动,故计算它们的速度时切不可盲目将所给时间代入速度公式.若所给时间小于刹车用时,则可将所给时间代入速度公式求解,若所给时间大于或等于刹车用时,则它们在所给时间速度为零.
名师点易错
1.速度公式v=v0+at虽然是加速度定义式a=的变形,但两式的适用条件是不同的:v=v0+at仅适用于匀变速直线运动.
2.a=可适用于任意的运动,包括直线运动和曲线运动.
要点3|匀变速直线运动的v-t图象
1.匀速直线运动的v-t图象
如图所示,由于匀速直线运动的速度不随时间改变,因而v-t图象是一条平行于时间轴的直线.从图象中可以直接读出速度的大小和方向.
2.匀变速直线运动的v-t图象
常见v-t图象分析
图象
运动特点
加速度方向为正方向的匀变速直线运动(斜率为正)
加速度方向为负方向的匀变速直线运动(斜率为负)
匀加速直线运动
(远离t轴)
匀减速直线运动
(靠近t轴)
3.对v-t图象的几点说明
(1)纵截距:表示物体的初速度.
(2)横截距:表示物体在开始计时后过一段时间才开始运动,或物体经过一定时间速度变为零.
(3)与横轴的交点:表示速度方向改变的时刻.
(4)图线折点:表示加速度方向改变的时刻.
(5)两图线的交点:表示两物体具有相同的速度.
(6)与坐标轴所围面积:大小等于物体的位移,面积在t轴上方表示位移为正,在t轴下方表示位移为负.
一物体做直线运动的v-t图象如图所示,求2 s末物体的速度大小.
【思路点拨】 找出初速度v0,再找出加速度a,注意分清各量正负,再利用v=v0+at来计算.
【解析】 由题图可知,初速度v0=-1 m/s ,第3 s时的速度 v3=2 m/s,则a== m/s2=1 m/s2,故2 s末物体的速度v2=v0+at2=-1 m/s+1×2 m/s=1 m/s.
【答案】 1 m/s
(多选)如图所示是某物体运动的v-t图象,下列说法正确的是( )
A.该物体的加速度一直不变
B.3 s末物体加速度开始改变
C.0~8 s物体一直做匀减速运动
D.t=0时和t=6 s时物体的速率相等
解析:图线斜率不变,加速度就不变,A正确,B错误;物体先做匀减速运动,再做匀加速运动,C错误;t=0时和t=6 s时,物体的速率都为30 m/s,D正确.
答案:AD
v-t图象的意义:
(1)可求出物体在任一时刻的速度和物体达到某一速度所需要的时间.
(2)图线的斜率等于物体的加速度.
(3)图线与时间轴及始末时刻所围“面积”的数值等于物体在时间t内的位移.在时间轴的上方表示位移为正,在时间轴的下方表示位移为负.
(4)图线在时间轴的上方表示物体向正方向运动,在时间轴的下方表示物体向负方向运动.
(5)可判断物体的运动性质:在v-t图象中,倾斜直线表示物体做匀变速直线运动;平行于时间轴的直线表示物体做匀速直线运动;和时间轴重合的直线表示物体静止.
名师点易错
1.加速度是矢量,既有大小,又有方向,只有加速度大小、方向均不变的直线运动才是匀变速直线运动.
2.只要是加速度不变的直线运动就是匀变速直线运动,无论速度方向是否发生变化.
对点训练一 匀变速直线运动的理解
1.(多选)(2018·包头市东河区期中)关于直线运动下列说法正确的是( )
A.匀速直线运动的速度是恒定的,不随时间而改变
B.匀变速直线运动的瞬时速度随时间而改变
C.速度随时间不断增加的运动,叫匀加速直线运动
D.速度随时间均匀减小的直线运动,通常叫作匀减速直线运动
解析:匀速直线运动的速度是恒定不变的,A选项正确;根据匀变速直线运动的规律可知,其瞬时速度随时间而改变,B选项正确;速度随时间不断增加的运动,加速度不一定恒定,不一定是匀加速直线运动,C选项错误;速度随时间均匀减小的直线运动,通常叫作匀减速直线运动,D选项正确.
答案:ABD
2.物体做匀加速直线运动,已知t=1 s时速度为6 m/s,t=2 s时的速度为8 m/s,下列说法中正确的是( )
A.计时起点t=0时的速度为0
B.物体的加速度为6 m/s2
C.任意1秒内的速度变化为2 m/s
D.第1秒内的平均速度为6 m/s
解析:加速度a== m/s2=2 m/s2,t=0时的速度为(6-2) m/s=4 m/s,故A错误;加速度的值为2 m/s2,故B错误;因加速度为2 m/s2,则任意1 s内的速度变化为2 m/s,故C正确;第1 s内的平均速度为v= m/s=5 m/s,故D错误.
答案:C
对点训练二 匀变速直线运动的图象
3.(多选)某物体运动的速度图象如图所示,根据图象可知( )
A.0~2 s内的加速度为1 m/s2
B.0~5 s内的位移为8 m
C.第1 s末与第3 s末的速度方向相同
D.第1 s末与第4.5 s末加速度方向相同
解析:由速度与时间图象知0~2 s内的加速度为1 m/s2,4~5 s内的加速度为-2 m/s2,故A对,D错;在速度—时间图象中,图线所围面积即为位移,知位移为7 m,B错;时间轴上方的速度都为正值,故C对.
答案:AC
4.如图所示的是甲、乙两物体的v-t图象,由图可知( )
A.甲做匀加速运动,乙做匀减速运动
B.甲、乙两物体相向运动
C.乙比甲晚1 s开始运动
D.5 s末两物体相遇
解析:由图象可知,甲做匀减速直线运动,乙做匀加速运动,故A错误;两个物体的速度均为正值,说明都沿正向运动,甲、乙两物体同向运动,故B错误;甲在t=0时刻开始出发,乙在t=1 s时出发,乙比甲晚1 s出发,故C正确;速度图象与时间轴围成的面积代表物体发生的位移.则知5 s末甲的位移大于乙的位移,它们的出发地点位置关系无法确定,所以t=5 s时,只表示两物体速度相等,不能判断两个物体是否相遇,故D错误.
答案:C
对点训练三 匀变速直线运动的公式
5.以18 m/s的速度行驶的汽车,紧急刹车后做匀减速直线运动,其加速度大小为6 m/s2,求:
(1)汽车在刹车2 s末的速度;
(2)汽车在刹车6 s末的速度.
解析:(1)汽车刹车到停止所需的时间t0== s=3 s>2 s,则2 s末的速度v=v0+at=(18-6×2) m/s=6 m/s,故汽车刹车2 s末的速度为6 m/s.
(2)6 s>3 s,知6 s末的速度为零.
答案:(1)6 m/s (2)0
【强化基础】
1.(2018·温州模拟)如图所示为某医院体检中心的身高测量仪.测量仪顶部向下发射波速为340 m/s的超声波,超声波遇到障碍物后反射回来,被测量仪接收,测量仪记录发射和接收的时间间隔.已知测量仪没有站人时,顶部距离台面3.0 m,当一学生站在台面规定位置后,测量仪记录的时间间隔为0.01 s,则该学生的身高最接近( )
A.110 cm B.130 cm
C.150 cm D.170 cm
解析:根据题干信息可知,学生身高h=h0-×t=130 cm,B选项正确.
答案:B
2.如图所示为A、B两质点的速度图象,其加速度分别为aA、aB,在零时刻的速度分别为vA、vB.那么,下列判断正确的是( )
A.vA<vB B.vA=vB
C.aA>aB D.aA<aB
解析:在v-t图象中,与纵轴的截距表示初速度,则有vA>vB,斜率表示加速度,有aA>aB,故选C.
答案:C
3.(2018·北京市东城区质检)如图所示,某辆汽车在一次刹车过程中,初速度为20 m/s,经过2 s汽车速度减为10 m/s,若将该过程视为匀减速直线运动,则这段时间内汽车加速度的大小为( )
A.2 m/s2 B.5 m/s2
C.15 m/s2 D.20 m/s2
解析:汽车做匀减速直线运动,根据匀变速直线运动的速度—时间公式可知,v=v0-at,解得汽车的加速度a=5 m/s2,B选项正确.
答案:B
4.(多选)甲和乙两个物体在同一条直线上运动,它们的v-t图象分别如图中所示,在t1时刻( )
A.它们的运动方向相同
B.它们的运动方向相反
C.甲的速度比乙的速度大
D.乙的速度比甲的速度大
解析:a、b图线都在t轴上方,速度都为正值,知甲、乙的运动方向相同,故A正确,B错误;由图知,甲的速度比乙的速度小,故C错误,D正确.故选AD.
答案:AD
5.(多选)(2018·十堰期末)一质点做匀变速直线运动,其速度v与时间t的关系为v=4+2t(m/s),关于该质点的运动,下列说法正确的是( )
A.初速度为4 m/s
B.加速度为4 m/s2
C.在第2 s末的速度大小为10 m/s
D.在第2 s末的速度大小为8 m/s
解析:根据匀变速直线运动的速度—时间公式可知,v=v0+at,质点运动的初速度v0=4 m/s,加速度a=2 m/s2,A选项正确,B选项错误;在第2 s末的速度大小为v2=v0+at=8 m/s,C选项错误,D选项正确.
答案:AD
【巩固易错】
6.(2018·北京市大兴区期末)万吨货轮起航,10 s内速度增加到0.2 m/s;火箭发射时,10 s内速度增加到100 m/s;以8 m/s飞行的蜻蜓,能在0.7 s内停下来;以8 m/s行驶的汽车,能在2.5 s内停下来.以上描述的运动中加速度最大的是( )
A.货轮 B.火箭
C.蜻蜓 D.汽车
解析:根据加速度的定义式可知,a=,计算可得货轮的加速度的大小为0.02 m/s2,火箭的加速度大小为10 m/s2,蜻蜓的加速度大小为11.4 m/s2,汽车的加速度大小为3.2 m/s2,蜻蜓的加速度最大,C选项正确.
答案:C
7.(多选)一物体做匀变速直线运动.当t=0时,物体的速度大小为12 m/s,方向向东,当t=2 s时,物体的速度大小为8 m/s,方向仍向东,则当t为多少时,物体的速度大小变为2 m/s( )
A.3 s B.5 s
C.7 s D.9 s
解析:根据加速度的定义式得物体做匀变速直线运动的加速度a==-2 m/s2,根据速度公式v=v0+at,代入数据,当末速度v=2 m/s时,时间t=5 s;当末速度v=-2 m/s时,时间t=7 s,故B、C选项正确.
答案:BC
【能力提升】
8.物体以12 m/s的初速度在水平面上做匀变速直线运动,加速度大小为2 m/s2,求:
(1)若物体做匀加速直线运动,求第4 s末物体的速度;
(2)若物体做匀减速直线运动,求第3 s末物体的速度.
解析:(1)若物体做匀加速运动,则根据速度公式可以得到:v4=v0+at4=12 m/s+2 m/s2×4 s=20 m/s.
(2)若物体做匀减速运动,则根据速度公式可以得到:v3=v0+at3=12 m/s-2 m/s2×3 s=6 m/s.
答案:(1)20 m/s (2)6 m/s
9.卡车原来以10 m/s的速度在平直公路上匀速行驶,因为路口出现红灯,司机从较远的地方即开始刹车,使卡车匀减速前进,当车减速到2 m/s时,交通灯转为绿灯,司机当即放开刹车,并且只用了减速过程的一半时间卡车就加速到了原来的速度,从刹车开始到恢复原速的过程用了12 s.求:
(1)减速与加速过程中的加速度;
(2)开始刹车后2 s末及10 s末的瞬时速度.
解析:(1)卡车先做匀减速直线运动,再做匀加速直线运动,其运动示意图如图所示,设卡车从A点开始减速,则vA=10 m/s,用t1时间到达B点,从B点又开始加速,用时间t2到达C点,则vB=2 m/s,vC=10 m/s,且t2=t1,t1+t2=12 s,可得t1=8 s,t2=4 s.
由v=v0+at得,在AB段,vB=vA+a1t1,①
在BC段,vC=vB+a2t2,②
联立①②两式代入数据解得a1=-1 m/s2,a2=2 m/s2.
(2)2 s末的瞬时速度为v1=vA+a1t′=10 m/s-1×2 m/s=8 m/s,10 s末的瞬时速度为v2=vB+a2t′′=2 m/s+2×(10-8) m/s=6 m/s.
答案:(1)-1 m/s2 2 m/s2
(2)8 m/s 6 m/s
一、匀变速直线运动
物体沿直线运动且速度随时间均匀变化(增加或减少).
二、速度与时间的关系
1.公式:v=v0+at.
2.对公式的理解
做匀变速直线运动的物体,在t时刻的速度v等于物体在开始时刻的速度v0加上在整个过程中速度的变化量at.
三、直线运动中的速度—时间图象
1.匀速直线运动的速度—时间图象是一条平行于时间轴的直线.
2.匀变速直线运动的速度—时间图象是一条倾斜的直线.
一、合作探究找规律
考点一 对速度—时间图象的理解
A、B两个物体在同一直线上做匀变速直线运动,它们的速度图象如图所示,二者运动方向相同吗?加速度方向相同吗?哪个物体的加速度较大?
答:二者运动方向相同;加速度方向相反;B物体的加速度较大.
考点二 速度—时间关系的理解及应用
1.物体做匀变速直线运动的速度与时间的关系是哪种类型的函数?函数关系式是怎样的?该函数关系式中各量和匀变速直线运动的速度与时间的关系式中各物理量有怎样的对应关系?
2.物体做匀变速直线运动时一定沿一个方向运动吗?
3.匀变速直线运动有何特点?对应的v-t图象与匀速直线运动的v-t图象有何区别?
答:1.物体做匀变速直线运动的速度与时间的关系是一次函数,函数关系式是y=b+kx,各量和v=v0+at各量的对应关系是:y?v、b?v0、k?a、x?t.
2.不一定.例如物体先做匀减速直线运动,速度减小为0后,又反向做匀加速直线运动,只要整个过程加速度不变,物体就做匀变速直线运动,但前后运动方向相反.
3.匀变速直线运动中,相同时间内的速度变化是相同的;匀变速直线运动的v-t图象为一条倾斜的直线,匀速直线运动的v-t图象为一条平行于t轴的直线.
二、理解概念做判断
1.匀速直线运动的速度是恒定的,不随时间而改变.(√)
2.匀变速直线运动的瞬时速度随时间而均匀改变.(√)
3.速度随时间不断增加的直线运动,一定是匀加速直线运动.(×)
4.公式v=v0+at只适用于匀加速直线运动.(×)
5.由公式v=v0+at知v的方向一定和v0方向一致.(×)
6.在v-t图象中,图线的斜率只与加速度有关.(√)
要点1|匀变速直线运动的理解
1.特点:加速度不变(大小和方向均不变).
2.分类
分类
特点
匀加速直线运动
匀减速直线运动
a与v方向的关系
a与v同向
a与v反向
v的大小与时间t的变化
随时间t增大而均匀增大
随时间t增大而均匀减小
共同点
加速度a恒定
关于匀变速直线运动,下列说法正确的是( )
A.匀变速直线运动是加速度不变、速度随时间均匀变化的直线运动
B.匀变速直线运动是速度不变、加速度变化的直线运动
C.匀变速直线运动是速度随时间均匀变化、加速度也随时间均匀变化的直线运动
D.当加速度不断减小时,其速度也一定不断减小
【思路点拨】 匀变速直线运动是速度均匀变化的,而加速度a不变.
【解析】 由匀变速直线运动的定义可知,A正确.
【答案】 A
做直线运动的物体在第1 s末、第2 s
末、第3 s末…的速度分别为1 m/s、2 m/s、3 m/s…,则此物体的运动性质是( )
A.匀变速直线运动
B.非匀变速直线运动
C.是加速度不断增大的运动
D.可能是匀变速,也可能是非匀变速直线运动
解析:从已知条件不能确定非整数时刻的速度,即不知道在第1 s末与第2 s末之间速度是否从1 m/s均匀增加到2 m/s,故物体可能做匀变速运动,也可能做非匀变速直线运动.
答案:D
两个关键词透析匀变速直线运动的概念:
(1)轨迹是直线:加速度不变的运动有直线运动,也有曲线运动.物体做直线运动,表明物体的速度方向与加速度方向在同一直线上.
(2)加速度不变:加速度a≠0,且大小和方向均不变;加速度不变表明物体的速度随时间均匀变化,即任意相等的时间内速度的变化均相同.
名师点易错
若物体做匀减速直线运动,当速度减为零时,再反向做匀加速直线运动,加速度的大小和方向与反向前相同,则整个过程物体做的是匀变速直线运动.
要点2|匀变速直线运动的速度公式
1.速度公式
2.公式v=v0+at的理解
(1)对at的理解:由于加速度在数值上等于单位时间内速度的变化量,所以at就是整个运动过程中速度的变化量.
(2)对关系式的理解:t时刻物体的速度等于开始时物体的速度加上运动过程中速度的变化量.
(3)公式的物理意义:描述了做匀变速直线运动的物体其瞬时速度随时间的变化规律.
3.公式v=v0+at的应用
(1)适用范围:物体做匀变速直线运动.
(2)用途:公式v=v0+at中包含四个物理量,不涉及位移,知道了其中任意三个量,就可以求出另外一个物理量.
(3)注意事项:该表达式是矢量式,使用公式时不能简单地将各物理量的数值代入,要首先选择正方向,除时间外将其余各物理量表示成带有正负号的数值后才能代入公式.
4.特殊情况
(1)当v0=0时,v=at,即v∝t.
(2)当a=0时,v=v0(匀速直线运动).
汽车以45 km/h的速度匀速行驶.
(1)若汽车以0.6 m/s2的加速度加速,则10 s后速度能达到多少?
(2)若汽车刹车以0.6 m/s2的加速度减速,则10 s后速度能达到多少?
(3)若汽车刹车以3 m/s2的加速度减速,则10 s后速度为多少?
【思路点拨】 分清加速度的正负,利用v=v0+at来分析.
【解析】 (1)初速度v0=45 km/h=12.5 m/s,加速度a=0.6 m/s2,时间t=10 s.10 s后汽车的速度为v=v0+at=(12.5+0.6×10) m/s=18.5 m/s.
(2)汽车匀减速运动,a1=-0.6 m/s2,减速到停止的时间tm== s≈20.83 s>10 s,
所以10 s后汽车的速度为v=v0+a1t=(12.5-0.6×10) m/s=6.5 m/s.
(3)汽车刹车所用时间t2== s<10 s,
所以10 s后汽车已经刹车完毕,则10 s后汽车速度为零.
【答案】 (1)18.5 m/s (2)6.5 m/s (3)0
磁悬浮列车由静止开始加速出站,加速度为0.6 m/s2,2 min后列车速度为多大?列车匀速运动时速度为432 km/h,如果以0.8 m/s2的加速度减速进站,求减速160 s时速度为多大?
解析:取列车运动方向为正方向.
(1)v=v10+a1t1=(0+0.6×120)m/s=72 m/s=259.2 km/h.
(2)列车减速进站时a2=-0.8 m/s2.
v20=432 km/h=120 m/s.
刹车到速度为0的时间
t0== s=150 s.
所以160 s时列车已经停止运动,速度为0.
答案:259.2 km/h 0
1.v=v0+at的应用技巧:
(1)确定一个方向为正方向(一般以初速度方向为正方向).
(2)依据规定的正方向确定各已知矢量的正、负,并用带有正负的数值表示.
(3)将已知量代入公式进行代数运算,求得v.
(4)根据计算结果说明所求量的大小及方向.
(5)如果要求t或v0,应该先由v=v0+at变形得到t或v0的表达式,再将已知物理量代入进行计算.
2.求解汽车刹车问题时应注意的问题:
汽车刹车、飞机着陆、火车进站等实际减速运动,由于它们在速度减小为零后不再返回,此后它们就一直停留在某位置不动,故计算它们的速度时切不可盲目将所给时间代入速度公式.若所给时间小于刹车用时,则可将所给时间代入速度公式求解,若所给时间大于或等于刹车用时,则它们在所给时间速度为零.
名师点易错
1.速度公式v=v0+at虽然是加速度定义式a=的变形,但两式的适用条件是不同的:v=v0+at仅适用于匀变速直线运动.
2.a=可适用于任意的运动,包括直线运动和曲线运动.
要点3|匀变速直线运动的v-t图象
1.匀速直线运动的v-t图象
如图所示,由于匀速直线运动的速度不随时间改变,因而v-t图象是一条平行于时间轴的直线.从图象中可以直接读出速度的大小和方向.
2.匀变速直线运动的v-t图象
常见v-t图象分析
图象
运动特点
加速度方向为正方向的匀变速直线运动(斜率为正)
加速度方向为负方向的匀变速直线运动(斜率为负)
匀加速直线运动
(远离t轴)
匀减速直线运动
(靠近t轴)
3.对v-t图象的几点说明
(1)纵截距:表示物体的初速度.
(2)横截距:表示物体在开始计时后过一段时间才开始运动,或物体经过一定时间速度变为零.
(3)与横轴的交点:表示速度方向改变的时刻.
(4)图线折点:表示加速度方向改变的时刻.
(5)两图线的交点:表示两物体具有相同的速度.
(6)与坐标轴所围面积:大小等于物体的位移,面积在t轴上方表示位移为正,在t轴下方表示位移为负.
一物体做直线运动的v-t图象如图所示,求2 s末物体的速度大小.
【思路点拨】 找出初速度v0,再找出加速度a,注意分清各量正负,再利用v=v0+at来计算.
【解析】 由题图可知,初速度v0=-1 m/s ,第3 s时的速度 v3=2 m/s,则a== m/s2=1 m/s2,故2 s末物体的速度v2=v0+at2=-1 m/s+1×2 m/s=1 m/s.
【答案】 1 m/s
(多选)如图所示是某物体运动的v-t图象,下列说法正确的是( )
A.该物体的加速度一直不变
B.3 s末物体加速度开始改变
C.0~8 s物体一直做匀减速运动
D.t=0时和t=6 s时物体的速率相等
解析:图线斜率不变,加速度就不变,A正确,B错误;物体先做匀减速运动,再做匀加速运动,C错误;t=0时和t=6 s时,物体的速率都为30 m/s,D正确.
答案:AD
v-t图象的意义:
(1)可求出物体在任一时刻的速度和物体达到某一速度所需要的时间.
(2)图线的斜率等于物体的加速度.
(3)图线与时间轴及始末时刻所围“面积”的数值等于物体在时间t内的位移.在时间轴的上方表示位移为正,在时间轴的下方表示位移为负.
(4)图线在时间轴的上方表示物体向正方向运动,在时间轴的下方表示物体向负方向运动.
(5)可判断物体的运动性质:在v-t图象中,倾斜直线表示物体做匀变速直线运动;平行于时间轴的直线表示物体做匀速直线运动;和时间轴重合的直线表示物体静止.
名师点易错
1.加速度是矢量,既有大小,又有方向,只有加速度大小、方向均不变的直线运动才是匀变速直线运动.
2.只要是加速度不变的直线运动就是匀变速直线运动,无论速度方向是否发生变化.
对点训练一 匀变速直线运动的理解
1.(多选)(2018·包头市东河区期中)关于直线运动下列说法正确的是( )
A.匀速直线运动的速度是恒定的,不随时间而改变
B.匀变速直线运动的瞬时速度随时间而改变
C.速度随时间不断增加的运动,叫匀加速直线运动
D.速度随时间均匀减小的直线运动,通常叫作匀减速直线运动
解析:匀速直线运动的速度是恒定不变的,A选项正确;根据匀变速直线运动的规律可知,其瞬时速度随时间而改变,B选项正确;速度随时间不断增加的运动,加速度不一定恒定,不一定是匀加速直线运动,C选项错误;速度随时间均匀减小的直线运动,通常叫作匀减速直线运动,D选项正确.
答案:ABD
2.物体做匀加速直线运动,已知t=1 s时速度为6 m/s,t=2 s时的速度为8 m/s,下列说法中正确的是( )
A.计时起点t=0时的速度为0
B.物体的加速度为6 m/s2
C.任意1秒内的速度变化为2 m/s
D.第1秒内的平均速度为6 m/s
解析:加速度a== m/s2=2 m/s2,t=0时的速度为(6-2) m/s=4 m/s,故A错误;加速度的值为2 m/s2,故B错误;因加速度为2 m/s2,则任意1 s内的速度变化为2 m/s,故C正确;第1 s内的平均速度为v= m/s=5 m/s,故D错误.
答案:C
对点训练二 匀变速直线运动的图象
3.(多选)某物体运动的速度图象如图所示,根据图象可知( )
A.0~2 s内的加速度为1 m/s2
B.0~5 s内的位移为8 m
C.第1 s末与第3 s末的速度方向相同
D.第1 s末与第4.5 s末加速度方向相同
解析:由速度与时间图象知0~2 s内的加速度为1 m/s2,4~5 s内的加速度为-2 m/s2,故A对,D错;在速度—时间图象中,图线所围面积即为位移,知位移为7 m,B错;时间轴上方的速度都为正值,故C对.
答案:AC
4.如图所示的是甲、乙两物体的v-t图象,由图可知( )
A.甲做匀加速运动,乙做匀减速运动
B.甲、乙两物体相向运动
C.乙比甲晚1 s开始运动
D.5 s末两物体相遇
解析:由图象可知,甲做匀减速直线运动,乙做匀加速运动,故A错误;两个物体的速度均为正值,说明都沿正向运动,甲、乙两物体同向运动,故B错误;甲在t=0时刻开始出发,乙在t=1 s时出发,乙比甲晚1 s出发,故C正确;速度图象与时间轴围成的面积代表物体发生的位移.则知5 s末甲的位移大于乙的位移,它们的出发地点位置关系无法确定,所以t=5 s时,只表示两物体速度相等,不能判断两个物体是否相遇,故D错误.
答案:C
对点训练三 匀变速直线运动的公式
5.以18 m/s的速度行驶的汽车,紧急刹车后做匀减速直线运动,其加速度大小为6 m/s2,求:
(1)汽车在刹车2 s末的速度;
(2)汽车在刹车6 s末的速度.
解析:(1)汽车刹车到停止所需的时间t0== s=3 s>2 s,则2 s末的速度v=v0+at=(18-6×2) m/s=6 m/s,故汽车刹车2 s末的速度为6 m/s.
(2)6 s>3 s,知6 s末的速度为零.
答案:(1)6 m/s (2)0
【强化基础】
1.(2018·温州模拟)如图所示为某医院体检中心的身高测量仪.测量仪顶部向下发射波速为340 m/s的超声波,超声波遇到障碍物后反射回来,被测量仪接收,测量仪记录发射和接收的时间间隔.已知测量仪没有站人时,顶部距离台面3.0 m,当一学生站在台面规定位置后,测量仪记录的时间间隔为0.01 s,则该学生的身高最接近( )
A.110 cm B.130 cm
C.150 cm D.170 cm
解析:根据题干信息可知,学生身高h=h0-×t=130 cm,B选项正确.
答案:B
2.如图所示为A、B两质点的速度图象,其加速度分别为aA、aB,在零时刻的速度分别为vA、vB.那么,下列判断正确的是( )
A.vA<vB B.vA=vB
C.aA>aB D.aA<aB
解析:在v-t图象中,与纵轴的截距表示初速度,则有vA>vB,斜率表示加速度,有aA>aB,故选C.
答案:C
3.(2018·北京市东城区质检)如图所示,某辆汽车在一次刹车过程中,初速度为20 m/s,经过2 s汽车速度减为10 m/s,若将该过程视为匀减速直线运动,则这段时间内汽车加速度的大小为( )
A.2 m/s2 B.5 m/s2
C.15 m/s2 D.20 m/s2
解析:汽车做匀减速直线运动,根据匀变速直线运动的速度—时间公式可知,v=v0-at,解得汽车的加速度a=5 m/s2,B选项正确.
答案:B
4.(多选)甲和乙两个物体在同一条直线上运动,它们的v-t图象分别如图中所示,在t1时刻( )
A.它们的运动方向相同
B.它们的运动方向相反
C.甲的速度比乙的速度大
D.乙的速度比甲的速度大
解析:a、b图线都在t轴上方,速度都为正值,知甲、乙的运动方向相同,故A正确,B错误;由图知,甲的速度比乙的速度小,故C错误,D正确.故选AD.
答案:AD
5.(多选)(2018·十堰期末)一质点做匀变速直线运动,其速度v与时间t的关系为v=4+2t(m/s),关于该质点的运动,下列说法正确的是( )
A.初速度为4 m/s
B.加速度为4 m/s2
C.在第2 s末的速度大小为10 m/s
D.在第2 s末的速度大小为8 m/s
解析:根据匀变速直线运动的速度—时间公式可知,v=v0+at,质点运动的初速度v0=4 m/s,加速度a=2 m/s2,A选项正确,B选项错误;在第2 s末的速度大小为v2=v0+at=8 m/s,C选项错误,D选项正确.
答案:AD
【巩固易错】
6.(2018·北京市大兴区期末)万吨货轮起航,10 s内速度增加到0.2 m/s;火箭发射时,10 s内速度增加到100 m/s;以8 m/s飞行的蜻蜓,能在0.7 s内停下来;以8 m/s行驶的汽车,能在2.5 s内停下来.以上描述的运动中加速度最大的是( )
A.货轮 B.火箭
C.蜻蜓 D.汽车
解析:根据加速度的定义式可知,a=,计算可得货轮的加速度的大小为0.02 m/s2,火箭的加速度大小为10 m/s2,蜻蜓的加速度大小为11.4 m/s2,汽车的加速度大小为3.2 m/s2,蜻蜓的加速度最大,C选项正确.
答案:C
7.(多选)一物体做匀变速直线运动.当t=0时,物体的速度大小为12 m/s,方向向东,当t=2 s时,物体的速度大小为8 m/s,方向仍向东,则当t为多少时,物体的速度大小变为2 m/s( )
A.3 s B.5 s
C.7 s D.9 s
解析:根据加速度的定义式得物体做匀变速直线运动的加速度a==-2 m/s2,根据速度公式v=v0+at,代入数据,当末速度v=2 m/s时,时间t=5 s;当末速度v=-2 m/s时,时间t=7 s,故B、C选项正确.
答案:BC
【能力提升】
8.物体以12 m/s的初速度在水平面上做匀变速直线运动,加速度大小为2 m/s2,求:
(1)若物体做匀加速直线运动,求第4 s末物体的速度;
(2)若物体做匀减速直线运动,求第3 s末物体的速度.
解析:(1)若物体做匀加速运动,则根据速度公式可以得到:v4=v0+at4=12 m/s+2 m/s2×4 s=20 m/s.
(2)若物体做匀减速运动,则根据速度公式可以得到:v3=v0+at3=12 m/s-2 m/s2×3 s=6 m/s.
答案:(1)20 m/s (2)6 m/s
9.卡车原来以10 m/s的速度在平直公路上匀速行驶,因为路口出现红灯,司机从较远的地方即开始刹车,使卡车匀减速前进,当车减速到2 m/s时,交通灯转为绿灯,司机当即放开刹车,并且只用了减速过程的一半时间卡车就加速到了原来的速度,从刹车开始到恢复原速的过程用了12 s.求:
(1)减速与加速过程中的加速度;
(2)开始刹车后2 s末及10 s末的瞬时速度.
解析:(1)卡车先做匀减速直线运动,再做匀加速直线运动,其运动示意图如图所示,设卡车从A点开始减速,则vA=10 m/s,用t1时间到达B点,从B点又开始加速,用时间t2到达C点,则vB=2 m/s,vC=10 m/s,且t2=t1,t1+t2=12 s,可得t1=8 s,t2=4 s.
由v=v0+at得,在AB段,vB=vA+a1t1,①
在BC段,vC=vB+a2t2,②
联立①②两式代入数据解得a1=-1 m/s2,a2=2 m/s2.
(2)2 s末的瞬时速度为v1=vA+a1t′=10 m/s-1×2 m/s=8 m/s,10 s末的瞬时速度为v2=vB+a2t′′=2 m/s+2×(10-8) m/s=6 m/s.
答案:(1)-1 m/s2 2 m/s2
(2)8 m/s 6 m/s
同课章节目录
- 第一章 运动的描述
- 绪论
- 1 质点 参考系和坐标系
- 2 时间和位移
- 3 运动快慢的描述──速度
- 4 实验:用打点计时器测速度
- 5 速度变化快慢的描述──加速度
- 第二章 匀变速直线运动的研究
- 1 实验:探究小车速度随时间变化的规律
- 2 匀变速直线运动的速度与时间的关系
- 3 匀变速直线运动的位移与时间的关系
- 4 匀变速直线运动的位移与速度的关系
- 5 自由落体运动
- 6 伽利略对自由落体运动的研究
- 第三章 相互作用
- 1 重力 基本相互作用
- 2 弹力
- 3 摩擦力
- 4 力的合成
- 5 力的分解
- 第四章 牛顿运动定律
- 1 牛顿第一定律
- 2 实验:探究加速度与力、质量的关系
- 3 牛顿第二定律
- 4 力学单位制
- 5 牛顿第三定律
- 6 用牛顿定律解决问题(一)
- 7 用牛顿定律解决问题(二)
