2017-2018学年度第一学期沪科版九年级数学上册第23章解直角三角形单元检测试题
文档属性
| 名称 | 2017-2018学年度第一学期沪科版九年级数学上册第23章解直角三角形单元检测试题 |  | |
| 格式 | zip | ||
| 文件大小 | 179.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-01-07 20:15:03 | ||
图片预览



文档简介
2017-2018学年度第一学期沪科版九年级数学上册
第23章 解直角三角形 单元检测试题
考试总分: 120 分 考试时间: 120 分钟
学校:__________ 班级:__________ 姓名:__________ 考号:__________
一、选择题(共 10 小题 ,每小题 3 分 ,共 30 分 )
?1.在中,已知,,,则等于( )
A. B. C. D.
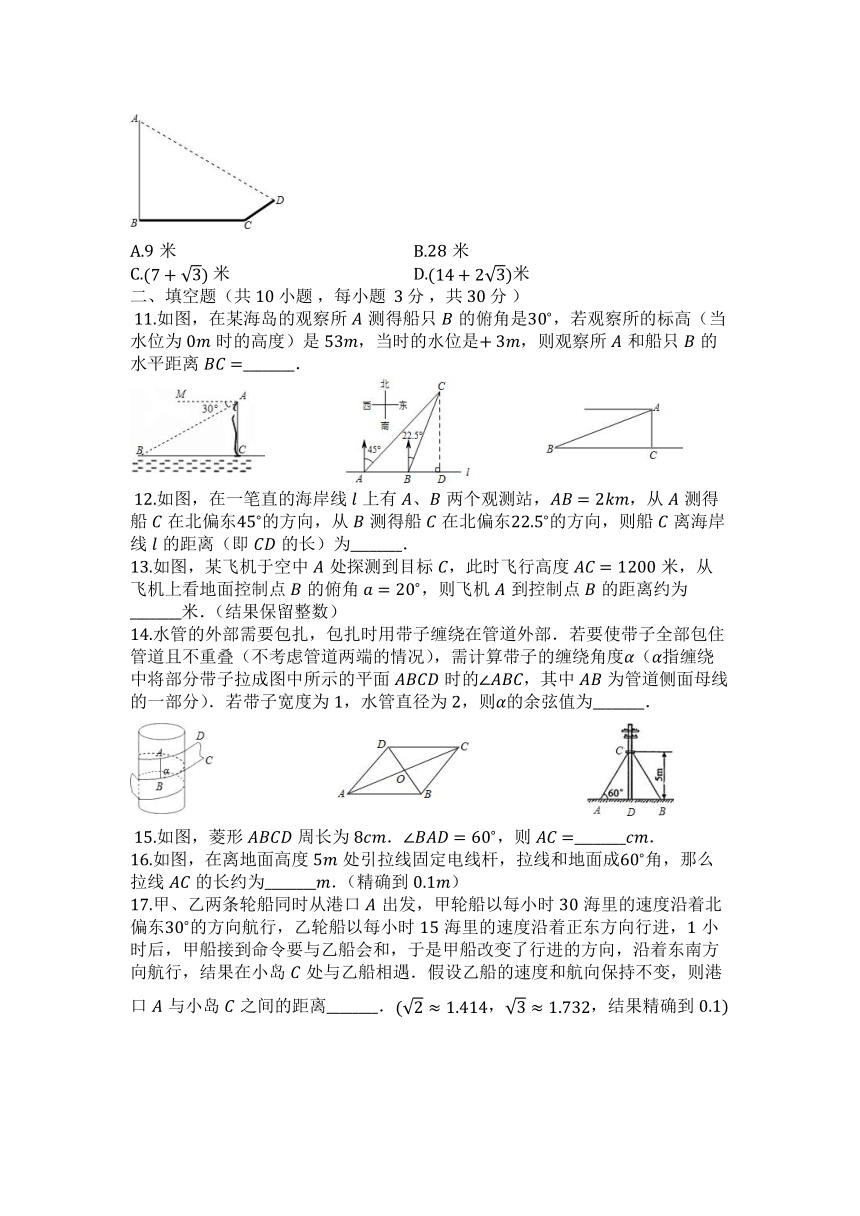
?2.如图,坡角为的斜坡上两树间的水平距离为,则两树间的坡面距离为( )
A. B. C. D.
?3.如图,海地地震后,抢险队派一架直升机去,两个村庄抢险,飞机在距地面米上空的点,测得村的俯角为,测得村的俯角为,则两村相距多少米?( )
A.米 B.米
C.米 D.米
?4.数学活动课上,小敏、小颖分别画了和,数据如图,如果把小敏画的三角形面积记作,小颖画的三角形面积记作,那么你认为( )
A. B.
C. D.不能确定
?5.如图所示,是平面镜,光线从点出发经上的点反射后到达点,若入射角为,,,垂足分别为,,且,,,则的值是( )
A. B. C. D.
?
6.海中有一个小岛,它的周围海里内有暗礁,渔船跟踪鱼群由西向东航行,在点测得小岛在北偏东方向上,航行海里到达点,这是测得小岛在北偏东方向上.若渔船不改变航线继续向东航行而没有触礁危险,则的最大值为( )
A. B. C. D.
?7.一座楼梯的示意图如图所示,是铅垂线,是水平线,与的夹角为.现要在楼梯上铺一条地毯,已知米,楼梯宽度米,则地毯的面积至少需要( )
A.米 B.米
C.米 D.米
?8.如图,马航失联后,“海巡”船匀速在印度洋搜救,当它行驶到处时,发现它的北偏东方向有一灯塔,海巡船继续向北航行小时后到达处,发现灯塔在它的北偏东方向.若海巡船继续向北航行,那么要再过多少时间海巡船离灯塔最近?( )
A.小时 B.小时
C.小时 D.小时
?9.已知小芳站在层高为米的六层楼的屋顶上来估计旁边一支烟囱的高度,当小芳以俯角向下看时,刚好可以看到烟囱的底部,当小芳以仰角向上看时,刚好可以看到烟囱的顶部,若小芳的身高为米,请你估计烟囱的高度(,结果保留三个有效数字)( )
A.米 B.米
C.米 D.米
?10.在土坡的坡面和地面上,量得米,米,与地面成角,且此时测得米杆的影长为米,则电线杆的高度为( )
A.米 B.米
C.?米 D.米
二、填空题(共 10 小题 ,每小题 3 分 ,共 30 分 )
?11.如图,在某海岛的观察所测得船只的俯角是,若观察所的标高(当水位为时的高度)是,当时的水位是,则观察所和船只的水平距离________.
?12.如图,在一笔直的海岸线上有、两个观测站,,从测得船在北偏东的方向,从测得船在北偏东的方向,则船离海岸线的距离(即的长)为________.
13.如图,某飞机于空中处探测到目标,此时飞行高度米,从飞机上看地面控制点的俯角,则飞机到控制点的距离约为________米.(结果保留整数)
14.水管的外部需要包扎,包扎时用带子缠绕在管道外部.若要使带子全部包住管道且不重叠(不考虑管道两端的情况),需计算带子的缠绕角度(指缠绕中将部分带子拉成图中所示的平面时的,其中为管道侧面母线的一部分).若带子宽度为,水管直径为,则的余弦值为________.
?15.如图,菱形周长为.,则________.
16.如图,在离地面高度处引拉线固定电线杆,拉线和地面成角,那么拉线的长约为________.(精确到)
17.甲、乙两条轮船同时从港口出发,甲轮船以每小时海里的速度沿着北偏东的方向航行,乙轮船以每小时海里的速度沿着正东方向行进,小时后,甲船接到命令要与乙船会和,于是甲船改变了行进的方向,沿着东南方向航行,结果在小岛处与乙船相遇.假设乙船的速度和航向保持不变,则港口与小岛之间的距离________.,,结果精确到
?18.学校校园内有块如图所示的三角形空地,计划将这块空地建成一个花园,以美化环境,预计花园每平方米造价为元,学校建这个花园至少需要投资________元.
?19.有一拦水坝的横断面是等腰梯形,它的上底长为,下底长为,高为,则此拦水坝斜坡的坡度为________.
?20.如图,是平面镜,光线从点出发经上点反射照到点,若入射角为,,,且,,,则值为________.
三、解答题(共 6 小题 ,每小题 10 分 ,共 60 分 )
?21.如图,、两地之间有一座山,汽车原来从地到地经过地沿折线行驶,现开通隧道后,汽车直接沿直线行驶.已知千米,,.则隧道开通后,汽车从地到地比原来少走多少千米?(结果保留根号)
?
22.如图,小山岗的斜坡的坡度是,在与山脚距离米的处,测得山顶的仰角为,求小山岗的高(结果取整数)
参考数据:,,.
?
23.如图,大海中有和两个岛屿,为测量它们之间的距离,在海岸线上点处测得,;在点处测得,,.
判断线段与的数量关系,并说明理由;
求两个岛屿和之间的距离.
?
24.如图,在某海域内有三个港口、、.港口在港口北偏东方向上,港口在港口北偏西方向上.一艘船以每小时海里的速度沿北偏东的方向驶离港口小时后到达点位置处,此时发现船舱漏水,海水以每分钟吨的速度渗入船内.当船舱渗入的海水总量超过吨时,船将沉入海中.同时在处测得港口在处的南偏东方向上.若船上的抽水机每小时可将吨的海水排出船外,问此船在处至少应以怎样的航行速度驶向最近的港口停靠,才能保证船在抵达港口前不会沉没(要求计算结果保留根号)?并指出此时船的航行方向.
?
25.某校初三年级“数学兴趣小组”实地测量操场旗杆的高度.旗杆的影子落在操场和操场边的土坡上,如图所示,测得在操场上的影长,斜坡上的影长,已知斜坡与操场平面的夹角为,同时测得身高的学生在操场?上的影长为.求旗杆的高度.(结果精确到)
(提示:同一时刻物高与影长成正比.参考数据:)
?
26.如图,重庆某广场新建与建筑物垂直的空中玻璃走廊与相连,与地面垂直.在处测得建筑物顶端的仰角为,测得建筑物处的仰角为(不计测量人员的身高),为米.图中的点、、、、及直线均在同一平面内.
求、两点的高度差(结果精确到米);
为方便游客,广场从地面上的点新建扶梯,所在斜面的坡度,到地面的距离为米.一广告牌位于的中点处,市政规划要求在点右侧需留出米的行车道,请判断是否需要挪走广告牌,并说明理由.(参考数据:,,,,)
答案
1.C
2.C
3.B
4.C
5.D
6.B
7.D
8.B
9.B
10.D
11.
12.
13.
14.
15.
16.
17.海里
18.
19.
20.
21.汽车从地到地比原来少走千米.
22.解:在直角三角形中,
∵,
∴.?????
在直角三角形中,
∵,
∴.
∴.???
∵,
∴.??????
解得:米.?????????????????
∴小山岗的高度为米.
23.两个岛屿与之间的距离约为.
24.此船应转向沿南偏东的方向向港口航行,且航行速度至少不低于每小时海里,才能保证船在抵达港口前不会沉没.
25.解:过作垂直的延长线于,且过作于,
∵在中,米,
∴米,米,
∴米,米,
∵身高的学生在操场?上的影长为.
∴,
则米,
米.
∴电线杆的高度为米.
26.解:在中,,
在中,,
∴米;∵米,
∴米,
在中,,
∴米米,
∴需要挪走广告牌.
第23章 解直角三角形 单元检测试题
考试总分: 120 分 考试时间: 120 分钟
学校:__________ 班级:__________ 姓名:__________ 考号:__________
一、选择题(共 10 小题 ,每小题 3 分 ,共 30 分 )
?1.在中,已知,,,则等于( )
A. B. C. D.
?2.如图,坡角为的斜坡上两树间的水平距离为,则两树间的坡面距离为( )
A. B. C. D.
?3.如图,海地地震后,抢险队派一架直升机去,两个村庄抢险,飞机在距地面米上空的点,测得村的俯角为,测得村的俯角为,则两村相距多少米?( )
A.米 B.米
C.米 D.米
?4.数学活动课上,小敏、小颖分别画了和,数据如图,如果把小敏画的三角形面积记作,小颖画的三角形面积记作,那么你认为( )
A. B.
C. D.不能确定
?5.如图所示,是平面镜,光线从点出发经上的点反射后到达点,若入射角为,,,垂足分别为,,且,,,则的值是( )
A. B. C. D.
?
6.海中有一个小岛,它的周围海里内有暗礁,渔船跟踪鱼群由西向东航行,在点测得小岛在北偏东方向上,航行海里到达点,这是测得小岛在北偏东方向上.若渔船不改变航线继续向东航行而没有触礁危险,则的最大值为( )
A. B. C. D.
?7.一座楼梯的示意图如图所示,是铅垂线,是水平线,与的夹角为.现要在楼梯上铺一条地毯,已知米,楼梯宽度米,则地毯的面积至少需要( )
A.米 B.米
C.米 D.米
?8.如图,马航失联后,“海巡”船匀速在印度洋搜救,当它行驶到处时,发现它的北偏东方向有一灯塔,海巡船继续向北航行小时后到达处,发现灯塔在它的北偏东方向.若海巡船继续向北航行,那么要再过多少时间海巡船离灯塔最近?( )
A.小时 B.小时
C.小时 D.小时
?9.已知小芳站在层高为米的六层楼的屋顶上来估计旁边一支烟囱的高度,当小芳以俯角向下看时,刚好可以看到烟囱的底部,当小芳以仰角向上看时,刚好可以看到烟囱的顶部,若小芳的身高为米,请你估计烟囱的高度(,结果保留三个有效数字)( )
A.米 B.米
C.米 D.米
?10.在土坡的坡面和地面上,量得米,米,与地面成角,且此时测得米杆的影长为米,则电线杆的高度为( )
A.米 B.米
C.?米 D.米
二、填空题(共 10 小题 ,每小题 3 分 ,共 30 分 )
?11.如图,在某海岛的观察所测得船只的俯角是,若观察所的标高(当水位为时的高度)是,当时的水位是,则观察所和船只的水平距离________.
?12.如图,在一笔直的海岸线上有、两个观测站,,从测得船在北偏东的方向,从测得船在北偏东的方向,则船离海岸线的距离(即的长)为________.
13.如图,某飞机于空中处探测到目标,此时飞行高度米,从飞机上看地面控制点的俯角,则飞机到控制点的距离约为________米.(结果保留整数)
14.水管的外部需要包扎,包扎时用带子缠绕在管道外部.若要使带子全部包住管道且不重叠(不考虑管道两端的情况),需计算带子的缠绕角度(指缠绕中将部分带子拉成图中所示的平面时的,其中为管道侧面母线的一部分).若带子宽度为,水管直径为,则的余弦值为________.
?15.如图,菱形周长为.,则________.
16.如图,在离地面高度处引拉线固定电线杆,拉线和地面成角,那么拉线的长约为________.(精确到)
17.甲、乙两条轮船同时从港口出发,甲轮船以每小时海里的速度沿着北偏东的方向航行,乙轮船以每小时海里的速度沿着正东方向行进,小时后,甲船接到命令要与乙船会和,于是甲船改变了行进的方向,沿着东南方向航行,结果在小岛处与乙船相遇.假设乙船的速度和航向保持不变,则港口与小岛之间的距离________.,,结果精确到
?18.学校校园内有块如图所示的三角形空地,计划将这块空地建成一个花园,以美化环境,预计花园每平方米造价为元,学校建这个花园至少需要投资________元.
?19.有一拦水坝的横断面是等腰梯形,它的上底长为,下底长为,高为,则此拦水坝斜坡的坡度为________.
?20.如图,是平面镜,光线从点出发经上点反射照到点,若入射角为,,,且,,,则值为________.
三、解答题(共 6 小题 ,每小题 10 分 ,共 60 分 )
?21.如图,、两地之间有一座山,汽车原来从地到地经过地沿折线行驶,现开通隧道后,汽车直接沿直线行驶.已知千米,,.则隧道开通后,汽车从地到地比原来少走多少千米?(结果保留根号)
?
22.如图,小山岗的斜坡的坡度是,在与山脚距离米的处,测得山顶的仰角为,求小山岗的高(结果取整数)
参考数据:,,.
?
23.如图,大海中有和两个岛屿,为测量它们之间的距离,在海岸线上点处测得,;在点处测得,,.
判断线段与的数量关系,并说明理由;
求两个岛屿和之间的距离.
?
24.如图,在某海域内有三个港口、、.港口在港口北偏东方向上,港口在港口北偏西方向上.一艘船以每小时海里的速度沿北偏东的方向驶离港口小时后到达点位置处,此时发现船舱漏水,海水以每分钟吨的速度渗入船内.当船舱渗入的海水总量超过吨时,船将沉入海中.同时在处测得港口在处的南偏东方向上.若船上的抽水机每小时可将吨的海水排出船外,问此船在处至少应以怎样的航行速度驶向最近的港口停靠,才能保证船在抵达港口前不会沉没(要求计算结果保留根号)?并指出此时船的航行方向.
?
25.某校初三年级“数学兴趣小组”实地测量操场旗杆的高度.旗杆的影子落在操场和操场边的土坡上,如图所示,测得在操场上的影长,斜坡上的影长,已知斜坡与操场平面的夹角为,同时测得身高的学生在操场?上的影长为.求旗杆的高度.(结果精确到)
(提示:同一时刻物高与影长成正比.参考数据:)
?
26.如图,重庆某广场新建与建筑物垂直的空中玻璃走廊与相连,与地面垂直.在处测得建筑物顶端的仰角为,测得建筑物处的仰角为(不计测量人员的身高),为米.图中的点、、、、及直线均在同一平面内.
求、两点的高度差(结果精确到米);
为方便游客,广场从地面上的点新建扶梯,所在斜面的坡度,到地面的距离为米.一广告牌位于的中点处,市政规划要求在点右侧需留出米的行车道,请判断是否需要挪走广告牌,并说明理由.(参考数据:,,,,)
答案
1.C
2.C
3.B
4.C
5.D
6.B
7.D
8.B
9.B
10.D
11.
12.
13.
14.
15.
16.
17.海里
18.
19.
20.
21.汽车从地到地比原来少走千米.
22.解:在直角三角形中,
∵,
∴.?????
在直角三角形中,
∵,
∴.
∴.???
∵,
∴.??????
解得:米.?????????????????
∴小山岗的高度为米.
23.两个岛屿与之间的距离约为.
24.此船应转向沿南偏东的方向向港口航行,且航行速度至少不低于每小时海里,才能保证船在抵达港口前不会沉没.
25.解:过作垂直的延长线于,且过作于,
∵在中,米,
∴米,米,
∴米,米,
∵身高的学生在操场?上的影长为.
∴,
则米,
米.
∴电线杆的高度为米.
26.解:在中,,
在中,,
∴米;∵米,
∴米,
在中,,
∴米米,
∴需要挪走广告牌.
