10.1 科学探究:杠杆的平衡条件(基础练习)
文档属性
| 名称 | 10.1 科学探究:杠杆的平衡条件(基础练习) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2019-01-08 00:00:00 | ||
图片预览



文档简介
沪科版物理八年级第十章机械与人第一节 科学探究:杠杆的平衡条件
基础练习
一.选择题(共13小题)
1.“给我一个支点和一根足够长的棍,我就能撬起整个地球。”如图所示,生产和生活中的杠杆与阿基米德设想的杠杆属于同一类型的是( )
2.四种剪刀中,最适用于剪开铁皮的是( )
3.如图表示出了人的前臂曲肘时的情况,并标出了支点的位置。当手握重物时,肌肉受到的拉力约是物重的8倍。由此可看出人的这一肌肉杠杆属于( )
A.费力杠杆 B.省力杠杆
C.不省力也不省距离的杠杆 D.既省力又可省距离杠杆
4.如图所示,质量忽略不计的AC硬棒能绕O点转动,在B点挂一物体。在C点施加力F1时,棒刚好处于静止状态。下列说法中正确的是( )
A.此时,F1 的方向向上
B.在C点无论向哪个方向拉,F1大小不变
C.这是一个费力杠杆
D.F1=F2
5.下列工具在正常使用的过程中,可以省距离的是( )
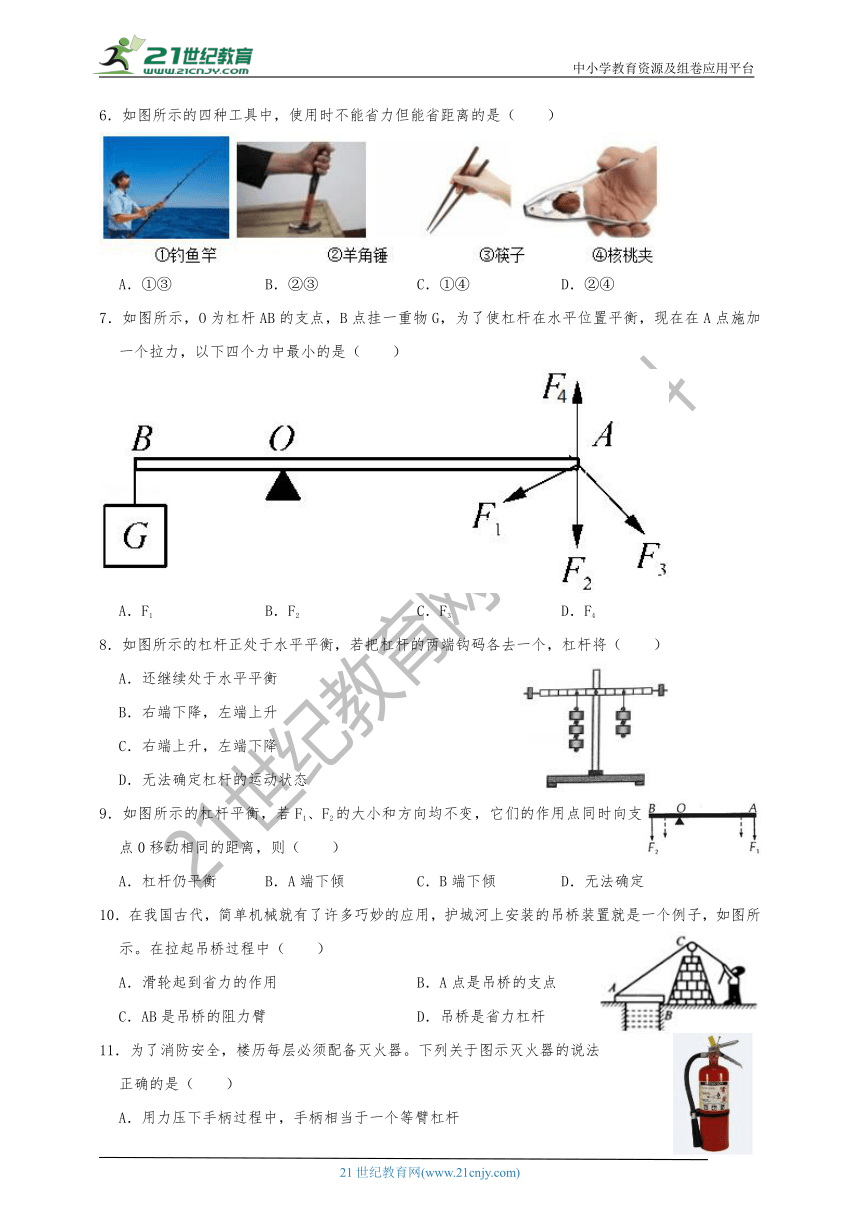
6.如图所示的四种工具中,使用时不能省力但能省距离的是( )
A.①③ B.②③ C.①④ D.②④
7.如图所示,O为杠杆AB的支点,B点挂一重物G,为了使杠杆在水平位置平衡,现在在A点施加一个拉力,以下四个力中最小的是( )
A.F1 B.F2 C.F3 D.F4
8.如图所示的杠杆正处于水平平衡,若把杠杆的两端钩码各去一个,杠杆将( )
A.还继续处于水平平衡
B.右端下降,左端上升
C.右端上升,左端下降
D.无法确定杠杆的运动状态
9.如图所示的杠杆平衡,若F1、F2的大小和方向均不变,它们的作用点同时向支点0移动相同的距离,则( )
A.杠杆仍平衡 B.A端下倾 C.B端下倾 D.无法确定
10.在我国古代,简单机械就有了许多巧妙的应用,护城河上安装的吊桥装置就是一个例子,如图所示。在拉起吊桥过程中( )
A.滑轮起到省力的作用 B.A点是吊桥的支点
C.AB是吊桥的阻力臂 D.吊桥是省力杠杆
11.为了消防安全,楼历每层必须配备灭火器。下列关于图示灭火器的说法正确的是( )
A.用力压下手柄过程中,手柄相当于一个等臂杠杆
B.用力压下手柄过程中,手柄相当于一个费力杠杆
C.干粉能喷出是因为灭火器内的气压等于外界大气压
D.干粉能喷出是因为灭火器内的气压大于外界大气压
12.筷子是东亚文化圈普遍使用的餐具,如图所示将AB这支筷子作为杠杆分,O点为支点,食指指头对筷子上M点的压力FM(垂直于筷子)是动力。则( )
A.阻力臂是MN、动力臂是OM
B.阻力是筷子对食物的压力
C.阻力的方向向上
D.把食物靠近支点放置时,食指对筷子上M点的压力FM变大
13.如图所示的杠杆OC中,拉力F的力臂为( )
A.OB B.OA
C.OC D.BC
二.多选题(共3小题)
14.使用苍蝇拍时,以迅雷不及掩耳之势,轻易拍到苍蝇,这是利用了杠杆的哪个特点( )
A.省力 B.费力 C.省距离 D.费距离
15.在图中,所使用的杠杆属于费力杠杆的是( )
A.① B.② C.③ D.④
16.在我国古代书籍《墨经》中,对杠杆有精辟论述,并有许多巧妙的应用。如图所示是在井上汲水的桔槔,下列对其在使用中不正确的解释是( )
A.桔槔是等臂杠杆,不省力也不费力
B.向井内放送水桶时,人用的力气一定小于水桶的重力,所以省力
C.桔槔是不等臂杠杆,动力臂小于阻力臂,是费力杠杆
D.往上提水时,人用的力气一定小于桶与水的总重,所以省力
三.填空题(共10小题)
17.如图1所示为一种常用核桃夹,用大小相同的力垂直作用在B点比A点更容易夹碎核桃,这说明力的作用效果与 有关。核桃夹是 杠杆。
18.如图2,古希腊学者 最早总结出杠杆平衡条件也称 原理,并说出这样一句豪言壮语:只要给我一个支点,我就可以移动地球。
19.如图3,在用杠杠撬石头的过程中,支点在图中的 点,该杠杆属于 杠杆,在用力方向不变的情况下该人想用更小的力撬起石头,那么他的手应该向 支点的方向移动(选填“远离”或“靠近”)。
20.如图4所示,OB是以O点为支点的杠杆,F是作用在杠杆B端的力。图中线段AB与力F的作用线在一条直线上,且OA⊥AB.线段 (OA/AB/OB)表示力F的力臂,如果拉力一直保持水平方向拉至杠杆到竖直方向,拉力F大小将 (变小/不变/变大)。
21.生活中杠杆的应用十分广泛,比如:①切纸刀②钢丝钳③镊子④摩天轮⑤食品钳。其中属于省力杠杆的有 ,属于费力杠杆有 ,属于等臂杠杆有 。
22.一根水平放置、粗细均匀的木材长0.8m,质量为1.2kg:若将它缓慢竖立起来(如图5所示),至少需要 N的力,需要做的功为 J.(g=10N/kg)
23.在下列工具中:①剪铁皮的剪刀 ②托盘天平 ③筷子 ④定滑轮 ⑤镊子 ⑥羊角锤 ⑦老虎钳 ⑧钓鱼竿,属于省力杠杆的有 ,属于费力杠杆的有 ,属于等臂杠杆的有 。(填序号,漏选错选均不得分)
24.如图6所示,人在划船时,船桨属于 杠杆。船桨在水中移动的距离 手移动的距离,从而加快船前进的速度。
25.如图7所示的甲、乙两棵树,它们的树冠和根系基本相同,只是乙比甲高。当我们研究哪棵树容易被大风吹倒或折断时,可以把树看作是一个 模型,由此可以判断出 树容易被吹倒或折断。
26.将充足气的篮球和套扎在气针尾端的气球一起挂于杠杆左端,调整杠杆右端钩码的悬挂位置,使杠杆平衡(如图8),然后再将扎在气球上的气针头插入篮球的气门内,气球随即膨胀。此时的杠杆的 端将向上翘起,这是因为 的缘故。
四.作图题(共7小题)
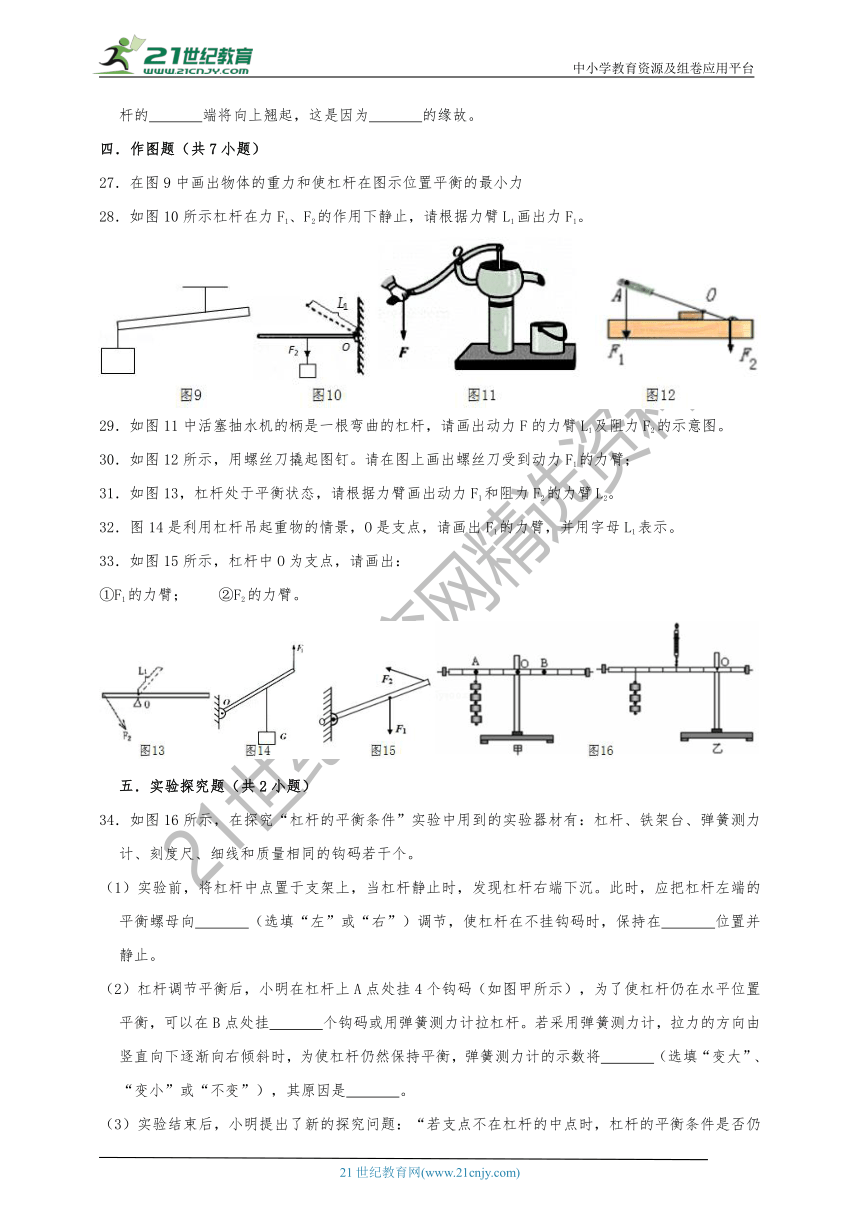
27.在图9中画出物体的重力和使杠杆在图示位置平衡的最小力
28.如图10所示杠杆在力F1、F2的作用下静止,请根据力臂L1画出力F1。
29.如图11中活塞抽水机的柄是一根弯曲的杠杆,请画出动力F的力臂L1及阻力F2的示意图。
30.如图12所示,用螺丝刀撬起图钉。请在图上画出螺丝刀受到动力F1的力臂;
31.如图13,杠杆处于平衡状态,请根据力臂画出动力F1和阻力F2的力臂L2。
32.图14是利用杠杆吊起重物的情景,O是支点,请画出F1的力臂,并用字母L1表示。
33.如图15所示,杠杆中O为支点,请画出:
①F1的力臂; ②F2的力臂。
五.实验探究题(共2小题)
34.如图16所示,在探究“杠杆的平衡条件”实验中用到的实验器材有:杠杆、铁架台、弹簧测力计、刻度尺、细线和质量相同的钩码若干个。
(1)实验前,将杠杆中点置于支架上,当杠杆静止时,发现杠杆右端下沉。此时,应把杠杆左端的平衡螺母向 (选填“左”或“右”)调节,使杠杆在不挂钩码时,保持在 位置并静止。
(2)杠杆调节平衡后,小明在杠杆上A点处挂4个钩码(如图甲所示),为了使杠杆仍在水平位置平衡,可以在B点处挂 个钩码或用弹簧测力计拉杠杆。若采用弹簧测力计,拉力的方向由竖直向下逐渐向右倾斜时,为使杠杆仍然保持平衡,弹簧测力计的示数将 (选填“变大”、“变小”或“不变”),其原因是 。
(3)实验结束后,小明提出了新的探究问题:“若支点不在杠杆的中点时,杠杆的平衡条件是否仍然成立?”于是小明同学利用如图乙所示装置进行探究,发现在杠杆左端的不同位置,用弹簧测力计竖直向上拉使杠杆处于水平平衡时,测出的拉力大小都与杠杆平衡条件不相符,其原因可能是 对实验产生了影响。
(4)关于“杠杆不处于水平位置能否平衡?”小海和小红意见不同。小海认为能平衡,于是他每次让杠杆倾斜到同一位置静止,这样实验也得出了同样的杠杆平衡条件。小海认为杠杆平衡不一定是水平的,这种说法对吗? (填“对”或“错”),小海这种方案与小红让杠杆在水平位置做实验的方案相比较,你认为小海和小红哪位同学的实验方案好?请说明理由:答: 的实验方案好;理由是 。
35.小王利用杠杆进行探究“杠杆的平衡条件”的实验。(每个钩码重0N)
(1)实验前,将杠杆的中点置于支架上,当杠杆静止时,发现杠杆左端下沉,这时应将平衡螺母向 (选填“左”或“右”)端调节,直到杠杆在水平位置平衡;
(2)如图甲所示,①在杠杆A点处挂2个钩码,则在B点处应挂 个同样的钩码,杠杆仍然在水平位置平衡,实验中使杠杆平衡在水平位置的目的是 。
②把B点处的钩码取下,弹簧测力计在B点处施加一个竖直向下的拉力F,杠杆仍在水平位置平衡。当拉力F向右倾斜时,仍要保持杠杆水平平衡,拉力F的大小将 (选填“变大”、“变小”或“不变”),原因是 。
(3)小王对器材进行了改装,又做了如图乙所示的探究,用弹簧测力计在C点竖直向上拉,使杠杆仍然处于水平位置平衡,实验中发现弹簧测力计的示数为3.5N,数据不符合杠杆平衡条件,原因是 。
六.计算题(共3小题)
36.如图所示是搬运泥土的独轮车,设车子和泥土的总重G=1000N,运泥土时从A点竖直提起独轮车把手的力是F1.则:
(1)F1的力臂l1的大小是多少?
(2)F1的大小是多少?
37.如图所示,有一轻质杠杆OA,OB长30厘米,AB长0.9米,A端绳子承受到向上的最大拉力为196牛,要使杠杆水平平衡,B点能挂的物体质量最大为?
38.如图所示的杠杆在细绳的拉力作用下在水平处于平衡状态,已知小球的质量是5kg,放在距离支点10cm处,A点到支点的距离是10cm,求细绳的拉力。(g=10N/kg)
七.解答题(共2小题)
39.有一根杠杆,长度为1m,挂在其一端的物体重为50N,挂在另一端的物体为200N,问:
(1)支点应距左端多远才能使杠杆平衡?
(2)若杠杆两端所挂重物各增加50N,支点应距左端多远才能使杠杆平衡?
40.在学校开展“感恩教育活动”之际,九年级(1)班的大李和小李为敬老院送去一袋重320N的大米,如图所示,扁担长1.6m,O点距大李0.6m,问两人肩上各担多大的力?(不计扁担重)
沪科版物理八年级第十章机械与人第一节 科学探究:杠杆的平衡条件
基础练习参考答案与试题解析
一.选择题(共13小题)
【点评】此题考查的是杠杆的分类,主要包括以下几种:①省力杠杆,动力臂大于阻力臂;②费力杠杆,动力臂小于阻力臂;③等臂杠杆,动力臂等于阻力臂。
2.【分析】结合生活经验和图片,先判断剪刀在使用过程中的目的,再根据各类杠杆的特点选择所需要的剪刀。
【解答】解:
剪开较硬的物体,就需要一把省力的剪刀,因此需选用动力臂大于阻力臂的剪刀,即手柄比刀口长的剪刀,所以D最适合。
故选:D。
【点评】剪刀是生活中一种特殊杠杆,要根据需要选择最合适的。手柄长的剪刀省力,刀口长的剪刀省距离。
3.【分析】要判断杠杆的类型,可依据杠杆的动力臂和阻力臂的大小关系:若动力臂大于阻力臂,是省力杠杆;若动力臂小于阻力臂,是费力杠杆;若动力臂等于阻力臂,则为等臂杠杆。
【解答】解:人的前臂可视为杠杆,当曲肘将茶杯向上举起,支点在下端,此时动力臂小于阻力臂,并且肌肉受到的拉力约是物重的8倍,人的这一肌肉杠杆属于费力杠杆,费力杠杆省距离,故A正确、BCD错。
故选:A。
【点评】本题考查了学生对物理模型的抽象、分析能力。判断杠杆的类型可根据生活经验结合动力臂与阻力臂的大小关系来判断。
4.【分析】(1)由图知,杠杆支点在O,阻力作用在B点,方向向下,为使杠杆静止(处于平衡状态),在C点施加力时,力 的方向需要向上;
(2)由(1)知动力 的方向向上,当垂直于杠杆向上时,动力臂最长,而阻力和阻力臂一定,由杠杆平衡条件可知,此时动力最小;
(3)由于动力臂的大小不能确定,无法得出动力臂和阻力臂的大小关系,无法确定是费力杠杆还是省力杠杆。
【解答】解:
A、如图,杠杆支点在O,阻力作用在B点,方向向下,为使杠杆静止(处于平衡状态),在C点施加力F1时,F1 的方向需要向上,故A正确;
B、F1 的方向向上,当垂直于杠杆向上时,动力臂最长,而阻力和阻力臂一定,由杠杆平衡条件可知,此时动力最小;当动力方向不是垂直于杠杆时,动力变大,故B错;
CD、由于动力臂的大小不能确定,无法得出动力臂和阻力臂的大小关系,无法确定是费力杠杆还是省力杠杆,动力不一定等于阻力,故CD错。
故选:A。
【点评】本题考查了杠杆平衡条件的应用,注意:在阻力和阻力臂一定,动力臂最长越省力。
5.【分析】结合图片和生活经验,先判断杠杆在使用过程中,动力臂和阻力臂的大小关系,再判断它是属于哪种类型的杠杆。
【解答】解:
A、起子在使用过程中,动力臂大于阻力臂,是省力杠杆,但费距离;
B、道钉撬在使用过程中,动力臂大于阻力臂,是省力杠杆,但费距离;
C、筷子在使用过程中,动力臂小于阻力臂,是费力杠杆,可以省距离;
D、钢丝钳在使用过程中,动力臂大于阻力臂,是省力杠杆,但费距离。
故选:C。
【点评】此题考查的是杠杆的分类,主要包括以下几种:①省力杠杆,动力臂大于阻力臂;②费力杠杆,动力臂小于阻力臂;③等臂杠杆,动力臂等于阻力臂。
6.【分析】结合图片和生活经验,先判断杠杆在使用过程中,动力臂和阻力臂的大小关系,再判断它是属于哪种类型的杠杆;费力杠杆费力,但能省距离。
【解答】解:
①钓鱼竿在使用时,动力臂小于阻力臂,属于费力杠杆,但省距离;
②羊角锤在使用时,动力臂大于阻力臂,属于省力杠杆,但费距离;
③筷子在使用时,动力臂小于阻力臂,属于费力杠杆,但省距离;
④核桃夹在使用时,动力臂大于阻力臂,属于省力杠杆,但费距离。
所以,不能省力但能省距离的是①③。
故选:A。
【点评】杠杆的分类主要包括以下几种:①省力杠杆,动力臂大于阻力臂;②费力杠杆,动力臂小于阻力臂;③等臂杠杆,动力臂等于阻力臂。
7.【分析】由杠杆平衡条件F1L1=F2L2可知,在阻力和阻力臂都一定的情况下,动力臂越长则动力越小。所以要判断哪个动力最小,就看哪个动力对应的动力臂最长。支点与动力作用点之间的连线就是最长的动力臂,与这条动力臂垂直的力即为最小动力。当杠杆平衡时,动力和阻力使杠杆转动的方向是不同的,即相反。
【解答】解:
由图可知,动力F4、F2都与OA垂直,则动力F4和F2对应的动力臂就是OA,它是最长的动力臂;
由杠杆平衡条件F1L1=F2L2可知,在阻力和阻力臂都一定的情况下,动力臂越长则动力越小;因为F4和F2对应的动力臂最长,所以F4和F2最小;
为使杠杆平衡时,动力和阻力的转动效果是相反的,左边的阻力使杠杆有逆时针转动的效果,则右边的动力应有使杠杆顺时针转动的效果,即动力的方向应向下,所以可判断最小的力是F2。
故选:B。
【点评】本题考查杠杆平衡条件的应用,使用杠杆,当阻力和阻力臂一定时,动力臂越长越省力,找出最长的动力臂是本题的关键。同时要明确当杠杆平衡时,动力和阻力使杠杆转动的方向是不同的,即相反。
8.【分析】原来杠杆平衡,是因为两边的力和力臂的乘积相等,现在各减一个同样的钩码,就要看现在的力和力臂的乘积是否相等,据此分析得出结论。
【解答】解:
设一个钩码重为G,一个小格的长度为L,则左边力臂为2L,右边力臂为3L,
原来:3G×2L=2G×3L,杠杆处于水平平衡,
若把杠杆的两端各去掉一个钩码,
此时左边力与力臂的乘积2G×2L=4GL,右边力与力臂的乘积G×3L=3GL,
因4GL>3GL,所以杠杆不再水平平衡,杠杆左端下降,右端上升。
故选:C。
【点评】本题考查了杠杆平衡条件的应用,杠杆是否平衡取决于力和力臂的乘积是否相等,单独比较力或力臂大小不能得出正确结果。
9.【分析】根据杠杆原来平衡,设移动的距离为L,再比较F1(L1﹣L)和F2(L2﹣L)即可作出判断。
【解答】解:
原来平衡时,由杠杆的平衡条件可得F1?AO=F2?BO,
因为AO>BO,所以F1<F2;
设向支点O移动相同的距离为L,
则A端力与力臂的乘积为:F1(AO﹣L)=F1AO﹣F1L,
B端力与力臂的乘积为:F2(BO﹣L)=F2BO﹣F2L,
因F1<F2,则F1L<F2L,
所以F1(AO﹣L)>F2(BO﹣L),
则杠杆的A端向下倾斜;
故选:B。
【点评】用杠杆的平衡条件,判断出力与力臂乘积的变化值,从而判断出某些量的大小,也是杠杆知识的一种基本应用。
10.【分析】利用下列知识分析判断:
(1)支点:硬棒绕着转动的点叫支点;
(2)支点到力的作用线的距离叫力臂;
(3)对杠杆的分类方法:动力臂大于阻力臂的杠杆为省力杠杆;动力臂小于阻力臂的杠杆为费力杠杆;动力臂等于阻力臂的杠杆为等臂杠杆;
(4)定滑轮的作用,:改变力的方向,但不能省力。
【解答】解:
A、滑轮组C的轴固定不动,为定滑轮,定滑轮的作用是改变力的方向,而不能省力,故A错;
B、由图可知吊桥绕着B点转动,所以护城河上安装的吊桥的支点是B点,故B错;
CD、如图,支点B到力的作用线的距离BD为动力臂L1,
在匀速拉起吊桥时,拉力的作用点是A点,阻力的作用点是桥AB的中点,过支点B做阻力作用线的垂线得到的线段,即为阻力臂L2,比较两力臂的大小可知,它的动力臂大于阻力臂,所以属于一个省力杠杆;故C错、D正确。
故选:D。
【点评】解题本题要求学生知道支点及力臂的定义、定滑轮的作用,在解题时先找出支点的位置,然后根据力臂的定义判断动力臂与阻力臂的长短。
11.【分析】(1)杠杆分类:动力臂小于阻力臂的杠杆是费力杠杆;动力臂大于阻力臂的杠杆是省力杠杆;动力臂等于阻力臂的杠杆是等臂杠杆;
(2)根据内外气压的大小分析
【解答】解:
AB、用力压下手柄过程中,手柄的动力臂大于阻力臂,为省力杠杆,故AB错误;
CD、灭火器在使用的过程中,里面的气压大于外界的气压,干粉在压强差的作用下被喷出,故C错误、D正确。
故选:D。
【点评】本题利用考查了学生对杠杆分类方法、大气压强的了解与掌握,利用所学知识解释了有关灭火器的几个问题,体现了学以致用,有意义!
12.【分析】杠杆的五个要素:支点:杠杆绕着转动的点。
动力:使杠杆转动的力。动力臂:从支点到动力作用线的距离。
阻力:阻碍杠杆转动的力。阻力臂:从支点到阻力作用线的距离。
杠杆的平衡条件:动力×动力臂=阻力×阻力臂。
【解答】解:ABC、由图可见,杠杆绕O点转动,O为支点;作用在M点向下的是动力,是手对筷子的力FM,故B错误;作用在N点向上的力是阻力FN,故C正确;分别从支点O向阻力作用线作垂线,就得到阻力臂0N,用LN表示,动力臂是OM,故A错误;如下图:
D、把食物靠近支点放置时,阻力臂变小,根据杠杆的平衡条件可知食指对筷子上M点的压力FM变小,故D错误;
故选:C。
【点评】本题考查了力臂的画法和杠杆的平衡条件,画力臂的方法:首先确定支点、动力、阻力。然后用虚线画出动力和阻力的作用线,再做出支点力的作用线的距离,最后标出动力臂和阻力臂。
13.【分析】力臂是指从支点到力的作用线的距离,据此确定拉力F力臂。
【解答】解:
由图可知,O为支点,OB是从支点到拉力F的作用线的距离,所以OB是拉力F的力臂。
故选:A。
【点评】本题考查力臂的画法,记住:力臂是从支点到力的作用线的距离。
二.多选题(共3小题)
14.【分析】杠杆的分类和特点,主要包括以下几种:
①省力杠杆,动力臂大于阻力臂,省力但费距离;
②费力杠杆,动力臂小于阻力臂,费力但省距离;
③等臂杠杆,动力臂等于阻力臂,既不省距离也不省力。
【解答】解:苍蝇拍在使用过程中,阻力臂大于动力臂,故是费力杠杆,但能省距离。
故选:BC。
【点评】本题考查了生活中的物品和物理知识的联系,体现了物理来源于生活,服务于生活的宗旨,平时要养成多观察多思考的习惯,生活中处处有物理,每一件工具和物品都蕴含着丰富的物理知识。
15.【分析】结合图片和生活经验,判断杠杆在使用过程中,动力臂和阻力臂的大小关系,再判断它是属于哪种类型的杠杆。
【解答】解:①核桃夹在使用过程中,动力臂大于阻力臂,是省力杠杆;
②船桨在使用过程中,动力臂小于阻力臂,是费力杠杆;
③手推车在使用过程中,动力臂大于阻力臂,是省力杠杆;
④碗夹在使用过程中,动力臂小于阻力臂,是费力杠杆;
属于费力杠杆的是②④。
故选:BD。
【点评】本题考查的是杠杆的分类,主要包括以下几种:①省力杠杆,动力臂大于阻力臂;②费力杠杆,动力臂小于阻力臂;③等臂杠杆,动力臂等于阻力臂。
16.【分析】(1)杠杆的分类:①省力杠杆,动力臂大于阻力臂;②费力杠杆,动力臂小于阻力臂;③等臂杠杆,动力臂等于阻力臂。
(2)要使杠杆平衡,作用在杠杆上的两个力(用力点、支点和阻力点)的大小跟它们的力臂成反比。
【解答】解:(1)由图可见,桔槔是不等臂杠杆,动力臂大于阻力臂,是省力杠杆,故AC不正确,符合题意;
(2)向井内放送水桶时,人用的力通过杠杆原理,与石头的重力相关,一般比木桶的重力要大,故B说法不正确,符合题意;
(3)往上提水时,因为有石头帮忙,人的力气比水和桶的总重力小,故D选项说法正确,不符合题意。
故选:ABC。
【点评】本题考查了杠杆的应用,属于基础知识的考查,注重了物理知识和生活实际的联系。
三.填空题(共10小题)
17.【分析】(1)力的三要素有:力的大小、方向、作用点,它们都影响力的作用效果。
(2)结合图片和生活经验,先判断杠杆在使用过程中,动力臂和阻力臂的大小关系,再判断它是属于哪种类型的杠杆。
【解答】解:
(1)由图可看出,力的大小和方向相同,作用点A、B不同,在B点比A点更易夹碎核桃,说明力的作用效果与作用点有关。
(2)在使用核桃夹时,动力臂大于阻力臂,是省力杠杆。
故答案为:作用点;省力。
【点评】本题考查了力的作用效果、杠杆的分类,属于基础题目。
18.【分析】知道“给我一根杠杆和支点,我就能撬动地球”是古希腊学者阿基米德的一句豪言壮语。
【解答】解:
“给我一个支点,我就能撬动地球”是古希腊学者阿基米德的一句豪言壮语;阿基米德总结出的杠杆平衡条件,也被称为杠杆原理;
故答案为:阿基米德;杠杆。
【点评】本题考查了物理规律及其对应的科学家,考查的是物理学史,属于基础知识,平时在学习过程中应加强记忆。
19.【分析】结合图片,先确定支点,再根据动力臂和阻力臂的大小关系判断它是属于哪种类型的杠杆。
由杠杆的平衡条件可知,在阻力和阻力臂不变的情况下,动力臂越长越省力。
【解答】解:
由图知,撬棒在使用过程中,绕B点转动,则B点为支点,并且动力臂大于阻力臂,是省力杠杆。
由杠杆的平衡条件可知,在阻力和阻力臂不变的情况下,动力臂越长越省力;所以,在用力方向不变的情况下该人想用更小的力撬起石头,那么他的手应该向远离支点O方向移动,这样动力臂变长了,就越省力。
故答案为:B;省力;远离。
【点评】此题考查的是杠杆的分类和特点,主要包括以下几种:①省力杠杆,动力臂大于阻力臂,省力但费距离;②费力杠杆,动力臂小于阻力臂,费力但省距离;③等臂杠杆,动力臂等于阻力臂,既不省距离也不省力。
同时还考查了学生用杠杆的平衡条件分析问题的能力。
20.【分析】力臂是从支点到力的作用线的距离,由支点向力的作用线做垂线,垂线段的长度即为力臂。根据杠杆的平衡条件分析力F的变化。
【解答】解:
由图可知,AB是力F的作用线,OA⊥AB,OA为支点到力F的作用线的距离,所以线段OA表示力F的力臂。
如果拉力一直保持水平方向拉至杠杆到竖直方向,在拉动过程中,重力的力臂减小,如图:
;
根据杠杆平衡条件可知,拉力F的大小将变小。
故答案为:OA;变小。
【点评】本题考查了杠杆的相关知识,考生需要根据力臂的定义在图中识别出已知力F的力臂。引导教学要注重基本概念的理解和落实。
21.【分析】结合生活经验,要判断杠杆的类型,可依据杠杆的动力臂和阻力臂大小关系:若动力臂大于阻力臂,则是省力杠杆;若动力臂小于阻力臂,则是费力杠杆;若动力臂等于阻力臂,则为等臂杠杆。
【解答】解:
我们在使用①切纸刀、②钢丝钳时,都是动力臂大于阻力臂,都是为了省力,所以它们都是省力杠杆;
我们在使用③镊子、⑤食品钳时,都是动力臂小于阻力臂,所以它们都是费力杠杆;
④从摩天轮自身处于平衡时来分析,左右两侧物体的重力分别为动力和阻力,支点在圆心处,可以构成一个等臂杠杆。
故答案为:①②;③⑤;④。
【点评】该题考查了学生对物理模型的抽象、分析能力。判断杠杆的类型可结合生活经验和动力臂与阻力臂的大小关系来判断。注意天平是典型的等臂杠杆。
22.【分析】(1)抬起木材一端时,以另一端为支点;利用杠杆平衡条件:动力×动力臂=阻力×阻力臂可解答此题;
(2)求出将它竖直起来时木材的重心离水平面的高度,即为重心上升的高度,最后根据W=Gh求出需要做的功。
【解答】解:
(1)已知木材质量为1.2kg,则其重力G=mg=1.2kg×10N/kg=12N,
设其长度为L;抬起一端时,以另一端为支点,其重心到支点的距离为L,动力臂为L,
根据杠杆平衡条件则有:F×L=G×L;
解得F=G=×12N=6N,即至少要用6N的力;
(2)将它竖直起来时,木材的重心离水平面的高度为h===0.4m,
则至少需要做的功:W=Gh=12N×0.4m=4.8J。
故答案为:6;4.8。
【点评】知道杠杆平衡的条件,会熟练应用杠杆平衡的条件计算相关的力和力臂以及功的计算公式的掌握和应用,明确克服重力做功就是所需要做的功,求重心上升的高度是本题的易错点,要求学生要认真分析。
23.【分析】该题考查了学生对物理模型的抽象、分析能力。判断杠杆的类型可结合生活经验和动力臂与阻力臂的大小关系来判断。常见的等臂杠杆有天平、跷跷板、定滑轮。
【解答】解:我们使用①剪铁皮的剪刀、⑥羊角锤、⑦老虎钳都是为了省力,并且在使用的过程中都是动力臂大于阻力臂,所以它们都是省力杠杆;
我们使用③筷子、⑤镊子、⑧钓鱼竿都是为了省距离,并且在使用的过程中都是动力臂小于阻力臂,所以它们都是费力杠杆;
天平是典型的等臂杠杆,它的动力臂等于阻力臂;
在使用定滑轮时既不省力也不省距离,它实质上是一个等臂杠杆。
故答案为:①⑥⑦;③⑤⑧;②④。
【点评】本题考查了杠杆、滑轮的分类和使用特点。省力杠杆省力但费距离,费力杠杆费力但省距离,等臂杠杆不省力也不省距离。既省力又省距离的机械是不存在的。
24.【分析】结合图片和生活经验,先判断船桨在使用过程中,动力臂和阻力臂的大小关系,再判断它是属于哪种类型的杠杆,进而确定是省距离还是费距离。
【解答】解:
因为船桨在使用过程中,动力臂小于阻力臂,所以船桨属于费力杠杆,但省距离,这样运动员的手移动很小的距离时,可使船桨在水中划过的距离很大,从而加快了赛艇前进的速度。
故答案为:费力;大于。
【点评】本题考查了杠杆的分类和特点,属于基本内容,比较简单。
25.【分析】根据杠杆原理进行分析,在力一定的情况下,分析力臂的大小关系,力臂的越大越容易被大风吹倒。
【解答】解:我们可以把树看作一个杠杆模型,支点为树根处,当都受到同样大小的风力作用时,树越高,其力臂越大,越容易被风吹倒。
故答案为:杠杆;乙。
【点评】本题考查杠杆平衡条件的应用,力与力臂的乘积越大,其作用效果越大。
26.【分析】气球膨胀后气球和篮球的总体积增大,根据阿基米德原理判断它们所受浮力的变化;再根据F拉=G总﹣F浮判断杠杆左端产生拉力的变化,最后根据杠杆的平衡条件判断杠杆的平衡情况。
【解答】解:因为杠杆原来是平衡的,
所以:G总×l1=G码×l2;
气球膨胀后,气球和篮球的总体积增大,
根据公式F浮=ρ气gV排得到,它们受到的浮力F浮增大;
根据F拉=G总﹣F浮可知,总重力G总不变,气球和篮球对杠杆的拉F拉变小;
因为杠杆的动力臂l1、阻力臂l2和阻力G码(钩码重力)保持不变,
根据杠杆的平衡条件得到:F拉×l1<G码×l2;
那么杠杆的左端向上翘起,这是因为浮力增大的缘故。
故答案为:左;浮力增大。
【点评】知道影响浮力大小的因素,能够正确的进行受力分析是解决本题的关键。
四.作图题(共7小题)
27.【分析】(1)根据重力的方向是竖直向下的,过重心做竖直向下的力即可。
(2)杠杆平衡条件:动力×动力臂=阻力×阻力臂(F1L1=F2L2),在阻力跟阻力臂的乘积一定时,动力臂越长,动力越小。
【解答】解:重力的方向是竖直向下的,过物体重心画一条带箭头的竖直向下的有向线段,用G表示;
由杠杆平衡条件F1L1=F2L2可知,在阻力跟阻力臂的乘积一定时,动力臂越长,动力越小;图中支点在O点,左端距离支点最远,因此OA作为动力臂时最长,此时动力最小,由图知动力的方向应该垂直于OA向上,如下图所示:
【点评】本题主要考查了重力示意图的画法和杠杆中最小力的问题。解决此类题目的关键是确定出最长的力臂,并根据力臂的画法做出最小的力。
28.【分析】力臂是支点到力的作用线的距离,作图时把握住力和力臂的垂直关系即可做出动力。
【解答】解:过力臂L1的末端,作垂直于L1的直线,与杠杆的交点为力F1的作用点,为使杠杆平衡,力F1的方向应向上,据此画出力F1的示意图,如图所示:
【点评】本题考查了力臂的画法。知道力臂是从支点到力的作用线的垂直距离是关键,易错点将垂足当做动力作用点。
29.【分析】力臂的画法:首先确定支点O;然后延长动力的作用线(用虚线);再由支点向动力作用线做垂线(用虚线);用双箭头标出L1.先确定阻力作用点(即B点),然后过阻力作用点表示阻力的方向(即竖直向小);
【解答】解:从支点O作动力F作用线的垂线段,垂线段的长度即为动力臂L1;
阻力作用点在点B,方向竖直向下,如图所示:
【点评】明确力臂的概念,从支点向力的作用线画垂线,即可找出力臂的位置,阻力是阻碍杠杆转动的力,明确了这些基本概念便不难解决。
30.【分析】已知支点,画出动力作用线,过支点作垂直于力的作用线的垂线段,可得力臂。
【解答】解:
过支点O作垂直于动力作用线的垂线段,可得动力臂L1,如图所示;
【点评】本题考查了力臂的画法,属于基础题目。
31.【分析】支点到作用线的距离为力臂;过动力臂的末端作一条垂直于力臂的直线,可得动力作用线,进而画出动力F1。
【解答】解:
过力臂L1的末端作一条垂直于力臂的直线即为动力F1的作用线,与杠杆的交点A为动力作用点,为使杠杆平衡,动力的方向应斜向下,据此作出F1的示意图;
过支点O作垂直于阻力F2作用线的垂线段,即为阻力臂L2,如图所示:
【点评】知道杠杆中力与力臂的关系,会根据力臂的画法作出杠杆的作用力或力臂。
32.【分析】先画出力F1的作用线,然后过支点作F1作用线的垂线段,可得其力臂。
【解答】解:
反向延长F1画出F1的作用线,过支点O作F1作用线的垂线段,即为F1的力臂L1,如图所示:
【点评】本题考查了力臂的画法。画力臂时关键是要画出支点到力的作用线的垂线段。
33.【分析】已知动力和阻力,根据力臂的画法,先确定支点O,再过支点作动力作用线和阻力作用线的垂线段,即可画出动力臂和阻力臂。
【解答】解:已知支点为O,延长F2画出力的作用线,过支点O作力F2作用线的垂线段L2,过支点O作力F1作用线的垂线段L1,则L1、L2即为所求作的力臂。如图所示:
【点评】力臂的画法:①首先根据杠杆的示意图,确定杠杆的支点。②确定力的作用点和力的方向,画出力的作用线。③从支点向力的作用线作垂线,支点到垂足的距离就是力臂。
五.实验探究题(共2小题)
34.【分析】(1)杠杆倾斜时,杠杆的重心偏向杠杆下沉的一端,左、右两端的螺母(或一端的螺母)要向杠杆上翘的一端调节;实验前先要调节杠杆在水平位置平衡,这是为使杠杆所受的重力通过支点,从而可以不考虑杠杆的重力对其转动的影响;
(2)若采用弹簧测力计,拉力的方向由竖直向下逐渐向右倾斜时,判断出动力臂的变化,根据杠杆平衡原理即可判断动力大小;
(3)杠杆的重心过支点,可以消除杠杆重对杠杆平衡的影响。
(4)杠杆在水平位置平衡时,力的方向与杠杆垂直,力臂的长度可以直接从杠杆上读出来。
【解答】解:(1)将杠杆中点置于支架上,当杠杆静止时,发现杠杆右端下沉,左端上翘,平衡螺母向上翘的左端移动,即把杠杆左端的平衡螺母向左调节,直到杠杆在不挂钩码时,保持水平位置静止状态;
(2)杠杆平衡后,若在A点挂4个钩码,则左边点重力为4G,
又因为力臂OA=3,左边力臂OB=2,
实验由杠杆的平衡条件(F1l1=F2l2)可知:4G×3=F1×2,实验F1=6G;故应在B点应挂6个钩码,才能使杠杆恢复平衡;
若采用弹簧测力计,拉力的方向由竖直向下逐渐向右倾斜时,动力臂变小了,根据杠杆平衡条件可知:弹簧测力计的示数将变大了。
(3)如图乙示装置进行探究,杠杆的重心没有通过支点,杠杆的重对杠杆平衡有影响
(4)杠杆处于静止状态或匀速转动状态都叫杠杆平衡,所以小海的说法是对的;
力臂等于支点到力的作用线的距离,在小红的实验方案中,当杠杆在水平位置平衡时,力的方向与杠杆垂直,力臂可以从杠杆标尺刻度上直接读出来。而甲实验方案中的力臂不便于测量,所以,小红的实验方案好。
故答案为:
(1)左;水平;
(2)6;变大;动力臂变小了;
(3)杠杆自身的重力;
(4)对;小红; 便于测量力臂。
【点评】探究杠杆平衡条件时,使杠杆在水平位置平衡,便于测量力臂大小,杠杆的重心通过支点,消除杠杆重对杠杆平衡的影响,使实验简单化,便于探究。
35.【分析】(1)在调平杠杆平衡时,杠杆的哪端高,平衡螺母要向哪端移动;
(2)①根据杠杆的平衡条件计算出在B点挂的钩码个数或拉力的大小;使杠杆平衡在水平位置的目的是便于测量力臂;
②当拉力F向右倾斜时,分析出力臂的变化结合杠杆的平衡条件判断力的变化;
(3)根据杠杆的平衡条件分析即可。
【解答】解:(1)杠杆静止时,杠杆左端下沉,说明右端偏高,平衡螺母需向右调节;
(2)①设杠杆每个格的长度为L,每个钩码的重力为G,根据杠杆的平衡条件:
FALA=FBLB,即2G×3L=FB×2L,解得FB=3G,需挂3个钩码。
使杠杆平衡在水平位置的目的是便于测量力臂;
②若拉力F向右倾斜时,此时F的力臂变短,根据杠杆的平衡条件,力变大;
(3)若不计杠杆的重力,根据杠杆的平衡条件:
F向上L向上=F向下L向下
F′?4L=3G?8L
解得F′=6G=6×0.5N=3N,
实验中发现弹簧测力计的示数为3.5N,数据不符合杠杆平衡条件,原因是杠杆自身有重力。
故答案为:(1)右;(2)①3;便于测量力臂;②变大;F的力臂变短;(3)杠杆自身有重力。
【点评】此题是探究杠杆平衡实验,考查了杠杆的调平及杠杆平衡条件的应用,在利用平衡条件公式时,要注意分析力和对应的力臂。
六.计算题(共3小题)
36.【分析】确定独轮车的支点,然后找出动力臂和阻力臂,动力和阻力,根据杠杆的平衡条件进行计算。
【解答】解:(1)独轮车的车辆轮轴处是支点,其中重力G是阻力,支点到重力作用线的距离是阻力臂,故阻力臂是0.4m;
力F1是动力,支点到力F作用线的距离是动力臂,故动力臂是0.4m+1.2m=1.6m;
(2)由杠杆的平衡条件可知:F1×L动=G×L阻,得F1===250N。
答:(1)F1的力臂l1的大小是1.6m;
(2)F1的大小是250N。
【点评】此题考查了杠杆平衡条件的应用,要掌握杠杆的平衡条件,确定杠杆受到的力及对应的力臂,根据杠杆的平衡条件进行求解。
37.【分析】图中O为支点,OA为重力的力臂,OB为拉力的力臂,根据杠杆平衡条件可求出在B点挂的物体的重力大小,然后即可求出质量。
【解答】解:
由题可知,F1=196N,拉力的力臂OA=OB+AB=0.3cm+0.9cm=1.2m,重力的力臂OB=30cm=0.3m;
根据杠杆平衡条件可得:F1×OA=G×OB,
则G===7845N,
所以质量m===80kg。
答:B点能挂的物体质量最大为80kg。
【点评】本题考查了杠杆平衡条件的应用,关键是要找准力臂,计算时要注意力与力臂的对应。
38.【分析】杠杆水平平衡,先求出动力臂、阻力臂、阻力,再利用杠杆平衡条件求细绳的拉力。
【解答】解:
如下图所示,由于杠杆水平平衡,在Rt△OBA中,∠OAB=30°,则OB=×OA=×10cm=5cm,即动力臂为OB等于5cm,阻力臂为OC等于10cm,
杠杆受到的阻力F阻=G球=m球g=5kg×10N/kg=50N,
由杠杆平衡条件可得:F×OB=F阻×OC,
即:F×5cm=50N×10cm,
解得:F=100N。
答:细绳的拉力为100N。
【点评】本题考查了重力公式和杠杆平衡条件的应用,利用直角三角形的角边关系求出动力臂大小是关键。
七.解答题(共2小题)
39.【分析】如图,假设支点为O,知道杠杆两端受力的大小,找出两边力的力臂,根据杠杆平衡条件求解;若杠杆两端所挂重物各增加50N,假设支点为O′,知道杠杆两端受力的大小,找出两边力的力臂,根据杠杆平衡条件求解。
【解答】解:
如图,O为支点,
F1=200N,F2=50N,
因为杠杆平衡,
所以F1LOB=F2(Lm﹣LOB),
即:200N×LOB=50N×(1m﹣LOB),
所以LOB=0.2m。
同理,若杠杆两端所挂重物各增加50N,假设支点为O′,
F2′=50N+50N=100N;F1′=200N+50N=250N,
F1′LOB′=F2′(Lm﹣LOB′),
250N×LOB′=100N×(1m﹣LOB′),
解得LOB′=0.285m。
答:(1)支点应距B物体那端0.2米时,杠杆才能平衡;(2)若杠杆两端所挂重物各增加50N,支点应距左端0.285m才能使杠杆平衡。
【点评】本题考查了学生对杠杆平衡条件的掌握和运用,因为支点待确定,有难度,最好画出杠杆示意图帮助理清思路。
40.【分析】(1)根据题意对扁担进行受力分析;
(2)以扁担的左端点为支点,确定动力臂和阻力臂的大小,由杠杆平衡条件求出乙对扁担的力,
根据力的作用是相互的求出扁担对乙的压力;
(3)以扁担的右端点为支点,确定动力臂和阻力臂的大小,由杠杆平衡条件求出甲对扁担的力,
根据力的作用是相互的求出扁担对甲的压力。
【解答】解:扁担受力如图所示;
以扁担的左端点为支点,由杠杆平衡条件:动力×动力臂=阻力×阻力臂,
答:两人肩上各担200N,120N的力。
【点评】本题考查了力的平衡条件与杠杆平衡条件的应用,根据题意作出图示,使物理情景直观、明了,有助于解题。
声明:试题
基础练习
一.选择题(共13小题)
1.“给我一个支点和一根足够长的棍,我就能撬起整个地球。”如图所示,生产和生活中的杠杆与阿基米德设想的杠杆属于同一类型的是( )
2.四种剪刀中,最适用于剪开铁皮的是( )
3.如图表示出了人的前臂曲肘时的情况,并标出了支点的位置。当手握重物时,肌肉受到的拉力约是物重的8倍。由此可看出人的这一肌肉杠杆属于( )
A.费力杠杆 B.省力杠杆
C.不省力也不省距离的杠杆 D.既省力又可省距离杠杆
4.如图所示,质量忽略不计的AC硬棒能绕O点转动,在B点挂一物体。在C点施加力F1时,棒刚好处于静止状态。下列说法中正确的是( )
A.此时,F1 的方向向上
B.在C点无论向哪个方向拉,F1大小不变
C.这是一个费力杠杆
D.F1=F2
5.下列工具在正常使用的过程中,可以省距离的是( )
6.如图所示的四种工具中,使用时不能省力但能省距离的是( )
A.①③ B.②③ C.①④ D.②④
7.如图所示,O为杠杆AB的支点,B点挂一重物G,为了使杠杆在水平位置平衡,现在在A点施加一个拉力,以下四个力中最小的是( )
A.F1 B.F2 C.F3 D.F4
8.如图所示的杠杆正处于水平平衡,若把杠杆的两端钩码各去一个,杠杆将( )
A.还继续处于水平平衡
B.右端下降,左端上升
C.右端上升,左端下降
D.无法确定杠杆的运动状态
9.如图所示的杠杆平衡,若F1、F2的大小和方向均不变,它们的作用点同时向支点0移动相同的距离,则( )
A.杠杆仍平衡 B.A端下倾 C.B端下倾 D.无法确定
10.在我国古代,简单机械就有了许多巧妙的应用,护城河上安装的吊桥装置就是一个例子,如图所示。在拉起吊桥过程中( )
A.滑轮起到省力的作用 B.A点是吊桥的支点
C.AB是吊桥的阻力臂 D.吊桥是省力杠杆
11.为了消防安全,楼历每层必须配备灭火器。下列关于图示灭火器的说法正确的是( )
A.用力压下手柄过程中,手柄相当于一个等臂杠杆
B.用力压下手柄过程中,手柄相当于一个费力杠杆
C.干粉能喷出是因为灭火器内的气压等于外界大气压
D.干粉能喷出是因为灭火器内的气压大于外界大气压
12.筷子是东亚文化圈普遍使用的餐具,如图所示将AB这支筷子作为杠杆分,O点为支点,食指指头对筷子上M点的压力FM(垂直于筷子)是动力。则( )
A.阻力臂是MN、动力臂是OM
B.阻力是筷子对食物的压力
C.阻力的方向向上
D.把食物靠近支点放置时,食指对筷子上M点的压力FM变大
13.如图所示的杠杆OC中,拉力F的力臂为( )
A.OB B.OA
C.OC D.BC
二.多选题(共3小题)
14.使用苍蝇拍时,以迅雷不及掩耳之势,轻易拍到苍蝇,这是利用了杠杆的哪个特点( )
A.省力 B.费力 C.省距离 D.费距离
15.在图中,所使用的杠杆属于费力杠杆的是( )
A.① B.② C.③ D.④
16.在我国古代书籍《墨经》中,对杠杆有精辟论述,并有许多巧妙的应用。如图所示是在井上汲水的桔槔,下列对其在使用中不正确的解释是( )
A.桔槔是等臂杠杆,不省力也不费力
B.向井内放送水桶时,人用的力气一定小于水桶的重力,所以省力
C.桔槔是不等臂杠杆,动力臂小于阻力臂,是费力杠杆
D.往上提水时,人用的力气一定小于桶与水的总重,所以省力
三.填空题(共10小题)
17.如图1所示为一种常用核桃夹,用大小相同的力垂直作用在B点比A点更容易夹碎核桃,这说明力的作用效果与 有关。核桃夹是 杠杆。
18.如图2,古希腊学者 最早总结出杠杆平衡条件也称 原理,并说出这样一句豪言壮语:只要给我一个支点,我就可以移动地球。
19.如图3,在用杠杠撬石头的过程中,支点在图中的 点,该杠杆属于 杠杆,在用力方向不变的情况下该人想用更小的力撬起石头,那么他的手应该向 支点的方向移动(选填“远离”或“靠近”)。
20.如图4所示,OB是以O点为支点的杠杆,F是作用在杠杆B端的力。图中线段AB与力F的作用线在一条直线上,且OA⊥AB.线段 (OA/AB/OB)表示力F的力臂,如果拉力一直保持水平方向拉至杠杆到竖直方向,拉力F大小将 (变小/不变/变大)。
21.生活中杠杆的应用十分广泛,比如:①切纸刀②钢丝钳③镊子④摩天轮⑤食品钳。其中属于省力杠杆的有 ,属于费力杠杆有 ,属于等臂杠杆有 。
22.一根水平放置、粗细均匀的木材长0.8m,质量为1.2kg:若将它缓慢竖立起来(如图5所示),至少需要 N的力,需要做的功为 J.(g=10N/kg)
23.在下列工具中:①剪铁皮的剪刀 ②托盘天平 ③筷子 ④定滑轮 ⑤镊子 ⑥羊角锤 ⑦老虎钳 ⑧钓鱼竿,属于省力杠杆的有 ,属于费力杠杆的有 ,属于等臂杠杆的有 。(填序号,漏选错选均不得分)
24.如图6所示,人在划船时,船桨属于 杠杆。船桨在水中移动的距离 手移动的距离,从而加快船前进的速度。
25.如图7所示的甲、乙两棵树,它们的树冠和根系基本相同,只是乙比甲高。当我们研究哪棵树容易被大风吹倒或折断时,可以把树看作是一个 模型,由此可以判断出 树容易被吹倒或折断。
26.将充足气的篮球和套扎在气针尾端的气球一起挂于杠杆左端,调整杠杆右端钩码的悬挂位置,使杠杆平衡(如图8),然后再将扎在气球上的气针头插入篮球的气门内,气球随即膨胀。此时的杠杆的 端将向上翘起,这是因为 的缘故。
四.作图题(共7小题)
27.在图9中画出物体的重力和使杠杆在图示位置平衡的最小力
28.如图10所示杠杆在力F1、F2的作用下静止,请根据力臂L1画出力F1。
29.如图11中活塞抽水机的柄是一根弯曲的杠杆,请画出动力F的力臂L1及阻力F2的示意图。
30.如图12所示,用螺丝刀撬起图钉。请在图上画出螺丝刀受到动力F1的力臂;
31.如图13,杠杆处于平衡状态,请根据力臂画出动力F1和阻力F2的力臂L2。
32.图14是利用杠杆吊起重物的情景,O是支点,请画出F1的力臂,并用字母L1表示。
33.如图15所示,杠杆中O为支点,请画出:
①F1的力臂; ②F2的力臂。
五.实验探究题(共2小题)
34.如图16所示,在探究“杠杆的平衡条件”实验中用到的实验器材有:杠杆、铁架台、弹簧测力计、刻度尺、细线和质量相同的钩码若干个。
(1)实验前,将杠杆中点置于支架上,当杠杆静止时,发现杠杆右端下沉。此时,应把杠杆左端的平衡螺母向 (选填“左”或“右”)调节,使杠杆在不挂钩码时,保持在 位置并静止。
(2)杠杆调节平衡后,小明在杠杆上A点处挂4个钩码(如图甲所示),为了使杠杆仍在水平位置平衡,可以在B点处挂 个钩码或用弹簧测力计拉杠杆。若采用弹簧测力计,拉力的方向由竖直向下逐渐向右倾斜时,为使杠杆仍然保持平衡,弹簧测力计的示数将 (选填“变大”、“变小”或“不变”),其原因是 。
(3)实验结束后,小明提出了新的探究问题:“若支点不在杠杆的中点时,杠杆的平衡条件是否仍然成立?”于是小明同学利用如图乙所示装置进行探究,发现在杠杆左端的不同位置,用弹簧测力计竖直向上拉使杠杆处于水平平衡时,测出的拉力大小都与杠杆平衡条件不相符,其原因可能是 对实验产生了影响。
(4)关于“杠杆不处于水平位置能否平衡?”小海和小红意见不同。小海认为能平衡,于是他每次让杠杆倾斜到同一位置静止,这样实验也得出了同样的杠杆平衡条件。小海认为杠杆平衡不一定是水平的,这种说法对吗? (填“对”或“错”),小海这种方案与小红让杠杆在水平位置做实验的方案相比较,你认为小海和小红哪位同学的实验方案好?请说明理由:答: 的实验方案好;理由是 。
35.小王利用杠杆进行探究“杠杆的平衡条件”的实验。(每个钩码重0N)
(1)实验前,将杠杆的中点置于支架上,当杠杆静止时,发现杠杆左端下沉,这时应将平衡螺母向 (选填“左”或“右”)端调节,直到杠杆在水平位置平衡;
(2)如图甲所示,①在杠杆A点处挂2个钩码,则在B点处应挂 个同样的钩码,杠杆仍然在水平位置平衡,实验中使杠杆平衡在水平位置的目的是 。
②把B点处的钩码取下,弹簧测力计在B点处施加一个竖直向下的拉力F,杠杆仍在水平位置平衡。当拉力F向右倾斜时,仍要保持杠杆水平平衡,拉力F的大小将 (选填“变大”、“变小”或“不变”),原因是 。
(3)小王对器材进行了改装,又做了如图乙所示的探究,用弹簧测力计在C点竖直向上拉,使杠杆仍然处于水平位置平衡,实验中发现弹簧测力计的示数为3.5N,数据不符合杠杆平衡条件,原因是 。
六.计算题(共3小题)
36.如图所示是搬运泥土的独轮车,设车子和泥土的总重G=1000N,运泥土时从A点竖直提起独轮车把手的力是F1.则:
(1)F1的力臂l1的大小是多少?
(2)F1的大小是多少?
37.如图所示,有一轻质杠杆OA,OB长30厘米,AB长0.9米,A端绳子承受到向上的最大拉力为196牛,要使杠杆水平平衡,B点能挂的物体质量最大为?
38.如图所示的杠杆在细绳的拉力作用下在水平处于平衡状态,已知小球的质量是5kg,放在距离支点10cm处,A点到支点的距离是10cm,求细绳的拉力。(g=10N/kg)
七.解答题(共2小题)
39.有一根杠杆,长度为1m,挂在其一端的物体重为50N,挂在另一端的物体为200N,问:
(1)支点应距左端多远才能使杠杆平衡?
(2)若杠杆两端所挂重物各增加50N,支点应距左端多远才能使杠杆平衡?
40.在学校开展“感恩教育活动”之际,九年级(1)班的大李和小李为敬老院送去一袋重320N的大米,如图所示,扁担长1.6m,O点距大李0.6m,问两人肩上各担多大的力?(不计扁担重)
沪科版物理八年级第十章机械与人第一节 科学探究:杠杆的平衡条件
基础练习参考答案与试题解析
一.选择题(共13小题)
【点评】此题考查的是杠杆的分类,主要包括以下几种:①省力杠杆,动力臂大于阻力臂;②费力杠杆,动力臂小于阻力臂;③等臂杠杆,动力臂等于阻力臂。
2.【分析】结合生活经验和图片,先判断剪刀在使用过程中的目的,再根据各类杠杆的特点选择所需要的剪刀。
【解答】解:
剪开较硬的物体,就需要一把省力的剪刀,因此需选用动力臂大于阻力臂的剪刀,即手柄比刀口长的剪刀,所以D最适合。
故选:D。
【点评】剪刀是生活中一种特殊杠杆,要根据需要选择最合适的。手柄长的剪刀省力,刀口长的剪刀省距离。
3.【分析】要判断杠杆的类型,可依据杠杆的动力臂和阻力臂的大小关系:若动力臂大于阻力臂,是省力杠杆;若动力臂小于阻力臂,是费力杠杆;若动力臂等于阻力臂,则为等臂杠杆。
【解答】解:人的前臂可视为杠杆,当曲肘将茶杯向上举起,支点在下端,此时动力臂小于阻力臂,并且肌肉受到的拉力约是物重的8倍,人的这一肌肉杠杆属于费力杠杆,费力杠杆省距离,故A正确、BCD错。
故选:A。
【点评】本题考查了学生对物理模型的抽象、分析能力。判断杠杆的类型可根据生活经验结合动力臂与阻力臂的大小关系来判断。
4.【分析】(1)由图知,杠杆支点在O,阻力作用在B点,方向向下,为使杠杆静止(处于平衡状态),在C点施加力时,力 的方向需要向上;
(2)由(1)知动力 的方向向上,当垂直于杠杆向上时,动力臂最长,而阻力和阻力臂一定,由杠杆平衡条件可知,此时动力最小;
(3)由于动力臂的大小不能确定,无法得出动力臂和阻力臂的大小关系,无法确定是费力杠杆还是省力杠杆。
【解答】解:
A、如图,杠杆支点在O,阻力作用在B点,方向向下,为使杠杆静止(处于平衡状态),在C点施加力F1时,F1 的方向需要向上,故A正确;
B、F1 的方向向上,当垂直于杠杆向上时,动力臂最长,而阻力和阻力臂一定,由杠杆平衡条件可知,此时动力最小;当动力方向不是垂直于杠杆时,动力变大,故B错;
CD、由于动力臂的大小不能确定,无法得出动力臂和阻力臂的大小关系,无法确定是费力杠杆还是省力杠杆,动力不一定等于阻力,故CD错。
故选:A。
【点评】本题考查了杠杆平衡条件的应用,注意:在阻力和阻力臂一定,动力臂最长越省力。
5.【分析】结合图片和生活经验,先判断杠杆在使用过程中,动力臂和阻力臂的大小关系,再判断它是属于哪种类型的杠杆。
【解答】解:
A、起子在使用过程中,动力臂大于阻力臂,是省力杠杆,但费距离;
B、道钉撬在使用过程中,动力臂大于阻力臂,是省力杠杆,但费距离;
C、筷子在使用过程中,动力臂小于阻力臂,是费力杠杆,可以省距离;
D、钢丝钳在使用过程中,动力臂大于阻力臂,是省力杠杆,但费距离。
故选:C。
【点评】此题考查的是杠杆的分类,主要包括以下几种:①省力杠杆,动力臂大于阻力臂;②费力杠杆,动力臂小于阻力臂;③等臂杠杆,动力臂等于阻力臂。
6.【分析】结合图片和生活经验,先判断杠杆在使用过程中,动力臂和阻力臂的大小关系,再判断它是属于哪种类型的杠杆;费力杠杆费力,但能省距离。
【解答】解:
①钓鱼竿在使用时,动力臂小于阻力臂,属于费力杠杆,但省距离;
②羊角锤在使用时,动力臂大于阻力臂,属于省力杠杆,但费距离;
③筷子在使用时,动力臂小于阻力臂,属于费力杠杆,但省距离;
④核桃夹在使用时,动力臂大于阻力臂,属于省力杠杆,但费距离。
所以,不能省力但能省距离的是①③。
故选:A。
【点评】杠杆的分类主要包括以下几种:①省力杠杆,动力臂大于阻力臂;②费力杠杆,动力臂小于阻力臂;③等臂杠杆,动力臂等于阻力臂。
7.【分析】由杠杆平衡条件F1L1=F2L2可知,在阻力和阻力臂都一定的情况下,动力臂越长则动力越小。所以要判断哪个动力最小,就看哪个动力对应的动力臂最长。支点与动力作用点之间的连线就是最长的动力臂,与这条动力臂垂直的力即为最小动力。当杠杆平衡时,动力和阻力使杠杆转动的方向是不同的,即相反。
【解答】解:
由图可知,动力F4、F2都与OA垂直,则动力F4和F2对应的动力臂就是OA,它是最长的动力臂;
由杠杆平衡条件F1L1=F2L2可知,在阻力和阻力臂都一定的情况下,动力臂越长则动力越小;因为F4和F2对应的动力臂最长,所以F4和F2最小;
为使杠杆平衡时,动力和阻力的转动效果是相反的,左边的阻力使杠杆有逆时针转动的效果,则右边的动力应有使杠杆顺时针转动的效果,即动力的方向应向下,所以可判断最小的力是F2。
故选:B。
【点评】本题考查杠杆平衡条件的应用,使用杠杆,当阻力和阻力臂一定时,动力臂越长越省力,找出最长的动力臂是本题的关键。同时要明确当杠杆平衡时,动力和阻力使杠杆转动的方向是不同的,即相反。
8.【分析】原来杠杆平衡,是因为两边的力和力臂的乘积相等,现在各减一个同样的钩码,就要看现在的力和力臂的乘积是否相等,据此分析得出结论。
【解答】解:
设一个钩码重为G,一个小格的长度为L,则左边力臂为2L,右边力臂为3L,
原来:3G×2L=2G×3L,杠杆处于水平平衡,
若把杠杆的两端各去掉一个钩码,
此时左边力与力臂的乘积2G×2L=4GL,右边力与力臂的乘积G×3L=3GL,
因4GL>3GL,所以杠杆不再水平平衡,杠杆左端下降,右端上升。
故选:C。
【点评】本题考查了杠杆平衡条件的应用,杠杆是否平衡取决于力和力臂的乘积是否相等,单独比较力或力臂大小不能得出正确结果。
9.【分析】根据杠杆原来平衡,设移动的距离为L,再比较F1(L1﹣L)和F2(L2﹣L)即可作出判断。
【解答】解:
原来平衡时,由杠杆的平衡条件可得F1?AO=F2?BO,
因为AO>BO,所以F1<F2;
设向支点O移动相同的距离为L,
则A端力与力臂的乘积为:F1(AO﹣L)=F1AO﹣F1L,
B端力与力臂的乘积为:F2(BO﹣L)=F2BO﹣F2L,
因F1<F2,则F1L<F2L,
所以F1(AO﹣L)>F2(BO﹣L),
则杠杆的A端向下倾斜;
故选:B。
【点评】用杠杆的平衡条件,判断出力与力臂乘积的变化值,从而判断出某些量的大小,也是杠杆知识的一种基本应用。
10.【分析】利用下列知识分析判断:
(1)支点:硬棒绕着转动的点叫支点;
(2)支点到力的作用线的距离叫力臂;
(3)对杠杆的分类方法:动力臂大于阻力臂的杠杆为省力杠杆;动力臂小于阻力臂的杠杆为费力杠杆;动力臂等于阻力臂的杠杆为等臂杠杆;
(4)定滑轮的作用,:改变力的方向,但不能省力。
【解答】解:
A、滑轮组C的轴固定不动,为定滑轮,定滑轮的作用是改变力的方向,而不能省力,故A错;
B、由图可知吊桥绕着B点转动,所以护城河上安装的吊桥的支点是B点,故B错;
CD、如图,支点B到力的作用线的距离BD为动力臂L1,
在匀速拉起吊桥时,拉力的作用点是A点,阻力的作用点是桥AB的中点,过支点B做阻力作用线的垂线得到的线段,即为阻力臂L2,比较两力臂的大小可知,它的动力臂大于阻力臂,所以属于一个省力杠杆;故C错、D正确。
故选:D。
【点评】解题本题要求学生知道支点及力臂的定义、定滑轮的作用,在解题时先找出支点的位置,然后根据力臂的定义判断动力臂与阻力臂的长短。
11.【分析】(1)杠杆分类:动力臂小于阻力臂的杠杆是费力杠杆;动力臂大于阻力臂的杠杆是省力杠杆;动力臂等于阻力臂的杠杆是等臂杠杆;
(2)根据内外气压的大小分析
【解答】解:
AB、用力压下手柄过程中,手柄的动力臂大于阻力臂,为省力杠杆,故AB错误;
CD、灭火器在使用的过程中,里面的气压大于外界的气压,干粉在压强差的作用下被喷出,故C错误、D正确。
故选:D。
【点评】本题利用考查了学生对杠杆分类方法、大气压强的了解与掌握,利用所学知识解释了有关灭火器的几个问题,体现了学以致用,有意义!
12.【分析】杠杆的五个要素:支点:杠杆绕着转动的点。
动力:使杠杆转动的力。动力臂:从支点到动力作用线的距离。
阻力:阻碍杠杆转动的力。阻力臂:从支点到阻力作用线的距离。
杠杆的平衡条件:动力×动力臂=阻力×阻力臂。
【解答】解:ABC、由图可见,杠杆绕O点转动,O为支点;作用在M点向下的是动力,是手对筷子的力FM,故B错误;作用在N点向上的力是阻力FN,故C正确;分别从支点O向阻力作用线作垂线,就得到阻力臂0N,用LN表示,动力臂是OM,故A错误;如下图:
D、把食物靠近支点放置时,阻力臂变小,根据杠杆的平衡条件可知食指对筷子上M点的压力FM变小,故D错误;
故选:C。
【点评】本题考查了力臂的画法和杠杆的平衡条件,画力臂的方法:首先确定支点、动力、阻力。然后用虚线画出动力和阻力的作用线,再做出支点力的作用线的距离,最后标出动力臂和阻力臂。
13.【分析】力臂是指从支点到力的作用线的距离,据此确定拉力F力臂。
【解答】解:
由图可知,O为支点,OB是从支点到拉力F的作用线的距离,所以OB是拉力F的力臂。
故选:A。
【点评】本题考查力臂的画法,记住:力臂是从支点到力的作用线的距离。
二.多选题(共3小题)
14.【分析】杠杆的分类和特点,主要包括以下几种:
①省力杠杆,动力臂大于阻力臂,省力但费距离;
②费力杠杆,动力臂小于阻力臂,费力但省距离;
③等臂杠杆,动力臂等于阻力臂,既不省距离也不省力。
【解答】解:苍蝇拍在使用过程中,阻力臂大于动力臂,故是费力杠杆,但能省距离。
故选:BC。
【点评】本题考查了生活中的物品和物理知识的联系,体现了物理来源于生活,服务于生活的宗旨,平时要养成多观察多思考的习惯,生活中处处有物理,每一件工具和物品都蕴含着丰富的物理知识。
15.【分析】结合图片和生活经验,判断杠杆在使用过程中,动力臂和阻力臂的大小关系,再判断它是属于哪种类型的杠杆。
【解答】解:①核桃夹在使用过程中,动力臂大于阻力臂,是省力杠杆;
②船桨在使用过程中,动力臂小于阻力臂,是费力杠杆;
③手推车在使用过程中,动力臂大于阻力臂,是省力杠杆;
④碗夹在使用过程中,动力臂小于阻力臂,是费力杠杆;
属于费力杠杆的是②④。
故选:BD。
【点评】本题考查的是杠杆的分类,主要包括以下几种:①省力杠杆,动力臂大于阻力臂;②费力杠杆,动力臂小于阻力臂;③等臂杠杆,动力臂等于阻力臂。
16.【分析】(1)杠杆的分类:①省力杠杆,动力臂大于阻力臂;②费力杠杆,动力臂小于阻力臂;③等臂杠杆,动力臂等于阻力臂。
(2)要使杠杆平衡,作用在杠杆上的两个力(用力点、支点和阻力点)的大小跟它们的力臂成反比。
【解答】解:(1)由图可见,桔槔是不等臂杠杆,动力臂大于阻力臂,是省力杠杆,故AC不正确,符合题意;
(2)向井内放送水桶时,人用的力通过杠杆原理,与石头的重力相关,一般比木桶的重力要大,故B说法不正确,符合题意;
(3)往上提水时,因为有石头帮忙,人的力气比水和桶的总重力小,故D选项说法正确,不符合题意。
故选:ABC。
【点评】本题考查了杠杆的应用,属于基础知识的考查,注重了物理知识和生活实际的联系。
三.填空题(共10小题)
17.【分析】(1)力的三要素有:力的大小、方向、作用点,它们都影响力的作用效果。
(2)结合图片和生活经验,先判断杠杆在使用过程中,动力臂和阻力臂的大小关系,再判断它是属于哪种类型的杠杆。
【解答】解:
(1)由图可看出,力的大小和方向相同,作用点A、B不同,在B点比A点更易夹碎核桃,说明力的作用效果与作用点有关。
(2)在使用核桃夹时,动力臂大于阻力臂,是省力杠杆。
故答案为:作用点;省力。
【点评】本题考查了力的作用效果、杠杆的分类,属于基础题目。
18.【分析】知道“给我一根杠杆和支点,我就能撬动地球”是古希腊学者阿基米德的一句豪言壮语。
【解答】解:
“给我一个支点,我就能撬动地球”是古希腊学者阿基米德的一句豪言壮语;阿基米德总结出的杠杆平衡条件,也被称为杠杆原理;
故答案为:阿基米德;杠杆。
【点评】本题考查了物理规律及其对应的科学家,考查的是物理学史,属于基础知识,平时在学习过程中应加强记忆。
19.【分析】结合图片,先确定支点,再根据动力臂和阻力臂的大小关系判断它是属于哪种类型的杠杆。
由杠杆的平衡条件可知,在阻力和阻力臂不变的情况下,动力臂越长越省力。
【解答】解:
由图知,撬棒在使用过程中,绕B点转动,则B点为支点,并且动力臂大于阻力臂,是省力杠杆。
由杠杆的平衡条件可知,在阻力和阻力臂不变的情况下,动力臂越长越省力;所以,在用力方向不变的情况下该人想用更小的力撬起石头,那么他的手应该向远离支点O方向移动,这样动力臂变长了,就越省力。
故答案为:B;省力;远离。
【点评】此题考查的是杠杆的分类和特点,主要包括以下几种:①省力杠杆,动力臂大于阻力臂,省力但费距离;②费力杠杆,动力臂小于阻力臂,费力但省距离;③等臂杠杆,动力臂等于阻力臂,既不省距离也不省力。
同时还考查了学生用杠杆的平衡条件分析问题的能力。
20.【分析】力臂是从支点到力的作用线的距离,由支点向力的作用线做垂线,垂线段的长度即为力臂。根据杠杆的平衡条件分析力F的变化。
【解答】解:
由图可知,AB是力F的作用线,OA⊥AB,OA为支点到力F的作用线的距离,所以线段OA表示力F的力臂。
如果拉力一直保持水平方向拉至杠杆到竖直方向,在拉动过程中,重力的力臂减小,如图:
;
根据杠杆平衡条件可知,拉力F的大小将变小。
故答案为:OA;变小。
【点评】本题考查了杠杆的相关知识,考生需要根据力臂的定义在图中识别出已知力F的力臂。引导教学要注重基本概念的理解和落实。
21.【分析】结合生活经验,要判断杠杆的类型,可依据杠杆的动力臂和阻力臂大小关系:若动力臂大于阻力臂,则是省力杠杆;若动力臂小于阻力臂,则是费力杠杆;若动力臂等于阻力臂,则为等臂杠杆。
【解答】解:
我们在使用①切纸刀、②钢丝钳时,都是动力臂大于阻力臂,都是为了省力,所以它们都是省力杠杆;
我们在使用③镊子、⑤食品钳时,都是动力臂小于阻力臂,所以它们都是费力杠杆;
④从摩天轮自身处于平衡时来分析,左右两侧物体的重力分别为动力和阻力,支点在圆心处,可以构成一个等臂杠杆。
故答案为:①②;③⑤;④。
【点评】该题考查了学生对物理模型的抽象、分析能力。判断杠杆的类型可结合生活经验和动力臂与阻力臂的大小关系来判断。注意天平是典型的等臂杠杆。
22.【分析】(1)抬起木材一端时,以另一端为支点;利用杠杆平衡条件:动力×动力臂=阻力×阻力臂可解答此题;
(2)求出将它竖直起来时木材的重心离水平面的高度,即为重心上升的高度,最后根据W=Gh求出需要做的功。
【解答】解:
(1)已知木材质量为1.2kg,则其重力G=mg=1.2kg×10N/kg=12N,
设其长度为L;抬起一端时,以另一端为支点,其重心到支点的距离为L,动力臂为L,
根据杠杆平衡条件则有:F×L=G×L;
解得F=G=×12N=6N,即至少要用6N的力;
(2)将它竖直起来时,木材的重心离水平面的高度为h===0.4m,
则至少需要做的功:W=Gh=12N×0.4m=4.8J。
故答案为:6;4.8。
【点评】知道杠杆平衡的条件,会熟练应用杠杆平衡的条件计算相关的力和力臂以及功的计算公式的掌握和应用,明确克服重力做功就是所需要做的功,求重心上升的高度是本题的易错点,要求学生要认真分析。
23.【分析】该题考查了学生对物理模型的抽象、分析能力。判断杠杆的类型可结合生活经验和动力臂与阻力臂的大小关系来判断。常见的等臂杠杆有天平、跷跷板、定滑轮。
【解答】解:我们使用①剪铁皮的剪刀、⑥羊角锤、⑦老虎钳都是为了省力,并且在使用的过程中都是动力臂大于阻力臂,所以它们都是省力杠杆;
我们使用③筷子、⑤镊子、⑧钓鱼竿都是为了省距离,并且在使用的过程中都是动力臂小于阻力臂,所以它们都是费力杠杆;
天平是典型的等臂杠杆,它的动力臂等于阻力臂;
在使用定滑轮时既不省力也不省距离,它实质上是一个等臂杠杆。
故答案为:①⑥⑦;③⑤⑧;②④。
【点评】本题考查了杠杆、滑轮的分类和使用特点。省力杠杆省力但费距离,费力杠杆费力但省距离,等臂杠杆不省力也不省距离。既省力又省距离的机械是不存在的。
24.【分析】结合图片和生活经验,先判断船桨在使用过程中,动力臂和阻力臂的大小关系,再判断它是属于哪种类型的杠杆,进而确定是省距离还是费距离。
【解答】解:
因为船桨在使用过程中,动力臂小于阻力臂,所以船桨属于费力杠杆,但省距离,这样运动员的手移动很小的距离时,可使船桨在水中划过的距离很大,从而加快了赛艇前进的速度。
故答案为:费力;大于。
【点评】本题考查了杠杆的分类和特点,属于基本内容,比较简单。
25.【分析】根据杠杆原理进行分析,在力一定的情况下,分析力臂的大小关系,力臂的越大越容易被大风吹倒。
【解答】解:我们可以把树看作一个杠杆模型,支点为树根处,当都受到同样大小的风力作用时,树越高,其力臂越大,越容易被风吹倒。
故答案为:杠杆;乙。
【点评】本题考查杠杆平衡条件的应用,力与力臂的乘积越大,其作用效果越大。
26.【分析】气球膨胀后气球和篮球的总体积增大,根据阿基米德原理判断它们所受浮力的变化;再根据F拉=G总﹣F浮判断杠杆左端产生拉力的变化,最后根据杠杆的平衡条件判断杠杆的平衡情况。
【解答】解:因为杠杆原来是平衡的,
所以:G总×l1=G码×l2;
气球膨胀后,气球和篮球的总体积增大,
根据公式F浮=ρ气gV排得到,它们受到的浮力F浮增大;
根据F拉=G总﹣F浮可知,总重力G总不变,气球和篮球对杠杆的拉F拉变小;
因为杠杆的动力臂l1、阻力臂l2和阻力G码(钩码重力)保持不变,
根据杠杆的平衡条件得到:F拉×l1<G码×l2;
那么杠杆的左端向上翘起,这是因为浮力增大的缘故。
故答案为:左;浮力增大。
【点评】知道影响浮力大小的因素,能够正确的进行受力分析是解决本题的关键。
四.作图题(共7小题)
27.【分析】(1)根据重力的方向是竖直向下的,过重心做竖直向下的力即可。
(2)杠杆平衡条件:动力×动力臂=阻力×阻力臂(F1L1=F2L2),在阻力跟阻力臂的乘积一定时,动力臂越长,动力越小。
【解答】解:重力的方向是竖直向下的,过物体重心画一条带箭头的竖直向下的有向线段,用G表示;
由杠杆平衡条件F1L1=F2L2可知,在阻力跟阻力臂的乘积一定时,动力臂越长,动力越小;图中支点在O点,左端距离支点最远,因此OA作为动力臂时最长,此时动力最小,由图知动力的方向应该垂直于OA向上,如下图所示:
【点评】本题主要考查了重力示意图的画法和杠杆中最小力的问题。解决此类题目的关键是确定出最长的力臂,并根据力臂的画法做出最小的力。
28.【分析】力臂是支点到力的作用线的距离,作图时把握住力和力臂的垂直关系即可做出动力。
【解答】解:过力臂L1的末端,作垂直于L1的直线,与杠杆的交点为力F1的作用点,为使杠杆平衡,力F1的方向应向上,据此画出力F1的示意图,如图所示:
【点评】本题考查了力臂的画法。知道力臂是从支点到力的作用线的垂直距离是关键,易错点将垂足当做动力作用点。
29.【分析】力臂的画法:首先确定支点O;然后延长动力的作用线(用虚线);再由支点向动力作用线做垂线(用虚线);用双箭头标出L1.先确定阻力作用点(即B点),然后过阻力作用点表示阻力的方向(即竖直向小);
【解答】解:从支点O作动力F作用线的垂线段,垂线段的长度即为动力臂L1;
阻力作用点在点B,方向竖直向下,如图所示:
【点评】明确力臂的概念,从支点向力的作用线画垂线,即可找出力臂的位置,阻力是阻碍杠杆转动的力,明确了这些基本概念便不难解决。
30.【分析】已知支点,画出动力作用线,过支点作垂直于力的作用线的垂线段,可得力臂。
【解答】解:
过支点O作垂直于动力作用线的垂线段,可得动力臂L1,如图所示;
【点评】本题考查了力臂的画法,属于基础题目。
31.【分析】支点到作用线的距离为力臂;过动力臂的末端作一条垂直于力臂的直线,可得动力作用线,进而画出动力F1。
【解答】解:
过力臂L1的末端作一条垂直于力臂的直线即为动力F1的作用线,与杠杆的交点A为动力作用点,为使杠杆平衡,动力的方向应斜向下,据此作出F1的示意图;
过支点O作垂直于阻力F2作用线的垂线段,即为阻力臂L2,如图所示:
【点评】知道杠杆中力与力臂的关系,会根据力臂的画法作出杠杆的作用力或力臂。
32.【分析】先画出力F1的作用线,然后过支点作F1作用线的垂线段,可得其力臂。
【解答】解:
反向延长F1画出F1的作用线,过支点O作F1作用线的垂线段,即为F1的力臂L1,如图所示:
【点评】本题考查了力臂的画法。画力臂时关键是要画出支点到力的作用线的垂线段。
33.【分析】已知动力和阻力,根据力臂的画法,先确定支点O,再过支点作动力作用线和阻力作用线的垂线段,即可画出动力臂和阻力臂。
【解答】解:已知支点为O,延长F2画出力的作用线,过支点O作力F2作用线的垂线段L2,过支点O作力F1作用线的垂线段L1,则L1、L2即为所求作的力臂。如图所示:
【点评】力臂的画法:①首先根据杠杆的示意图,确定杠杆的支点。②确定力的作用点和力的方向,画出力的作用线。③从支点向力的作用线作垂线,支点到垂足的距离就是力臂。
五.实验探究题(共2小题)
34.【分析】(1)杠杆倾斜时,杠杆的重心偏向杠杆下沉的一端,左、右两端的螺母(或一端的螺母)要向杠杆上翘的一端调节;实验前先要调节杠杆在水平位置平衡,这是为使杠杆所受的重力通过支点,从而可以不考虑杠杆的重力对其转动的影响;
(2)若采用弹簧测力计,拉力的方向由竖直向下逐渐向右倾斜时,判断出动力臂的变化,根据杠杆平衡原理即可判断动力大小;
(3)杠杆的重心过支点,可以消除杠杆重对杠杆平衡的影响。
(4)杠杆在水平位置平衡时,力的方向与杠杆垂直,力臂的长度可以直接从杠杆上读出来。
【解答】解:(1)将杠杆中点置于支架上,当杠杆静止时,发现杠杆右端下沉,左端上翘,平衡螺母向上翘的左端移动,即把杠杆左端的平衡螺母向左调节,直到杠杆在不挂钩码时,保持水平位置静止状态;
(2)杠杆平衡后,若在A点挂4个钩码,则左边点重力为4G,
又因为力臂OA=3,左边力臂OB=2,
实验由杠杆的平衡条件(F1l1=F2l2)可知:4G×3=F1×2,实验F1=6G;故应在B点应挂6个钩码,才能使杠杆恢复平衡;
若采用弹簧测力计,拉力的方向由竖直向下逐渐向右倾斜时,动力臂变小了,根据杠杆平衡条件可知:弹簧测力计的示数将变大了。
(3)如图乙示装置进行探究,杠杆的重心没有通过支点,杠杆的重对杠杆平衡有影响
(4)杠杆处于静止状态或匀速转动状态都叫杠杆平衡,所以小海的说法是对的;
力臂等于支点到力的作用线的距离,在小红的实验方案中,当杠杆在水平位置平衡时,力的方向与杠杆垂直,力臂可以从杠杆标尺刻度上直接读出来。而甲实验方案中的力臂不便于测量,所以,小红的实验方案好。
故答案为:
(1)左;水平;
(2)6;变大;动力臂变小了;
(3)杠杆自身的重力;
(4)对;小红; 便于测量力臂。
【点评】探究杠杆平衡条件时,使杠杆在水平位置平衡,便于测量力臂大小,杠杆的重心通过支点,消除杠杆重对杠杆平衡的影响,使实验简单化,便于探究。
35.【分析】(1)在调平杠杆平衡时,杠杆的哪端高,平衡螺母要向哪端移动;
(2)①根据杠杆的平衡条件计算出在B点挂的钩码个数或拉力的大小;使杠杆平衡在水平位置的目的是便于测量力臂;
②当拉力F向右倾斜时,分析出力臂的变化结合杠杆的平衡条件判断力的变化;
(3)根据杠杆的平衡条件分析即可。
【解答】解:(1)杠杆静止时,杠杆左端下沉,说明右端偏高,平衡螺母需向右调节;
(2)①设杠杆每个格的长度为L,每个钩码的重力为G,根据杠杆的平衡条件:
FALA=FBLB,即2G×3L=FB×2L,解得FB=3G,需挂3个钩码。
使杠杆平衡在水平位置的目的是便于测量力臂;
②若拉力F向右倾斜时,此时F的力臂变短,根据杠杆的平衡条件,力变大;
(3)若不计杠杆的重力,根据杠杆的平衡条件:
F向上L向上=F向下L向下
F′?4L=3G?8L
解得F′=6G=6×0.5N=3N,
实验中发现弹簧测力计的示数为3.5N,数据不符合杠杆平衡条件,原因是杠杆自身有重力。
故答案为:(1)右;(2)①3;便于测量力臂;②变大;F的力臂变短;(3)杠杆自身有重力。
【点评】此题是探究杠杆平衡实验,考查了杠杆的调平及杠杆平衡条件的应用,在利用平衡条件公式时,要注意分析力和对应的力臂。
六.计算题(共3小题)
36.【分析】确定独轮车的支点,然后找出动力臂和阻力臂,动力和阻力,根据杠杆的平衡条件进行计算。
【解答】解:(1)独轮车的车辆轮轴处是支点,其中重力G是阻力,支点到重力作用线的距离是阻力臂,故阻力臂是0.4m;
力F1是动力,支点到力F作用线的距离是动力臂,故动力臂是0.4m+1.2m=1.6m;
(2)由杠杆的平衡条件可知:F1×L动=G×L阻,得F1===250N。
答:(1)F1的力臂l1的大小是1.6m;
(2)F1的大小是250N。
【点评】此题考查了杠杆平衡条件的应用,要掌握杠杆的平衡条件,确定杠杆受到的力及对应的力臂,根据杠杆的平衡条件进行求解。
37.【分析】图中O为支点,OA为重力的力臂,OB为拉力的力臂,根据杠杆平衡条件可求出在B点挂的物体的重力大小,然后即可求出质量。
【解答】解:
由题可知,F1=196N,拉力的力臂OA=OB+AB=0.3cm+0.9cm=1.2m,重力的力臂OB=30cm=0.3m;
根据杠杆平衡条件可得:F1×OA=G×OB,
则G===7845N,
所以质量m===80kg。
答:B点能挂的物体质量最大为80kg。
【点评】本题考查了杠杆平衡条件的应用,关键是要找准力臂,计算时要注意力与力臂的对应。
38.【分析】杠杆水平平衡,先求出动力臂、阻力臂、阻力,再利用杠杆平衡条件求细绳的拉力。
【解答】解:
如下图所示,由于杠杆水平平衡,在Rt△OBA中,∠OAB=30°,则OB=×OA=×10cm=5cm,即动力臂为OB等于5cm,阻力臂为OC等于10cm,
杠杆受到的阻力F阻=G球=m球g=5kg×10N/kg=50N,
由杠杆平衡条件可得:F×OB=F阻×OC,
即:F×5cm=50N×10cm,
解得:F=100N。
答:细绳的拉力为100N。
【点评】本题考查了重力公式和杠杆平衡条件的应用,利用直角三角形的角边关系求出动力臂大小是关键。
七.解答题(共2小题)
39.【分析】如图,假设支点为O,知道杠杆两端受力的大小,找出两边力的力臂,根据杠杆平衡条件求解;若杠杆两端所挂重物各增加50N,假设支点为O′,知道杠杆两端受力的大小,找出两边力的力臂,根据杠杆平衡条件求解。
【解答】解:
如图,O为支点,
F1=200N,F2=50N,
因为杠杆平衡,
所以F1LOB=F2(Lm﹣LOB),
即:200N×LOB=50N×(1m﹣LOB),
所以LOB=0.2m。
同理,若杠杆两端所挂重物各增加50N,假设支点为O′,
F2′=50N+50N=100N;F1′=200N+50N=250N,
F1′LOB′=F2′(Lm﹣LOB′),
250N×LOB′=100N×(1m﹣LOB′),
解得LOB′=0.285m。
答:(1)支点应距B物体那端0.2米时,杠杆才能平衡;(2)若杠杆两端所挂重物各增加50N,支点应距左端0.285m才能使杠杆平衡。
【点评】本题考查了学生对杠杆平衡条件的掌握和运用,因为支点待确定,有难度,最好画出杠杆示意图帮助理清思路。
40.【分析】(1)根据题意对扁担进行受力分析;
(2)以扁担的左端点为支点,确定动力臂和阻力臂的大小,由杠杆平衡条件求出乙对扁担的力,
根据力的作用是相互的求出扁担对乙的压力;
(3)以扁担的右端点为支点,确定动力臂和阻力臂的大小,由杠杆平衡条件求出甲对扁担的力,
根据力的作用是相互的求出扁担对甲的压力。
【解答】解:扁担受力如图所示;
以扁担的左端点为支点,由杠杆平衡条件:动力×动力臂=阻力×阻力臂,
答:两人肩上各担200N,120N的力。
【点评】本题考查了力的平衡条件与杠杆平衡条件的应用,根据题意作出图示,使物理情景直观、明了,有助于解题。
声明:试题
同课章节目录
- 第一章 打开物理世界的大门
- 第一节 走进神奇
- 第二节 探索之路
- 第三节 站在巨人的肩膀上
- 第二章 运动的世界
- 第一节 动与静
- 第二节 长度与时间的测量
- 第三节 快与慢
- 第四节 科学探究:速度的变化
- 第三章 声的世界
- 第一节 科学探究:声音的产生与传播
- 第二节 声音的特性
- 第三节 超声与次声
- 第四章 多彩的光
- 第一节 光的反射
- 第二节 平面镜成像
- 第三节 光的折射
- 第四节 光的色散
- 第五节 科学探究:凸透镜成像
- 第六节 神奇的眼睛
- 第五章 质量与密度
- 第一节 质量
- 第二节 学习使用天平和量筒
- 第三节 科学探究:物质的密度
- 第四节 密度知识的应用
- 第六章 熟悉而陌生的力
- 第一节 力
- 第二节 怎样描述力
- 第三节 弹力与弹簧测力计
- 第四节 来自地球的力
- 第五节 科学探究:摩擦力
- 第七章 力与运动
- 第一节 科学探究:牛顿第一定律
- 第二节 力的合成
- 第三节 力的平衡
- 第八章 压强
- 第一节 压力的作用效果
- 第二节 科学探究:液体的压强
- 第三节 空气的“力量”
- 第四节 流体压强与流速的关系
- 第九章 浮力
- 第一节 认识浮力
- 第二节 阿基米德原理
- 第三节 物体的浮与沉
- 第十章 机械与人
- 第一节 科学探究:杠杆的平衡条件
- 第二节 滑轮及其应用
- 第三节 做功了吗
- 第四节 做功的快慢
- 第五节 机械效率
- 第六节 合理利用机械能
- 第十一章 小粒子与大宇宙
- 第一节 走进微观
- 第二节 看不见的运动
- 第三节 探索宇宙
