六年级下册数学课件-2.7 圆锥的体积(1) 西师大版(2014秋)(共20张PPT)
文档属性
| 名称 | 六年级下册数学课件-2.7 圆锥的体积(1) 西师大版(2014秋)(共20张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 西师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-01-09 08:10:56 | ||
图片预览






文档简介
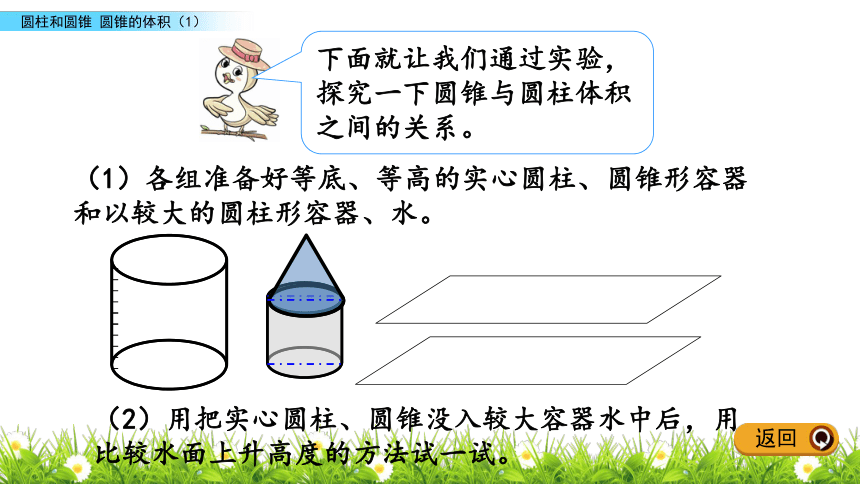
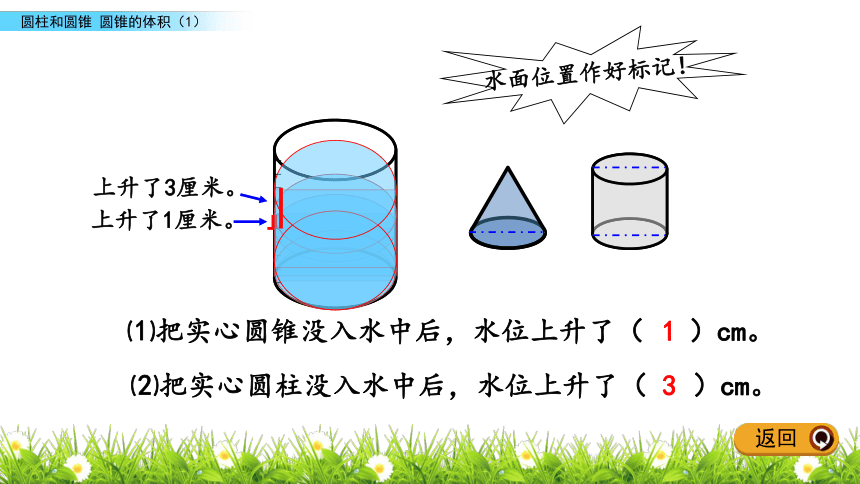
课件20张PPT。圆锥的体积(1)情境导入探究新知课堂小结课后作业圆柱和圆锥课堂练习2我们已经学会计算圆柱的体积,请你回忆一下如何计算圆柱的体积? 情境导入返回1.怎样计算圆柱的体积?V=Sh2.一个圆柱的底面积是60平方分米,高是15分米,它的体积是多少立方分米?V=Sh =60×15 =900(立方分米)返回它占了多大的空间呢?返回圆锥的体积与圆柱的体积有没有关系呢?你能猜测一下等底、等高的圆柱和圆锥的体积之间的关系吗?圆柱的底面是圆,圆锥的底面也是圆。如何计算圆锥的体积呢?探究新知返回怎样计算圆锥的体积呢?例 1返回下面就让我们通过实验,探究一下圆锥与圆柱体积之间的关系。(1)各组准备好等底、等高的实心圆柱、圆锥形容器和以较大的圆柱形容器、水。(2)用把实心圆柱、圆锥没入较大容器水中后,用比较水面上升高度的方法试一试。返回上升了1厘米。上升了3厘米。⑴把实心圆锥没入水中后,水位上升了( )cm。⑵把实心圆柱没入水中后,水位上升了( )cm。水面位置作好标记!13返回通过实验,你发现了什么?圆锥的体积是与它等底等高圆柱体积的三分之一。返回圆锥的体积=圆柱的体积= 底面积 × 高底面积高××V= Sh求出与这个圆锥等底等高的圆柱的体积,圆锥的体积怎样计算?再乘以三分之一,就得到圆锥的体积。返回答:这个零件的体积是100.48立方厘米。一个铅锤高6cm,底面半径4cm。这个铅锤的体积是多少立方厘米? 先求铅锤的底面积用3.14×42。×3.14×42×6=3.14×42×2=100.48(厘米)例 3返回(1)各组准备好等底、等高的圆柱、圆锥形容器。(2)用倒沙子或水的方法试一试。下面就让我们通过实验,探究一下圆锥与圆柱体积之间的关系。从上面的实验中,你发现了什么?返回
(3)通过实验,你发现圆锥的体积与同它等底、等高的
圆柱的体积之间的关系了吗?三次正好装满。我把圆柱装满水,再往圆锥里倒。正好倒了三次。返回1.填空。
⑴圆锥的体积=( ),用字母表示是( )。
⑵圆柱体积的 与和它( )的圆锥的体积相等。
等底等高×底面积×高V= sh课堂练习返回2.?判断。
⑴ 圆锥的体积等于圆柱体积的3倍。 ( )
⑵ 圆锥的体积等于和它等底等高的圆柱体积的三分之一。 ( )
⑶ 一个圆锥的底面半径扩大3倍,高不变,它的体积也扩大3倍。 ( ) ×√×返回3.选择题。
⑴ 把一个圆柱削成最大的圆锥,已知削掉部分是60厘米,这个圆柱的体积是( )立方厘米。
A.20 B.30 C.90 D.180
⑵ 一个圆柱体积可以熔铸成( )个与它等底等高的圆锥体零件。
A.4 B.3 C.2 D.1 CB返回 4.解决问题。(1)一个圆柱的体积是75.36m3,与它等底等高的圆锥的体积
是( )m3。25.12(2)一个圆锥的体积是141.3m3,与它等底等高的圆柱的体积是( )m3。423.9141.3×3=423.9(m3)75.36× =25.12(m3)返回5. 一个圆锥形的零件,底面积是19cm2,高是12cm,这个零件的体积是多少?答:这个零件的体积是76cm3 。×19 ×12=19×4 =76(cm3) 返回★圆锥的体积= ×底面积×高V= Sh课堂小结这节课你们都学会了哪些知识?返回课后作业课本:
第34页第2、3、4题返回
(3)通过实验,你发现圆锥的体积与同它等底、等高的
圆柱的体积之间的关系了吗?三次正好装满。我把圆柱装满水,再往圆锥里倒。正好倒了三次。返回1.填空。
⑴圆锥的体积=( ),用字母表示是( )。
⑵圆柱体积的 与和它( )的圆锥的体积相等。
等底等高×底面积×高V= sh课堂练习返回2.?判断。
⑴ 圆锥的体积等于圆柱体积的3倍。 ( )
⑵ 圆锥的体积等于和它等底等高的圆柱体积的三分之一。 ( )
⑶ 一个圆锥的底面半径扩大3倍,高不变,它的体积也扩大3倍。 ( ) ×√×返回3.选择题。
⑴ 把一个圆柱削成最大的圆锥,已知削掉部分是60厘米,这个圆柱的体积是( )立方厘米。
A.20 B.30 C.90 D.180
⑵ 一个圆柱体积可以熔铸成( )个与它等底等高的圆锥体零件。
A.4 B.3 C.2 D.1 CB返回 4.解决问题。(1)一个圆柱的体积是75.36m3,与它等底等高的圆锥的体积
是( )m3。25.12(2)一个圆锥的体积是141.3m3,与它等底等高的圆柱的体积是( )m3。423.9141.3×3=423.9(m3)75.36× =25.12(m3)返回5. 一个圆锥形的零件,底面积是19cm2,高是12cm,这个零件的体积是多少?答:这个零件的体积是76cm3 。×19 ×12=19×4 =76(cm3) 返回★圆锥的体积= ×底面积×高V= Sh课堂小结这节课你们都学会了哪些知识?返回课后作业课本:
第34页第2、3、4题返回
