2018-2019学年江苏省常州市14校联盟高一(上)期中数学试卷(解析版)
文档属性
| 名称 | 2018-2019学年江苏省常州市14校联盟高一(上)期中数学试卷(解析版) |  | |
| 格式 | zip | ||
| 文件大小 | 74.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-01-10 22:27:36 | ||
图片预览




文档简介
2018-2019学年江苏省常州市14校联盟高一(上)期中数学试卷
一、填空题(本大题共14小题,共56.0分)
设集合A={x|x>0},B={x|-1<x<3},则A∩B=______.
函数f(x)=ax-2+3(a>0,且a≠1)的图象所经过的定点坐标为______.
给出下列三个函数:①y=
??
2
?2??
???2
;②y=
??
3
+??
??
2
+1
;③y=
??
2
. 其中与函数f(x)=x相同的函数的序号是______.
满足{1,2}?A?{1,2,3,4}的集合A的个数是______.
已知f(
??
-2)=x,则f(-1)=______.
已知函数y=f(x)是R上的偶函数,且x≥0时,f(x)=x2+x,则当x<0时,函数f(x)的解析式为f(x)=______.
直线y=3与函数y=2x,y=3?2x图象的两个交点间距离为______.
已知函数f(x)=
??
2
?2??,??≥0
?2??,??<0
,若f(4)>f(t),则实数t的取值范围为______.
已知集合A={x|x2-3x-4=0},B={x|mx+1=0},且B?A,则实数m的值为______.
记函数f(x)=
3???
+
???1
的定义域为集合M,函数g(x)=4x-1,x∈(-∞,1)的值域为集合N,则M∪N=______.
当x∈[-1,2]时,函数f(x)=
1
3??+??
恒有意义,则实数t的取值范围为______.
已知f(x)为定义在R上的偶函数,且在(0,+∞)上为单调增函数,f(1)=0,则不等式
??(??)+??(???)
??
>0的解集为______.
若函数y=f(x+1)+3是定义在R上的奇函数,则f(e)+f(2-e)=______.
已知函数f(x)=
2
??
2
,??>1
?
??
2
+2????,??≤1
,若存在a,b∈R,且a≠b,使得f(a)=f(b)成立,则实数k的取值范围是______.
二、解答题(本大题共6小题,共64.0分)
已知集合A={y|y=3x-1,0≤x≤1},B={x|(x-a)[(x-(a+3))]<0}. (1)若a=1,求A∪B; (2)若A∩B=?,求实数a的取值范围.
计算: (1)(
1
300
)
?
1
2
+
81
3
4
+(
2
3
)
0
-10×(2?
3
)
?1
; (2)
??
????4
+????
??
5
25+lg25+lg2?lg50+(lg2)2
已知函数f(x)=1-
??
3
??
+1
是奇函数. (1)求实数m的值; (2)用定义证明f(x)是R上的增函数;并求当x∈[-2,2]时函数f(x)的值域.
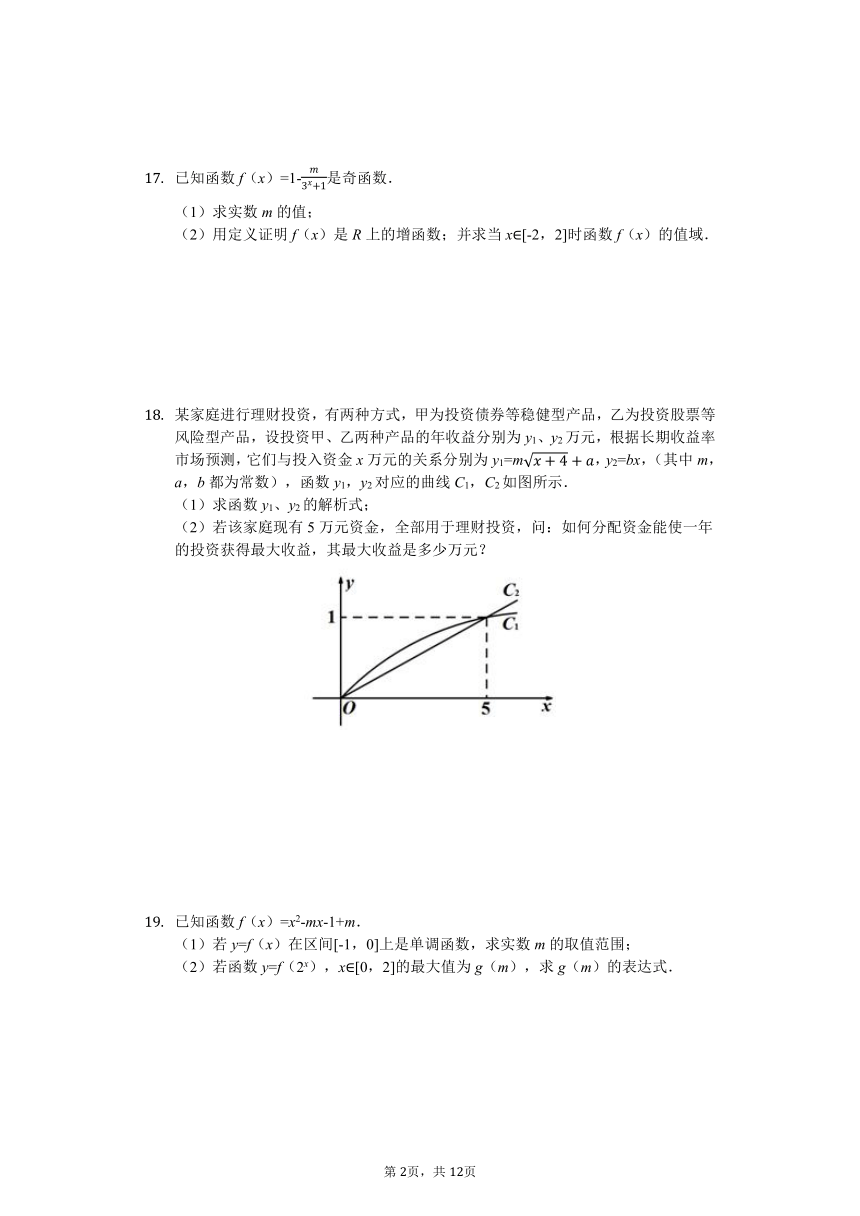
某家庭进行理财投资,有两种方式,甲为投资债券等稳健型产品,乙为投资股票等风险型产品,设投资甲、乙两种产品的年收益分别为y1、y2万元,根据长期收益率市场预测,它们与投入资金x万元的关系分别为y1=m
??+4
+??,y2=bx,(其中m,a,b都为常数),函数y1,y2对应的曲线C1,C2如图所示. (1)求函数y1、y2的解析式; (2)若该家庭现有5万元资金,全部用于理财投资,问:如何分配资金能使一年的投资获得最大收益,其最大收益是多少万元?
已知函数f(x)=x2-mx-1+m. (1)若y=f(x)在区间[-1,0]上是单调函数,求实数m的取值范围; (2)若函数y=f(2x),x∈[0,2]的最大值为g(m),求g(m)的表达式.
设a是实数,函数f(x)=32x+|3x-a|(x∈R). (1)求证:函数f(x)不是奇函数; (2)当a≤0时,解关于x的不等式f(x)>a2; (3)求函数f(x)的值域(用a表示).
答案和解析
1.【答案】(0,3) 【解析】
解:A∩B=(0,3). 故答案为:(0,3). 进行交集的运算即可. 考查描述法的定义,交集的运算.
2.【答案】(2,4) 【解析】
解:当x=2时,f(2)=a2-2+3=a0+3=4,∴函数f(x)=ax-2+3的图象一定经过定点(2,4). 故答案为(2,4). 利用a0=1(a≠0),取x=2,得f(2)=4,即可求函数f(x)的图象所过的定点. 本题考查了含有参数的函数过定点的问题,自变量的取值使函数值不含参数即可求出其定点.
3.【答案】② 【解析】
解:f(x)=x的定义域为R; ①的定义域为{x|x≠2},定义域不同,与f(x)=x不相同; ②的定义域为R,与f(x)=x相同; ③,解析式不同,与f(x)=x不相同. 故答案为:②. 通过求定义域,化简函数,即可找出与f(x)=x相同的函数. 考查函数的定义,判断函数是否相同的方法:定义域和解析式是否都相同.
4.【答案】3 【解析】
解:根据条件知,1,2是A的元素,而3,4中最多有1个为A的元素,所以这样的A为: {1,2},{1,2,3},{1,2,4}; ∴满足条件的集合A有3个. 故答案为:3. 根据子集及真子集的定义即可知1,2∈A,3,4中最多一个属于A,这样即可写出满足条件的集合A,从而得出答案. 考查列举法表示集合,子集及真子集的定义,清楚二者的区别.
5.【答案】1 【解析】
解:根据题意,f(-2)=x, 令-2=-1,则x=1, 则有f(-1)=-1, 故答案为:1. 根据题意,f(-2)=x中令-2=-1,求出x的值,代入f(-2)=x中计算可得答案. 本题考查函数值的计算,关键是特殊值法分析,属于基础题.
6.【答案】x2-x 【解析】
解:根据题意,设x<0,则-x>0, f(-x)=(-x)2+(-x)=x2-x, 又由函数为偶函数,则f(x)=f(-x)=x2-x, 故答案为:x2-x. 根据题意,设x<0,则-x>0,由函数的解析式可得f(-x)=(-x)2+(-x)=x2-x,进而结合函数的奇偶性分析可得答案. 本题考查函数奇偶性的应用,涉及函数解析式的计算,属于基础题.
7.【答案】log23 【解析】
解:联立,可得x=log23; 联立,可得x=0. ∴直线y=3与函数y=2x,y=3?2x图象的两个交点间距离为log23-0=log23. 故答案为:log23. 联立方程组分别求出交点坐标,再由沙尔定理求解. 本题考查指数方程的解法,考查两点间距离的求法,是基础题.
8.【答案】(-4,4) 【解析】
解:函数f(x)=, 可得f(4)=16-8=8, 由f(4)>f(t),可得 或, 即为-4<t<0或0≤t<4, 则t的取值范围是(-4,4). 故答案为:(-4,4). 由分段函数可得f(4)=8,讨论x<0,x≥0,解不等式即可得到所求范围. 本题考查分段函数的运用:求函数值和解不等式,考查分类讨论思想方法和运算能力,属于基础题.
9.【答案】-
1
4
或0或1. 【解析】
解:∵集合A={x|x2-3x-4=0}={-1,4}, B={x|mx+1=0},且B?A, ∴当m=0时,B=?,成立; 当m≠0时,B={-}, ∴-=-1或-=4, 解得m=1或m=-. ∴实数m的值为-或0或1. 故答案为:-或0或1. 求出集合A={-1,4},B={x|mx+1=0},且B?A,当m=0时,B=?,成立;当m≠0时,B={-},从而-=-1或-=4,由此能求出实数m的值. 本题考查实数值的求法,考查集合的包含关系等基础知识,考查运算求解能力,是基础题.
10.【答案】(-1,3] 【解析】
解:要使f(x)有意义,则:; ∴1≤x≤3; ∴M=[1,3]; ∵x<1; ∴0<4x<4; ∴-1<4x-1<3; ∴N=(-1,3); ∴M∪N=(-1,3]. 故答案为:(-1,3]. 可分别求f(x)的定义域,g(x)的值域,从而得出集合M,N,然后进行并集的运算即可. 考查函数定义域、值域的定义及求法,指数函数的单调性,以及并集的运算.
11.【答案】(3,+∞) 【解析】
解:要使f(x)=有意义,则; ∵x∈[-1,2]时,f(x)恒有意义; ∴; ∴t>3; ∴实数t的取值范围为(3,+∞). 故答案为:(3,+∞). 可得出f(x)有意义时,,而x∈[-1,2]时,函数f(x)恒有意义,从而得出,这样即可求出t的范围. 考查函数定义域的概念及求法,能用数轴表示集合.
12.【答案】(-1,0)∪(1,+∞) 【解析】
解:根据题意,f(x)在(0,+∞)上为单调增函数,且f(1)=0, 在区间(0,1)上,f(x)<0,在(1,+∞)上,f(x)>0, 又由函数为偶函数,则>0?>0?xf(x)>0?xf(|x|)>0?或; 解可得:x>1或-1<x<0, 即不等式的解集为(-1,0)∪(1,+∞); 故答案为:(-1,0)∪(1,+∞). 根据题意,结合函数在(0,+∞)上的单调性以及特殊值,分析可得在区间(0,1)上,f(x)<0,在(1,+∞)上,f(x)>0;结合函数的奇偶性分析可得>0?xf(|x|)>0?或;解可得x的取值范围,即可得答案. 本题考查函数的奇偶性与单调性的综合应用,注意将原不等式变形,属于综合题.
13.【答案】-6 【解析】
解:根据题意,若函数y=f(x+1)+3是定义在R上的奇函数, 则[f(x+1)+3]+[f(-x+1)+3]=0,变形可得f(x+1)+f(-x+1)=-6, 令x+1=e,则x=e-1, 则有f(e)+f(2-e)=-6; 故答案为:-6. 根据题意,由奇函数的性质可得[f(x+1)+3]+[f(-x+1)+3]=0,变形可得f(x+1)+f(-x+1)=-6,令x+1=e,代入计算可得答案. 本题考查函数奇偶性的应用,涉及函数的对称性,属于基础题.
14.【答案】k<1或k>
3
2
【解析】
解:函数f(x)=, 存在a,b∈R,且a≠b,使得f(a)=f(b)成立, 可得f(x)在R上不单调, 由x>1时,f(x)递增, 由f(x)=2x2,x>1为增函数,且x=1时,2x2=2, 得x≤1时,f(x)先增后减,即k<1; 或x=1处的函数值大于2,即-1+2k>2, 解得k<1或k>, 故答案为:k<1或k>. 依题意,在定义域内,f(x)不是单调函数,结合二次函数的图象和性质及分段函数的单调性,可得结论. 本题考查分段函数的应用:判断单调性,考查分类讨论思想,难度中档.
15.【答案】解:A=[-1,2],B=(a,a+3); (1)a=1时,B=(1,4); ∴A∪B=[-1,4); (2)∵A∩B=?; ∴a≥2,或a+3≤-1; ∴a≥2,或a≤-4; ∴实数a的取值范围为{a|a≤-4,或a≥2}. 【解析】
(1)可先求出A=[-1,2],B=(a,a+3),a=1时,得出集合B,然后进行并集的运算即可; (2)根据A∩B=?即可得出a≥2,或a+3≤-1,从而得出实数a的取值范围. 考查描述法和区间表示集合的定义,并集、交集的运算,空集的概念.
16.【答案】解:(1)原式=
300
+
3
4×
3
4
+1-10×(2+
3
)=10
3
+33+1-20-10
3
=8. (2)原式=4+4+2lg5+lg2(1+lg5)+(lg2)2 =8+1+lg5+lg2 =10. 【解析】
(1)利用指数运算性质即可得出. (2)利用对数运算性质及其lg5+lg2=1即可得出. 本题考查了指数与对数运算性质,考查了推理能力与计算能力,属于基础题.
17.【答案】解:(1)根据题意,f(x)为R奇函数, 则f(0)=1-
??
3
0
+1
=0,解可得m=2; 当m=2时,f(x)=1-
2
3
??
+1
=
3
??
?1
3
??
+1
,为奇函数,符合题意; 故m=2; (2)由(1)的结论,f(x)=1-
2
3
??
+1
, 设x1<x2,则f(x1)-f(x2)=(1-
2
3
??
1
+1
)-(1-
2
3
??
2
+1
)=
2(
3
??
1
?
3
??
2
)
(
3
??
1
+1)(
3
??
2
+1)
, 又由x1<x2,则(
3
??
1
-
3
??
2
)<0,(
3
??
1
+1)>0,(
3
??
2
+1)>0, 则f(x1)-f(x2)<0, 则函数f(x)在R上是增函数; 则f(x)max=f(2)=
4
5
,f(x)min=f(-2)=-
4
5
; 则函数f(x)在[-2,2]上的值域为[-
4
5
,
4
5
]. 【解析】
(1)根据题意,由奇函数的性质可得f(0)=1-=0,解可得m的值,验证可得答案; (2)根据题意,由(1)的结论,f(x)=1-,用作差法证明可得f(x)是R上的增函数,据此分析可得函数f(x)的值域,即可得答案. 本题考查函数的奇偶性与单调性的综合应用,关键是求出m的值.
18.【答案】(1)解:由函数y1的图象过点(0,0),(5,1)得
3??+??=1
2??+??=0
,所以
??=?2
??=1
; 由函数y2的图象过点(0,0),(5,1)得5b=1,所以b=
1
5
; 所以y1=
??+4
-2,y2=
1
5
x; (2)设投资甲产品为x万元,则投资乙产品为(5-x)万元,0≤x≤5, 则总收益y=y1+y2=
??+4
-2+
1
5
(5-x)=
??+4
-
1
5
x-1, 设
??+4
=t(2≤t≤3), 则y=t-
1
5
(t2-4)-1=-
1
5
t2+t-
1
5
=-
1
5
(t-
5
2
)2+
21
20
, 所以t=
5
2
即x=
9
4
时,总收益最大,为
21
20
万. 故投资甲产品
9
4
万元,投资乙产品
11
4
万元,可以使得一年的投资获得最大收益为
21
20
万. 【解析】
(1)由函数y1的图象和y2的图象过点(0,0),(5,1)得到m,a,b的方程组,解方程可得m,a,b,进而得到所求函数解析式; (2)设投资甲产品为x万元,则投资乙产品为(5-x)万元,0≤x≤5,则总收益y=y1+y2,运用换元法和二次函数的最值求法,可得所求最大值和x,5-x的值. 本题考查函数在实际问题中的应用,考查函数的最值求法,注意运用换元法,以及二次函数的最值求法,考查化简运算能力,属于中档题.
19.【答案】解:(1)根据题意,二次函数f(x)=x2-mx-1+m的对称轴为x=
??
2
, 若其在区间[-1,0]上是单调函数, 则有
??
2
≥0或
??
2
≤-1, 解可得:m≤-1或x≥0, 则实数m的取值范围为(-∞,-1]∪[0,+∞); (2)对于函数y=f(2x), 令t=2x,则y=t2-mt+m-1,其对称轴为x=
??
2
, 又由x∈[0,2],则1≤t≤4, ①,当
??
2
≤
5
2
时,即m≤5时,t=4时,y=t2-mt+m-1取得最大值,此时g(m)=16-4m+m-1=15-3m, ②,当
??
2
>
5
2
时,即m>5时,t=1时,y=t2-mt+m-1取得最大值,此时g(m)=1-m+m-1=0, 综合可得:g(m)=
0,??>5
15?3??,??≤5
. 【解析】
(1)根据题意,分析可得f(x)=x2-mx-1+m的对称轴为x=,结合二次函数的性质分析可得答案; (2)令t=2x,则y=t2-mt+m-1,分析t的范围,结合二次函数的性质分2种情况讨论,求出g(m)的解析式,综合可得答案. 本题考查函数的单调性的判断以及换元法分析函数的最值,注意结合二次函数的性质分析,属于基础题.
20.【答案】解:(1)证明:假设f(x)是奇函数, 那么f(-x)=-f(x)对于一切x∈R恒成立, 可得f(0)=0,而f(0)=1+|1-a|≠0,所以函数f(x)不是奇函数; (2)因为3x>0,所以当a≤0时,不等式f(x)>a2可以化为32x+3x-a>a2, 即(3x-a)(3x+a+1)>0,因为3x-a>0,所以3x+a+1>0,即3x>-a-1, ①当a+1≥0,即-1≤a≤0时,不等式3x>-a-1恒成立,故x的取值范围是R. ②当a+1<0,即a<-1时,不等式3x>-a-1得x>log3(-a-1), 故x的取值范围是(log3(-a-1),+∞); (3)令3x=t,则t>0且y=t2+|t-a|. ①若a≤0,则y=t2+t-a是增函数, 其取值范围为(-a,+∞); ②若a>0,则y=
??
2
+?????,??>??
??
2
???+??,0??
, 对于0<t≤a,有y=(t-
1
2
)2+a-
1
4
.当0<a<
1
2
时,y是减函数,取值范围是[a2,a); 当a≥
1
2
时,y的最小值是a-
1
4
,y取值范围是[a-
1
4
,a)(
1
2
≤a<1时) 或者y取值范围是[a-
1
4
,a2](a≥1时) 对于t≥a,有y=(t+
1
2
)2-a-
1
4
是增函数,其取值范围为[a2,+∞). 综上所述,当a≤0时,值域为(-a,+∞); 当0<a<
1
2
时,值域为[a2,+∞); 当a≥
1
2
时,值域为[a-
1
4
,+∞). 【解析】
(1)运用反证法,假设f(x)是奇函数,运用定义法,可得f(0)=0,而f(0)不可能为0,可得证明; (2)讨论a的范围,-1≤a≤0时,a<-1时,运用指数函数的单调性可得解集; (3)令3x=t,则t>0且y=t2+|t-a|.讨论a>0,a≤0,结合二次函数的单调性和对称轴,以及指数函数的值域,即可得到所求值域. 本题考查函数的奇偶性的判断,以及函数的值域的求法,不等式的解法,考查换元法和分类讨论思想方法,以及化简整理的运算能力,属于难题.
同课章节目录
