上海市浦东新区2017-2018学年上学期期末考试八年级数学试题(五四学制)(含答案)
文档属性
| 名称 | 上海市浦东新区2017-2018学年上学期期末考试八年级数学试题(五四学制)(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 203.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-01-11 00:00:00 | ||
图片预览


文档简介
上海市浦东新区2017-2018学年上学期期末考试八年级数学试题(五四学制)
一、选择题(每小题2分,共10分)
1.(2分)在下列代数式中,不是二次根式的是( )
A. B. C. D.
2.(2分)下列两数都是方程x2﹣2x=7+4x的根是( )
A.1,7 B.1,﹣7 C.﹣1,7 D.﹣1,﹣7
3.(2分)如果反比例函数的图象经过点(3,﹣5),那么这个反比例函数的图象一定经过点( )
A.(3,5) B.(﹣3,5) C.(﹣3,﹣5) D.(0,﹣5)
4.(2分)在以下列三个数为边长的三角形中,不能组成直角三角形的是( )
A.4、7、9 B.5、12、13 C.6、8、10 D.7、24、25
5.(2分)在下列四个命题中的逆命题中,是真命题的个数共有( )
①相等的角是对顶角;②等腰三角形腰上的高相等;③直角三角形的两个锐角互余;④全等三角形的三个角分别对应相等.
A.1个 B.2个 C.3个 D.4个
二、填空题(每小题2分,共30分)
6.(2分)的有理化因式为 .
7.(2分)如果二次三项式x2﹣8x+m能配成完全平方式,那么m的值是 .
8.(2分)如果关于x的方程(m﹣1)x3﹣mx2+2=0是一元二次方程,那么此方程的根是 .
9.(2分)如果方程5x2﹣4x=m没有实数根,那么m的取值范围是 .
10.(2分)在实数范围内分解因式:x2﹣3y2= .
11.(2分)函数y=的定义域为 .
12.(2分)已知函数f(x)=,那么f(6)= .
13.(2分)初二(2)班共有38名学生,其中参加读书活动的学生人数为n(1≤n≤38,且n为整数),参与率为p,那么p关于n的函数解析式为 .
14.(2分)已知正比例函数的图象经过点(﹣2,6),那么这个函数中的函数值y随自变量x值的增大而 .
15.(2分)如果点A的坐标为(3,5),点B的坐标为(0,﹣4),那么A、B两点的距离等于 .
16.(2分)已知直线AB上有一点P,那么在直线AB上,且到点P的距离为3厘米的点共有 个.
17.(2分)如图,已知在Rt△ABC中,斜边AB的垂直平分线交边AC于点D,且∠CBD:∠ABD=4:3,那么∠A= 度.
18.(2分)如果等边三角形的边长为m厘米,那么这个三角形的面积等于 平方厘米(用含m的代数式表示).
19.(2分)已知在△ABC中,AB=9,AC=10,BC=17,那么边AB上的高等于 .
20.(2分)已知在平面直角坐标xOy中,正比例函数y=﹣4x的图象经过点A(﹣3,m),点B在x轴的负半轴上,过点A作直线AC∥x轴,交∠AOB的平分线OC于点C,那么点C到直线OA的距离等于 .
三、解答题(本大题共7题,满分60分)
21.(15分)(1)计算:;
(2)解不等式: x≤2x+3;
(3)解方程:3x2+4x﹣1=0.
22.(6分)已知:如图,BD=CD,∠B=∠C,求证:AD平分∠BAC.
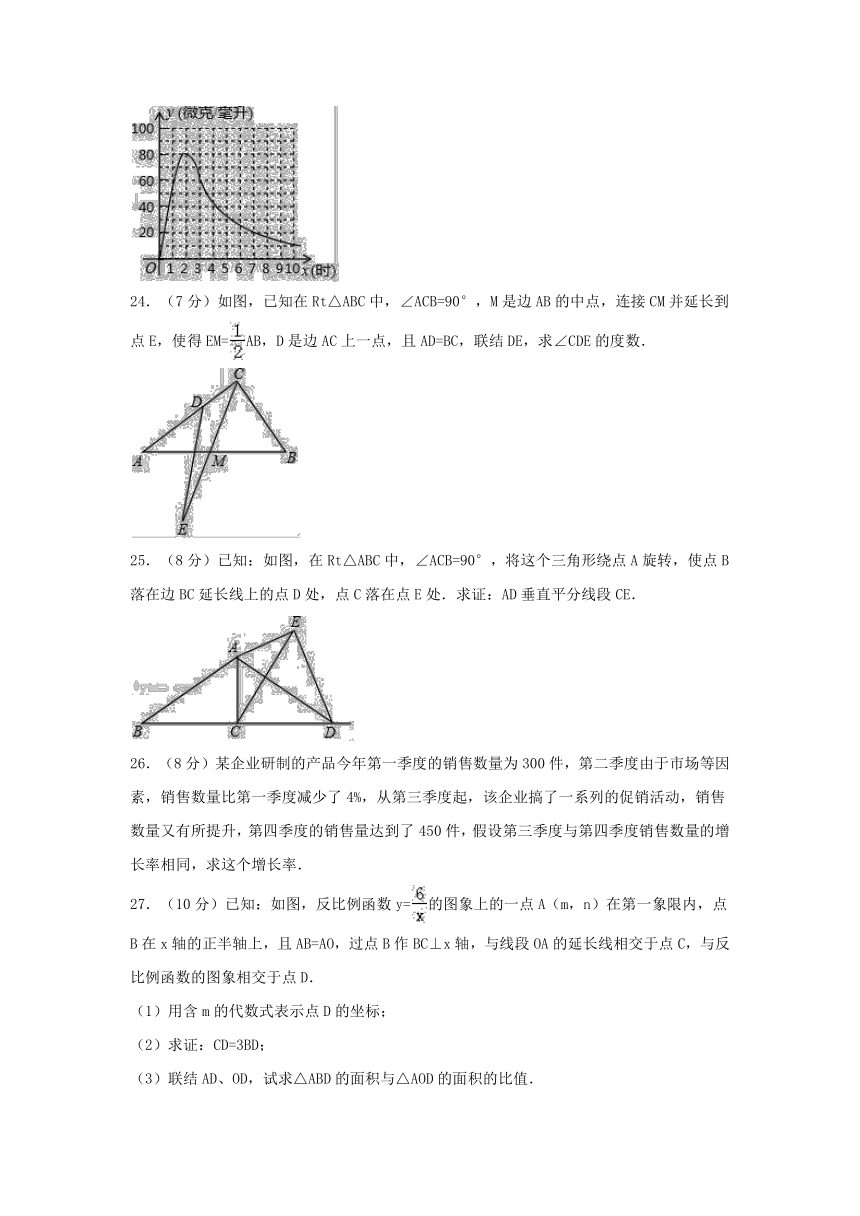
23.(6分)某药物研究单位试制成功一种新药,经测试,如果患者按规定剂量服用,那么服药后每毫升血液中含药量y(微克)随时间x(小时)之间的关系如图所示,如果每毫升血液中的含药量不小于20微克,那么这种药物才能发挥作用,请根据题意回答下列问题:
(1)服药后,大约 分钟后,药物发挥作用.
(2)服药后,大约 小时,每毫升血液中含药量最大,最大值是 微克;
(3)服药后,药物发挥作用的时间大约有 小时.
24.(7分)如图,已知在Rt△ABC中,∠ACB=90°,M是边AB的中点,连接CM并延长到点E,使得EM=AB,D是边AC上一点,且AD=BC,联结DE,求∠CDE的度数.
25.(8分)已知:如图,在Rt△ABC中,∠ACB=90°,将这个三角形绕点A旋转,使点B落在边BC延长线上的点D处,点C落在点E处.求证:AD垂直平分线段CE.
26.(8分)某企业研制的产品今年第一季度的销售数量为300件,第二季度由于市场等因素,销售数量比第一季度减少了4%,从第三季度起,该企业搞了一系列的促销活动,销售数量又有所提升,第四季度的销售量达到了450件,假设第三季度与第四季度销售数量的增长率相同,求这个增长率.
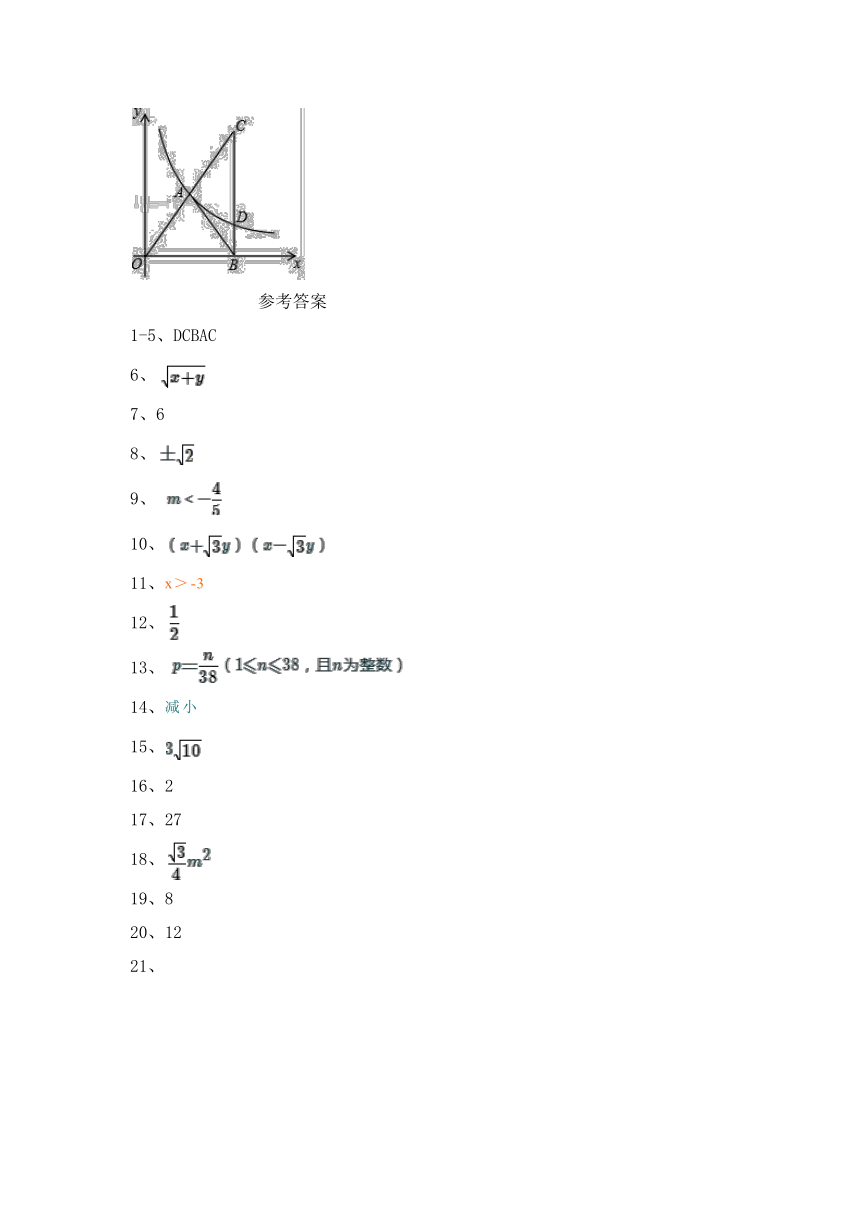
27.(10分)已知:如图,反比例函数y=的图象上的一点A(m,n)在第一象限内,点B在x轴的正半轴上,且AB=AO,过点B作BC⊥x轴,与线段OA的延长线相交于点C,与反比例函数的图象相交于点D.
(1)用含m的代数式表示点D的坐标;
(2)求证:CD=3BD;
(3)联结AD、OD,试求△ABD的面积与△AOD的面积的比值.
参考答案
1-5、DCBAC
6、
7、6
8、
9、
10、
11、x>-3
12、
13、
14、减小
15、
16、2
17、27
18、
19、8
20、12
21、
22、
23、
24、
25、
26、
27、
一、选择题(每小题2分,共10分)
1.(2分)在下列代数式中,不是二次根式的是( )
A. B. C. D.
2.(2分)下列两数都是方程x2﹣2x=7+4x的根是( )
A.1,7 B.1,﹣7 C.﹣1,7 D.﹣1,﹣7
3.(2分)如果反比例函数的图象经过点(3,﹣5),那么这个反比例函数的图象一定经过点( )
A.(3,5) B.(﹣3,5) C.(﹣3,﹣5) D.(0,﹣5)
4.(2分)在以下列三个数为边长的三角形中,不能组成直角三角形的是( )
A.4、7、9 B.5、12、13 C.6、8、10 D.7、24、25
5.(2分)在下列四个命题中的逆命题中,是真命题的个数共有( )
①相等的角是对顶角;②等腰三角形腰上的高相等;③直角三角形的两个锐角互余;④全等三角形的三个角分别对应相等.
A.1个 B.2个 C.3个 D.4个
二、填空题(每小题2分,共30分)
6.(2分)的有理化因式为 .
7.(2分)如果二次三项式x2﹣8x+m能配成完全平方式,那么m的值是 .
8.(2分)如果关于x的方程(m﹣1)x3﹣mx2+2=0是一元二次方程,那么此方程的根是 .
9.(2分)如果方程5x2﹣4x=m没有实数根,那么m的取值范围是 .
10.(2分)在实数范围内分解因式:x2﹣3y2= .
11.(2分)函数y=的定义域为 .
12.(2分)已知函数f(x)=,那么f(6)= .
13.(2分)初二(2)班共有38名学生,其中参加读书活动的学生人数为n(1≤n≤38,且n为整数),参与率为p,那么p关于n的函数解析式为 .
14.(2分)已知正比例函数的图象经过点(﹣2,6),那么这个函数中的函数值y随自变量x值的增大而 .
15.(2分)如果点A的坐标为(3,5),点B的坐标为(0,﹣4),那么A、B两点的距离等于 .
16.(2分)已知直线AB上有一点P,那么在直线AB上,且到点P的距离为3厘米的点共有 个.
17.(2分)如图,已知在Rt△ABC中,斜边AB的垂直平分线交边AC于点D,且∠CBD:∠ABD=4:3,那么∠A= 度.
18.(2分)如果等边三角形的边长为m厘米,那么这个三角形的面积等于 平方厘米(用含m的代数式表示).
19.(2分)已知在△ABC中,AB=9,AC=10,BC=17,那么边AB上的高等于 .
20.(2分)已知在平面直角坐标xOy中,正比例函数y=﹣4x的图象经过点A(﹣3,m),点B在x轴的负半轴上,过点A作直线AC∥x轴,交∠AOB的平分线OC于点C,那么点C到直线OA的距离等于 .
三、解答题(本大题共7题,满分60分)
21.(15分)(1)计算:;
(2)解不等式: x≤2x+3;
(3)解方程:3x2+4x﹣1=0.
22.(6分)已知:如图,BD=CD,∠B=∠C,求证:AD平分∠BAC.
23.(6分)某药物研究单位试制成功一种新药,经测试,如果患者按规定剂量服用,那么服药后每毫升血液中含药量y(微克)随时间x(小时)之间的关系如图所示,如果每毫升血液中的含药量不小于20微克,那么这种药物才能发挥作用,请根据题意回答下列问题:
(1)服药后,大约 分钟后,药物发挥作用.
(2)服药后,大约 小时,每毫升血液中含药量最大,最大值是 微克;
(3)服药后,药物发挥作用的时间大约有 小时.
24.(7分)如图,已知在Rt△ABC中,∠ACB=90°,M是边AB的中点,连接CM并延长到点E,使得EM=AB,D是边AC上一点,且AD=BC,联结DE,求∠CDE的度数.
25.(8分)已知:如图,在Rt△ABC中,∠ACB=90°,将这个三角形绕点A旋转,使点B落在边BC延长线上的点D处,点C落在点E处.求证:AD垂直平分线段CE.
26.(8分)某企业研制的产品今年第一季度的销售数量为300件,第二季度由于市场等因素,销售数量比第一季度减少了4%,从第三季度起,该企业搞了一系列的促销活动,销售数量又有所提升,第四季度的销售量达到了450件,假设第三季度与第四季度销售数量的增长率相同,求这个增长率.
27.(10分)已知:如图,反比例函数y=的图象上的一点A(m,n)在第一象限内,点B在x轴的正半轴上,且AB=AO,过点B作BC⊥x轴,与线段OA的延长线相交于点C,与反比例函数的图象相交于点D.
(1)用含m的代数式表示点D的坐标;
(2)求证:CD=3BD;
(3)联结AD、OD,试求△ABD的面积与△AOD的面积的比值.
参考答案
1-5、DCBAC
6、
7、6
8、
9、
10、
11、x>-3
12、
13、
14、减小
15、
16、2
17、27
18、
19、8
20、12
21、
22、
23、
24、
25、
26、
27、
同课章节目录
