北师大版高中数学必修五:1.2 数列的函数特性 课件
文档属性
| 名称 | 北师大版高中数学必修五:1.2 数列的函数特性 课件 |

|
|
| 格式 | zip | ||
| 文件大小 | 226.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-01-12 00:00:00 | ||
图片预览






文档简介
课件20张PPT。1.2 数列的函数特性1.数列的概念是什么.2.数列的通项公式的含义是什么. 由上节课的学习我们知道数列可以看作定义域为正整数集N+(或它的有限子集)的函数,当自变量从小到大依次取值时,该函数对应的一列函数值就是这个数列. 而数列的通项公式就类似于函数的解析式,因此研究数列的性质我们就可以借助数列的通项公式,而且数列的表示形式也和函数一样,有多种表示方法,下面来看几个例子. 新中国成立后,我国1952~1994年间部分年份进出口贸易总额(亿美元)数据排成一数列:数列的函数特性请看下面例子19.4, 31.0, 42.5, 45.9, 147.5,
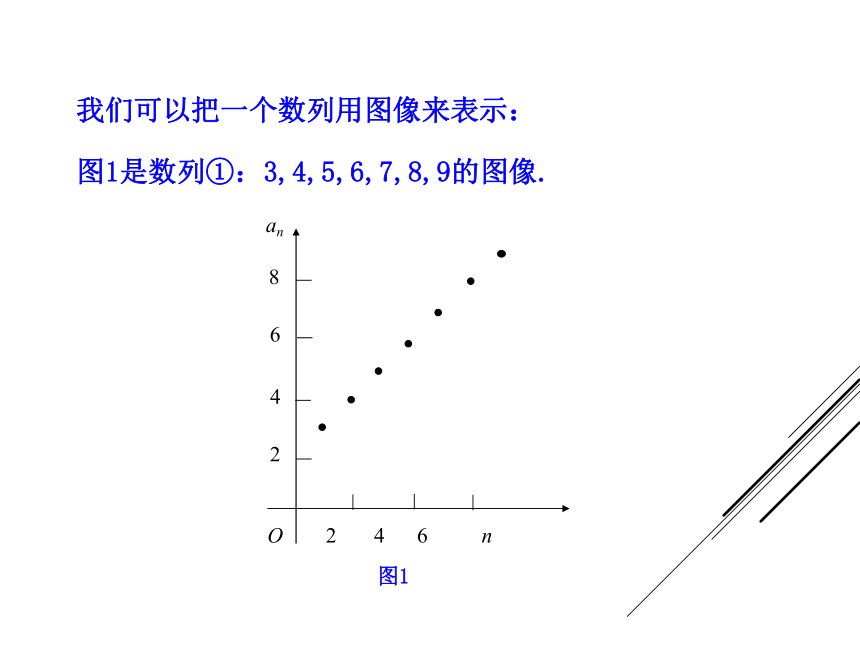
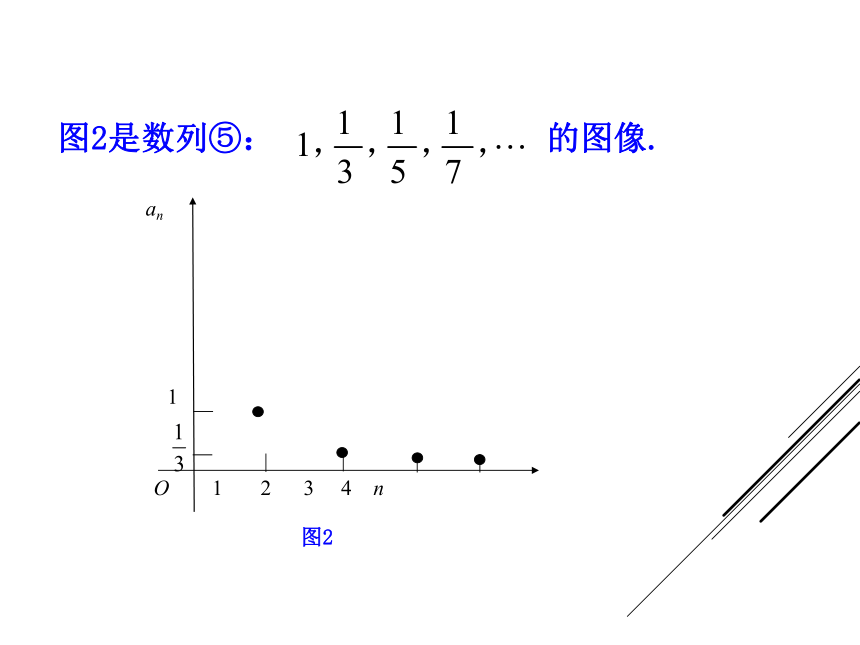
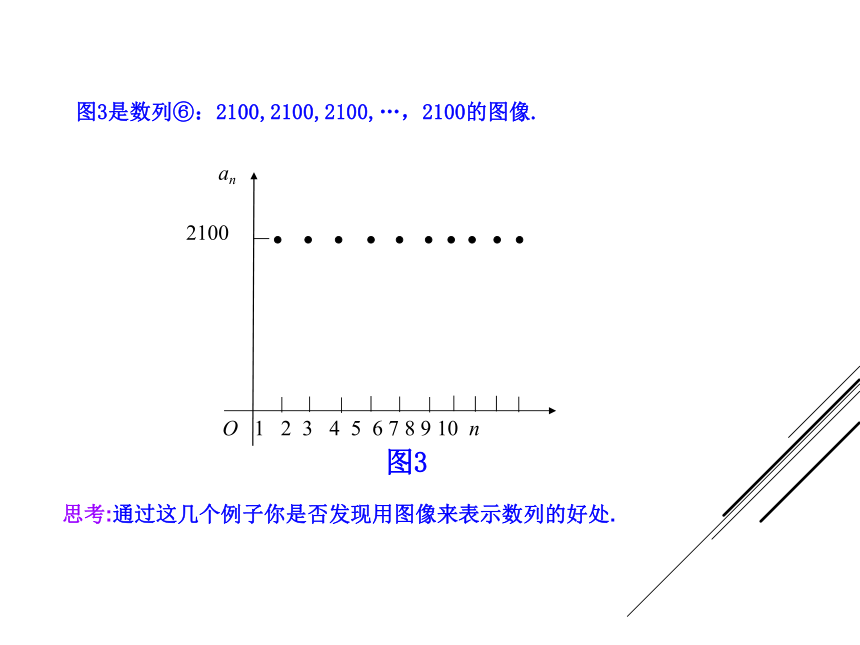
381.4, 696.0, 1 154.4, 2 367.3. 由上图可以看出我国1952~1994年部分年份,各时期进出口贸易总额的增长变化情况.贸易总额/亿美元年份/年我们可以把一个数列用图像来表示:图1是数列①:3,4,5,6,7,8,9的图像.O 2 4 6 n图2是数列⑤: 的图像.图3是数列⑥:2100,2100,2100,…,2100的图像.思考:通过这几个例子你是否发现用图像来表示数列的好处. 从图中可以看出,数列①的函数图像上升,称这样的数列为递增数列;数列⑤的函数图像下降,称这样的数列为递减数列;数列⑥称为常数列.思考:你是否能归纳一下递增数列、递减数列、常数列的概念呢? 一般地,一个数列{an},如果从第2项起,每一项都大于它前面的一项,即an+1> an,那么这个数列叫作递增数列. 如果从第2项起,每一项都小于它前面的一项,即an+1可见,我们也可以用1.判断下列数列的增减性. 本节课主要学习了:
1.递增数列、递减数列、常数列.
2.判断数列增减性的方法.
3.数列是一类定义域为正整数集的特殊函数,它也可以用图像、表格表示.作业:教材P8习题1-1 5.6
写在作业本上.
381.4, 696.0, 1 154.4, 2 367.3. 由上图可以看出我国1952~1994年部分年份,各时期进出口贸易总额的增长变化情况.贸易总额/亿美元年份/年我们可以把一个数列用图像来表示:图1是数列①:3,4,5,6,7,8,9的图像.O 2 4 6 n图2是数列⑤: 的图像.图3是数列⑥:2100,2100,2100,…,2100的图像.思考:通过这几个例子你是否发现用图像来表示数列的好处. 从图中可以看出,数列①的函数图像上升,称这样的数列为递增数列;数列⑤的函数图像下降,称这样的数列为递减数列;数列⑥称为常数列.思考:你是否能归纳一下递增数列、递减数列、常数列的概念呢? 一般地,一个数列{an},如果从第2项起,每一项都大于它前面的一项,即an+1> an,那么这个数列叫作递增数列. 如果从第2项起,每一项都小于它前面的一项,即an+1
1.递增数列、递减数列、常数列.
2.判断数列增减性的方法.
3.数列是一类定义域为正整数集的特殊函数,它也可以用图像、表格表示.作业:教材P8习题1-1 5.6
写在作业本上.
