北师大版高中数学必修五:2.2 三角形中的几何计算 课件(18张)
文档属性
| 名称 | 北师大版高中数学必修五:2.2 三角形中的几何计算 课件(18张) |

|
|
| 格式 | zip | ||
| 文件大小 | 964.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-01-12 21:41:33 | ||
图片预览






文档简介
课件18张PPT。掌握三角形的面积公式.
会用正、余弦定理计算三角形中的一些量.
§2 三角形中的几何计算【课标要求】
【核心扫描】
计算三角形的面积.(重点)
利用面积公式、正余弦定理及三角函数公式求解综合题.(难点)
1.2.1.2.(2)若cos A=cos B,则A___B;
(3)若a2>b2+c2,则△ABC为___________;
(4)若a2=b2+c2,则△ABC为___________ ;
(5)若a2_____.
想一想:解三角形的“归一”思想是什么?
提示 由于几何体的复杂性,导致了运用的难度,在众多的角度和边长问题中,要采用“归一”思想,即归到一个三角形内计算,需要什么就在其他三角形中求什么.
=钝角三角形直角三角形锐角三角形 题型一 计算三角形的面积[思路探索] 利用三角函数公式求A,再结合条件列方程求bc,利用面积公式求S△ABC.
【例1】规律方法 求三角形的面积,要充分挖掘题目中的条件,转化为求两边或两边之积及其夹角正弦的问题,要注意方程思想在解题中的应用.另外也要注意三个内角的取值范围,以避免由三角函数值求角时出现增根错误.
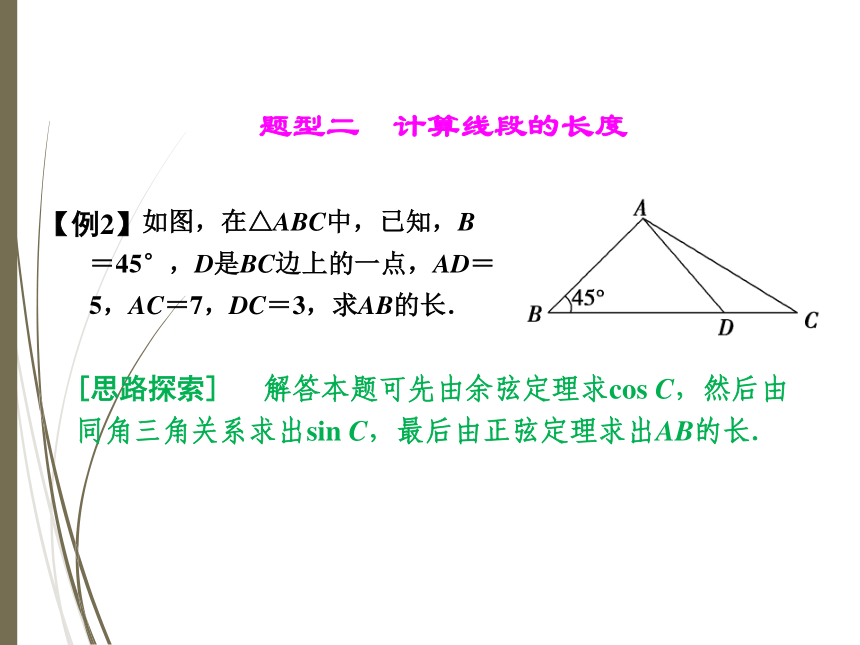
【训练1】 如图,在△ABC中,已知,B=45°,D是BC边上的一点,AD=5,AC=7,DC=3,求AB的长.
【例2】题型二 计算线段的长度[思路探索] 解答本题可先由余弦定理求cos C,然后由同角三角关系求出sin C,最后由正弦定理求出AB的长.
规律方法 有关线段的长度问题往往归结为求解三角形的边长,求三角形边长的问题一般会涉及正、余弦定理,恰当地选择正弦或余弦定理是解这类问题的关键.
已知AB⊥BD,AC⊥CD,AC=1,AB=2,∠BAC=120°,求BD的长.
【训练2】(1)求角C的大小;
(2)求sin A+sin B的最大值.
审题指导 本题考查了余弦定理、三角形面积公式、三角恒等变换等基础知识,同时考查了三角运算求解能力.
【例3】 题型三 三角形中的综合问题【题后反思】 此类问题常以三角形为载体,以正、余弦定理和三角函数公式为工具来综合考查,因此要掌握正、余弦定理,掌握三角函数的公式和性质.
【训练3】 △ABC中,sin 2A=sin 2B,则△ABC的形状是( ).
A.等腰三角形 B.等腰直角三角形
C.等腰或直角三角形 D.直角三角形
[错解] 选A、B.误区警示 忽视角之间的关系而致错
【示例】变式练习:如图,已知在四边形ABCD中,AD⊥CD,AD=10,AB=14,∠BDA=60°,∠BCD=135°,求BC 的长.
分析:在△ABD中,已知两边和其中一边的对角,用正弦定理可求出另一边的对角,但得不到其与△BCD的联系,可再考虑用余弦定理求出BD,其恰好是两个三角形的公共边,这样可在△BCD中应用正弦定理求BC.
会用正、余弦定理计算三角形中的一些量.
§2 三角形中的几何计算【课标要求】
【核心扫描】
计算三角形的面积.(重点)
利用面积公式、正余弦定理及三角函数公式求解综合题.(难点)
1.2.1.2.(2)若cos A=cos B,则A___B;
(3)若a2>b2+c2,则△ABC为___________;
(4)若a2=b2+c2,则△ABC为___________ ;
(5)若a2
想一想:解三角形的“归一”思想是什么?
提示 由于几何体的复杂性,导致了运用的难度,在众多的角度和边长问题中,要采用“归一”思想,即归到一个三角形内计算,需要什么就在其他三角形中求什么.
=钝角三角形直角三角形锐角三角形 题型一 计算三角形的面积[思路探索] 利用三角函数公式求A,再结合条件列方程求bc,利用面积公式求S△ABC.
【例1】规律方法 求三角形的面积,要充分挖掘题目中的条件,转化为求两边或两边之积及其夹角正弦的问题,要注意方程思想在解题中的应用.另外也要注意三个内角的取值范围,以避免由三角函数值求角时出现增根错误.
【训练1】 如图,在△ABC中,已知,B=45°,D是BC边上的一点,AD=5,AC=7,DC=3,求AB的长.
【例2】题型二 计算线段的长度[思路探索] 解答本题可先由余弦定理求cos C,然后由同角三角关系求出sin C,最后由正弦定理求出AB的长.
规律方法 有关线段的长度问题往往归结为求解三角形的边长,求三角形边长的问题一般会涉及正、余弦定理,恰当地选择正弦或余弦定理是解这类问题的关键.
已知AB⊥BD,AC⊥CD,AC=1,AB=2,∠BAC=120°,求BD的长.
【训练2】(1)求角C的大小;
(2)求sin A+sin B的最大值.
审题指导 本题考查了余弦定理、三角形面积公式、三角恒等变换等基础知识,同时考查了三角运算求解能力.
【例3】 题型三 三角形中的综合问题【题后反思】 此类问题常以三角形为载体,以正、余弦定理和三角函数公式为工具来综合考查,因此要掌握正、余弦定理,掌握三角函数的公式和性质.
【训练3】 △ABC中,sin 2A=sin 2B,则△ABC的形状是( ).
A.等腰三角形 B.等腰直角三角形
C.等腰或直角三角形 D.直角三角形
[错解] 选A、B.误区警示 忽视角之间的关系而致错
【示例】变式练习:如图,已知在四边形ABCD中,AD⊥CD,AD=10,AB=14,∠BDA=60°,∠BCD=135°,求BC 的长.
分析:在△ABD中,已知两边和其中一边的对角,用正弦定理可求出另一边的对角,但得不到其与△BCD的联系,可再考虑用余弦定理求出BD,其恰好是两个三角形的公共边,这样可在△BCD中应用正弦定理求BC.
