苏科版九年级上期末专题:第一章一元二次方程(含答案)
文档属性
| 名称 | 苏科版九年级上期末专题:第一章一元二次方程(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 54.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-01-12 23:43:18 | ||
图片预览


文档简介
苏科版九年级数学上册期末专题: 第一章 一元二次方程
一、单选题(共10题;共30分)
1.一元二次方程x2+x﹣6=0的根的情况是(? )
A.?有两个相等的实根????????????????B.?没有实数根????????????????C.?有两个不相等的实根????????????????D.?无法确定
2.下列方程中,没有实数根的是(?? )
A.?x2﹣4x+4=0?????????????????????B.?x2﹣2x+5=0?????????????????????C.?x2﹣2x=0?????????????????????D.?x2﹣2x﹣3=0
3.一个多边形有9条对角线,则这个多边形的边数是(??? )
A.?5???????????????????????????????????????????/B.?6???????????????????????????????????????????/C.?7???????????????????????????????????????????/D.?8
4.已知方程x2+bx+a=0有一个根是-a(a≠0),则下列代数式的值恒为常数的是( )
A.?ab???????????????????????????????????????/B.?
??
??
???????????????????????????????????????/C.?a+b???????????????????????????????????????/D.?a-b
5.用配方法解方程x2+8x+7=0,则配方正确的是( )
A.?
??+4
2
=9??????????????????/B.?
???4
2
=9??????????????????/C.?
???8
2
=16??????????????????/D.?
??+8
2
=57
6.如图,将边长为2cm的正方形ABCD沿其对角线AC剪开,再把△ABC沿着AD方向平移,得到△A′B′C′,若两个三角形重叠部分的面积为1cm2 , 则它移动的距离AA′等于( ) /
A.?0.5cm???????????????????????????????????B.?1cm???????????????????????????????????C.?1.5cm???????????????????????????????????D.?2cm
7.关于 ?? 的方程
??
2
+(??
2
?
4)??+??+1=0 的两个根互为相反数,则 ?? 值是(?????? )
A.??1????????????????????????????????????????/B.?±2????????????????????????????????????????/C.?2????????????????????????????????????????/D.??2
8.如果一元二次方程x2+12x+27=0的两个根是x1 , x2 , 那么x1+x2的值为( )
A.?-6???????????????????????????????????????/B.?-12???????????????????????????????????????/C.?12???????????????????????????????????????/D.?27
9.若关于x的一元二次方程mx2﹣x=
1
4
有实数根,则实数m的取值范围是(?? )
A.m≥﹣1 B.m≥﹣1且m≠0 C.m>﹣1且m≠0 D.m≠0
10.若关于x的方程x2+(2k+1)x-2+k2=0有实数根,则k的取值范围是 (?? )
A.?k<
9
4
???????????????????????????????????B.?k≤-
9
4
???????????????????????????????????C.?k>
9
4
???????????????????????????????????D.?k≥-
9
4
二、填空题(共10题;共30分)
11.方程(x﹣3)2=x﹣3的根是________.
12.若关于x的一元二次方程ax2﹣bx+2=0(a≠0)的一个解是x=1,则3﹣a+b的值是________.
13.一元二次方程
??
2
?3??+1=0 根的判别式的值为________.
14.方程(x﹣3)(x﹣9)=0的根是________.
15.方程4x2﹣kx+6=0的一个根是2,那么k=________?
16.已知x1=3是关于x的一元二次方程x2-4x+c=0的一个根,则方程的另一个根x2是________。
17.若关于x的方程x2+2(k﹣1)x+k2=0有实数根,则k的取值范围是________.
18.关于x的一元二次方程(a-1)x2-2x+3=0有实数根,则整数a的最大值是________.
19.若方程(m+2)x|m|+3mx+1=0是关于x的一元二次方程,则m=________.
20.在△ABC中,已知两边a=3,b=4,第三边为c.若关于x的方程
??
2
+(???4)??+
1
4
=0 有两个相等的实数根,则该三角形的面积是________
三、解答题(共7题;共60分)
21.用配方法解方程:2x2﹣4x﹣1=0.
22.当m是何值时,关于x的方程(m2+2)x2+(m﹣1)x﹣4=3x2 (1)是一元二次方程; (2)是一元一次方程; (3)若x=﹣2是它的一个根,求m的值.
23.某商场要经营一种新上市的文具,进价为20元,试营销阶段发现:当销售单价是25元时,每天的销售量为250件,销售单价每上涨1元,每天的销售量就减少10件. ①写出商场销售这种文具,每天所得的销售利润w(元)与销售单价x(元)之间的函数关系式,并写出x的取值范围. ②若商场要每天获得销售利润2000元,销售单价应定为多少元? ③求销售单价为多少元时,该文具每天的销售利润最大?最大利润是多少?
24.某汽车销售公司2月份销售新上市一种新型低能耗汽车20辆,由于该型汽车的优越的经济适用性,销量快速上升,4月份该公司销售该型汽车达45辆. (1)求该公司销售该型汽车3月份和4月份的平均增长率; (2)该型汽车每辆的进价为10万元;且销售a辆汽车,汽车厂返利销售公司0.03a万元/辆,该公司的该型车售价为11万元/辆,若使5月份每辆车盈利不低于2.6万元,那么该公司5月份至少需要销售该型汽车多少辆?此时总盈利至少是多少万元?(盈利=销售利润+返利)
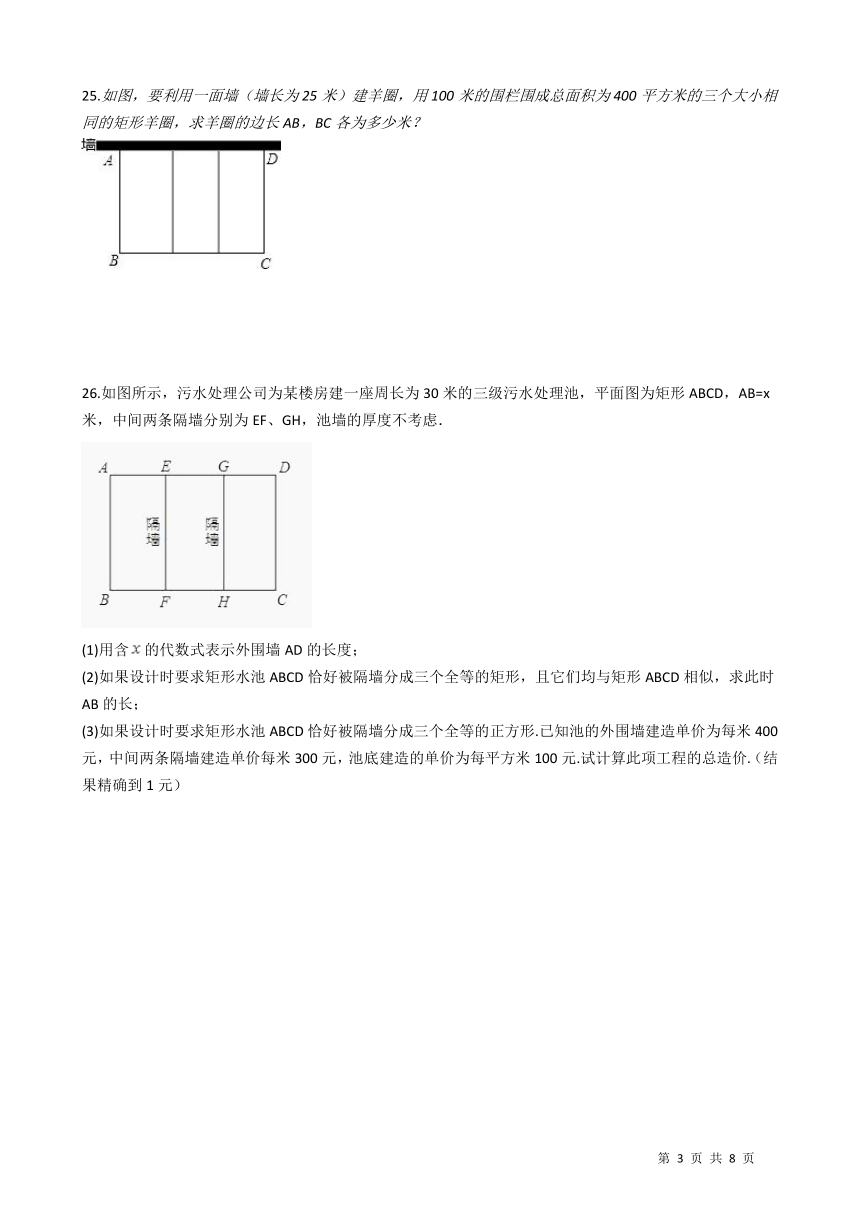
25.如图,要利用一面墙(墙长为25米)建羊圈,用100米的围栏围成总面积为400平方米的三个大小相同的矩形羊圈,求羊圈的边长AB,BC各为多少米? /
26.如图所示,污水处理公司为某楼房建一座周长为30米的三级污水处理池,平面图为矩形ABCD,AB=x米,中间两条隔墙分别为EF、GH,池墙的厚度不考虑. / (1)用含/的代数式表示外围墙AD的长度; (2)如果设计时要求矩形水池ABCD恰好被隔墙分成三个全等的矩形,且它们均与矩形ABCD相似,求此时AB的长; (3)如果设计时要求矩形水池ABCD恰好被隔墙分成三个全等的正方形.已知池的外围墙建造单价为每米400元,中间两条隔墙建造单价每米300元,池底建造的单价为每平方米100元.试计算此项工程的总造价.(结果精确到1元)
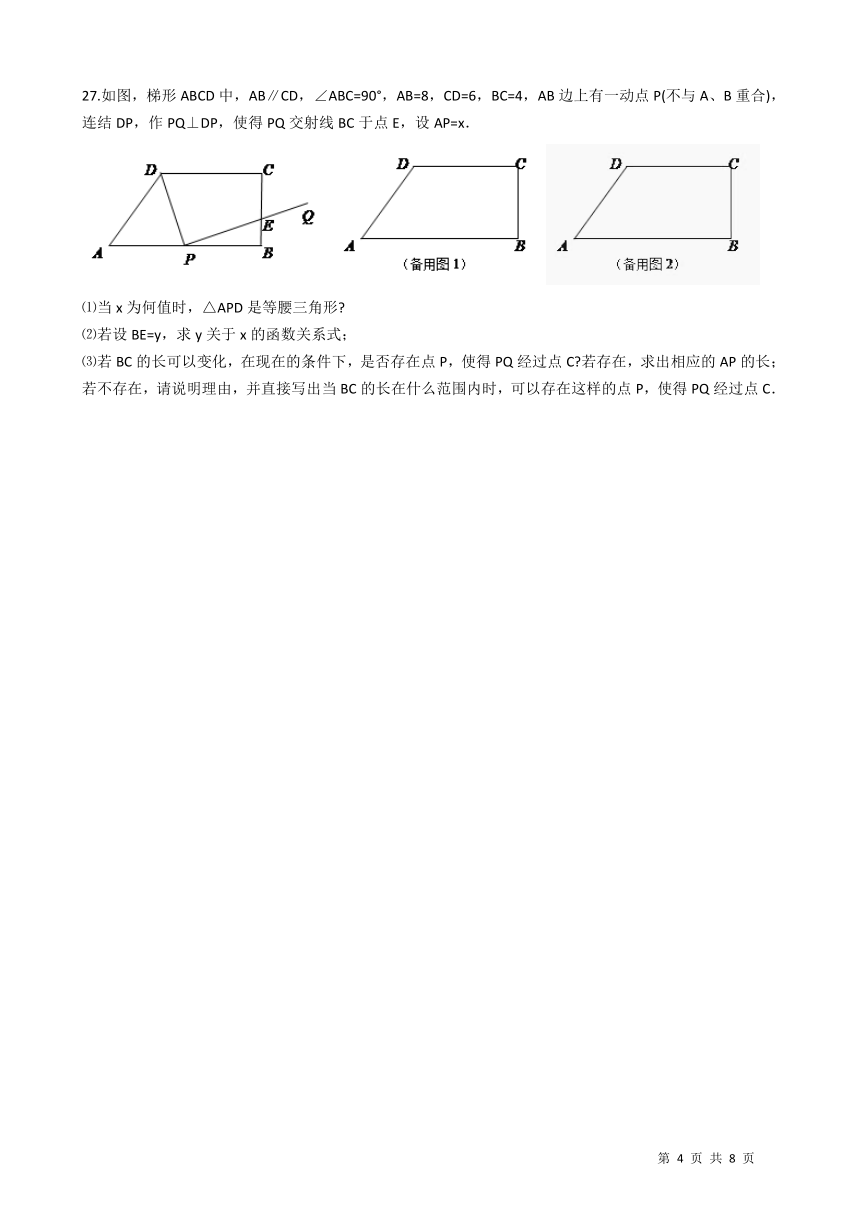
27.如图,梯形ABCD中,AB∥CD,∠ABC=90°,AB=8,CD=6,BC=4,AB边上有一动点P(不与A、B重合),连结DP,作PQ⊥DP,使得PQ交射线BC于点E,设AP=x. /// ⑴当x为何值时,△APD是等腰三角形? ⑵若设BE=y,求y关于x的函数关系式; ⑶若BC的长可以变化,在现在的条件下,是否存在点P,使得PQ经过点C?若存在,求出相应的AP的长;若不存在,请说明理由,并直接写出当BC的长在什么范围内时,可以存在这样的点P,使得PQ经过点C.
答案解析部分
一、单选题
1.【答案】C
2.【答案】B
3.【答案】B
4.【答案】D
5.【答案】A
6.【答案】B
7.【答案】D
8.【答案】B
9.【答案】B
10.【答案】D
二、填空题
11.【答案】x1=3,x2=4
12.【答案】5
13.【答案】5
14.【答案】x1=3,x2=9
15.【答案】11
16.【答案】1
17.【答案】k≤
1
2
18.【答案】0
19.【答案】2
20.【答案】6或 2
5
三、解答题
21.【答案】解:2x2﹣4x﹣1=0,
2x2﹣4x=1,
x2﹣2x=
1
2
,
配方得:x2﹣2x+1=
1
2
+1,
(x﹣1)2=
3
2
,
开方得:x﹣1=±
3
2
,
解得:x1=
2+
6
2
,x2=
2?
6
2
.
22.【答案】?解:原方程可化为(m2﹣1)x2+(m﹣1)x﹣4=0, (1)当m2﹣1≠0,即m≠±1时,是一元二次方程; (2)当m2﹣1=0,且m﹣1≠0,即m=﹣1时,是一元一次方程; (3)x=﹣2时,原方程化为:2m2﹣m﹣3=0, 解得,m1=
2
3
, m2=﹣1(舍去).
23.【答案】解:①w=(x﹣20)[250﹣10(x﹣25)] =(x﹣20)(﹣10x+500) =﹣10x2+700x﹣10000( 25≤x≤50 ); ②当w=2000时,得﹣10x2+700x﹣10000=2000 解得:x1=30,x2=40, 所以,商场要每天获得销售利润2000元,销售单价应定为30元或40元; ③w=﹣10x2+700x﹣10000=﹣10(x﹣35)2+2250. ∵﹣10<0, ∴函数图象开口向下,w有最大值, 当x=35时,wmax=2250, 故当单价为35元时,该文具每天的利润最大,最大利润为2250元
24.【答案】解:(1)设该公司销售该型汽车3月份和4月份的平均增长率为x, 根据题意列方程:20(1+x)2=45, 解得x1=﹣250%(不合题意,舍去),x2=50%. 答:该公司销售该型汽车3月份和4月份的平均增长率为50%. (2)由题意得: 0.03a+(11﹣10)≥2.6, 解得:a≥53
1
3
, ∵a为整数, ∴该公司5月份至少需要销售该型汽车54辆, (11﹣10)×54+0.03×54×54=141.48(万元). 答:该公司5月份至少需要销售该型汽车54辆,此时总盈利至少是141.48万元.
25.【答案】解:设AB的长度为x,则BC的长度为(100﹣4x)米.根据题意得 : (100﹣4x)x=400, 解得 x1=20,x2=5. 则100﹣4x=20或100﹣4x=80. ∵80>25, ∴x2=5舍去. 即AB=20,BC=20. 答:羊圈的边长AB,BC分别是20米、20米
26.【答案】解:(1)由题意可知矩形的周长为30米,????=??,所以
????
????
=
????
????
,即??
??
2
=????·????且????=
1
3
???? 解得:
??
1
=
?15+15
3
2
,
??
2
=
?15?15
3
2
, , (不合题意,舍去) ∴?????=
?15+15
3
2
, (3)由题意知????=3??米,则有15???=3?? 解得???=3.75 总造价:=400×30+300×2??+1003??.0??=12000+600??+300
??
2
当时,原式=300×3.
75
2
+600×3.75+12000≈18469 答:此项工程的总造价约为18469元.
27.【答案】解:(1)过D点作DH⊥AB于H,则四边形DHBC为矩形, / ∴DH=BC=4,HB=CD=6. ∴AH=2,AD=2
5
. ∵AP=x, ∴PH=x﹣2, 情况①:当AP=AD时,即x=2
5
. 情况②:当AD=PD时,则AH=PH. ∴2=x﹣2,解得x=4. 情况③:当AP=PD时, 则Rt△DPH中,x2=42+(x﹣2)2 , 解得x=5. ∵2<x<8, ∴当x为2
5
、4、5时,△APD是等腰三角形. (2)∵∠DPE=∠DHP=90°, ∴∠DPH+∠EPB=∠DPH+∠HDP=90°. ∴∠HDP=∠EPB. 又∵∠DHP=∠B=90°, ∴△DPH∽△PEB. ∴
????
????
=
????
????
, ∴
4
???2
=
8???
??
. 整理得:y=
1
4
(x﹣2)(8﹣x)=﹣
1
4
x2+
5
2
x﹣4; (3)存在. 设BC=a,则由(2)得△DPH∽△PEB, ∴
??
8???
=
???2
??
, ∴y=
8???
???2
??
, 当y=a时, (8﹣x)(x﹣2)=a2 x2﹣10x+(16+a2)=0, ∴△=100﹣4(16+a2), ∵△≥0, ∴100﹣64﹣4a2≥0, 4a2≤36, 又∵a>0, ∴a≤3, ∴0<a≤3, ∴满足0<BC≤3时,存在点P,使得PQ经过C.
一、单选题(共10题;共30分)
1.一元二次方程x2+x﹣6=0的根的情况是(? )
A.?有两个相等的实根????????????????B.?没有实数根????????????????C.?有两个不相等的实根????????????????D.?无法确定
2.下列方程中,没有实数根的是(?? )
A.?x2﹣4x+4=0?????????????????????B.?x2﹣2x+5=0?????????????????????C.?x2﹣2x=0?????????????????????D.?x2﹣2x﹣3=0
3.一个多边形有9条对角线,则这个多边形的边数是(??? )
A.?5???????????????????????????????????????????/B.?6???????????????????????????????????????????/C.?7???????????????????????????????????????????/D.?8
4.已知方程x2+bx+a=0有一个根是-a(a≠0),则下列代数式的值恒为常数的是( )
A.?ab???????????????????????????????????????/B.?
??
??
???????????????????????????????????????/C.?a+b???????????????????????????????????????/D.?a-b
5.用配方法解方程x2+8x+7=0,则配方正确的是( )
A.?
??+4
2
=9??????????????????/B.?
???4
2
=9??????????????????/C.?
???8
2
=16??????????????????/D.?
??+8
2
=57
6.如图,将边长为2cm的正方形ABCD沿其对角线AC剪开,再把△ABC沿着AD方向平移,得到△A′B′C′,若两个三角形重叠部分的面积为1cm2 , 则它移动的距离AA′等于( ) /
A.?0.5cm???????????????????????????????????B.?1cm???????????????????????????????????C.?1.5cm???????????????????????????????????D.?2cm
7.关于 ?? 的方程
??
2
+(??
2
?
4)??+??+1=0 的两个根互为相反数,则 ?? 值是(?????? )
A.??1????????????????????????????????????????/B.?±2????????????????????????????????????????/C.?2????????????????????????????????????????/D.??2
8.如果一元二次方程x2+12x+27=0的两个根是x1 , x2 , 那么x1+x2的值为( )
A.?-6???????????????????????????????????????/B.?-12???????????????????????????????????????/C.?12???????????????????????????????????????/D.?27
9.若关于x的一元二次方程mx2﹣x=
1
4
有实数根,则实数m的取值范围是(?? )
A.m≥﹣1 B.m≥﹣1且m≠0 C.m>﹣1且m≠0 D.m≠0
10.若关于x的方程x2+(2k+1)x-2+k2=0有实数根,则k的取值范围是 (?? )
A.?k<
9
4
???????????????????????????????????B.?k≤-
9
4
???????????????????????????????????C.?k>
9
4
???????????????????????????????????D.?k≥-
9
4
二、填空题(共10题;共30分)
11.方程(x﹣3)2=x﹣3的根是________.
12.若关于x的一元二次方程ax2﹣bx+2=0(a≠0)的一个解是x=1,则3﹣a+b的值是________.
13.一元二次方程
??
2
?3??+1=0 根的判别式的值为________.
14.方程(x﹣3)(x﹣9)=0的根是________.
15.方程4x2﹣kx+6=0的一个根是2,那么k=________?
16.已知x1=3是关于x的一元二次方程x2-4x+c=0的一个根,则方程的另一个根x2是________。
17.若关于x的方程x2+2(k﹣1)x+k2=0有实数根,则k的取值范围是________.
18.关于x的一元二次方程(a-1)x2-2x+3=0有实数根,则整数a的最大值是________.
19.若方程(m+2)x|m|+3mx+1=0是关于x的一元二次方程,则m=________.
20.在△ABC中,已知两边a=3,b=4,第三边为c.若关于x的方程
??
2
+(???4)??+
1
4
=0 有两个相等的实数根,则该三角形的面积是________
三、解答题(共7题;共60分)
21.用配方法解方程:2x2﹣4x﹣1=0.
22.当m是何值时,关于x的方程(m2+2)x2+(m﹣1)x﹣4=3x2 (1)是一元二次方程; (2)是一元一次方程; (3)若x=﹣2是它的一个根,求m的值.
23.某商场要经营一种新上市的文具,进价为20元,试营销阶段发现:当销售单价是25元时,每天的销售量为250件,销售单价每上涨1元,每天的销售量就减少10件. ①写出商场销售这种文具,每天所得的销售利润w(元)与销售单价x(元)之间的函数关系式,并写出x的取值范围. ②若商场要每天获得销售利润2000元,销售单价应定为多少元? ③求销售单价为多少元时,该文具每天的销售利润最大?最大利润是多少?
24.某汽车销售公司2月份销售新上市一种新型低能耗汽车20辆,由于该型汽车的优越的经济适用性,销量快速上升,4月份该公司销售该型汽车达45辆. (1)求该公司销售该型汽车3月份和4月份的平均增长率; (2)该型汽车每辆的进价为10万元;且销售a辆汽车,汽车厂返利销售公司0.03a万元/辆,该公司的该型车售价为11万元/辆,若使5月份每辆车盈利不低于2.6万元,那么该公司5月份至少需要销售该型汽车多少辆?此时总盈利至少是多少万元?(盈利=销售利润+返利)
25.如图,要利用一面墙(墙长为25米)建羊圈,用100米的围栏围成总面积为400平方米的三个大小相同的矩形羊圈,求羊圈的边长AB,BC各为多少米? /
26.如图所示,污水处理公司为某楼房建一座周长为30米的三级污水处理池,平面图为矩形ABCD,AB=x米,中间两条隔墙分别为EF、GH,池墙的厚度不考虑. / (1)用含/的代数式表示外围墙AD的长度; (2)如果设计时要求矩形水池ABCD恰好被隔墙分成三个全等的矩形,且它们均与矩形ABCD相似,求此时AB的长; (3)如果设计时要求矩形水池ABCD恰好被隔墙分成三个全等的正方形.已知池的外围墙建造单价为每米400元,中间两条隔墙建造单价每米300元,池底建造的单价为每平方米100元.试计算此项工程的总造价.(结果精确到1元)
27.如图,梯形ABCD中,AB∥CD,∠ABC=90°,AB=8,CD=6,BC=4,AB边上有一动点P(不与A、B重合),连结DP,作PQ⊥DP,使得PQ交射线BC于点E,设AP=x. /// ⑴当x为何值时,△APD是等腰三角形? ⑵若设BE=y,求y关于x的函数关系式; ⑶若BC的长可以变化,在现在的条件下,是否存在点P,使得PQ经过点C?若存在,求出相应的AP的长;若不存在,请说明理由,并直接写出当BC的长在什么范围内时,可以存在这样的点P,使得PQ经过点C.
答案解析部分
一、单选题
1.【答案】C
2.【答案】B
3.【答案】B
4.【答案】D
5.【答案】A
6.【答案】B
7.【答案】D
8.【答案】B
9.【答案】B
10.【答案】D
二、填空题
11.【答案】x1=3,x2=4
12.【答案】5
13.【答案】5
14.【答案】x1=3,x2=9
15.【答案】11
16.【答案】1
17.【答案】k≤
1
2
18.【答案】0
19.【答案】2
20.【答案】6或 2
5
三、解答题
21.【答案】解:2x2﹣4x﹣1=0,
2x2﹣4x=1,
x2﹣2x=
1
2
,
配方得:x2﹣2x+1=
1
2
+1,
(x﹣1)2=
3
2
,
开方得:x﹣1=±
3
2
,
解得:x1=
2+
6
2
,x2=
2?
6
2
.
22.【答案】?解:原方程可化为(m2﹣1)x2+(m﹣1)x﹣4=0, (1)当m2﹣1≠0,即m≠±1时,是一元二次方程; (2)当m2﹣1=0,且m﹣1≠0,即m=﹣1时,是一元一次方程; (3)x=﹣2时,原方程化为:2m2﹣m﹣3=0, 解得,m1=
2
3
, m2=﹣1(舍去).
23.【答案】解:①w=(x﹣20)[250﹣10(x﹣25)] =(x﹣20)(﹣10x+500) =﹣10x2+700x﹣10000( 25≤x≤50 ); ②当w=2000时,得﹣10x2+700x﹣10000=2000 解得:x1=30,x2=40, 所以,商场要每天获得销售利润2000元,销售单价应定为30元或40元; ③w=﹣10x2+700x﹣10000=﹣10(x﹣35)2+2250. ∵﹣10<0, ∴函数图象开口向下,w有最大值, 当x=35时,wmax=2250, 故当单价为35元时,该文具每天的利润最大,最大利润为2250元
24.【答案】解:(1)设该公司销售该型汽车3月份和4月份的平均增长率为x, 根据题意列方程:20(1+x)2=45, 解得x1=﹣250%(不合题意,舍去),x2=50%. 答:该公司销售该型汽车3月份和4月份的平均增长率为50%. (2)由题意得: 0.03a+(11﹣10)≥2.6, 解得:a≥53
1
3
, ∵a为整数, ∴该公司5月份至少需要销售该型汽车54辆, (11﹣10)×54+0.03×54×54=141.48(万元). 答:该公司5月份至少需要销售该型汽车54辆,此时总盈利至少是141.48万元.
25.【答案】解:设AB的长度为x,则BC的长度为(100﹣4x)米.根据题意得 : (100﹣4x)x=400, 解得 x1=20,x2=5. 则100﹣4x=20或100﹣4x=80. ∵80>25, ∴x2=5舍去. 即AB=20,BC=20. 答:羊圈的边长AB,BC分别是20米、20米
26.【答案】解:(1)由题意可知矩形的周长为30米,????=??,所以
????
????
=
????
????
,即??
??
2
=????·????且????=
1
3
???? 解得:
??
1
=
?15+15
3
2
,
??
2
=
?15?15
3
2
, , (不合题意,舍去) ∴?????=
?15+15
3
2
, (3)由题意知????=3??米,则有15???=3?? 解得???=3.75 总造价:=400×30+300×2??+1003??.0??=12000+600??+300
??
2
当时,原式=300×3.
75
2
+600×3.75+12000≈18469 答:此项工程的总造价约为18469元.
27.【答案】解:(1)过D点作DH⊥AB于H,则四边形DHBC为矩形, / ∴DH=BC=4,HB=CD=6. ∴AH=2,AD=2
5
. ∵AP=x, ∴PH=x﹣2, 情况①:当AP=AD时,即x=2
5
. 情况②:当AD=PD时,则AH=PH. ∴2=x﹣2,解得x=4. 情况③:当AP=PD时, 则Rt△DPH中,x2=42+(x﹣2)2 , 解得x=5. ∵2<x<8, ∴当x为2
5
、4、5时,△APD是等腰三角形. (2)∵∠DPE=∠DHP=90°, ∴∠DPH+∠EPB=∠DPH+∠HDP=90°. ∴∠HDP=∠EPB. 又∵∠DHP=∠B=90°, ∴△DPH∽△PEB. ∴
????
????
=
????
????
, ∴
4
???2
=
8???
??
. 整理得:y=
1
4
(x﹣2)(8﹣x)=﹣
1
4
x2+
5
2
x﹣4; (3)存在. 设BC=a,则由(2)得△DPH∽△PEB, ∴
??
8???
=
???2
??
, ∴y=
8???
???2
??
, 当y=a时, (8﹣x)(x﹣2)=a2 x2﹣10x+(16+a2)=0, ∴△=100﹣4(16+a2), ∵△≥0, ∴100﹣64﹣4a2≥0, 4a2≤36, 又∵a>0, ∴a≤3, ∴0<a≤3, ∴满足0<BC≤3时,存在点P,使得PQ经过C.
同课章节目录
- 第1章 一元二次方程
- 1.1 一元二次方程
- 1.2 一元二次方程的解法
- 1.3 一元二次方程的根与系数的关系
- 1.4 用一元二次方程解决问题
- 数学活动 矩形绿地中的花圃设计
- 第2章 对称图形——圆
- 2.1 圆
- 2.2 圆的对称性
- 2.3 确定圆的条件
- 2.4 圆周角
- 2.5 直线与圆的位置关系
- 2.6 正多边形与圆
- 2.7 弧长及扇形的面积
- 2.8 圆锥的侧面积
- 数学活动 图形的密铺
- 第3章 数据的集中趋势和离散程度
- 3.1 平均数
- 3.2 中位数与众数
- 3.3 用计算器求平均数
- 3.4 方差
- 3.5 用计算器求方差
- 数学活动 估测时间
- 第4章 等可能条件下的概率
- 4.1 等可能性
- 4.2 等可能条件下的概率(一)
- 4.3 等可能条件下的概率(二)
- 数学活动 调查“小概率事件”
