2017-2018学年江苏省宿迁市高一(上)期末数学试卷(解析版)
文档属性
| 名称 | 2017-2018学年江苏省宿迁市高一(上)期末数学试卷(解析版) |  | |
| 格式 | zip | ||
| 文件大小 | 113.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-01-13 23:35:28 | ||
图片预览




文档简介
2017-2018学年江苏省宿迁市高一(上)期末数学试卷
一、填空题(本大题共14小题,共60.0分)
已知集合A={1,2},B={-1,2},则A∪B=______.
函数f(x)=lg(x-2)+
3???
的定义域为______.
计算sin(-330°)的值为______.
已知幂函数f(x)=xa的图象经过点(8,2),则f(27)的值为______.
不等式3x-2>1的解集为______.
若将函数f(x)=sin(2x-
??
3
)的图象向左平移φ(φ>0)个单位长度,得到函数g(x)=sin2x的图象,则φ的最小值为______.
计算(
16
81
)
1
4
+log82的值为______.
已知函数y=sin(2x-
??
3
),x∈[0,
??
2
],则它的单调递增区间为______.
若sin(???
??
6
)=
1
3
,其中??<??<
7
6
??,则sin(
2??
3
???)的值为______.
已知向量
??
=(1,-2),
??
=(-1,1),若(
??
?
??
)⊥(
??
+??
??
),则实数k的值为______.
若点P(1,2)在角α终边上,则
????????
????
??
2
???????????????????
的值为______.
已知函数f(x)=
???+3,??>2
|????
??
2
??|,0,若函数g(x)=f(x)-m(m∈R)有三个不同的零点x1,x2,x3,且x1<x2<x3,则(x1x2+1)m-x3的取值范围是______.
已知函数f(x)是定义在R上的奇函数,且f(-1)=0,若对任意的x1,x2∈(-∞,0),当x1≠x2时,都有
??
1
???(
??
1
)?
??
2
???(
??
2
)
??
1
?
??
2
<0成立,则不等式f(x)<0的解集为______.
已知函数f(x)=-x2+ax+1,h(x)=2x,若不等式f(x)>h(x)恰有两个整数解,则实数a的取值范围是______.
二、解答题(本大题共6小题,共90.0分)
设全集U=R,集合A={x|1≤x≤4},B={x|m≤x≤m+1},m∈R. (1)当m=3时,求A∩?UB; (2)若B?A,求实数m的取值范围.
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<π),它的部分图象如图所示. (1)求函数f(x)的解析式; (2)当x∈[?
??
12
,
5??
12
]时,求函数f(x)的值域.
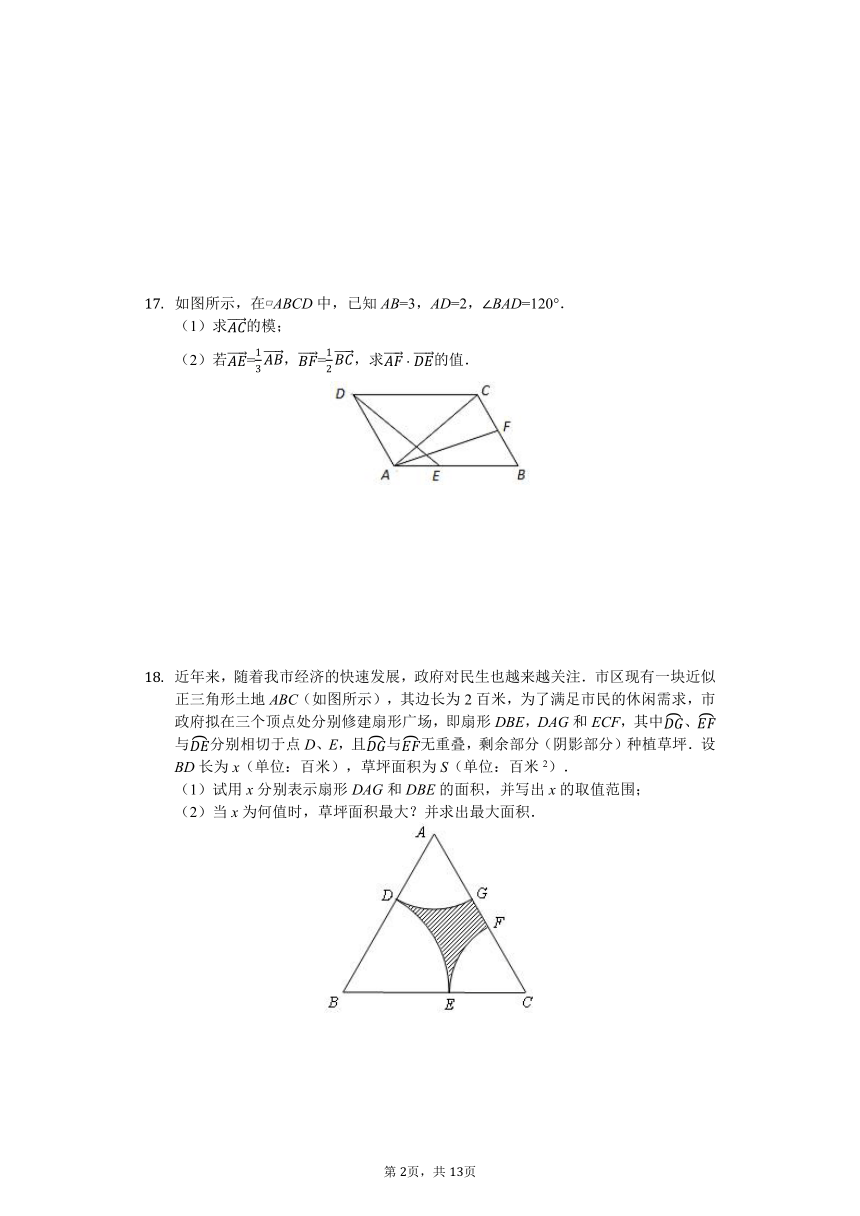
如图所示,在?ABCD中,已知AB=3,AD=2,∠BAD=120°. (1)求
????
的模; (2)若
????
=
1
3
????
,
????
=
1
2
????
,求
????
?
????
的值.
近年来,随着我市经济的快速发展,政府对民生也越来越关注.市区现有一块近似正三角形土地ABC(如图所示),其边长为2百米,为了满足市民的休闲需求,市政府拟在三个顶点处分别修建扇形广场,即扇形DBE,DAG和ECF,其中
????
、
????
与
????
分别相切于点D、E,且
????
与
????
无重叠,剩余部分(阴影部分)种植草坪.设BD长为x(单位:百米),草坪面积为S(单位:百米2). (1)试用x分别表示扇形DAG和DBE的面积,并写出x的取值范围; (2)当x为何值时,草坪面积最大?并求出最大面积.
已知函数f(x)=
|?????|
??
(a>0),且满足f(
1
2
)=1. (1)判断函数f(x)在(1,+∞)上的单调性,并用定义证明; (2)设函数g(x)=
??(??)
??
,求g(x)在区间[
1
2
,4]上的最大值; (3)若存在实数m,使得关于x的方程2(x-a)2-x|x-a|+2mx2=0恰有4个不同的正根,求实数m的取值范围.
已知函数f(x)=log4(a?2x?
4
3
??)(a≠0,a∈R),g(x)=log4(4x+1). (1)设h(x)=g(x)-kx(k∈R),若h(x)是偶函数,求实数k的值; (2)设F(x)=(log2x)-g(log4x),求函数F(x)在区间[2,3]上的值域; (3)若不等式f(x)<g(x)恒成立,求实数a的取值范围.
答案和解析
1.【答案】{-1,1,2} 【解析】
解:A∪B={1,2,-1}. 故答案为:{1,2,-1}. 进行并集的运算即可. 考查列举法表示集合的概念,并集的概念及运算.
2.【答案】(2,3] 【解析】
解:由,解得2<x≤3. ∴函数f(x)=lg(x-2)+的定义域为(2,3]. 故答案为:(2,3]. 由对数式的真数大于0,根式内部的代数式大于等于0联立不等式组求解. 本题考查函数的定义域及其求法,是基础题.
3.【答案】
1
2
【解析】
解:sin(-330°) =sin(-360°+30°) =sin30° =. 故答案为: 把所求式子中的角-330°变为-360°+30°后,利用诱导公式及特殊角的三角函数值即可求出值. 此题考查了运用诱导公式化简求值,灵活变换所求式子的角度,熟练掌握诱导公式是解本题的关键.
4.【答案】3 【解析】
解:幂函数f(x)=xa的图象经过点(8,2), 则8α=2, ∴α=, ∴f(x)=, ∴f(27)==3. 故答案为:3. 根据题意求出α的值,写出函数解析式,再计算f(27)的值. 本题考查了幂函数的定义与应用问题,是基础题.
5.【答案】(2,+∞) 【解析】
解:根据指数函数的单调性知, 不等式3x-2>1可化为x-2>0, 解得x>2, ∴不等式的解集为(2,+∞). 故答案为:(2,+∞). 根据指数函数的单调性,把不等式化为x-2>0,求解集即可. 本题考查了指数函数的图象与性质的应用问题,是基础题.
6.【答案】
??
6
【解析】
解:将函数f(x)=sin(2x-)=sin2(x-)的图象向左平移φ(φ>0)个单位长度, 得到函数g(x)=sin2x的图象, 则φ的最小值为, 故答案为:. 利用函数y=Asin(ωx+φ)的图象变换规律,得出结论. 本题主要考查函数y=Asin(ωx+φ)的图象变换规律,属于基础题.
7.【答案】1 【解析】
解:=. 故答案为:1. 进行指数、对数的运算即可. 考查指数和对数的运算,以及对数的换底公式.
8.【答案】[0,
5??
12
] 【解析】
解:令-,解得, 令,则, 因此,函数的单调递增区间为. 故答案为:. 先求出函数在R上的单调递增区间,然后与定义域取交集,即可求出答案. 本题考查三角函数的单调性,考查推理能力与计算能力,属于中等题.
9.【答案】-
2
2
3
【解析】
解:∵sin(α-)=,其中,∴α-∈(,π),cos(α-)=-=-, 则sin()=sin(+α)=(cos-α)=-, 故答案为:-. 由题意利用同角三角函数的基本关系求得cos(α-)的值,再利用诱导公式求得sin()=sin(+α)=(cos-α)的值. 本题主要考查同角三角函数的基本关系,诱导公式,属于基础题.
10.【答案】
8
5
【解析】
解:向量=(1,-2),=(-1,1), 若()⊥(), 则(-)?(+k)=+(k-1)?-k=0, ∴(1+4)+(k-1)×(-1-2)-k×(1+1)=0, 解得k=. 故答案为:. 根据两向量垂直时数量积为0,列出方程求出k的值. 本题考查了平面向量的坐标运算与数量积运算问题,是基础题.
11.【答案】5 【解析】
解:点P(1,2)在角α终边上,∴tanα==2,sinα==,cosα==, 则==5, 故答案为:5. 由题意利用任意角的三角函数的定义求得 tanα、sinα、cosα 的值,可得要求式子的值. 本题主要考查任意角的三角函数的定义,属于基础题.
12.【答案】(-2,0) 【解析】
解:函数g(x)=f(x)-m(m∈R)有三个不同的零点, 即为g(x)=0,即f(x)=m有三个交点, 由-log2x1=log2x2=3-x3=m,0<m<1, 即有x1x2=1,x3=3-m, 则(x1x2+1)m-x3=2m-3+m, 由h(m)=2m-3+m在(0,1)递增, 可得h(m)的值域为(-2,0). 故答案为:(-2,0). 由题意可得g(x)=0,即f(x)=m有三个交点,可得x1x2=1,x3=3-m,0<m<1,则(x1x2+1)m-x3=2m-3+m,由h(m)=2m-3+m的单调性,即可得到所求范围. 本题考查函数的零点问题,注意运用数形结合思想和构造函数法,考查化简运算能力,属于中档题.
13.【答案】(-∞,-1)∪(0,1) 【解析】
解:根据题意,设g(x)=xf(x), 若函数f(x)是定义在R上的奇函数,即f(-x)=-f(x), 则g(-x)=(-x)f(-x)=xf(x)=g(x),则g(x)为R上的偶函数, 若f(-1)=0,则g(-1)=g(1)=0, 又由对任意的x1,x2∈(-∞,0),当x1≠x2时,都有<0成立,则g(x)在(-∞,0)上为减函数, 则在(-∞,-1)上,g(x)=xf(x)>0,在(-1,0)上,g(x)=xf(x)<0, 又由x∈(-∞,0),则在(-∞,-1)上,f(x)<0,在(-1,0),f(x)>0, 又由f(x)为奇函数,在在(0,1),f(x)<0, 综合可得:f(x)的解集为(-∞,-1)∪(0,1); 故答案为:(-∞,-1)∪(0,1). 根据题意,设g(x)=xf(x),分析可得g(x)为偶函数且在(-∞,0)上为减函数,据此可得在(-∞,-1)上,g(x)=xf(x)>0,在(-1,0)上,g(x)=xf(x)<0,结合x的范围可得在(-∞,-1)上,f(x)<0,在(-1,0),f(x)>0,结合函数f(x)的奇偶性,分析可得答案. 本题考查函数奇偶性与单调性的综合应用,注意构造新函数g(x)=xf(x),属于基础题.
14.【答案】[-
65
24
,-
13
8
)∪(
7
2
,
16
3
] 【解析】
解:由函数f(x)=-x2+ax+1,h(x)=2x可得f(x),g(x)的图象均过(0,1), 且f(x)的对称轴为x=,当a>0时,由题意可得f(x)>h(x)恰有1,2两个整数解, 可得f(2)>h(2),f(3)≤h(3), 即有-3+2a>4,-8+3a≤8, 解得<a≤; 当当a<0时,由题意可得f(x)>h(x)恰有-1,-2两个整数解, 可得f(-2)>h(-2),f(-3)≤h(-3), 即有-3-2a>,-8-3a≤, 解得-≤a<-, 综上可得a的范围是[-,-)∪(,]. 故答案为:[-,-)∪(,]. 由题意可得f(x),g(x)的图象均过(0,1),分别讨论a>0,a<0时,f(x)>h(x)的整数解情况,解不等式即可得到所求范围. 本题考查函数方程的转化思想,考查分类讨论思想方法,以及化简整理的运算能力,属于中档题.
15.【答案】解:(1)当m=3时,B={x|3≤x≤4},…(3分) ∴CUB=(-∞,3)∪(4,+∞),…(6分) 故A∩?UB=[1,3).…(8分) (2)∵B?A,∴
??+1≤4
??≥1
,…(12分) 解得1≤m≤3.…(14分) 【解析】
(1)当m=3时,B={x|3≤x≤4},由此能求出A∩?UB. (2)由B?A,列出不等式组,能求出实数m的取值范围. 本题考查交集、补集、不等式的取值范围的求法,考查补集、交集、子集的定义等基础知识,考查运算求解能力,考查函数与方程思想,是基础题.
16.【答案】解:(1)依题意,A=2,T=4(
??
3
-
??
12
)=π=
2??
??
,ω=2, 故f(x)=2sin(2x+φ) 将点(
??
3
,2)的坐标代入函数的解析式可得sin(
2??
3
+φ)=1 则φ=2kπ-
??
6
(k∈Z),又|φ|<π,故φ=-
??
6
, 故函数解析式为f(x)=2sin(2x-
??
6
) (2)当x∈[-
??
12
,
5??
12
]时,-
??
3
≤2x-
??
6
≤
2??
3
, 则-
3
2
≤sin(2x-
??
6
)≤1,-
3
≤2sin(2x-
??
6
)≤2, 所以函数f(x)的值域为[-
3
,2] 【解析】
(1)由图观察得A,T,利用T求得ω,代最高点(,2)求φ; (2)利用正弦函数的图象求值域. 本题考查了由y=Asin(ωx+φ)的部分图象确定解析式,属中档题.
17.【答案】解:(1)在?ABCD中,已知AB=3,AD=2,∠BAD=120°. |
????
|=|
????
+
????
|=
(
????
+
????
)
2
=
|
????
|
2
+2|
????
||
????
|??????∠??????+|
????
|
2
, =
9+2?3?2?(?
1
2
)+4
, =
7
. (2)由图形得
????
=
????
+
1
2
????
,
????
=
1
3
????
?
????
, 所以:
????
?
????
=(
????
+
1
2
????
)?(
1
3
????
?
????
), =
1
3
|
????
|
2
?
5
6
|
????
||
????
|??????∠???????
1
2
|
????
|
2
, =
1
3
?9?
5
6
?3?2?(?
1
2
)?
1
2
?4, =
7
2
. 【解析】
(1)直接利用向量的线性运算和余弦定理求出结果. (2)利用向量的线性运算和数量积运算求出结果. 本题考查的知识要点:余弦定理的应用,向量的线性运算的应用,向量的模的运算的应用,主要考查学生的运算能力和转化能力,属于基础题型.
18.【答案】解:(1)如图,BD=x,则BE=x,AD=AG=EC=FC=2-x, 在扇形DBE中,弧DE长=
??
3
x, 所以S扇形BDE=
1
2
×
??
3
x2=
??
6
x2, 同理,S扇形ADG=
1
2
×
??
3
(2-x)2=
??
6
(2-x)2, 因为弧DG与弧EF无重叠, 所以CF+AG≤AC,即2-x+2-x≤2,则x≥1, 又三个扇形都在三角形内部,则x≤
3
, 所以x∈[1,
3
]; (2)因为S△ABC=
3
, 所以S阴影=S△ABC-S扇形BDE-S扇形ADG-S扇形CEF=
3
-
??
6
[x2+2(2-x)2], =
3
-
??
6
[3(x-
4
3
)2+
8
3
], 所以当x=
4
3
时,S阴影取得最大值为
3
-
4??
9
, 答:当BD长为
4
3
百米时,草坪面积最大,最大值为(
3
-
4??
9
)百米2. 【解析】
(1)根据扇形的面积公式可得结果,根据条件可得以CF+AG≤AC,且BD长的小于高,解得x的取值范围, (2)列出草坪面积的函数关系式,根据二次函数的性质即可求出. 本题考查了函数在实际生活中的应用,考查了数学建模的思想,属于中档题.
19.【答案】解:(1)由f(
1
2
)=
|
1
2
???|
1
2
=1,得a=1或0. 因为a>0,所以a=1,所以f(x)=
|???1|
??
. 当x>1时,f(x)=
???1
??
=1-
1
??
为增函数, 任取x1,x2∈(1,+∞),且x1<x2, 则f(x1)-f(x2)=1-
1
??
1
-1+
1
??
2
=
??
1
?
??
2
??
1
??
2
, 因为1<x1<x2,则x1-x2<0,x1x2>0,f(x1)-f(x2)<0, 所以f(x)在(1,+∞)上为增函数; (2)g(x)=
??(??)
??
=
|???1|
??
2
=
???1
??
2
,1≤??≤4
1???
??
2
,
1
2
≤??<1
, 当1≤x≤4时,g(x)=
???1
??
2
=
1
??
-
1
??
2
=-(
1
??
-
1
2
)2+
1
4
, 因为
1
4
≤
1
??
≤1,所以当
1
??
=
1
2
时,g(x)max=
1
4
; 当
1
2
≤x<1时,g(x)=
1???
??
2
=(
1
??
-
1
2
)2-
1
4
, 因为
1
2
≤x<1时,所以1<
1
??
≤2,所以当
1
??
=2时,g(x)max=2; 综上,当x=
1
2
时,g(x)max=2; (3)由(1)可知,f(x)在(1,+∞)上为增函数,当x>1时,f(x)=1-
1
??
∈(0,1). 同理可得f(x)在(0,1)上为减函数,当0<x<1时,f(x)=
1
??
-1∈(0,+∞). 方程2(x-1)2-x|x-1|+2mx2=0可化为2?
|???1
|
2
??
2
-
|???1|
??
+2m=0, 即2f2(x)-f(x)+2m=0, 设t=f(x),方程可化为2t2-t+2m=0, 要使原方程有4个不同的正根, 则方程2t2-t+2m=0在(0,1)有两个不等的根t1,t2, 则有
1?16??>0
2??>0
2×
1
2
?1+2??>0
,解得0<m<
1
16
, 所以实数m的取值范围为(0,
1
16
). 【解析】
(1)由f()=1,解方程可得a,再由单调性的定义,即可证得f(x)在(1,+∞)上为增函数; (2)运用分段函数写出g(x),讨论1≤x≤4,≤x<1,结合二次函数的最值求法,可得所求最大值; (3)由题意可得方程2(x-1)2-x|x-1|+2mx2=0可化为2?-+2m=0,即2f2(x)-f(x)+2m=0, 设t=f(x),方程可化为2t2-t+2m=0,由题意可得方程2t2-t+2m=0在(0,1)有两个不等的根t1,t2,可得m的不等式,解不等式即可得到所求范围. 本题考查函数的解析式的求法,注意运用方程思想,考查函数的最值求法,注意运用分类讨论思想方法,考查存在性问题解法,注意运用换元法和转化思想,讨论二次方程实根分布,考查化简整理的运算能力,属于中档题.
20.【答案】解:(1)因为h(x)=log4(4x+1)-kx是偶函数, 所以log4(4-x+1)+kx=log4(4x+1)-kx, 则2kx=log4
4
??
+1
4
???
+1
=log44x=x恒成立, 所以k=
1
2
; (2)F(x)=f(log2x)-g(log4x)=log4(ax-
4
3
a)-log4(x+1) =log4
??(???
4
3
)
??+1
=log4[a(1-
7
3(??+1)
], 因为x∈[2,3],所以x-
4
3
>0,所以a>0, 则1-
7
3(??+1)
∈[
2
9
,
5
12
],a>0, 则a(1-
7
3(??+1)
)∈[
2
9
a,
5
12
a], 所以F(x)∈[log4
2
9
a,log4
5
12
a]; 即函数F(x)的值域为[log4
2
9
a,log4
5
12
a]; (3)由f(x)<g(x),得log4(a?2x?
4
3
??)<log4(4x+1), 设t=2x,则t2-at+1+
4
3
a>0,设m(t)=t2-at+1+
4
3
a, 若a>0则t>
4
3
,由不等式t2-at+1+
4
3
a>0对t>
4
3
恒成立, ①当
??
2
≤
4
3
,即0<a≤
8
3
时,此时m(
4
3
)=
25
9
>0恒成立; ②当
??
2
>
4
3
,即a>
8
3
时,由△=a2-4-
16
3
a<0解得
8
3
<a<6; 所以0<a<6; 若a<0则0<t<
4
3
,则由不等式t2-at+1+
4
3
a>0对0<t<
4
3
恒成立, 因为a<0,所以
??
2
<0,只需m(0)=1+
4
3
a≥0,解得-
3
4
≤a<0; 故实数a的取值范围是[-
3
4
,0)∪(0,6). 【解析】
(1)运用偶函数的定义,化简整理可得k的值; (2)求得F(x)的解析式,运用对数函数的单调性即可得到所求值域; (3)由f(x)<g(x),得log4(a?2x)<log4(4x+1),设t=2x,则t2-at+1+a>0,设m(t)=t2-at+1+a, 讨论a>0,a<0,结合对称轴和区间的关系,解不等式即可得到所求范围. 本题考查函数的奇偶性的定义,考查函数的值域求法,注意运用对数函数的单调性,考查不等式恒成立问题解法,注意运用换元法和分类讨论思想方法,考查化简整理的运算能力,属于中档题.
同课章节目录
