人教版八年级下《第二十章数据的分析》单元检测试题(含答案)
文档属性
| 名称 | 人教版八年级下《第二十章数据的分析》单元检测试题(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 270.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-01-16 06:18:09 | ||
图片预览



文档简介
第二十章 检测试题
一、选择题(每小题4分,共48分)
1.一组数据:5,7,10,5,7,5,6,这组数据的众数和中位数分别( )
(A)10和7 (B)5和7 (C)6和7 (D)5和6
2.某中学规定学生的学期体育成绩满分为100分,其中课外体育占20%,期中考试成绩占30%,期末考试成绩占50%.张明的三项成绩(百分制)依次为95,90,88,则张明这学期的体育成绩为( )
(A)89 (B)90 (C)92 (D)93
3.要判断一个学生的数学考试成绩是否稳定,那么需要知道他最近连续几次数学考试成绩的( )
(A)平均数 (B)中位数 (C)众数 (D)方差
4.近年来,我国持续大面积的雾霾天气让环保和健康问题成为焦点,为进一步普及环保和健康知识,某校举行了“关注环境保护”的知识竞赛,某班学生的成绩统计如下:
成绩(分)
60
70
80
90
100
人数
4
8
12
11
5
则该班学生成绩的众数和中位数分别是( )
(A)70分,80分 (B)80分,80分 (C)90分,80分 (D)80分,90分
5.一组数据2,3,2,3,5的方差是( )
(A)6 (B)3 (C)1.2 (D)2
6.八年级一班和二班每班选8名同学进行投篮比赛,每名同学投篮10次,对每名同学投中的次数进行统计,甲说:“一班同学投中次数为6个的最多.”乙说:“二班同学投中次数最多与最少的相差6个.”上面两名同学的议论能反映出的统计量是( )
(A)平均数和众数 (B)众数和极差(C)众数和方差(D)中位数和极差
7.某校八年级甲、乙两班学生在一学期里的多次检测中,其数学成绩的平均分相等,但两班成绩的方差不等,那么能够正确评价他们的数学学习情况的是( )
(A)学习水平一样
(B)成绩虽然一样,但方差大的班里学生学习潜力大
(C)虽然平均成绩一样,但方差小的班学习成绩稳定
(D)方差较小的班学习成绩不稳定,忽高忽低
8.7名同学参加数学竞赛初赛,他们的得分互不相同,按从高分录到低分的原则,取前4名同学参加复赛,现在小明同学已经知道自己的分数,如果他想知道自己能否进入复赛,那么还需知道所有参赛学生成绩的( )
(A)平均数 (B)中位数 (C)众数 (D)方差
9.某市某一周的PM2.5(大气中直径小于等于2.5微米的颗粒物,也称可入肺颗粒物)指数如表,则该周PM2.5指数的众数和中位数分别是( )
PM2.5指数
150
155
160
165
天数
3
2
1
1
(A)150,150 (B)150,155 (C)155,150 (D)150,152.5
10.在一次统计调查中,小明得到以下一组数据2,4,x,2,4,7的众数是2,则这组数据的平均数、中位数分别为( )
(A)3.5,3 (B)3,4 (C)3,3.5 (D)4,3
11.已知:一组数据x1,x2,x3,x4,x5的平均数是2,方差是,那么另一组数据3x1-2,3x2-2,3x3-2,3x4-2,3x5-2的平均数和方差分别是( )
(A)2, (B)2,1 (C)4, (D)4,3
12.
某射击小组有20人,教练根据他们某次射击的数据绘制成如图所示的统计图,则这组数据的众数和中位数分别是( )
(A)7,7 (B)8,7.5 (C)7,7.5 (D)8,6.5
二、填空题(每小题4分,共20分)
13.某班中考数学成绩如下:7人得100分,14人得90分,17人得80分,8人得70分,3人得60分,1人得50分,那么中考全班数学成绩的平均分为 ,中位数为 ,众数为 .?
14.某校规定学生的数学学期综合成绩是由平时、期中和期末三项成绩按3∶3∶4的比例计算所得.若某同学本学期数学的平时、期中和期末成绩分别是90分、90分和85分,则他本学期数学学期综合成绩是 分.?
15.张老师对同学们的打字能力进行测试,他将全班同学分成五组.经统计,这五个小组平均每分钟打字个数如下:100,80,x,90,90,已知这组数据的众数与平均数相等,那么这组数据的中位数是 .?
16.某校五个绿化小组一天的植树棵数如下:10,10,12,x,8.已知这组数据的平均数是10,那么这组数据的方差是 .?
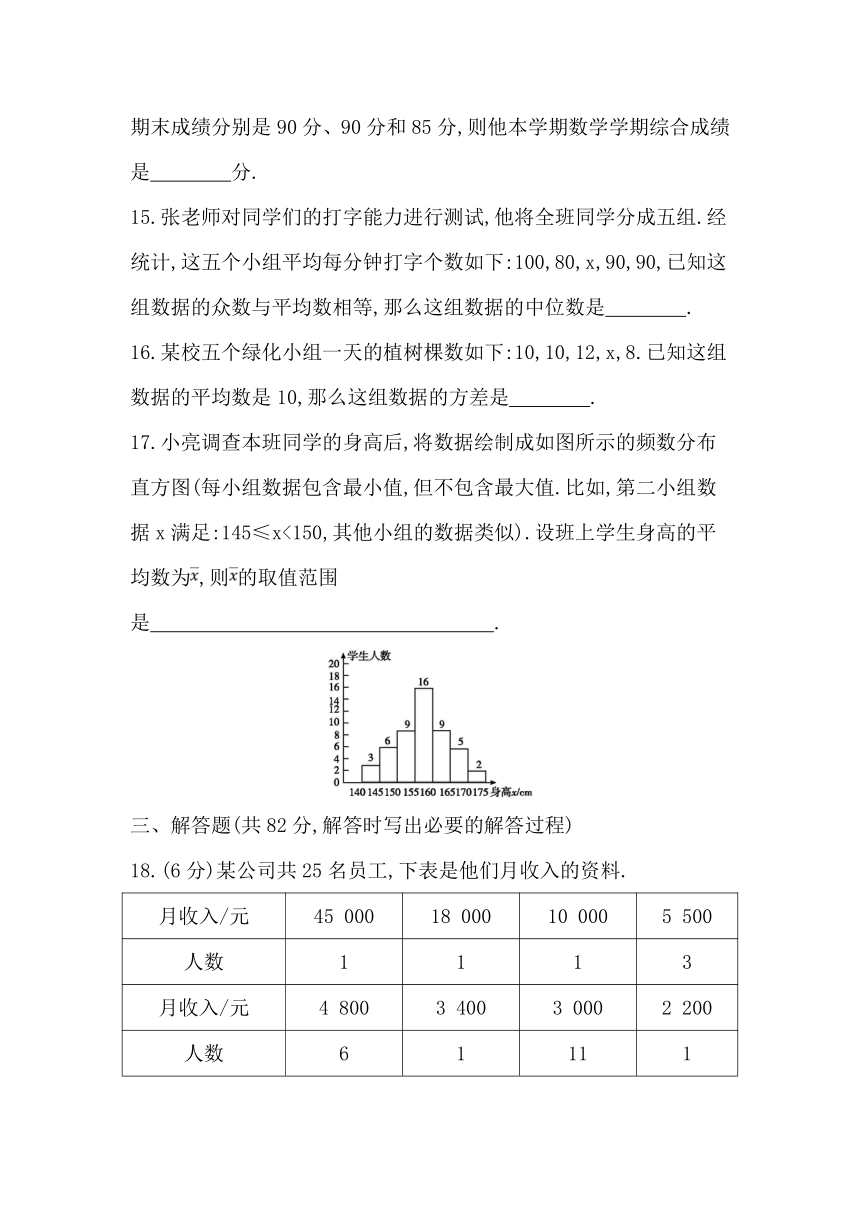
17.小亮调查本班同学的身高后,将数据绘制成如图所示的频数分布直方图(每小组数据包含最小值,但不包含最大值.比如,第二小组数据x满足:145≤x<150,其他小组的数据类似).设班上学生身高的平均数为,则的取值范围是 .?
三、解答题(共82分,解答时写出必要的解答过程)
18.(6分)某公司共25名员工,下表是他们月收入的资料.
月收入/元
45 000
18 000
10 000
5 500
人数
1
1
1
3
月收入/元
4 800
3 400
3 000
2 200
人数
6
1
11
1
(1)该公司员工月收入的中位数是 元,众数是 元;?
(2)根据上表,可以算得该公司员工月收入的平均数为6 276元.你认为用平均数、中位数和众数中的哪一个反映该公司全体员工月收入水平较为合适?说明理由.
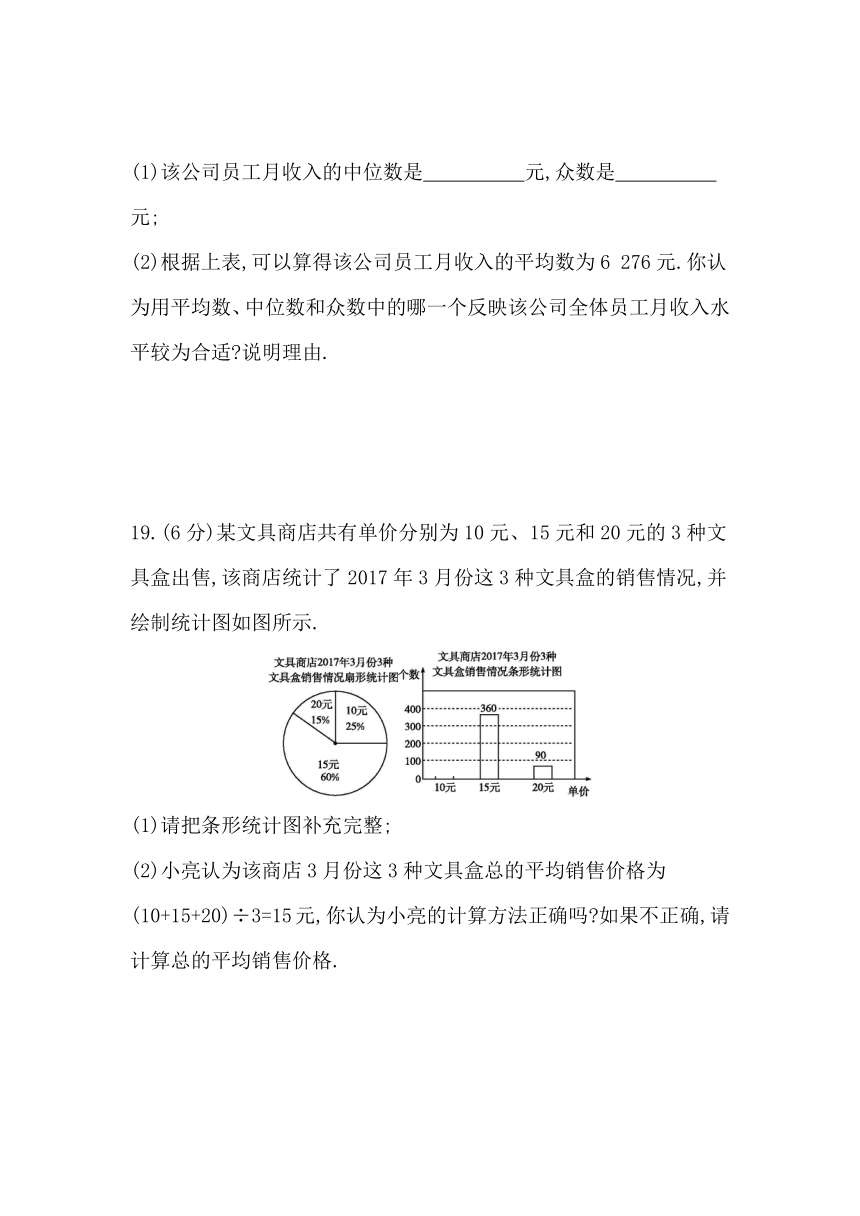
19.(6分)某文具商店共有单价分别为10元、15元和20元的3种文具盒出售,该商店统计了2017年3月份这3种文具盒的销售情况,并绘制统计图如图所示.
(1)请把条形统计图补充完整;
(2)小亮认为该商店3月份这3种文具盒总的平均销售价格为(10+15+20)÷3=15元,你认为小亮的计算方法正确吗?如果不正确,请计算总的平均销售价格.
20.(8分)为了宣传节约用水,小明随机调查了某小区家庭5月份的用水情况,并将收集的数据整理成如图所示的统计图.
(1)小明一共调查了多少户家庭?
(2)求所调查家庭5月份用水量的平均数;
(3)若该小区有400户居民,请你估计这个小区5月份的用水量.
21.(8分)甲、乙两台机床同时生产同一种零件,在10天中两台机床每天生产的次品数如下:
甲:0,1,0,2,2,0,3,1,2,4;
乙:2,3,1,1,0,2,1,1,0,1.
(1)分别计算两组数据的平均数和方差;
(2)从结果看,在10天中哪台机床出现次品的波动较小?
(3)由此推测哪台机床的性能较好
22.(8分)(2018云南)某同学参加了学校举行的“五好小公民·红旗飘飘”演讲比赛,7位评委给该同学的打分(单位:分)情况如下表:
评委
评委1
评委2
评委3
评委4
评委5
评委6
评委7
打分
6
8
7
8
5
7
8
(1)直接写出该同学所得分数的众数与中位数;
(2)计算该同学所得分数的平均数.
23.
(10分)某学校举行演讲比赛,选出了10名同学担任评委,并事先拟定从如下4个方案中选择合理的
方案来确定每个演讲者的最后得分(满分为10分):
方案①:所有评委所给分的平均数.
方案②:在所有评委所给分中,去掉一个最高分和一个最低分,然后再计算其余给分的平均数.
方案③:所有评委所给分的中位数.
方案④:所有评委所给分的众数.
为了探究上述方案的合理性,先对某个同学的演讲成绩进行了统计实验.如图是这个同学的得分统计图.
(1)分别按上述4个方案计算这个同学演讲的最后得分;
(2)根据(1)中的结果,请用统计的知识说明哪些方案不适合作为这个同学演讲的最后得分.
24.(10分)(2018包头)某公司招聘职员两名,对甲、乙、丙、丁四名候选人进行了笔试和面试,各项成绩满分均为100分,然后再按笔试占60%、面试占40%计算候选人的综合成绩(满分为100分).
他们的各项成绩如下表所示:
候选人
笔试成绩/分
面试成绩/分
甲
90
88
乙
84
92
丙
x
90
丁
88
86
(1)直接写出这四名候选人面试成绩的中位数;
(2)现得知候选人丙的综合成绩为87.6分,求表中x的值;
(3)求出其余三名候选人的综合成绩,并以综合成绩排序确定所要招聘的前两名的人选.
25.(12分)某中学七、八年级各选派10名选手参加学校举办的知识竞赛,计分采用10分制,选手得分均为整数,成绩达到6分或6分以上为合格,达到9分或10分为优秀.这次竞赛后,七、八年级两支代表队选手成绩分布的条形统计图和成绩统计分析表如下所示,其中七年级代表队得6分、10分的选手人数为a,b.
队别
平均分
中位数
方差
合格率
优秀率
七年级
6.7
m
3.41
90%
n
八年级
7.1
7.5
1.69
80%
10%
(1)请依据图表中的数据,求a,b的值;
(2)直接写出表中的m,n的值;
(3)有人说七年级队的合格率、优秀率均高于八年级,所以七年级队成绩比八年级队好,但也有人说八年级队成绩比七年级队好.请你给出两条支持八年级队成绩好的理由.
26.(14分)某高中学校为使高一新生入校后及时穿上合身的校服,现提前对某校九年级(3)班学生即将所穿校服型号情况进行了摸底调查,并根据调查结果绘制了如图两个不完整的统计图(校服型号以身高作为标准,共分为6种型号).
根据以上信息,解答下列问题:
(1)该班共有多少名学生?其中穿175型校服的学生有多少人?
(2)在条形统计图中,请把空缺的部分补充完整;
(3)在扇形统计图中,请计算185型校服所对应扇形圆心角的大小;
(4)求该班学生所穿校服型号的众数和中位数.
第二十章 检测试题参考答案
1.D 2.B 3.D 4.B 5.C 6.B 7.C 8.B 9.B 10.A 11.D
12.C
13.82.2 80 80 14.88
15.90
16.1.6 17.154.5≤<159.5
18.解:(1)共有25名员工,中位数是第13个数,
则中位数是3 400元;
3 000出现了11次,出现的次数最多,则众数是3 000元.
(2)用中位数或众数来描述更为恰当.理由:
平均数受极端值45 000元的影响,只有3个人的工资达到了6 276元,不恰当.
19.解:(1)由题意知,单价为10元的文具盒的销售数量为90÷15%×25%=150(个),
补全条形统计图,如图所示.
(2)小亮的计算方法不正确.
法一 总的平均销售价格为20×15%+10×25%+15×60%=14.5(元).
法二 总的平均销售价格为(10×150+15×360+20×90)÷(150+360+90)=8 700÷600=14.5(元).
20.解:(1)1+1+3+6+4+2+2+1=20(户).
答:小明一共调查了20户家庭.
(2)所调查家庭5月份用水量的平均数为(1×1+2×1+3×3+
4×6+5×4+6×2+7×2+8×1)÷20=4.5(吨),
答:所调查家庭5月份用水量的平均数为 4.5 吨.
(3)400×4.5=1 800(吨).
答:估计这个小区5月份的用水量为1 800吨.
21.解:(1)甲的平均数是
=×(0+1+0+2+2+0+3+1+2+4)=1.5;
乙的平均数是
=×(2+3+1+1+0+2+1+1+0+1)=1.2.
甲的方差是=[(0-1.5)2+(1-1.5)2+(0-1.5)2+…+(4-1.5)2]=1.65;
乙的方差是=[(2-1.2)2+(3-1.2)2+(1-1.2)2+…+(1-1.2)2]=0.76.
(2)因为=1.65,=0.76,所以>,
所以乙机床出现次品的波动较小.
(3)乙的平均数比甲的平均数小,且>,
所以乙机床的性能较好.
22.解:(1)众数为8分,中位数为7分.
(2)=×(6+8+7+8+5+7+8)=7(分).
答:该同学所得分数的平均数为7分.
23.解:(1)方案①最后得分:×(3.2+7.0+7.8+3×8+3×8.4+9.8)=7.7;
方案②最后得分:(7.0+7.8+3×8+3×8.4)=8;
方案③最后得分:中位数是8;
方案④最后得分:众数是8或8.4.
(2)因为方案①中的平均数受极端数值的影响,不适合作为这个同学演讲的最后得分,方案④中的众数有两个,众数失去了实际意义,不适合作为最后得分的方案.所以方案①和方案④不适合作为这个同学演讲的最后得分.
24.解:(1)这四名候选人面试成绩的中位数为=89(分).
(2)由题意得,x×60%+90×40%=87.6,解得,x=86.
答:表中x的值为86.
(3)甲候选人的综合成绩为90×60%+88×40%=89.2(分),
乙候选人的综合成绩为84×60%+92×40%=87.2(分),
丁候选人的综合成绩为88×60%+86×40%=87.2(分),
∴以综合成绩排序确定所要招聘的前两名的人选是甲和丙.
25.解:(1)由题意,得
解得
(2)m=6,n=20%.
(3)①八年级队平均分高于七年级队;
②八年级队的成绩比七年级队的稳定;
③八年级队的成绩集中在中上游.
答案不唯一,以上三条中任选两条即可.
26.解:(1)该班的学生总人数为15÷30%=50(名),
穿175型校服的学生人数为50×20%=10(名).
答:该班共有50名学生,其中穿175型校服的学生有10名.
(2)穿185型校服的学生人数为50-3-15-15-10-5=50-48=2(名),
补全条形统计图,如图所示.
(3)185型校服所对应的扇形圆心角为×360°=14.4°.
答:185型校服所对应的圆心角的大小为14.4°.
(4)165型和170型出现的次数最多,都是15次,
所以众数是165和170.共有50个数据,第25,26个数据都是170,所以中位数是170.
答:该班学生所穿校服型号的众数是165和170,中位数是170.
一、选择题(每小题4分,共48分)
1.一组数据:5,7,10,5,7,5,6,这组数据的众数和中位数分别( )
(A)10和7 (B)5和7 (C)6和7 (D)5和6
2.某中学规定学生的学期体育成绩满分为100分,其中课外体育占20%,期中考试成绩占30%,期末考试成绩占50%.张明的三项成绩(百分制)依次为95,90,88,则张明这学期的体育成绩为( )
(A)89 (B)90 (C)92 (D)93
3.要判断一个学生的数学考试成绩是否稳定,那么需要知道他最近连续几次数学考试成绩的( )
(A)平均数 (B)中位数 (C)众数 (D)方差
4.近年来,我国持续大面积的雾霾天气让环保和健康问题成为焦点,为进一步普及环保和健康知识,某校举行了“关注环境保护”的知识竞赛,某班学生的成绩统计如下:
成绩(分)
60
70
80
90
100
人数
4
8
12
11
5
则该班学生成绩的众数和中位数分别是( )
(A)70分,80分 (B)80分,80分 (C)90分,80分 (D)80分,90分
5.一组数据2,3,2,3,5的方差是( )
(A)6 (B)3 (C)1.2 (D)2
6.八年级一班和二班每班选8名同学进行投篮比赛,每名同学投篮10次,对每名同学投中的次数进行统计,甲说:“一班同学投中次数为6个的最多.”乙说:“二班同学投中次数最多与最少的相差6个.”上面两名同学的议论能反映出的统计量是( )
(A)平均数和众数 (B)众数和极差(C)众数和方差(D)中位数和极差
7.某校八年级甲、乙两班学生在一学期里的多次检测中,其数学成绩的平均分相等,但两班成绩的方差不等,那么能够正确评价他们的数学学习情况的是( )
(A)学习水平一样
(B)成绩虽然一样,但方差大的班里学生学习潜力大
(C)虽然平均成绩一样,但方差小的班学习成绩稳定
(D)方差较小的班学习成绩不稳定,忽高忽低
8.7名同学参加数学竞赛初赛,他们的得分互不相同,按从高分录到低分的原则,取前4名同学参加复赛,现在小明同学已经知道自己的分数,如果他想知道自己能否进入复赛,那么还需知道所有参赛学生成绩的( )
(A)平均数 (B)中位数 (C)众数 (D)方差
9.某市某一周的PM2.5(大气中直径小于等于2.5微米的颗粒物,也称可入肺颗粒物)指数如表,则该周PM2.5指数的众数和中位数分别是( )
PM2.5指数
150
155
160
165
天数
3
2
1
1
(A)150,150 (B)150,155 (C)155,150 (D)150,152.5
10.在一次统计调查中,小明得到以下一组数据2,4,x,2,4,7的众数是2,则这组数据的平均数、中位数分别为( )
(A)3.5,3 (B)3,4 (C)3,3.5 (D)4,3
11.已知:一组数据x1,x2,x3,x4,x5的平均数是2,方差是,那么另一组数据3x1-2,3x2-2,3x3-2,3x4-2,3x5-2的平均数和方差分别是( )
(A)2, (B)2,1 (C)4, (D)4,3
12.
某射击小组有20人,教练根据他们某次射击的数据绘制成如图所示的统计图,则这组数据的众数和中位数分别是( )
(A)7,7 (B)8,7.5 (C)7,7.5 (D)8,6.5
二、填空题(每小题4分,共20分)
13.某班中考数学成绩如下:7人得100分,14人得90分,17人得80分,8人得70分,3人得60分,1人得50分,那么中考全班数学成绩的平均分为 ,中位数为 ,众数为 .?
14.某校规定学生的数学学期综合成绩是由平时、期中和期末三项成绩按3∶3∶4的比例计算所得.若某同学本学期数学的平时、期中和期末成绩分别是90分、90分和85分,则他本学期数学学期综合成绩是 分.?
15.张老师对同学们的打字能力进行测试,他将全班同学分成五组.经统计,这五个小组平均每分钟打字个数如下:100,80,x,90,90,已知这组数据的众数与平均数相等,那么这组数据的中位数是 .?
16.某校五个绿化小组一天的植树棵数如下:10,10,12,x,8.已知这组数据的平均数是10,那么这组数据的方差是 .?
17.小亮调查本班同学的身高后,将数据绘制成如图所示的频数分布直方图(每小组数据包含最小值,但不包含最大值.比如,第二小组数据x满足:145≤x<150,其他小组的数据类似).设班上学生身高的平均数为,则的取值范围是 .?
三、解答题(共82分,解答时写出必要的解答过程)
18.(6分)某公司共25名员工,下表是他们月收入的资料.
月收入/元
45 000
18 000
10 000
5 500
人数
1
1
1
3
月收入/元
4 800
3 400
3 000
2 200
人数
6
1
11
1
(1)该公司员工月收入的中位数是 元,众数是 元;?
(2)根据上表,可以算得该公司员工月收入的平均数为6 276元.你认为用平均数、中位数和众数中的哪一个反映该公司全体员工月收入水平较为合适?说明理由.
19.(6分)某文具商店共有单价分别为10元、15元和20元的3种文具盒出售,该商店统计了2017年3月份这3种文具盒的销售情况,并绘制统计图如图所示.
(1)请把条形统计图补充完整;
(2)小亮认为该商店3月份这3种文具盒总的平均销售价格为(10+15+20)÷3=15元,你认为小亮的计算方法正确吗?如果不正确,请计算总的平均销售价格.
20.(8分)为了宣传节约用水,小明随机调查了某小区家庭5月份的用水情况,并将收集的数据整理成如图所示的统计图.
(1)小明一共调查了多少户家庭?
(2)求所调查家庭5月份用水量的平均数;
(3)若该小区有400户居民,请你估计这个小区5月份的用水量.
21.(8分)甲、乙两台机床同时生产同一种零件,在10天中两台机床每天生产的次品数如下:
甲:0,1,0,2,2,0,3,1,2,4;
乙:2,3,1,1,0,2,1,1,0,1.
(1)分别计算两组数据的平均数和方差;
(2)从结果看,在10天中哪台机床出现次品的波动较小?
(3)由此推测哪台机床的性能较好
22.(8分)(2018云南)某同学参加了学校举行的“五好小公民·红旗飘飘”演讲比赛,7位评委给该同学的打分(单位:分)情况如下表:
评委
评委1
评委2
评委3
评委4
评委5
评委6
评委7
打分
6
8
7
8
5
7
8
(1)直接写出该同学所得分数的众数与中位数;
(2)计算该同学所得分数的平均数.
23.
(10分)某学校举行演讲比赛,选出了10名同学担任评委,并事先拟定从如下4个方案中选择合理的
方案来确定每个演讲者的最后得分(满分为10分):
方案①:所有评委所给分的平均数.
方案②:在所有评委所给分中,去掉一个最高分和一个最低分,然后再计算其余给分的平均数.
方案③:所有评委所给分的中位数.
方案④:所有评委所给分的众数.
为了探究上述方案的合理性,先对某个同学的演讲成绩进行了统计实验.如图是这个同学的得分统计图.
(1)分别按上述4个方案计算这个同学演讲的最后得分;
(2)根据(1)中的结果,请用统计的知识说明哪些方案不适合作为这个同学演讲的最后得分.
24.(10分)(2018包头)某公司招聘职员两名,对甲、乙、丙、丁四名候选人进行了笔试和面试,各项成绩满分均为100分,然后再按笔试占60%、面试占40%计算候选人的综合成绩(满分为100分).
他们的各项成绩如下表所示:
候选人
笔试成绩/分
面试成绩/分
甲
90
88
乙
84
92
丙
x
90
丁
88
86
(1)直接写出这四名候选人面试成绩的中位数;
(2)现得知候选人丙的综合成绩为87.6分,求表中x的值;
(3)求出其余三名候选人的综合成绩,并以综合成绩排序确定所要招聘的前两名的人选.
25.(12分)某中学七、八年级各选派10名选手参加学校举办的知识竞赛,计分采用10分制,选手得分均为整数,成绩达到6分或6分以上为合格,达到9分或10分为优秀.这次竞赛后,七、八年级两支代表队选手成绩分布的条形统计图和成绩统计分析表如下所示,其中七年级代表队得6分、10分的选手人数为a,b.
队别
平均分
中位数
方差
合格率
优秀率
七年级
6.7
m
3.41
90%
n
八年级
7.1
7.5
1.69
80%
10%
(1)请依据图表中的数据,求a,b的值;
(2)直接写出表中的m,n的值;
(3)有人说七年级队的合格率、优秀率均高于八年级,所以七年级队成绩比八年级队好,但也有人说八年级队成绩比七年级队好.请你给出两条支持八年级队成绩好的理由.
26.(14分)某高中学校为使高一新生入校后及时穿上合身的校服,现提前对某校九年级(3)班学生即将所穿校服型号情况进行了摸底调查,并根据调查结果绘制了如图两个不完整的统计图(校服型号以身高作为标准,共分为6种型号).
根据以上信息,解答下列问题:
(1)该班共有多少名学生?其中穿175型校服的学生有多少人?
(2)在条形统计图中,请把空缺的部分补充完整;
(3)在扇形统计图中,请计算185型校服所对应扇形圆心角的大小;
(4)求该班学生所穿校服型号的众数和中位数.
第二十章 检测试题参考答案
1.D 2.B 3.D 4.B 5.C 6.B 7.C 8.B 9.B 10.A 11.D
12.C
13.82.2 80 80 14.88
15.90
16.1.6 17.154.5≤<159.5
18.解:(1)共有25名员工,中位数是第13个数,
则中位数是3 400元;
3 000出现了11次,出现的次数最多,则众数是3 000元.
(2)用中位数或众数来描述更为恰当.理由:
平均数受极端值45 000元的影响,只有3个人的工资达到了6 276元,不恰当.
19.解:(1)由题意知,单价为10元的文具盒的销售数量为90÷15%×25%=150(个),
补全条形统计图,如图所示.
(2)小亮的计算方法不正确.
法一 总的平均销售价格为20×15%+10×25%+15×60%=14.5(元).
法二 总的平均销售价格为(10×150+15×360+20×90)÷(150+360+90)=8 700÷600=14.5(元).
20.解:(1)1+1+3+6+4+2+2+1=20(户).
答:小明一共调查了20户家庭.
(2)所调查家庭5月份用水量的平均数为(1×1+2×1+3×3+
4×6+5×4+6×2+7×2+8×1)÷20=4.5(吨),
答:所调查家庭5月份用水量的平均数为 4.5 吨.
(3)400×4.5=1 800(吨).
答:估计这个小区5月份的用水量为1 800吨.
21.解:(1)甲的平均数是
=×(0+1+0+2+2+0+3+1+2+4)=1.5;
乙的平均数是
=×(2+3+1+1+0+2+1+1+0+1)=1.2.
甲的方差是=[(0-1.5)2+(1-1.5)2+(0-1.5)2+…+(4-1.5)2]=1.65;
乙的方差是=[(2-1.2)2+(3-1.2)2+(1-1.2)2+…+(1-1.2)2]=0.76.
(2)因为=1.65,=0.76,所以>,
所以乙机床出现次品的波动较小.
(3)乙的平均数比甲的平均数小,且>,
所以乙机床的性能较好.
22.解:(1)众数为8分,中位数为7分.
(2)=×(6+8+7+8+5+7+8)=7(分).
答:该同学所得分数的平均数为7分.
23.解:(1)方案①最后得分:×(3.2+7.0+7.8+3×8+3×8.4+9.8)=7.7;
方案②最后得分:(7.0+7.8+3×8+3×8.4)=8;
方案③最后得分:中位数是8;
方案④最后得分:众数是8或8.4.
(2)因为方案①中的平均数受极端数值的影响,不适合作为这个同学演讲的最后得分,方案④中的众数有两个,众数失去了实际意义,不适合作为最后得分的方案.所以方案①和方案④不适合作为这个同学演讲的最后得分.
24.解:(1)这四名候选人面试成绩的中位数为=89(分).
(2)由题意得,x×60%+90×40%=87.6,解得,x=86.
答:表中x的值为86.
(3)甲候选人的综合成绩为90×60%+88×40%=89.2(分),
乙候选人的综合成绩为84×60%+92×40%=87.2(分),
丁候选人的综合成绩为88×60%+86×40%=87.2(分),
∴以综合成绩排序确定所要招聘的前两名的人选是甲和丙.
25.解:(1)由题意,得
解得
(2)m=6,n=20%.
(3)①八年级队平均分高于七年级队;
②八年级队的成绩比七年级队的稳定;
③八年级队的成绩集中在中上游.
答案不唯一,以上三条中任选两条即可.
26.解:(1)该班的学生总人数为15÷30%=50(名),
穿175型校服的学生人数为50×20%=10(名).
答:该班共有50名学生,其中穿175型校服的学生有10名.
(2)穿185型校服的学生人数为50-3-15-15-10-5=50-48=2(名),
补全条形统计图,如图所示.
(3)185型校服所对应的扇形圆心角为×360°=14.4°.
答:185型校服所对应的圆心角的大小为14.4°.
(4)165型和170型出现的次数最多,都是15次,
所以众数是165和170.共有50个数据,第25,26个数据都是170,所以中位数是170.
答:该班学生所穿校服型号的众数是165和170,中位数是170.
