人教B版数学选修1-2 2.2.2反证法(18张)
文档属性
| 名称 | 人教B版数学选修1-2 2.2.2反证法(18张) |

|
|
| 格式 | zip | ||
| 文件大小 | 225.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-01-17 00:00:00 | ||
图片预览






文档简介
2.2.2 反证法
1.了解反证法是间接证明中最基本和最常用的一种方法.
2.熟练掌握用反证法证题的三个步骤:(1)反设;(2)归谬;(3)结论.
3.认识反证法在数学证明中的重要作用;学会用反证法证题,并能根据题目的类型合理选择证明问题的方法;学会寻找问题中的矛盾,进行正确推理.
反证法
一般地,由证明p?q转向证明????q?r?…?t,
t与假设矛盾,或与某个真命题矛盾,从而判定????q为假,推出q为真的方法,叫做反证法.
知识拓展(1)反证法的实质:证明命题的否定为假,所以命题为真.
(2)应用反证法证明数学命题的一般步骤:
①分清命题的条件和结论;
②作出与命题结论相矛盾的假定;
③由假定出发,应用正确的推理方法,推出矛盾的结果;
④断定产生矛盾结果的原因,在于开始所作的假定不真,于是原结论成立,从而间接地证明命题为真.
(3)反证法的适用情形:
①否定性命题;
②唯一性问题;
③至多至少问题.
(4)用反证法证明命题得出矛盾的方法:
①与假定矛盾;
②与数学公理、定理、公式、定义或已被证明了的结论矛盾;
③与公认的简单事实矛盾.
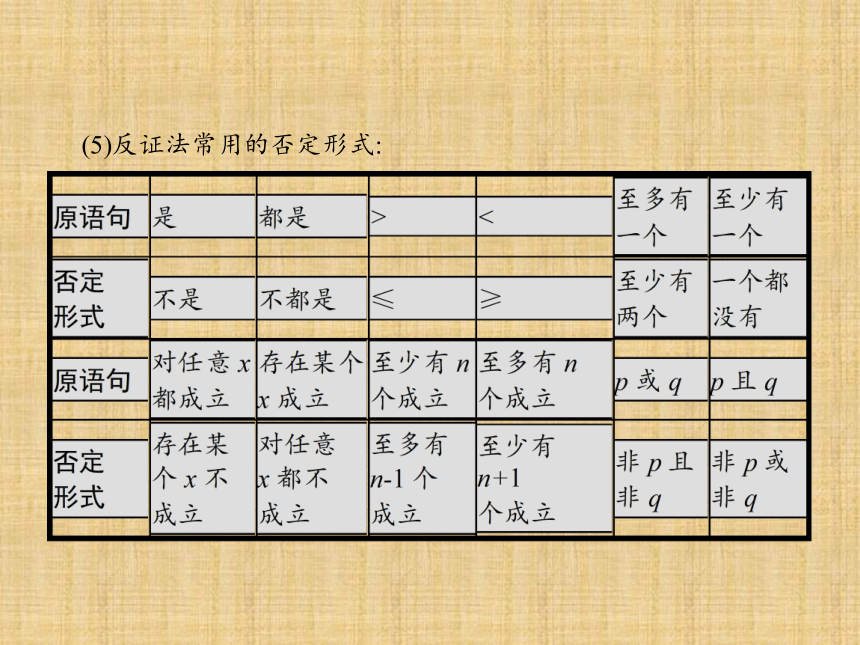
(5)反证法常用的否定形式:
【做一做1】 命题“a,b是实数,若|a-1|+|b-1|=0,则a=b=1”用反证法证明时,应假设 .?
解析:“a=b=1”是“a=1,且b=1”,又因为“p且q”的否定为“非p或非q”,所以“a=b=1”的否定为“a≠1或b≠1”.
答案:a≠1或b≠1
【做一做2】 用反证法证明命题“若x2-(a+b)x+ab≠0,则x≠a,且x≠b”时,应假设 .?
答案:x=a或x=b
如何理解反证法?
剖析:反证法证题的特征:通过导出矛盾、归结谬误,而使命题得证.
反证法的原理是“否定之否定等于肯定”.
反证法解题的实质就是否定结论导出矛盾,从而说明原结论正确,即证明命题的逆否命题成立.否定结论:对结论的反面要一一否定,不能遗漏;否定一个反面之反证法称为归谬法,否定两个或两个以上反面之反证法称为穷举法.要注意用反证法解题时,结论的否定在推理论证中可以作为已知使用,导出矛盾是指在假设的前提下,逻辑推理结果与“已知条件、假设、公理、定理或显然成立的事实”等相矛盾.
用反证法证明不等式,常用的否定形式有:“≥”的反面为“<”;“≤”的反面为“>”;“>”的反面为“≤”;“<”的反面为“≥”;“≠”的反面为“=”;“=”的反面为“≠”.
反证法属逻辑方法范畴,它的严谨体现在它的原理上,即“否定之否定等于肯定”.其中:第一个否定是指“否定结论”;第二个否定是指“逻辑推理结果否定了假设”.反证法属“间接解题方法”,书写格式易错之处是“假设”易错写成“设”.
反证法不是直接证明结论,而是先否定结论,在否定结论的基础上运用演绎推理,导出矛盾,从而肯定结论的正确性.
题型一
题型二
题型三
题型四
否定性命题的证明
【例题1】 设数列{an}是公比为q的等比数列,Sn是它的前n项和.
求证:数列{Sn}不是等比数列.
分析:本题是否定性命题,可以尝试用反证法证明.
证明:证法一:(反证法)假设数列{Sn}是等比数列,则 =S1S3,
即 (1+q)2=a1·a1(1+q+q2).
因为a1≠0,所以(1+q)2=1+q+q2,即q=0,这与q≠0矛盾,故数列{Sn}不是等比数列.
证法二:要证数列{Sn}不是等比数列,只需证明SnSn+2≠
因为Sn+1=a1+qSn,Sn+2=a1+qSn+1,
所以 (a1+qSn+1)-(a1+qSn)Sn+1=a1(Sn-Sn+1)=-a1an+1≠0.
所以数列{Sn}不是等比数列.
题型一
题型二
题型三
题型四
反思本题的解答依据是等差数列和等比数列的概念和性质,体现了特殊化思想和正难则反的思维策略.
题型一
题型二
题型四
题型三
至多、至少问题的证明
【例题2】 求证:当m为实数时,关于x的一元二次方程x2-5x+m=0与2x2+x-6-m=0至少有一个方程有实根.
分析:从正面证明难以入手,考虑应用反证法证明.
证明:假设上述两个方程都无实根,
则
因为满足①②的实数m不存在.
所以当m∈R时,所给两个方程至少有一个方程有实根.
反思凡含有“至少”“至多”等词语的命题宜采用反证法证明.
题型一
题型二
题型三
题型四
唯一性命题的证明
【例题3】 已知:直线a,b为两条相交直线.
求证:a与b有且只有一个交点.
分析:“有且只有”“唯一”等问题常考虑应用反证法证明.
证明:假设结论不成立,即有两种可能:无交点、至少有两个交点.
①若直线a,b无交点,则a∥b或a,b异面,这与已知“a,b为两条相交直线”矛盾;
②若直线a,b至少有两个交点A和B,这样同时经过点A,B就有两条直线,这与“经过两点有且只有一条直线”相矛盾.
综上所述,两条相交直线a,b有且只有一个交点.
反思结论以“有且只有”“只有一个”“唯一存在”等形式出现的命题,由于反设结论易于导出矛盾,所以用反证法证其唯一性简单明了.
题型一
题型二
题型三
题型四
易错辨析
易错点:运用反证法证明命题时,第一步否定结论易错,因为有些结论的对立面不易确定,从而出错,解决的方法是:(1)利用集合思想检验;(2)对特殊的关键词,要记住它的否定形式.
【例题4】 用反证法证明命题“若ab不是偶数,则整数a,b都不是偶数”时,应假设 .?
错解:整数a,b不都是偶数.
错因分析:整数a,b不都是偶数包括的情况是:①a是偶数,b是奇数;②a是奇数,b是偶数;③a,b都是奇数.显然,假设并不是结论的对立面,所以不正确.题目中“整数a,b都不是偶数”即“整数a,b都是奇数”,故假设为“整数a,b不都是奇数.”
正解:整数a,b不都是奇数
1 2 3 4 5
答案:D
1 2 3 4 5
2用反证法证明“自然数a,b,c中恰有一个偶数”时的正确假设为( )
A.a,b,c都是奇数
B.a,b,c都是奇数或至少有两个偶数
C.a,b,c都是偶数
D.a,b,c中至少有两个偶数
解析:a,b,c三个数的奇偶性有以下几种情况:①全是奇数;②有两个奇数,一个偶数;③有一个奇数,两个偶数;④全是偶数.因为要否定②,所以假设应为“a,b,c全是奇数或至少有两个偶数”.
答案:B
1 2 3 4 5
3两条异面直线在同一个平面内的射影不可能是( )
A.两条平行直线
B.两条相交直线
C.一点与一条直线
D.同一条直线
解析:假设两条直线在同一个平面内的射影是同一条直线,则这两条直线的位置关系为平行或相交或重合,这均与两条直线异面矛盾,故异面直线在同一个平面中的射影不可能为同一条直线.
答案:D
1 2 3 4 5
4用反证法证明命题“如果a,b∈N+,ab可被5整除,那么a,b中至少有一个能被5整除”时,假设的内容是 .?
解析:“至少有一个”的反设词是“一个都没有”,即“都不能”.
答案:a,b都不能被5整除
1 2 3 4 5
5求证:当x2+bx+c2=0有两个不相等的非零实数根时,bc≠0.
分析:bc≠0的否定形式为bc=0,包括:①b=0,c=0;②b=0,c≠0;③b≠0,c=0三种情况,故需要分类讨论.
证明:假设bc=0.
(1)若b=0,c=0,方程变为x2=0,则x1=x2=0是方程x2+bx+c2=0的两根,这与方程有两个不相等的非零实数根矛盾.
(2)若b=0,c≠0,方程变为x2+c2=0,此时方程无解,与x2+bx+c2=0有两个不相等的非零实数根矛盾.
(3)若b≠0,c=0,方程变为x2+bx=0,方程的根为x1=0,x2=-b,这与方程有两个不相等的非零实数根矛盾.
综上所述,可知bc≠0.
1.了解反证法是间接证明中最基本和最常用的一种方法.
2.熟练掌握用反证法证题的三个步骤:(1)反设;(2)归谬;(3)结论.
3.认识反证法在数学证明中的重要作用;学会用反证法证题,并能根据题目的类型合理选择证明问题的方法;学会寻找问题中的矛盾,进行正确推理.
反证法
一般地,由证明p?q转向证明????q?r?…?t,
t与假设矛盾,或与某个真命题矛盾,从而判定????q为假,推出q为真的方法,叫做反证法.
知识拓展(1)反证法的实质:证明命题的否定为假,所以命题为真.
(2)应用反证法证明数学命题的一般步骤:
①分清命题的条件和结论;
②作出与命题结论相矛盾的假定;
③由假定出发,应用正确的推理方法,推出矛盾的结果;
④断定产生矛盾结果的原因,在于开始所作的假定不真,于是原结论成立,从而间接地证明命题为真.
(3)反证法的适用情形:
①否定性命题;
②唯一性问题;
③至多至少问题.
(4)用反证法证明命题得出矛盾的方法:
①与假定矛盾;
②与数学公理、定理、公式、定义或已被证明了的结论矛盾;
③与公认的简单事实矛盾.
(5)反证法常用的否定形式:
【做一做1】 命题“a,b是实数,若|a-1|+|b-1|=0,则a=b=1”用反证法证明时,应假设 .?
解析:“a=b=1”是“a=1,且b=1”,又因为“p且q”的否定为“非p或非q”,所以“a=b=1”的否定为“a≠1或b≠1”.
答案:a≠1或b≠1
【做一做2】 用反证法证明命题“若x2-(a+b)x+ab≠0,则x≠a,且x≠b”时,应假设 .?
答案:x=a或x=b
如何理解反证法?
剖析:反证法证题的特征:通过导出矛盾、归结谬误,而使命题得证.
反证法的原理是“否定之否定等于肯定”.
反证法解题的实质就是否定结论导出矛盾,从而说明原结论正确,即证明命题的逆否命题成立.否定结论:对结论的反面要一一否定,不能遗漏;否定一个反面之反证法称为归谬法,否定两个或两个以上反面之反证法称为穷举法.要注意用反证法解题时,结论的否定在推理论证中可以作为已知使用,导出矛盾是指在假设的前提下,逻辑推理结果与“已知条件、假设、公理、定理或显然成立的事实”等相矛盾.
用反证法证明不等式,常用的否定形式有:“≥”的反面为“<”;“≤”的反面为“>”;“>”的反面为“≤”;“<”的反面为“≥”;“≠”的反面为“=”;“=”的反面为“≠”.
反证法属逻辑方法范畴,它的严谨体现在它的原理上,即“否定之否定等于肯定”.其中:第一个否定是指“否定结论”;第二个否定是指“逻辑推理结果否定了假设”.反证法属“间接解题方法”,书写格式易错之处是“假设”易错写成“设”.
反证法不是直接证明结论,而是先否定结论,在否定结论的基础上运用演绎推理,导出矛盾,从而肯定结论的正确性.
题型一
题型二
题型三
题型四
否定性命题的证明
【例题1】 设数列{an}是公比为q的等比数列,Sn是它的前n项和.
求证:数列{Sn}不是等比数列.
分析:本题是否定性命题,可以尝试用反证法证明.
证明:证法一:(反证法)假设数列{Sn}是等比数列,则 =S1S3,
即 (1+q)2=a1·a1(1+q+q2).
因为a1≠0,所以(1+q)2=1+q+q2,即q=0,这与q≠0矛盾,故数列{Sn}不是等比数列.
证法二:要证数列{Sn}不是等比数列,只需证明SnSn+2≠
因为Sn+1=a1+qSn,Sn+2=a1+qSn+1,
所以 (a1+qSn+1)-(a1+qSn)Sn+1=a1(Sn-Sn+1)=-a1an+1≠0.
所以数列{Sn}不是等比数列.
题型一
题型二
题型三
题型四
反思本题的解答依据是等差数列和等比数列的概念和性质,体现了特殊化思想和正难则反的思维策略.
题型一
题型二
题型四
题型三
至多、至少问题的证明
【例题2】 求证:当m为实数时,关于x的一元二次方程x2-5x+m=0与2x2+x-6-m=0至少有一个方程有实根.
分析:从正面证明难以入手,考虑应用反证法证明.
证明:假设上述两个方程都无实根,
则
因为满足①②的实数m不存在.
所以当m∈R时,所给两个方程至少有一个方程有实根.
反思凡含有“至少”“至多”等词语的命题宜采用反证法证明.
题型一
题型二
题型三
题型四
唯一性命题的证明
【例题3】 已知:直线a,b为两条相交直线.
求证:a与b有且只有一个交点.
分析:“有且只有”“唯一”等问题常考虑应用反证法证明.
证明:假设结论不成立,即有两种可能:无交点、至少有两个交点.
①若直线a,b无交点,则a∥b或a,b异面,这与已知“a,b为两条相交直线”矛盾;
②若直线a,b至少有两个交点A和B,这样同时经过点A,B就有两条直线,这与“经过两点有且只有一条直线”相矛盾.
综上所述,两条相交直线a,b有且只有一个交点.
反思结论以“有且只有”“只有一个”“唯一存在”等形式出现的命题,由于反设结论易于导出矛盾,所以用反证法证其唯一性简单明了.
题型一
题型二
题型三
题型四
易错辨析
易错点:运用反证法证明命题时,第一步否定结论易错,因为有些结论的对立面不易确定,从而出错,解决的方法是:(1)利用集合思想检验;(2)对特殊的关键词,要记住它的否定形式.
【例题4】 用反证法证明命题“若ab不是偶数,则整数a,b都不是偶数”时,应假设 .?
错解:整数a,b不都是偶数.
错因分析:整数a,b不都是偶数包括的情况是:①a是偶数,b是奇数;②a是奇数,b是偶数;③a,b都是奇数.显然,假设并不是结论的对立面,所以不正确.题目中“整数a,b都不是偶数”即“整数a,b都是奇数”,故假设为“整数a,b不都是奇数.”
正解:整数a,b不都是奇数
1 2 3 4 5
答案:D
1 2 3 4 5
2用反证法证明“自然数a,b,c中恰有一个偶数”时的正确假设为( )
A.a,b,c都是奇数
B.a,b,c都是奇数或至少有两个偶数
C.a,b,c都是偶数
D.a,b,c中至少有两个偶数
解析:a,b,c三个数的奇偶性有以下几种情况:①全是奇数;②有两个奇数,一个偶数;③有一个奇数,两个偶数;④全是偶数.因为要否定②,所以假设应为“a,b,c全是奇数或至少有两个偶数”.
答案:B
1 2 3 4 5
3两条异面直线在同一个平面内的射影不可能是( )
A.两条平行直线
B.两条相交直线
C.一点与一条直线
D.同一条直线
解析:假设两条直线在同一个平面内的射影是同一条直线,则这两条直线的位置关系为平行或相交或重合,这均与两条直线异面矛盾,故异面直线在同一个平面中的射影不可能为同一条直线.
答案:D
1 2 3 4 5
4用反证法证明命题“如果a,b∈N+,ab可被5整除,那么a,b中至少有一个能被5整除”时,假设的内容是 .?
解析:“至少有一个”的反设词是“一个都没有”,即“都不能”.
答案:a,b都不能被5整除
1 2 3 4 5
5求证:当x2+bx+c2=0有两个不相等的非零实数根时,bc≠0.
分析:bc≠0的否定形式为bc=0,包括:①b=0,c=0;②b=0,c≠0;③b≠0,c=0三种情况,故需要分类讨论.
证明:假设bc=0.
(1)若b=0,c=0,方程变为x2=0,则x1=x2=0是方程x2+bx+c2=0的两根,这与方程有两个不相等的非零实数根矛盾.
(2)若b=0,c≠0,方程变为x2+c2=0,此时方程无解,与x2+bx+c2=0有两个不相等的非零实数根矛盾.
(3)若b≠0,c=0,方程变为x2+bx=0,方程的根为x1=0,x2=-b,这与方程有两个不相等的非零实数根矛盾.
综上所述,可知bc≠0.
