人教版七年级数学下册5.2.1平行线课件(共43张PPT)
文档属性
| 名称 | 人教版七年级数学下册5.2.1平行线课件(共43张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-01-18 00:00:00 | ||
图片预览








文档简介
新人教版-七年级(下)数学-第五章
5 .2.1 平行线
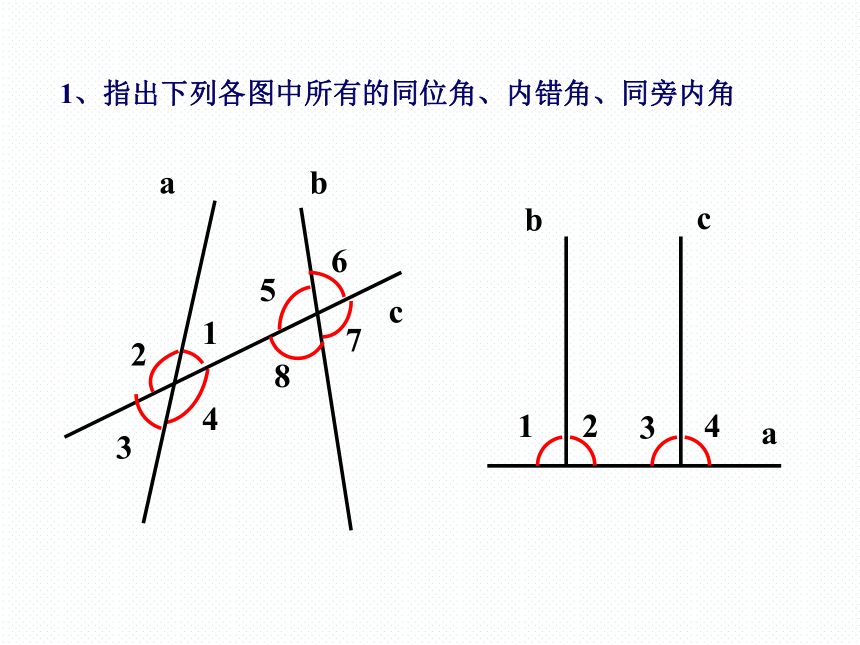
同位角、内错角、同旁内角的特点:
被截直线的同一方向
被截直线的内部
被截直线的内部
截线的同侧
截线的两侧
截线的同侧
“三线八角”回顾
与被截直线的关系 与截线的关系
同位角
内错角
同旁内角
1、指出下列各图中所有的同位角、内错角、同旁内角
二、重点和难点
1、了解两条直线的平行关系,掌握有关的符号表示。
2、学会用三角尺、量角器画平行线。
3、掌握平行线的性质。
重点:了解两条平行线的关系及有关性质。
难点:画平行线,理解平行线的含义。
一、学习目标
如图,电梯的扶手给我们什么印象?
电梯扶手所在直线会相交吗?
生活中好多事物给我们线的感觉,那么下列这些线给我们什么印象呢?
铁轨所在直线会相交吗?
那么铁轨给我们什么印象?还有什么地方给我们相同的印象呢?
双杠的两个握杠给我们什么印象?哪些地方也给我们这种印象?
生活中许多事物都给我们平行线的印象。
同一平面内,不相交的两条直线叫做平行线
平行线的定义:
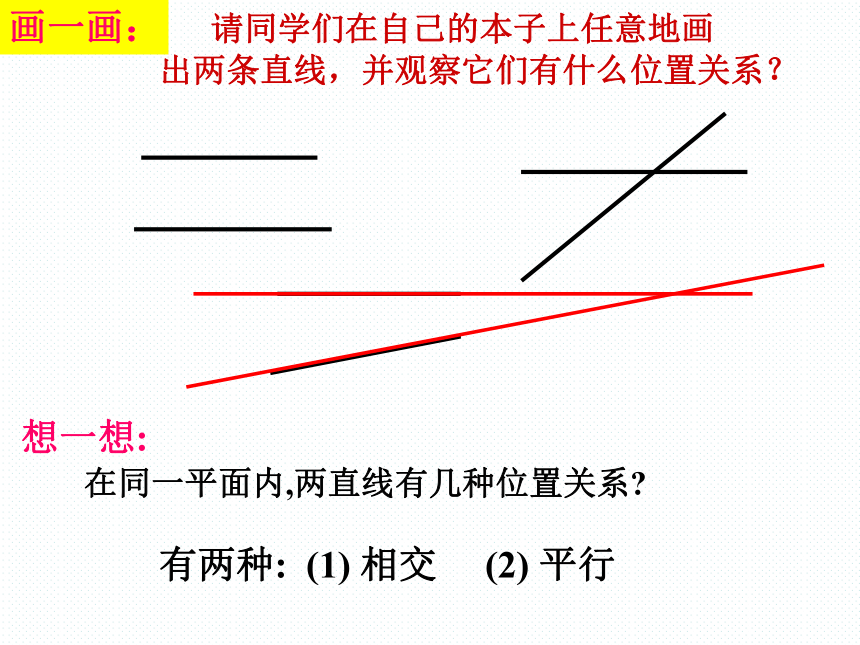
想一想:
在同一平面内,两直线有几种位置关系?
有两种: (1) 相交 (2) 平行
请同学们在自己的本子上任意地画
出两条直线,并观察它们有什么位置关系?
画一画:
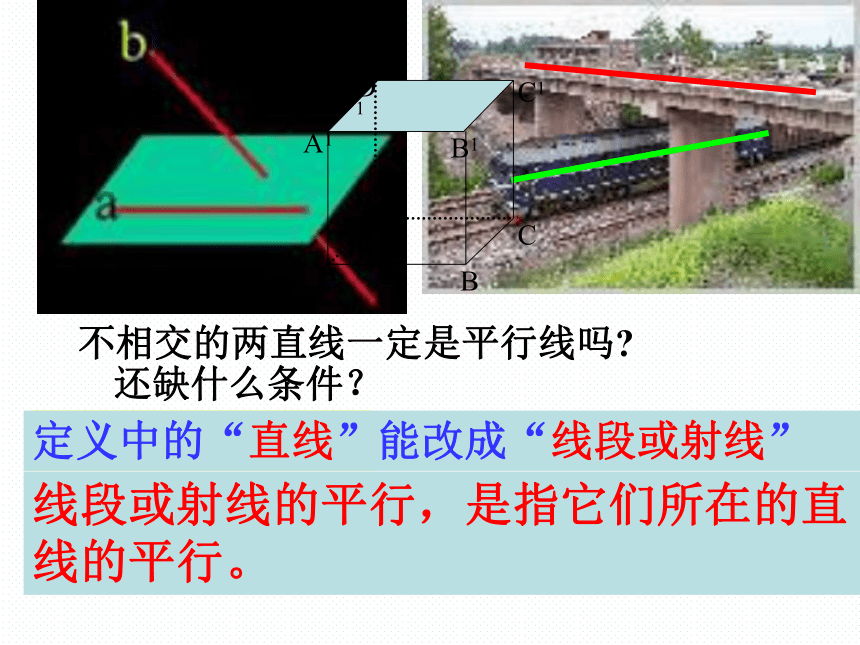
不相交的两直线一定是平行线吗?
平行线的定义:
在同一个平面内,不相交的两条直线叫做平行线。
直线
不相交
在同一个平面内
还缺什么条件?
定义中的“直线”能改成“线段或射线”吗?
线段或射线的平行,是指它们所在的直线的平行。
思考:在同一平面内,两条直线有几种位置关系?
相交
平行
垂直
定义
在同一平面内,不相交的两条直线。
符号
图形
读法
直线AB平行于直线CD
直线a平行于直线b
我们通常用符号“//”表示平行。
平行线的表示
1、判断下列说法是否正确,并说明理由。
①不相交的两条直线是平行线。
②在同一平面内,两条不相交的线段是平行线。
③过一点可以而且只可以画一条直线与已知直线平行。
AB∥ CD,AD∥ BC。
课内练习
(╳)
(╳)
(╳)
下列说法正确的是( )
A、在同一平面内,两条直线的位置关系有相交,
垂直,平行三种。
B、在同一平面内,不垂直的两直线必平行。
C、在同一平面内,不平行的两直线必垂直。
D、在同一平面内,不相交的两直线一定不垂直。
D
巩固练习
一个长方体如图,和AA'平行的棱有多少条?和AB平行的棱有多少条?请用符号把它们表示出来。
和AA'平行的棱有3条:
BB'∥AA', CC'∥AA',
DD'∥AA'.
和AB平行的棱有3条:
A'B'∥AB, C'D'∥AB,
CD∥AB.
1)观察如图所示的长方体后填空
①用符号表示下列两棱的位置关系:
A1B1____AB AA1____AB ,
A1D1____C1D1 , AD____BC
2)A1B1与BC所在的直线是两条不相交的直线,他们____平行线(填“是”或“不是”)。由此可知,在___________,两条不相交的直线才能叫平行线。
3)在同一平面内,两条不重合的直线位置关系只有_____种,即_____________。
课堂练习:
∥
⊥
⊥
∥
不是
同一平面内
2
相交和平行
思考:看着这些图形,你能画平行线?
A
B
C
D
注意:AB ⊥m, CD ⊥m 且AB=CD
m
你有什么发现吗?
试着用尺子画一个长方形
垂直于同一条直线
的两直线互相平行!
看AB和CD
1“垂直法”:
1.任意画一条直线m,使m⊥AB
2. 画直线 n⊥m
则n//AB,n就是所要画的直线
Q
平行线的画法1:
n
平行线的画法2:
“推平行线法”:
已知直线AB,画一条直线和已知直线AB平行
A
B
若将此处的直角改为锐角
将会怎样
一、放
二、靠
三、推
四、画
平行线的画法2:
“推平行线法”:
●
一、放
二、靠
三、推
四、画
过点P能否再画一条直线与AB平行?
例:已知直线AB和直线外一点P,过点P画一条直线和已知直线 AB平行。
P
推平行线法
A
B
如图,在△ABC中,P是边AC上一点.过点P分别画AB、BC的平行线
A
B
C
.P
现学现卖
经过直线外一点,有且只有一条直线与这条直线平行。
平行公理:
想一想
·
A
B
C
B
平面内
(垂直)
(唯一性)
问题:经过点C能画出几条直线与直线AB平行?
说明:人们在长期实践中总结出来的结论叫基本事实,也称为公理,它可以作为以后推理的依据.
一般地, 经过直线外一点,有且只有一条直线平行于已知直线。
结 论:
(1)你能在右图中的方格中画出平行线吗?
方法:
①利用方格纸中的直线画平行线。
②利用格点(长方形的对角线)画平行线。
(2)若改方格纸为白纸,你能利用以下哪些工具:①直尺 ②三角板 ③量角器能画已知直线AB的平行线?能画多少条?
试一试
推平行线法
可以画无数条
如图:三条直线a、b、c。如果a//c,b//c,
那么直线a与b有什么关系?
F
E
b
a
假设a与b相交,
设a与b相交于O
因为a//c,b//c
于是过点O就有两条直线a
b都与c平行。
根据平行公理,这是不可能的
也就是说,a与b不能相交,
只能平行。
//
//
//
//
(平行线的传递性)
a//c,
b//c;
a//b
推论:如果两条直线都平行于第三条直线,那么这两条直线也互相平行.
几何语言表达:
?
?
(如果两条直线都和第三条直线平行,
那么这两条直线也互相平行)
(如果两条直线都平行于第三条直线,那么这两条直线也互相平行)
∴ AB//CD
(已知)
∵ AB//EF, CD//EF
如图,直线a ∥b,b∥c,c∥d,那么a ∥d吗?为什么?
解: 因为 a ∥b,b∥c,
所以 a ∥c ( )
如果两条直线都与第三条直线平行,那么这两条直线互相平行
如果两条直线都与第三条直线平行,那么这两条直线互相平行
因为 c∥d,
所以 a ∥d
( )
a
b
C
如果a⊥c, a⊥b;
那么b//c
如果两条直线都垂直于第三条直线,那么这两条直线互相平行.
(2)、观察直线 b、c是否平行?
(1)画一条直线 a,再画两条直线
b、c分别与直线a垂直。
探究:
(2)A1B1与BC所在的直线是两条不相交的直线,它们_____平行线(填“是”或“不是”),由此可知,在____内,两条不相交的直线才能叫平行线
(1)用符号表示下列两棱的位置关系:
A1B1___AB ,AA1____AB ,A1D1____C1D1 ,AD___BC。
练一练
不是
同一平面
∥
⊥
⊥
∥
1. 不相交的两条直线叫做平行线.( )
(3)判断题
×
2. 在同一平面内,两条不平行的直线必相交 . ( )
√
3.有且只有一个公共点的两条直线是相交直线。( )
√
5.作已知直线的平行线只能作一条。 ( )
×
6.在同一平面内不相交的两条线段必平行. ( )
×
4.没有公共点的两条直线 是平行线。( )
×
(0个,1个,2个或3个)
1、下列说法正确的是( )
A、在同一平面内,不相交的两条射线是平行线;
B、在同一平面内,不相交的两条线段是平行线;
C、在同一平面内,两条直线的位置关系不相交就平行;
D、不相交的两条直线是平行线
C
做一做
2、平面内的5条直线,如要使它们出现5个交点,怎样安排才能办到?画图说明。
做
一
做
1、下列说法正确的个数是( )
(1)两条直线不相交就平行。
(2)在同一平面内,两条平行的直线有且只有一个交点
(3)过一点有且只有一条直线与已知直线平行
(4)平行于同一直线的两条直线互相平行
(5)两直线的位置关系只有相交与平行
A、0 B、1 C、2 D、4
B
2、下列推理正确的是( )
A、因为a // d,b // c,所以c // d;
B、因为a // c,b // d,所以c // d;
C、因为a // b,a // c,所以b // c;
D、因为a // b,c // d,所以a // c。
C
经过直线外一点,有且只有一条直线与已知直线平行。
4、下列说法正确的是( )
A、一条直线的平行线有且只有一条
B、经过一点有且只有一条直线与已知直线平行
C、经过一点有两条直线与某一直线平行
D、过直线外一点有且只有一条直线与已知直线平行
D
5、完成下列推理,并在括号内注明理由。
(1)如图1所示,因为AB // DE,BC // DE(已知)。所以
A,B,C三点___________( )
(2)如图2所示,因为AB // CD,CD // EF(已知),所以
________ // _________( )
·
·
·
A
D
E
B
C
图 1
在同一直线上
经过直线外一点,有且只有一条直线与这条直线平行
AB
EF
如果两条直线都和第三条直线平行,
那么这两条直线也互相平行
6、如图所示,
(1)过BC上任意一点P画AB的平行线交AC于T;
(2)过C画MN//AB;
(3)直线PT,MN是何种位置关系?试说明理由。
A
B
C
P
用数学知识来解决现实生活中的问题:
建筑工人要测验墙壁是否竖直,如图3所示,可先在一条狭长的木板上面画一直线a,使其平行于木板的一边,再在线的上端O处钉一只钉子,挂下一条铅垂线OP,然后把板的这一边紧贴墙壁,这时如果OP能跟a线重合,则墙壁便是竖直的,为什么?
图 3
小结:
1、平行线的定义:
同一平面内,不相交的两条直线叫做平行线
2、平行线的表示法
通常用符号“//”表示平行。
AB//CD或a//b
3、平行线的两条性质
平面内,经过直线外一点,有且只有一条直线与这条直线平行。
平行公理:
(唯一性)
推论:如果两条直线都平行于第三条直线,那么这两条直线也互相平行.
(平行线的传递性)
如果a//c,
b//c;
那么a//b
祝同学们学习进步
5 .2.1 平行线
同位角、内错角、同旁内角的特点:
被截直线的同一方向
被截直线的内部
被截直线的内部
截线的同侧
截线的两侧
截线的同侧
“三线八角”回顾
与被截直线的关系 与截线的关系
同位角
内错角
同旁内角
1、指出下列各图中所有的同位角、内错角、同旁内角
二、重点和难点
1、了解两条直线的平行关系,掌握有关的符号表示。
2、学会用三角尺、量角器画平行线。
3、掌握平行线的性质。
重点:了解两条平行线的关系及有关性质。
难点:画平行线,理解平行线的含义。
一、学习目标
如图,电梯的扶手给我们什么印象?
电梯扶手所在直线会相交吗?
生活中好多事物给我们线的感觉,那么下列这些线给我们什么印象呢?
铁轨所在直线会相交吗?
那么铁轨给我们什么印象?还有什么地方给我们相同的印象呢?
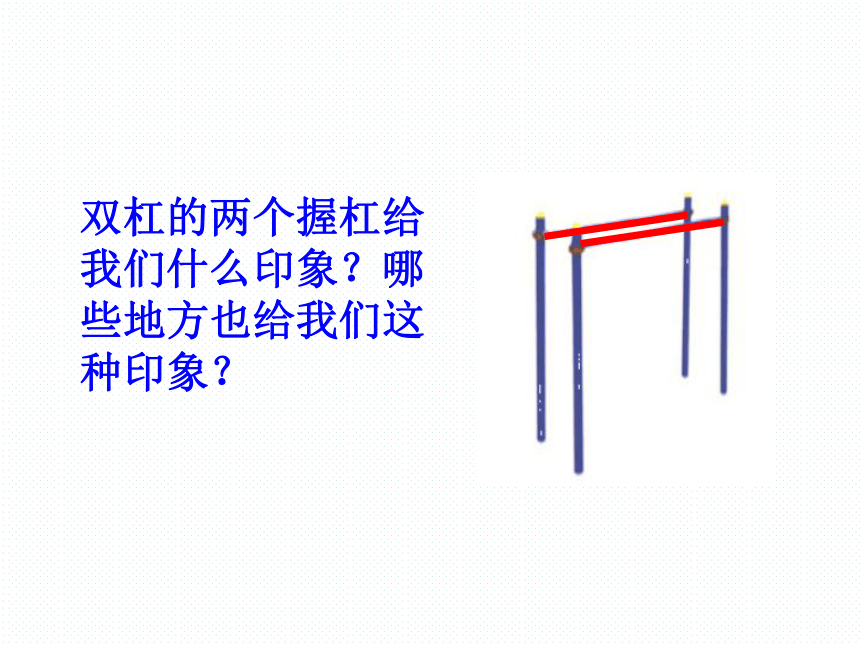
双杠的两个握杠给我们什么印象?哪些地方也给我们这种印象?
生活中许多事物都给我们平行线的印象。
同一平面内,不相交的两条直线叫做平行线
平行线的定义:
想一想:
在同一平面内,两直线有几种位置关系?
有两种: (1) 相交 (2) 平行
请同学们在自己的本子上任意地画
出两条直线,并观察它们有什么位置关系?
画一画:
不相交的两直线一定是平行线吗?
平行线的定义:
在同一个平面内,不相交的两条直线叫做平行线。
直线
不相交
在同一个平面内
还缺什么条件?
定义中的“直线”能改成“线段或射线”吗?
线段或射线的平行,是指它们所在的直线的平行。
思考:在同一平面内,两条直线有几种位置关系?
相交
平行
垂直
定义
在同一平面内,不相交的两条直线。
符号
图形
读法
直线AB平行于直线CD
直线a平行于直线b
我们通常用符号“//”表示平行。
平行线的表示
1、判断下列说法是否正确,并说明理由。
①不相交的两条直线是平行线。
②在同一平面内,两条不相交的线段是平行线。
③过一点可以而且只可以画一条直线与已知直线平行。
AB∥ CD,AD∥ BC。
课内练习
(╳)
(╳)
(╳)
下列说法正确的是( )
A、在同一平面内,两条直线的位置关系有相交,
垂直,平行三种。
B、在同一平面内,不垂直的两直线必平行。
C、在同一平面内,不平行的两直线必垂直。
D、在同一平面内,不相交的两直线一定不垂直。
D
巩固练习
一个长方体如图,和AA'平行的棱有多少条?和AB平行的棱有多少条?请用符号把它们表示出来。
和AA'平行的棱有3条:
BB'∥AA', CC'∥AA',
DD'∥AA'.
和AB平行的棱有3条:
A'B'∥AB, C'D'∥AB,
CD∥AB.
1)观察如图所示的长方体后填空
①用符号表示下列两棱的位置关系:
A1B1____AB AA1____AB ,
A1D1____C1D1 , AD____BC
2)A1B1与BC所在的直线是两条不相交的直线,他们____平行线(填“是”或“不是”)。由此可知,在___________,两条不相交的直线才能叫平行线。
3)在同一平面内,两条不重合的直线位置关系只有_____种,即_____________。
课堂练习:
∥
⊥
⊥
∥
不是
同一平面内
2
相交和平行
思考:看着这些图形,你能画平行线?
A
B
C
D
注意:AB ⊥m, CD ⊥m 且AB=CD
m
你有什么发现吗?
试着用尺子画一个长方形
垂直于同一条直线
的两直线互相平行!
看AB和CD
1“垂直法”:
1.任意画一条直线m,使m⊥AB
2. 画直线 n⊥m
则n//AB,n就是所要画的直线
Q
平行线的画法1:
n
平行线的画法2:
“推平行线法”:
已知直线AB,画一条直线和已知直线AB平行
A
B
若将此处的直角改为锐角
将会怎样
一、放
二、靠
三、推
四、画
平行线的画法2:
“推平行线法”:
●
一、放
二、靠
三、推
四、画
过点P能否再画一条直线与AB平行?
例:已知直线AB和直线外一点P,过点P画一条直线和已知直线 AB平行。
P
推平行线法
A
B
如图,在△ABC中,P是边AC上一点.过点P分别画AB、BC的平行线
A
B
C
.P
现学现卖
经过直线外一点,有且只有一条直线与这条直线平行。
平行公理:
想一想
·
A
B
C
B
平面内
(垂直)
(唯一性)
问题:经过点C能画出几条直线与直线AB平行?
说明:人们在长期实践中总结出来的结论叫基本事实,也称为公理,它可以作为以后推理的依据.
一般地, 经过直线外一点,有且只有一条直线平行于已知直线。
结 论:
(1)你能在右图中的方格中画出平行线吗?
方法:
①利用方格纸中的直线画平行线。
②利用格点(长方形的对角线)画平行线。
(2)若改方格纸为白纸,你能利用以下哪些工具:①直尺 ②三角板 ③量角器能画已知直线AB的平行线?能画多少条?
试一试
推平行线法
可以画无数条
如图:三条直线a、b、c。如果a//c,b//c,
那么直线a与b有什么关系?
F
E
b
a
假设a与b相交,
设a与b相交于O
因为a//c,b//c
于是过点O就有两条直线a
b都与c平行。
根据平行公理,这是不可能的
也就是说,a与b不能相交,
只能平行。
//
//
//
//
(平行线的传递性)
a//c,
b//c;
a//b
推论:如果两条直线都平行于第三条直线,那么这两条直线也互相平行.
几何语言表达:
?
?
(如果两条直线都和第三条直线平行,
那么这两条直线也互相平行)
(如果两条直线都平行于第三条直线,那么这两条直线也互相平行)
∴ AB//CD
(已知)
∵ AB//EF, CD//EF
如图,直线a ∥b,b∥c,c∥d,那么a ∥d吗?为什么?
解: 因为 a ∥b,b∥c,
所以 a ∥c ( )
如果两条直线都与第三条直线平行,那么这两条直线互相平行
如果两条直线都与第三条直线平行,那么这两条直线互相平行
因为 c∥d,
所以 a ∥d
( )
a
b
C
如果a⊥c, a⊥b;
那么b//c
如果两条直线都垂直于第三条直线,那么这两条直线互相平行.
(2)、观察直线 b、c是否平行?
(1)画一条直线 a,再画两条直线
b、c分别与直线a垂直。
探究:
(2)A1B1与BC所在的直线是两条不相交的直线,它们_____平行线(填“是”或“不是”),由此可知,在____内,两条不相交的直线才能叫平行线
(1)用符号表示下列两棱的位置关系:
A1B1___AB ,AA1____AB ,A1D1____C1D1 ,AD___BC。
练一练
不是
同一平面
∥
⊥
⊥
∥
1. 不相交的两条直线叫做平行线.( )
(3)判断题
×
2. 在同一平面内,两条不平行的直线必相交 . ( )
√
3.有且只有一个公共点的两条直线是相交直线。( )
√
5.作已知直线的平行线只能作一条。 ( )
×
6.在同一平面内不相交的两条线段必平行. ( )
×
4.没有公共点的两条直线 是平行线。( )
×
(0个,1个,2个或3个)
1、下列说法正确的是( )
A、在同一平面内,不相交的两条射线是平行线;
B、在同一平面内,不相交的两条线段是平行线;
C、在同一平面内,两条直线的位置关系不相交就平行;
D、不相交的两条直线是平行线
C
做一做
2、平面内的5条直线,如要使它们出现5个交点,怎样安排才能办到?画图说明。
做
一
做
1、下列说法正确的个数是( )
(1)两条直线不相交就平行。
(2)在同一平面内,两条平行的直线有且只有一个交点
(3)过一点有且只有一条直线与已知直线平行
(4)平行于同一直线的两条直线互相平行
(5)两直线的位置关系只有相交与平行
A、0 B、1 C、2 D、4
B
2、下列推理正确的是( )
A、因为a // d,b // c,所以c // d;
B、因为a // c,b // d,所以c // d;
C、因为a // b,a // c,所以b // c;
D、因为a // b,c // d,所以a // c。
C
经过直线外一点,有且只有一条直线与已知直线平行。
4、下列说法正确的是( )
A、一条直线的平行线有且只有一条
B、经过一点有且只有一条直线与已知直线平行
C、经过一点有两条直线与某一直线平行
D、过直线外一点有且只有一条直线与已知直线平行
D
5、完成下列推理,并在括号内注明理由。
(1)如图1所示,因为AB // DE,BC // DE(已知)。所以
A,B,C三点___________( )
(2)如图2所示,因为AB // CD,CD // EF(已知),所以
________ // _________( )
·
·
·
A
D
E
B
C
图 1
在同一直线上
经过直线外一点,有且只有一条直线与这条直线平行
AB
EF
如果两条直线都和第三条直线平行,
那么这两条直线也互相平行
6、如图所示,
(1)过BC上任意一点P画AB的平行线交AC于T;
(2)过C画MN//AB;
(3)直线PT,MN是何种位置关系?试说明理由。
A
B
C
P
用数学知识来解决现实生活中的问题:
建筑工人要测验墙壁是否竖直,如图3所示,可先在一条狭长的木板上面画一直线a,使其平行于木板的一边,再在线的上端O处钉一只钉子,挂下一条铅垂线OP,然后把板的这一边紧贴墙壁,这时如果OP能跟a线重合,则墙壁便是竖直的,为什么?
图 3
小结:
1、平行线的定义:
同一平面内,不相交的两条直线叫做平行线
2、平行线的表示法
通常用符号“//”表示平行。
AB//CD或a//b
3、平行线的两条性质
平面内,经过直线外一点,有且只有一条直线与这条直线平行。
平行公理:
(唯一性)
推论:如果两条直线都平行于第三条直线,那么这两条直线也互相平行.
(平行线的传递性)
如果a//c,
b//c;
那么a//b
祝同学们学习进步
