2018-2019学年上海市浦东新区华师大二附中高二(上)期中数学试卷(解析版)
文档属性
| 名称 | 2018-2019学年上海市浦东新区华师大二附中高二(上)期中数学试卷(解析版) |  | |
| 格式 | zip | ||
| 文件大小 | 124.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-01-17 19:26:05 | ||
图片预览




文档简介
2018-2019学年上海市浦东新区华师大二附中高二(上)期中数学试卷
一、选择题(本大题共4小题,共16.0分)
设f(x)=
1
1
1
??
?1
1
??
2
1
1
(x∈R),则方程f(x)=0的解集为( )
A. {1} B. {?1,1} C. {?1} D. 以上答案均不对
若x、y满足约束条件
??+??≥1
?????≥?1
2?????≤2
目标函数z=ax+2y仅在点(1,0)处取得最小值,则a的取值范围是( )
A. (?4,2) B. (?1,2) C. (?4,0) D. (?2,4)
若分别为P(1,0)、Q(2,0),R(4,0)、S(8,0)四个点各作一条直线,所得四条直线恰围成正方形,则该正方形的面积不可能为( )
A.
16
17
B.
36
5
C.
64
37
D.
196
53
对任意两个非零的平面向量
??
和
??
,定义
??
?
??
=
|
??
|
|
??
|
????????,其中θ为
??
和
??
的夹角,若两个非零的平面向量
??
和
??
满足:①|
??
|≥|
??
|;②
??
和
??
的夹角??∈(0,
??
4
);③
??
?
??
和
??
?
??
的值都在集合{??|??=
??
2
,??∈??}中,则
??
?
??
的值为( )
A.
5
2
B.
3
2
C. 1 D.
1
2
二、填空题(本大题共10小题,共40.0分)
已知一个关于x,y的二元线性方程组
?4??+???5=0
2??????3=0
,则此线性方程组的增广矩阵为______.
已知直角坐标平面内的两个向量
??
=(1,m),
??
=(2,4)使得平面内的任意一个向量
??
都可以唯一分解成
??
=λ
??
+??
??
,则m的取值范围是______.
直线x+3y+2=0与4x+2y-1=0的夹角是______.
设向量
??
=(3,0),
??
=(2,6),则
??
在
??
上的投影为______.
如果直线3x-2y-3=0与直线6x+my+1=0平行,则它们之间的距离为______.
直线mx+4y-2=0与直线2x-5y+n=0相互垂直,垂足为(1,p),则n=______.
若原点在直线L上的射影为(2,1),直线L的倾斜角为θ,则sin2θ=______.
经过点A(-3,1)和点B(4,-2)的直线l的点方向式方程是______.
在矩形ABCD中,AB=
2
,BC=2,点E为BC的中点,点F在边CD上,若
????
?
????
=
2
,则
????
?
????
的值为______.
已知向量
??
,
??
满足|
??
|=1,|
??
|=2,若对任意单位向量
??
,均有则|
??
?
??
|+|
??
?
??
|≤
7
,则
??
?
??
最大值为______.
三、解答题(本大题共4小题,共44.0分)
用矩阵行列式的知识解关于x,y的方程组
??+????=2??
????+??=??+1
,(m∈R)
(1)求点(-l,3)关于直线x-2y-2=0的对称点坐标; (2)求直线y=
??
2
-1关于直线y=2x-4的对称直线的一般式方程.
已知向量|
??
|=
8
15
,|
??
|=
4
15
. (1)若
??
,
??
的夹角为60°,{
??
|x
??
+??
??
=
??
,|
??
|=1,xy>0},求x,y所满足的关系式,并求xy的最大值; (2)若对任意的(x,y)∈{(x,y)||x
??
+y
??
|=1,xy>0),都有|x+y|≤1成立,求
??
?
??
的最小值.
如果从北大打车到北京车站去接人,聪明的专家一定会选择走四环.虽然从城中间直穿过去看上去很诱人,但考虑到北京的道路几乎总是正南正北的方向,事实上不会真有人认为这样走能抄近路.在城市中,专家估算两点之间的距离时,不会直接去测量两点之间的直线距离,而会去考虑它们相距多少个街区.在理想模型中,假设每条道路都是水平或者竖直的,那么只要你朝着目标走(不故意绕远路),不管你这样走,花费的路程都是一样的.出租车几何学(taxicabgeometry),所谓的“出租车几何学”是由十九世纪的另一位真专家赫尔曼-闵可夫斯基所创立的,在出租车几何学中,点还是形如(x,y)的有序实数对,直线还是满足ax+by+c=0的所有(x,y)组成的图形,角度大小的定义也和原米一样.只是直角坐标系内任意两点A(x1,y1),B(x2,y2)定义它们之间的一种“距离”:||AB||=|x1-x2|+|y1-y2|,请解决以下问题: (1)定义:“圆”是所有到定点“距离”为定值的点组成的图形,求“圆周”上的所有点到点Q(a,b)的“距离”均为r的“圆”方程,并作出大致图象 (2)在出租车几何学中,到两点A、B“距离”相等的点的轨迹称为线段AB的“垂直平分线”,已知点A(1,3)、B(6,9),C(1,9) ①写出在线段AB的“垂直平分线”的轨迹方程,并写出大致图象; ②求证:△ABC三边的“垂直平分线”交于一点(该点称为△ABC的“外心”),并求出△ABC的“外心”,
答案和解析
1.【答案】B 【解析】
解:因为设f(x)=(x∈R),得到方程f(x)=0, 即=0, 化简得:1×(-1)×1+1×1×x2+x×1×1-x2×(-1)×1-x×1×1-1×1×1=0 化简得:x2=1 解得:x1=1,x2=-1. 故选:B. 此题要求方程的解集,主要还是化简方程左边的行列式得一元二次方程求出x即可. 此题考查学生化简行列式的能力,解方程的能力,属于基础题
2.【答案】A 【解析】
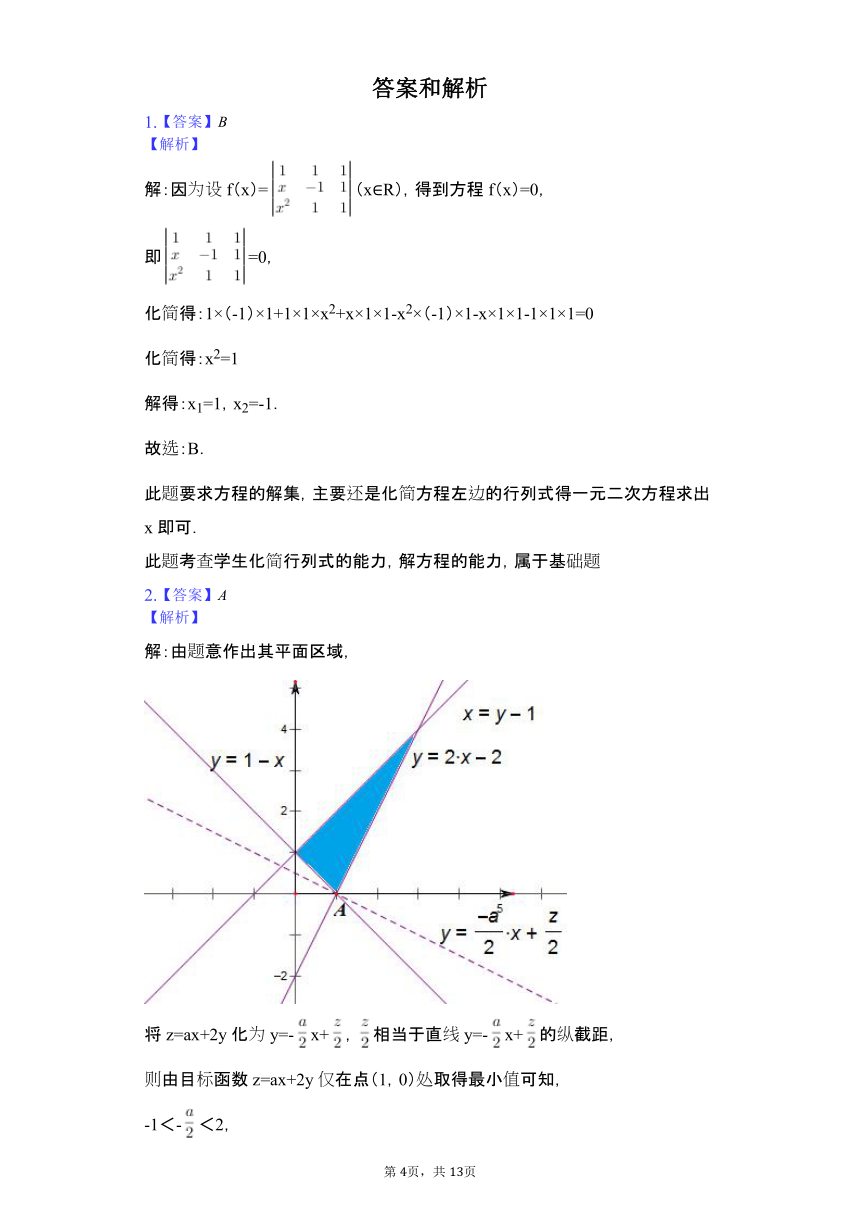
解:由题意作出其平面区域, 将z=ax+2y化为y=-x+,相当于直线y=-x+的纵截距, 则由目标函数z=ax+2y仅在点(1,0)处取得最小值可知, -1<-<2, 则-4<a<2, 故选:A. 由题意作出其平面区域,将z=ax+2y化为y=-x+,相当于直线y=-x+的纵截距,由几何意义可得. 本题考查了简单线性规划,作图要细致认真,属于中档题.
3.【答案】C 【解析】
解:如果过点P(1,0),Q(2,0),R(4,0),S(8,0)作四条直线构成一个正方形, 过P点的必须和过Q,R,S的其中一条直线平行和另外两条垂直, 假设过P点和Q点的直线相互平行时,如图, 设直线PC与x轴正方向的夹角为θ,再过Q作它的平行线QD,过R、S作它们的垂线RB、SC,过点A作x轴的平行线分别角PC、SC于点M、N, 则AB=AMsinθ=PQsinθ=sinθ,AD=ANcosθ=RScosθ=4cosθ, 因为AB=AD,所以sinθ=4cosθ,则tanθ=4, 所以正方形ABCD的面积S=AB?AD=4sinθcosθ===, 同理可求,当直线PC和过R的直线平行时正方形ABCD的面积S为, 当直线PC和过S点的直线平行时正方形ABCD的面积S为, 故选:C. 根据题意画出图形,由图形和同角三角函数的基本关系求出正方形面积. 本题考查同角三角函数的基本关系,以及数形结合思想,属于中档题.
4.【答案】B 【解析】
解:∵=cosθ=,=cosθ=,m∈N, 由与的夹角θ∈(0,),知cos2θ=∈(,1), 故mn=3,m,n∈N, ∵, ∴0<=<1, ∴m=1,n=3, ∴=, 故选:B. 根据新定义求出=cosθ=,=cosθ=,m∈N,再根据夹角的范围求出mn=3,m,n∈N,再根据第1个条件,即可求出m,n的值,问题得以解决 本题主要考查两个向量的数量积的定义,求得 m=1,n=3,是解题的关键,属于中档题.
5.【答案】
2
?1
3
?4
1
5
【解析】
解:由增广矩阵的定义:增广矩阵就是在系数矩阵的右边添上一列,这一列是方程组的等号右边的值 可直接写出增广矩阵为. 故答案为:. 首先要知道增广矩阵的定义增广矩阵就是在系数矩阵的右边添上一列,这一列是方程组的等号右边的值然后直接求解可得. 此题主要考查方程组增广矩阵的定义及求法,属于基础题.
6.【答案】m≠2 【解析】
解:因为平面内的任意一个向量都可以唯一分解成=λ+μ, 所以向量与能作为基底,所以与不共线, 所以1×4-m×2≠0,解得m≠2, 故答案为:m≠2. 根据平面向量基本定理得,与必为基底,不共线. 本题考查了平面向量的基本定理.属基础题.
7.【答案】
??
4
【解析】
解:直线x+3y+2=0的斜率k1=,直线4x+2y-1=0的斜率k2=-2; 直线x+3y+2=0与4x+2y-1=0的夹角为θ, 可得tanθ=||=1, ∴θ=; 即直线x+3y+2=0与4x+2y-1=0的夹角为. 故答案为:. 直接根据夹角公式即可求解; 本题考查了直线的斜率和夹角公式的计算.属于基础题.
8.【答案】2 【解析】
解:因为向量在上的投影为:==2, 故答案为:2. 根据向量在向量上投影的概念,代入坐标计算可得. 本题考查了平面向量数量积的性质及其运算.属基础题.
9.【答案】
7
13
26
【解析】
解:直线3x-2y-3=0与直线6x+my+1=0平行,∴,解得m=-4. ∴直线6x+my+1=0化为3x-2y+=0, ∴它们之间的距离==. 故答案为:. 利用相互平行的直线斜率之间的关系、平行线之间的距离公式即可得出. 本题考查了相互平行的直线斜率之间的关系、平行线之间的距离公式,属于基础题.
10.【答案】-12 【解析】
解:∵直线mx+4y-2=0与直线2x-5y+n=0垂直,垂足为(1,p), ∴-×=-1,2-5p+n=0,m+4p-2=0, 解得m=10,p=-2,n=-12, 故答案为:-12 利用两条直线相互垂直的充要条件、直线的交点即可得出. 本题考查了两条直线相互垂直的充要条件、直线的交点,考查了推理能力与计算能力,属于基础题.
11.【答案】?
4
5
【解析】
解:原点在直线L上的射影为(2,1),∴垂线的斜率为=, ∴直线L的斜率为, ∴直线L的蝎女为-2. 设直线L的倾斜角为θ,则tanθ=-2,则sin2θ===-, 故答案为:-. 先求出垂线的斜率,可得直线L的斜率,再利用二倍角的正弦公式、同角三角函数的基本关系求得sin2θ的值. 本题主要考查直线的倾斜角和斜率,两条直线垂直的性质,用二倍角的正弦公式、同角三角函数的基本关系,属于基础题.
12.【答案】
??+3
7
=
???1
?3
【解析】
解:直线的方向向量为=(4,-2)-(-3,1)=(7,-3), 故直线l的点方向式方程是, 故答案为:. 先求出直线的方向向量的坐标,再根据直线上的一个点的坐标,即可得到直线的点方向式方程. 本题考查求直线的点方向式方程,求出直线的方向向量的坐标,是解题的关键.
13.【答案】
2
【解析】
解:∵=+, ∴=====, ∴=1,=, ∴=()?()=+=(-1)+1×2=, 故答案为:. 根据所给的图形,把已知向量用矩形的边所在的向量来表示,做出要用的向量的模长,表示出要求得向量的数量积,注意应用垂直的向量数量积等于0,得到结果. 本题考查平面向量的数量积的运算.本题解题的关键是把要用的向量表示成已知向量的和的形式,本题是一个中档题目.
14.【答案】1 【解析】
解:由||+||,可得 即对任意单位向量,向量在上的投影与向量在上的投影的和小于等于 当与共线时取等号, ∴, ∴. ∴≤1 故答案为:1 由已知可得,结合向量投影的定义及向量共线的定义可求 本题主要考查了平面向量的数量积,模长公式的应用及向量的投影的定义的简单应用.
15.【答案】解:关于x,y的方程组
??+????=2??
????+??=??+1
, ∴D=
??
1
1
??
=m2-1, 当D=m2-1≠0,即m≠1且m≠-1时, x=
1
??
1
??+1
??
2??
=
??
??+1
, y=
1
??
??
??+1
1
2??
=
2??+1
??+1
; 方程组有唯一的解
??=
??
??+1
??=
2??+1
??+1
; 当D=m2-1=0,即m=-1或m=1时, 若m=-1,则原方程组无解; 若m=1,则原方程组有无数个解. 【解析】
计算D=,讨论D≠0时方程组有唯一的解,D=0时方程组无解或有无数个解. 本题考查了二元一次方程组的行列式矩阵形式的解法及应用问题,是基础题.
16.【答案】解:(1)设点(-l,3)关于直线x-2y-2=0的对称点坐标为(x,y); 可得
3???
??+1
?
1
2
=?1,……① 中点坐标(
???1
2
,
3+??
2
)在直线x-2y-2=0上, 即
???1
2
?2×
3+??
2
?2=0……② 由①②解得解x=
13
5
,y=
?21
5
故得对称点坐标为(
13
5
,
?21
5
). (2)由题意, 联立
??=
1
2
???1
??=2???4
,可得坐标为(2,0), 对称直线的方程为:y=k(x-2),即kx-y-2k=0 在直线y=2x-4取点(3,2), 点到直线距离相等, 即
|
3
2
?2?1|
1
4
+1
=
|3???2?2??|
??
2
+1
, 解得:k=
1
2
(舍去),k=-
11
2
. ∴所求对称直线方程为.?
11
2
x-y+11=0,即11x+2y-22=0. 【解析】
(1)设点(-l,3)关于直线x-2y-2=0的对称点坐标为(x,y);可得,结合中点坐标在直线上,求解x,y可得答案; (2)联立直线y=-1与直线y=2x-4求解交点,在直线y=2x-4取点(3,2),设对称直线方程,利用点到直线距离相等求解即可; 本题考查了直线关于直线的对称直线方程的求法,考查了点到直线距离公式的运用,是基础题.
17.【答案】解:(1)∵|
??
|=
8
15
,|
??
|=
4
15
,
??
,
??
的夹角为60°, ∴
??
?
??
=
8
15
×
4
15
×
1
2
=
16
15
, 又∵x
??
+??
??
=
??
,|
??
|=1,xy>0, ∴
??
2
=
??
2
??
2
+
??
2
??
2
+2????
??
?
??
, ∴
64
??
2
15
+
16
??
2
15
+
32
15
????=1, ∴64x2+16y2+32xy=15, ∵64x2+16y2≥64xy(当且仅当8x=4y即y=2x时取等号) ∴15-32xy≥64xy, ∴xy≤
5
32
, 故xy的最大值
5
32
; (2)设
??
,
??
的夹角为θ, 由|x
??
+y
??
|=1,xy>0可得
64
15
??
2
+
16
15
??
2
+
64
15
????cosθ=1, 即64x2+16y2+64xycosθ=15, ∴cosθ=
15?64
??
2
?16
??
2
64????
∵|x+y|≤1, ∴1≥(x+y)2, ∴∴cosθ=
15?64
??
2
?16
??
2
64????
≥
15(??+??
)
2
?64
??
2
?16
??
2
64????
=
?49
??
2
?
??
2
+30????
64????
恒成立, =
?49
??
2
?
??
2
+30????
64????
=
15
32
?(
49??
64??
+
??
64??
)≤
15
32
?2
49??
64??
?
??
64??
=
1
4
当且仅当
49??
64??
=
??
64??
即y=7x时取等号, 此时
??
?
??
取得最小值
8
15
【解析】
(1)由已知可求,结合已知x=及||=1,两边同时平方,结合基本不等式即可求解; (2)设,的夹角为θ,由|x+y|=1,两边时平方,可求cosθ,然后由|x+y|≤1,可得1≥(x+y)2,代入到cosθ的表达式,进行分离后利用基本不等式即可求解. 本题主要考查了平面向量的线性运算和平面向量的数量积的运算性质的简单应用,属于知识的简单综合.
18.【答案】解:(1)“圆”是所有到定点“距离”为定值的点组成的图形, ∴“圆周”上的所有点到点Q(a,b)的“距离”均为r, ∴“圆”方程为:|x-a|+|y-b|=r; (2)①由已知条件得|x-1|+|y-3|=|x-6|+|y-9|, 若x≤1,则y=8.5; 若1<x≤6,则x+y=9.5; 若x>6,则y=3.5; 画出图象如图1所示; ①写出在线段AB的“垂直平分线”的轨迹方程,并画出大致图象; ②证明:设“外心”坐标为M(m,n),则 由|MA|=|MC|,得|m-1|+|n-3|=|m-1|+|n-9|,所以点M在y=6上; 又因为|MB|=|MC|,即|m-1|+|n-9|=|m-6|+|n-9|,所以点M在x=
7
2
上; ∴M(
7
2
,6); ∴△ABC三边的“垂直平分线”交于一点M,且M(
7
2
,6). 【解析】
(1))利用“圆”的概念,能够求出“圆周”上的所有点到点Q(a,b)的“距离”均为 r的“圆”的方程; (2)①由已知条件,得|x-1|+|y-3|=|x-6|+|y-9,由此能够求出线段AB的垂直平分线的轨迹方程并画出大致图象; ②设三角形“外心”坐标为M(m,n),由|MA|=|MB|=|MC|结合绝对值的性质,求得点M的坐标. 本题考查了新定义的应用问题,解题时要认真审题,仔细解答,注意合理地进行等价转化,是难题.
同课章节目录
