2018-2019学年上海市杨浦区高二(上)期中数学试卷(解析版)
文档属性
| 名称 | 2018-2019学年上海市杨浦区高二(上)期中数学试卷(解析版) |  | |
| 格式 | zip | ||
| 文件大小 | 187.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-01-17 19:15:59 | ||
图片预览



文档简介
2018-2019学年上海市杨浦区高二(上)期中数学试卷
一、选择题(本大题共4小题,共12.0分)
无穷等比数列9、-3、1,-
1
3
、……,各项的和为( )
A. ?
27
4
B.
27
4
C. 27 D. ?
1
9
在△ABC中,AD为BC边上的中线,E为△ABC的重心,则
????
=( )
A.
1
3
????
+
1
3
????
B.
2
3
????
+
2
3
????
C.
1
2
????
+
1
2
????
D.
1
4
????
+
1
4
????
已知直角坐标系xOy平面上的直线
??
??
+
??
??
=1经过第一、第二和第四象限,则a,b满足( )
A. ??>0,??>0 B. ??>0,??<0 C. ??<0,??>0 D. ??<0,??<0
已知
??
,
??
,
??
是平面向量,
??
是单位向量.若非零向量
??
与
??
的夹角为
??
3
,向量
??
满足
??
2
-4
??
?
??
+3=0,则|
??
-
??
|的最小值是( )
A.
3
?1 B.
3
+1 C. 2 D. 2?
3
二、填空题(本大题共10小题,共30.0分)
求值:
??→∞
??????
5??+2
3??+2
=______.
已知向量
??
=(k,1)与
??
=(2,k+1)平行,则实数k=______.
已知点M(0.b)与点N(-
3
,1)连成直线的倾斜角为120°,则b=______.
已知|
??
|=1,|
??
|=2,向量
??
与
??
的夹角为60°,则|
??
+
??
|=______.
直线l1:x-y+1=0与直线l2:x-y+5=0之间的距离是______.
已知
??
=(2,-1),
??
=(3,4),则
??
在
??
的方向上的投影为______.
过点A(1,6)且与直线
??+1
7
=
??+2
5
垂直的直线的点法向式方程为______.
已知A(-1,4)、B(3,2),如果点H是线段AB的两个三等分点中距离A较近的那个三等分点,则点H的坐标是______.
直线y=k(x+3)-2与直线y=-
1
4
x+1的交点在第一象限,则斜率k的取值范围是______.
如图,在平面四边形ABCD中,AB⊥BC,AD⊥CD,∠BAD=120°,AB=AD=1.若点E为边CD上的动点,当
????
?
????
取到最小值时,DE的长为______.
三、解答题(本大题共5小题,共58.0分)
设{an}是首项为1,公比为q(q>0)的等比数列,前n项和为Sn,求
??→∞
??????
??
??
??
??+1
值.
已知向量
??
=(
3
,1),
??
=(0,1). (1)(
??
+k
??
)⊥(
??
-k
??
),求实数k的值; (2)向量2k
??
+7
??
与向量
??
+k
??
的夹角大于90°,求实数k的取值范围.
已知直线l的方程为3x+4y-12=0,分别求满足下列条件的直线l′的一般式方程. (1)过点(1,2)且与l的夹角为45°; (2)l'为l绕原点逆时针旋转90°后得到的直线.
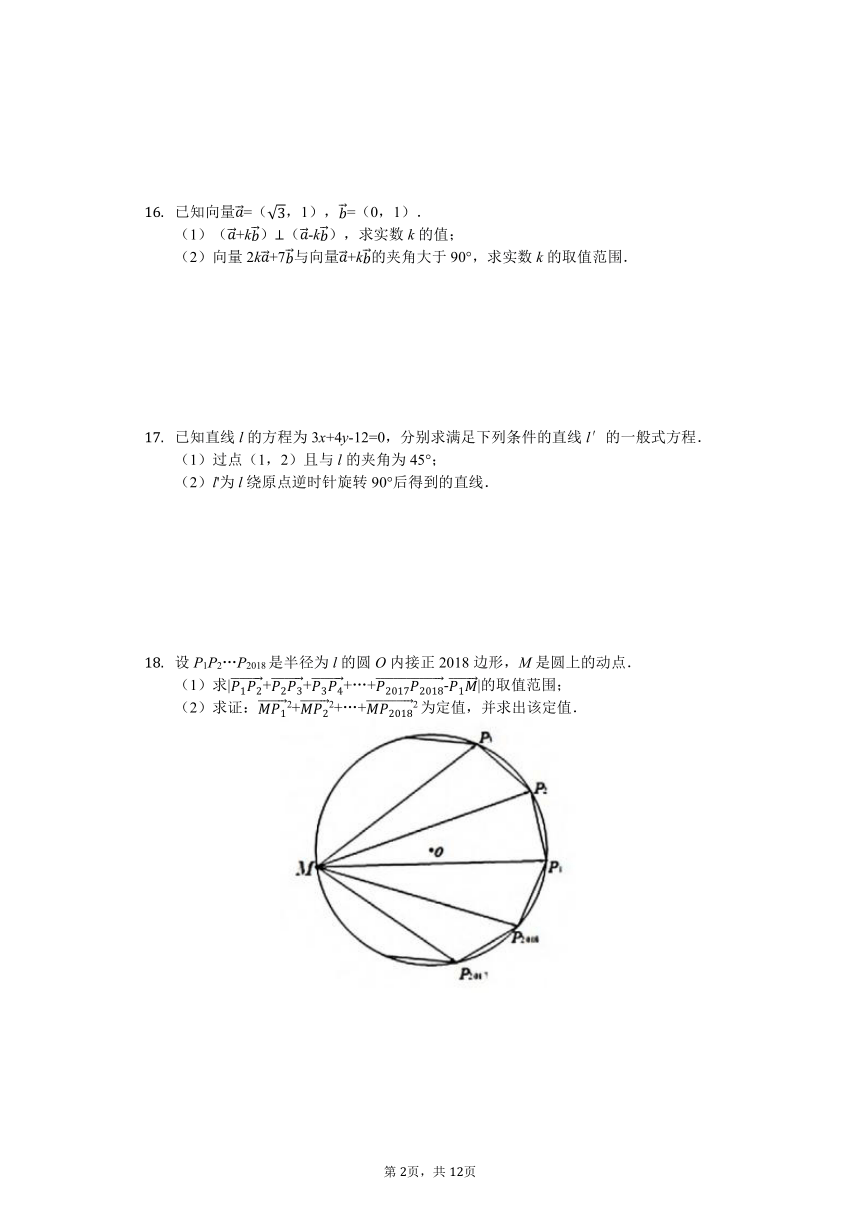
设P1P2…P2018是半径为l的圆O内接正2018边形,M是圆上的动点. (1)求|
??
1
??
2
+
??
2
??
3
+
??
3
??
4
+…+
??
2017
??
2018
-
??
1
??
|的取值范围; (2)求证:
??
??
1
2+
??
??
2
2+…+
??
??
2018
2为定值,并求出该定值.
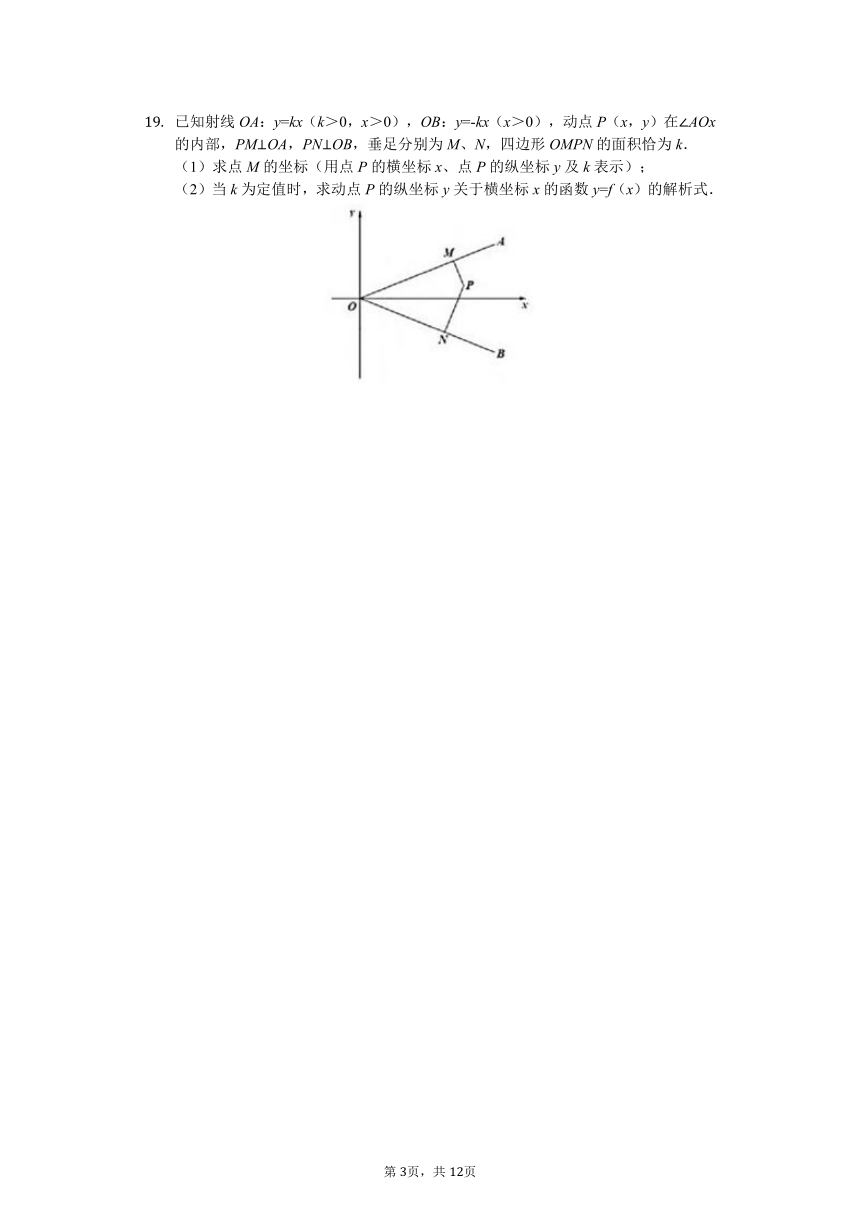
已知射线OA:y=kx(k>0,x>0),OB:y=-kx(x>0),动点P(x,y)在∠AOx的内部,PM⊥OA,PN⊥OB,垂足分别为M、N,四边形OMPN的面积恰为k. (1)求点M的坐标(用点P的横坐标x、点P的纵坐标y及k表示); (2)当k为定值时,求动点P的纵坐标y关于横坐标x的函数y=f(x)的解析式.
答案和解析
1.【答案】B 【解析】
解:等比数列9、-3、1,-、……,可得公比为, 前n项和为:. 无穷等比数列9、-3、1,-、……,各项的和为:==. 故选:B. 求出等比数列的前n项和,然后求解极限即可. 本题考查数列求和以及数列的极限的运算.是基本知识的考查.
2.【答案】A 【解析】
解:因为E为△ABC的重心,所以==?(+)=+, 故选:A. 根据重心的性质以及平行四边形法则可得. 本题考查了重心的性质以及向量的平行四边形法则.属基础题.
3.【答案】A 【解析】
解:坐标系xOy平面上的直线+=1经过第一、第二和第四象限,如图所示; 则a>0,b>0. 故选:A. 根据题意画出图形,结合图形知a>0且b>0. 本题考查了直线方程的应用问题,是基础题.
4.【答案】A 【解析】
解:由-4?+3=0,得, ∴()⊥(), 如图,不妨设, 则的终点在以(2,0)为圆心,以1为半径的圆周上, 又非零向量与的夹角为,则的终点在不含端点O的两条射线y=(x>0)上. 不妨以y=为例,则|-|的最小值是(2,0)到直线的距离减1. 即. 故选:A. 把等式-4?+3=0变形,可得得,即()⊥(),设,则的终点在以(2,0)为圆心,以1为半径的圆周上,再由已知得到的终点在不含端点O的两条射线y=(x>0)上,画出图形,数形结合得答案. 本题考查平面向量的数量积运算,考查数学转化思想方法与数形结合的解题思想方法,属难题.
5.【答案】
5
3
【解析】
解:===. 故答案为:. 直接利用数列的极限的运算法则化简求解即可. 本题考查数列的极限的运算法则的应用,考查计算能力.
6.【答案】-2或1 【解析】
解:∵与平行; ∴k?(k+1)-2=0; 解得k=-2或1. 故答案为:-2或1. 根据即可得出k?(k+1)-2=0,解出k即可. 考查向量坐标的概念,平行向量的坐标关系.
7.【答案】-2 【解析】
解:k==tan120°, 解得b=-2, 故答案为:-2. 由题意可得k==tan120°,解得即可 本题考查了斜率公式,以及倾斜角和斜率的关系,属于基础题
8.【答案】
7
【解析】
解:由题意可得=||?||?cos60°=1×2×=1, ∴|+|====, 故答案为:. 由题意可得=1,再根据|+|=,计算求得结果. 本题主要考查两个向量的数量积的定义,求向量的模的方法,属于基础题.
9.【答案】2
2
【解析】
解:直线l1:x-y+1=0与直线l2:x-y+5=0之间的距离==2. 故答案为:2. 利用平行线之间的距离公式即可得出. 本题考查了平行线之间的距离公式,考查了推理能力与计算能力,属于基础题.
10.【答案】
2
5
【解析】
解:由题意得: 在的方向上的投影为:==, 故答案为:. 根据投影的几何意义求出即可. 本题考查了向量的投影,考查向量的坐标运算,是一道基础题.
11.【答案】7(x-1)+5(y-6)=0 【解析】
解:与直线=垂直的直线的法向量为(7,5), 则点法向式直线方程为7(x-1)+5(y-6)=0. 故答案为:7(x-1)+5(y-6)=0. 根据向量垂直的条件得点法向式直线方程. 本题考查了直线点法向式方程,属于基础题
12.【答案】(
1
3
,
10
3
) 【解析】
解:设H(x,y); ∵点H是线段AB的两个三等分点中距离A较近的那个三等分点; ∴根据定比分点公式得:; ∴; ∴H(). 故答案为:. 可设H(x,y),根据条件及定比分点公式可得出,这样即可得出点H的坐标. 考查三等分点的定义,以及线段的定比分点公式.
13.【答案】(
2
7
,1) 【解析】
解:联立,解之可得交点(,), 由题意可得,, 解之可得<k<1,故k的取值范围是(,1) 故答案为:(,1) 联立方程求出两直线的交点坐标,根据交点在第一象限这一条件来确定k的取值范围即可. 本题考查两直线的交点问题,涉及二元一次方程组和不等式的解法,属中档题.
14.【答案】
3
4
【解析】
解:设DE=x, ∵∠BAD=120°,AB=AD=1, △ABD中,由余弦定理可得, BD2=AB2+AD2-2AB?ADcos120°=1+1=3, ∴, △ABD中,∠ABD=∠BDA=30°, ∵AB⊥BC,AD⊥CD, ∴∴=()?() = =1×1×cos60°+1+0+1×x×cos150°+0+x2 = =,此时DE=x=, 故答案为:. 设DE=x,由已知结合余弦定理可求∠ABD=∠BDA=30°,而=()?(),展开结合向量的数量积的运算及二次函数的性质可求. 本题以向量的基本运算为载体,主要考查了向量的数量积的定义的应用及二次函数的最值的求解,属于知识的简单综合.
15.【答案】解:当公比q满足0<q<1时, Sn=1+q+q2+…+qn-1=
1?
??
??
1???
,于是
??
??
??
??+1
=
1?
??
??
1?
??
??+1
,
??→∞
??????
??
??
??
??+1
=1. 当公比q=1时,Sn=1+1+…+1=n,于是
??
??
??
??+1
=
??
??+1
. 因此
??→∞
??????
??
??
??
??+1
=
??→∞
??????
??
??+1
═1 当公比q>1时,Sn=1+q+q2+…+qn-1=
??
??
?1
???1
于是
??
??
??
??+1
=
??
??
?1
??
??+1
?1
. 因此?
??→∞
??????
??
??
??
??+1
=
??→∞
??????
??
??
?1
??
??+1
?1
=
??→∞
??????
1?
1
??
??
???
1
??
??
=
1
??
. 综合以上讨论得到
??→∞
??????
??
??
??
??+1
=
1,0<??≤1
1
??
,??>1
. 【解析】
当公比q满足0<q<1时,Sn=,求出的值,然后求解极限,当公比q=1时,Sn=n,求出的值.当公比q>1时,求出的值.综合然后求解极限的值即可. 本题考查等比数列的极限,解题时要分情况进行讨论,考虑问题要全面,避免丢解.
16.【答案】解:(1)
??
2
=4,
??
2
=1; ∵(
??
+??
??
)⊥(
??
???
??
); ∴(
??
+??
??
)?(
??
???
??
)=
??
2
?
??
2
??
2
=4-k2=0; ∴k=±2; (2)∵向量2k
??
+7
??
与向量
??
+k
??
的夹角大于90°; ∴(2??
??
+7
??
)?(
??
+??
??
)=2??
??
2
+(2
??
2
+7)
??
?
??
+7??
??
2
=2k2+15k+7<0; 解得?7<??<?
1
2
; ∴实数k的取值范围为(?7,?
1
2
). 【解析】
(1)可求出,根据即可得出,从而求出k的值; (2)根据向量2k+7与向量+k的夹角大于90°即可得出,进行数量积的运算即可求出k的取值范围. 考查向量垂直的充要条件,向量数量积的运算及计算公式.
17.【答案】解:(1)直线l的方程为3x+4y-12=0,则l的斜率为-
3
4
, 设所求直线的斜率为k,则
???(?
3
4
)
1+(?
3
4
)??
=±tn45°=±1, ∴
??+
3
4
1?
3
4
??
=±1, 解得k=-7或k=
1
7
, ∴k=-7时,直线方程为y-2=-7(x-1),化为一般式方程是7x+y-9=0; ∴k=
1
7
时,直线方程为y-2=
1
7
(x-1),化为一般式方程是x-7y+13=0; 综上知,所求的直线方程为7x+y-9=0或x-7y+13=0; (2)直线3x+4y-12=0与坐标轴的交点坐标为(4,0)和(0,3), 则旋转后的直线与坐标轴的交点坐标为(-3,0)和(0,4), ∴所求的直线方程为
??
?3
+
??
4
=1,即为4x-3y+12=0. 【解析】
(1)求出直线l的斜率,设所求直线的斜率为k,利用两条直线所成的角求出k的值,再写出所求的直线方程; (2)根据直线3x+4y-12=0与坐标轴的交点求出旋转后的直线与坐标轴的交点坐标,即可写出所求的直线方程. 本题考查了直线方程与应用问题,也考查了两条直线所成的角以及直线旋转问题,是中档题.
18.【答案】解:(1)∵P1P2…P2018是半径为l的圆O内接正2018边形,M是圆上的动点. ∴|
??
1
??
2
+
??
2
??
3
+
??
3
??
4
+…+
??
2017
??
2018
-
??
1
??
| =|
??
1
??
2018
-
??
1
??
| =|
??
??
2018
|, ∴|
??
1
??
2
+
??
2
??
3
+
??
3
??
4
+…+
??
2017
??
2018
-
??
1
??
|的取值范围是[0,2]. 证明:(2)把
??
??
1
,
??
??
2
,…,
??
??
2018
这2018个向量都旋转
2??
2018
后,
??
??
1
+
??
??
2
+…+
??
??
2018
不变, ∴和向量旋转
2??
2018
弧度后也不变, ∴
??
??
1
+
??
??
2
+…+
??
??
2018
=
0
, ∴
??
??
1
2+
??
??
2
2+…+
??
??
2018
2 =(
??
??
1
?
????
)2+(
??
??
2
-
????
)2+…+(
??
??
2018
-
????
)2 =(
??
??
1
2
+
??
??
2
2
+…+
??
??
218
2
)-2
????
?(
??
??
1
+
??
??
2
+…+
??
??
2018
)+2018
????
2 =2018-2
????
?(
??
??
1
+
??
??
2
+…+
??
??
2018
)+2018 =2018-2
????
?
0
+2018 =4036. 【解析】
(1)推导出|+++…+-|=|-|=||,由此能求出|+++…+-|的取值范围. (2)推导出+…+=,从而2+2+…+2=()2+(-)2+…+(-)2=(+…+)-2?()+20182,由此能证明2+2+…+2为定值,并能求出该定值. 本题考查向量和的模的取值范围的求法,考查向量的平方和为定值的证明,考查向量加法法则等基础知识,考查运算求解能力,考查函数与方程思想,是中档题.
19.【答案】解:(1)设M(xM,yM),则
??
??
=??
??
??
??
??
???=?
1
??
(
??
??
???)
,解得xM=
??+????
1+
??
2
,yM=
??(??+????)
1+
??
2
, 故M的坐标为(
??+????
1+
??
2
,
??(??+????)
1+
??
2
), (2)OM=
1+
??
2
?(
??+????
1+
??
2
),点P到直线OA的距离为
|???????|
1+
??
2
, 根据点P的位置可知PM=
???????
1+
??
2
, 因此S△OMP=
1
2
OM?PM=
1
2
?
(??+????)(???????)
1+
??
2
, 同理,把k替换为-k可知N(
???????
1+
??
2
,-
??(???????)
1+
??
2
), ON=
1+
??
2
?(
???????
1+
??
2
),PN=
????+??
1+
??
2
, 因此S△ONP=
1
2
ON?PN=
1
2
?
(???????)(????+??)
1+
??
2
, ∴四边形OMPN的面积S=S△OMP+S△ONP=
1
2
?
(??+????)(???????)
1+
??
2
+
1
2
?
(???????)(????+??)
1+
??
2
=
??
1+
??
2
(x2-y2), 因此
??
1+
??
2
(x2-y2)=k, 解得y=
??
2
?1?
??
2
, 注定义域这里不作要求, 由x>0,0<y<kx,0<y<
1
??
x可得: 当0<k<1时,x∈(
??
2
+1
,
??
2
+1
1?
??
2
), 当k=1时,x∈(
2
,+∞), 当k>1时,x∈(
??
2
+1
,k
??
2
+1
??
2
?1
) 【解析】
(1)设M(xM,yM),则,解的即可 (2)先要仔细分析题目所给的条件,设出点M、N的坐标,将四边形分解成两个三角形:三角形OMP、三角形ONP分别表示出面积,然后求和即可找到x、y之间的关系式,进而即可获得问题的解答 本题考查的是函数解析式的求解问题.在解答的过程当中充分体现了图形分割的思想、分类讨论的思想以及问题转化的思想.值得同学们体会和反思.
同课章节目录
