华师大九年级下《第26章二次函数》单元检测试卷(含答案解析)
文档属性
| 名称 | 华师大九年级下《第26章二次函数》单元检测试卷(含答案解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 184.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-01-17 00:00:00 | ||
图片预览



文档简介
华师大版九年级数学下册 第26章 二次函数 单元检测试卷
一、单选题(共10题;共30分)
1.将二次函数??=
??
2
?4???1化为??=
????
2
+??的形式,结果为(????? )
A.???=
??+2
2
+5????????????/B.???=
??+2
2
?5????????????/C.???=
???2
2
+5????????????/D.???=
???2
2
?5
2.把抛物线 ??=
??
2
向右平移1个单位,再向上平移3个单位,得到抛物线的解析式为(?? )
A.???=
(???1)
2
+3??????????????/B.???=
(??+1)
2
?3??????????????/C.???=
(???1)
2
?3??????????????/D.???=
(??+1)
2
+3
3.函数y=(x+1)2-2的最小值是( ??)
A.?1 ????????????????????????????????????/B.?-1 ????????????????????????????????????/C.?2 ????????????????????????????????????/D.?-2
4.如图,抛物线y=ax2+bx+c(a>0)过点(1,0)和点(0,-2),且顶点在第三象限,设P=a-b+c,则P的取值范围是( ??)
/
A.?-1<P<0??????????????????????????/B.?-2<P<0??????????????????????????/C.?-4<P<-2??????????????????????????/D.?-4<P<0
5.
抛物线y=-(x+2)2-3的顶点坐标是?? (? ?? )
A.?(-2,3)??????????????????????/B.?(2,3)??????????????????????/C.?(-2,-3)??????????????????????/D.?(2,-3)
6.把抛物线y=ax2+bx+c的图象向右平移3个单位,再向下平移2个单位,所得图象的解析式为y=x2-2x+3,则b+c的值为(????)
A.?9?????????????????????????????????????????/B.?12?????????????????????????????????????????/C.?-14?????????????????????????????????????????/D.?10
7.在下列函数关系式中,y是x的二次函数的是( )
A.?
??
??
=6?????????????????????????????B.?????=?6?????????????????????????????C.???+
??
2
=6?????????????????????????????D.???=?6??
8.下列关系中,是二次函数关系的是( ? ?)
A.?当距离S一定时,汽车行驶的时间t与速度v之间的关系。 B.?在弹性限度时,弹簧的长度y与所挂物体的质量x之间的关系。 C.?圆的面积S与圆的半径r之间的关系。 D.?正方形的周长C与边长a之间的关系。
9.抛物线y=ax2+bx+c的图角如图,则下列结论:①abc>0;②a+b+c=2;③a>
1
2
?;④b<1. 其中正确的结论是( ) /
A.?①②?????????????????????????????????????B.?②③?????????????????????????????????????C.?②④?????????????????????????????????????D.?③④
10.二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论: ①2a+b=0; ②a+c>b;③抛物线与x轴的另一个交点为(3,0);④abc>0. 其中正确的结论的个数是(?? ) /
A.?1个???????????????????????????????????????B.?2个???????????????????????????????????????C.?3个???????????????????????????????????????D.?4个
二、填空题(共10题;共30分)
11.二次函数y=x2+4x+5中,当x=________时,y有最小值.
12.若将二次函数y=x2-2x+3配方为y=(x-h)2 +k的形式,则y=________.
13.已知抛物线 ??=2
??
2
?????+3 的对称轴是直线 ??=1 ,则 ?? 的值为________.
14.将函数 ??=?
??
2
所在的坐标系先向左平移 2 个单位再向下平移 3 个单位,则函数在新坐标系中的函数关系式是________.
15.把抛物线y=x2 向右平移3个单位,再向下平移1个单位,则得到抛物线________.
16.如图.已知二次函数y1=ax2+bx+c与一次函数y2=kx+m的图象相交于点A(﹣2,4),B(8,2),根据图象能使y1>y2成立的x取值范围是________. /
17.张力同学在校运动会上投掷标枪,标枪运行的高度h(m)与水平距离x(m)的关系式为h=﹣
1
48
x2+
46
48
x+2,则大力同学投掷标枪的成绩是________m.
18.已知点 ?? ? (?3,??) 和点 ?? ? (1,??) 是抛物线 ??=2
??
2
+????+3 图象上的两点,则 ?? =________.
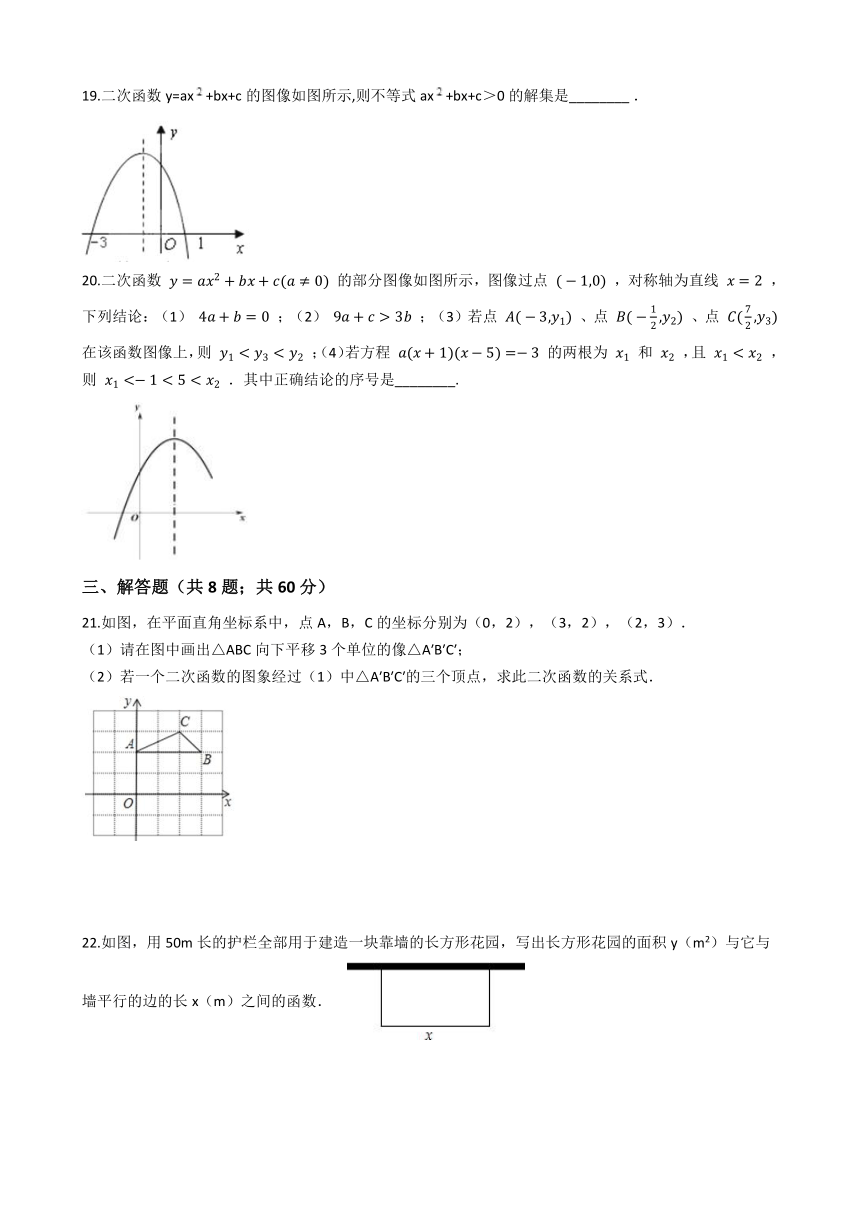
19.二次函数y=ax/+bx+c的图像如图所示,则不等式ax/+bx+c>0的解集是________?. /
20.二次函数 ??=??
??
2
+????+??(??≠0) 的部分图像如图所示,图像过点 (?1,0) ,对称轴为直线 ??=2 ,下列结论:(1) 4??+??=0 ;(2) 9??+??>3?? ;(3)若点 ??(?3,
??
1
) 、点 ??(?
1
2
,
??
2
) 、点 ??(
7
2
,
??
3
) 在该函数图像上,则
??
1
<
??
3
<
??
2
;(4)若方程 ??(??+1)(???5)=?3 的两根为
??
1
和
??
2
,且
??
1
<
??
2
,则
??
1
??
2
.其中正确结论的序号是________. /
三、解答题(共8题;共60分)
21.如图,在平面直角坐标系中,点A,B,C的坐标分别为(0,2),(3,2),(2,3). (1)请在图中画出△ABC向下平移3个单位的像△A′B′C′; (2)若一个二次函数的图象经过(1)中△A′B′C′的三个顶点,求此二次函数的关系式. /
22.如图,用50m长的护栏全部用于建造一块靠墙的长方形花园,写出长方形花园的面积y(m2)与它与墙平行的边的长x(m)之间的函数. /
23.已知抛物线y=x2+(m+4)x-2(m+6)(m是常数,m≠-8)与x轴有两个不同的交点A、B,点A、点B关于直线x=1对称,抛物线的顶点为C. (1)此抛物线的解析式; (2)求点A、B、C的坐标.
24.向上抛掷一个小球,小球在运行过程中,离地面的距离为y(m),运行时间为x(s),y与x之间存在的关系为y=-
1
2
x2+3x+2.问:小球能达到的最大高度是多少?
25.(1)已知y=(m2+m)
??
??
2
?2???1
+(m﹣3)x+m2是x的二次函数,求出它的解析式. (2)用配方法求二次函数y=﹣x2+5x﹣7的顶点坐标并求出函数的最大值或最小值.
26.永嘉某商店试销一种新型节能灯,每盏节能灯进价为18元,试销过程中发现,每周销量y(盏)与销售单价x(元)之间关系可以近似地看作一次函数y=﹣2x+100.(利润=售价﹣进价) (1)写出每周的利润w(元)与销售单价x(元)之间函数解析式;
(2)当销售单价定为多少元时,这种节能灯每周能够获得最大利润?最大利润是多少元? (3)物价部门规定,这种节能灯的销售单价不得高于30元.若商店想要这种节能灯每周获得350元的利润,则销售单价应定为多少元?
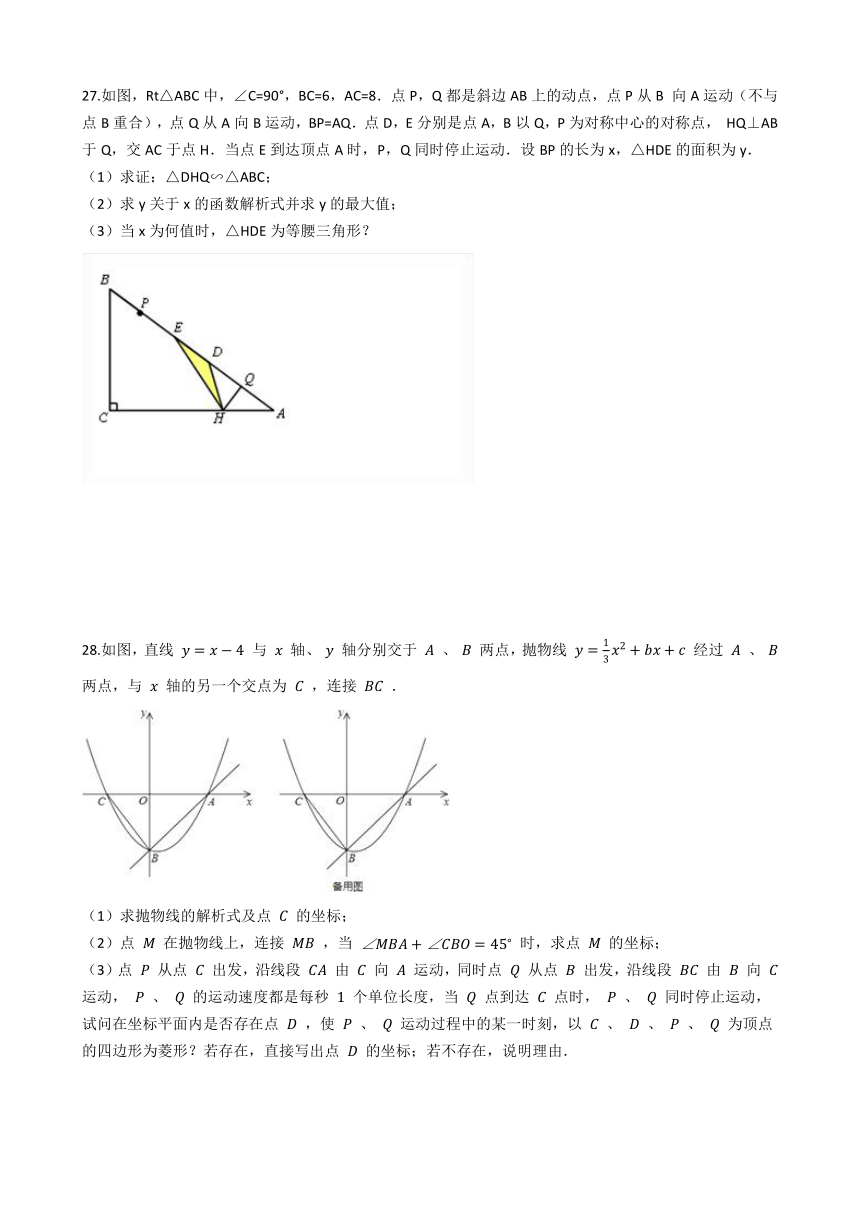
27.如图,Rt△ABC中,∠C=90°,BC=6,AC=8.点P,Q都是斜边AB上的动点,点P从B 向A运动(不与点B重合),点Q从A向B运动,BP=AQ.点D,E分别是点A,B以Q,P为对称中心的对称点, HQ⊥AB于Q,交AC于点H.当点E到达顶点A时,P,Q同时停止运动.设BP的长为x,△HDE的面积为y. (1)求证:△DHQ∽△ABC; (2)求y关于x的函数解析式并求y的最大值; (3)当x为何值时,△HDE为等腰三角形? /
28.如图,直线 ??=???4 与 ?? 轴、 ?? 轴分别交于 ?? 、 ?? 两点,抛物线 ??=
1
3
??
2
+????+?? 经过 ?? 、 ?? 两点,与 ?? 轴的另一个交点为 ?? ,连接 ???? .
/
(1)求抛物线的解析式及点 ?? 的坐标;
(2)点 ?? 在抛物线上,连接 ???? ,当 ∠??????+∠??????=
45
°
时,求点 ?? 的坐标;
(3)点 ?? 从点 ?? 出发,沿线段 ???? 由 ?? 向 ?? 运动,同时点 ?? 从点 ?? 出发,沿线段 ???? 由 ?? 向 ?? 运动, ?? 、 ?? 的运动速度都是每秒 1 个单位长度,当 ?? 点到达 ?? 点时, ?? 、 ?? 同时停止运动,试问在坐标平面内是否存在点 ?? ,使 ?? 、 ?? 运动过程中的某一时刻,以 ?? 、 ?? 、 ?? 、 ?? 为顶点的四边形为菱形?若存在,直接写出点 ?? 的坐标;若不存在,说明理由.
答案解析部分
一、单选题
1.【答案】D
【考点】二次函数的三种形式
【解析】【分析】??=
??
2
?4???1=
???2
2
?5. 故选D.
2.【答案】D
【考点】二次函数图象的几何变换
【解析】【解答】 抛物线 ??=
??
2
先向右平移1个单位所得抛物线的解析式为 ??=
(???1)
2
, 抛物线 ??=
(???1)
2
再向上平移3个单位所得抛物线的解析式为 ??=
(???1)
2
+3 , 故答案为:D. 【分析】根据函数图象平移的法则即可得到结果.
3.【答案】D
【考点】二次函数的最值
【解析】【分析】此函数的最小值,在x=-1时,y=-2,此时取最小值。 故选D. 【点评】二次函数的解析式有三种形式:(1)一般式:y=ax2+bx+c(a≠0,a、b、c为常数);(2)顶点式:y=a(x-h)2+k;(3)交点式(与x轴):y=a(x-x1)(x-x2).
4.【答案】D
【考点】二次函数图象与系数的关系,二次函数图象上点的坐标特征
【解析】【解答】解:∵二次函数的图象开口向上,∴a>0
∵对称轴在y轴的左边,∴ ?
??
2??
<0。∴b>0
∵图象与y轴的交点坐标是(0,﹣2),过(1,0)点,代入得:a+b﹣2=0
∴a=2﹣b,b=2﹣a;
∴y=ax2+(2﹣a)x﹣2
把x=﹣1代入得:y=a﹣(2﹣a)﹣2=2a﹣4,
∵b>0,∴b=2﹣a>0
∴a<2
∵a>0,∴0<a<2
∴0<2a<4
∴﹣4<2a﹣4<0,即﹣4<P<0.
故答案为:D.
【分析】将(0,﹣2),(1,0)代入二次函数可得c=-2,a+b﹣2=0,可将b=2﹣a代入(或将a=2-b代入)P=a-b+c=2a-4,则可得P是关于a的一次函数,要求P的取值范围,则需要求a取值范围;观察二次函数的图象可得a>0,且?
??
2??
<0,则b<0,即2-a<0,求出a的取值范围后再求P的范围。
5.【答案】A
【考点】二次函数的三种形式
【解析】【分析】已知解析式为顶点式,可直接根据顶点式的坐标特点,求顶点坐标,从而得出对称轴. 【解答】y=-(x+2)2-3是抛物线的顶点式, 根据顶点式的坐标特点可知,顶点坐标为(-2,-3). 故答案为C. 【点评】此题主要考查了二次函数的性质,关键是熟记:顶点式y=a(x-h)2+k,顶点坐标是(h,k),对称轴是x=h.
6.【答案】B
【考点】二次函数图象与几何变换
【解析】【分析】先化解析式y=x2-2x+3为顶点式,再根据二次函数的平移规律求解即可. y=x2-2x+3=(x-1)2+2 则把抛物线y=(x-1)2+2的图象向左平移3个单位,再向上平移2个单位后的解析式为 y=(x+2)2+4=x2+4x+8 所以b=4,c=8,b+c=12 故选B.
7.【答案】C
【考点】二次函数的定义
【解析】【解答】A、
??
??
=6,可化为y=
1
6
x的形式,不符合二次函数的一般形式,故本选项错误;B、xy=﹣6符合反比例函数的一般形式,不符合二次函数的一般形式,故本选项错误;C、y+x2=6可化为y=-x2+6,符合二次函数的一般形式,故本选项正确;D、y=﹣6x符合正比例函数的一般形式,不符合二次函数的一般形式,故本选项错误.故选C. 【分析】根据二次函数的定义对四个选项进行逐一分析即可,即一般地,形如y=ax2+bx+c(a、b、c是常数,a≠0)的函数,叫做二次函数.
8.【答案】C
【考点】二次函数的定义
【解析】【解答】由题意,A的解析式为 /,B的解析式为 /,C的解析式为 /,D的解析式为 /,唯有B是二次函数关系,故选C. 【分析】能够运用实际问题的意义列出正确的解析式,并进行分析判断是否是二次函数,要根据二次函数的定义的基本要求.
9.【答案】B
【考点】二次函数图象与系数的关系,二次函数图象上点的坐标特征
【解析】
【分析】由图象可知a>0,b>0,c<0;再由特殊点可以判定对错.
【解答】由图象可知a>0,b>0,c<0,∴abc<0;故①错误; 由(1,2)代入抛物线方程可得a+b+c=2;故②正确; 当x=-1时y<0,即a-b+c<0(1), 由②a+b+c=2可得:c=2-a-b(2), 把(2)式代入(1)式中得:b>1;故④错误; ∵对称轴公式-
??
2??
>-1, ∴2a>b, ∵b>1, ∴2a>1,即a>
1
2
;故③正确. 故选B.
10.【答案】B
【考点】二次函数图象与系数的关系
【解析】【解答】解:∵抛物线的对称轴为直线x=﹣
??
2??
?=1, ∴b=﹣2a,即2a+b=0,所以①正确; ∵x=﹣1时,y<0, ∴a﹣b+c<0,即a+c<b,所以②错误; ∵点(﹣2,0)关于直线x=1的对称点为(4,0), ∴抛物线与x轴的另一个交点为(4,0),所以③错误; ∵抛物线开口向上, ∴a>0, ∴b=﹣2a<0, ∵抛物线与y轴的交点在x轴下方, ∴c<0, ∴abc>0,所以④正确. 故选B. 【分析】利用抛物线的对称轴为直线x=﹣
??
2??
?=1,则可对①进行判断;利用x=﹣1时,函数值为负数可对②进行判断;通过求出点(﹣2,0)关于直线x=1的对称点为(4,0)可对③进行判断;由抛物线开口向上得到a>0,则b=﹣2a<0,再由抛物线与y轴的交点在x轴下方得到c<0,则可对④进行判断.
二、填空题
11.【答案】﹣2
【考点】二次函数的最值
【解析】【解答】解:∵二次函数y=x2+4x+5可化为y=(x+2)2+1, ∴当x=﹣2时,二次函数y=x2+4x+5有最小值. 故答案为:﹣2. 【分析】先用配方法把函数化为顶点式的形式,再根据其解析式即可求解.
12.【答案】??=
(???1)
2
+2
【考点】二次函数y=ax^2+bx+c与二次函数y=a(x-h)^2+k的转化
【解析】【解答】y=
??
2
?2??+3 ?=(
??
2
?2??+1 )+2= (???1
)
2
+2.故答案为 ??=
(???1)
2
+2 .
【分析】将二次函数的一般式配方成顶点式。
13.【答案】b=4
【考点】二次函数y=ax^2+bx+c的性质
【解析】【解答】由抛物线的对称轴x=-
??
2??
和已知条件抛物线y=2
??
2
-bx+3的对称轴是直线x=1,得到的等式,即可求出b的值.
【分析】根据抛物线的对称轴直线公式建立方程,求解即可求出b的值。
14.【答案】??=?
(???2)
2
+3
【考点】二次函数图象的几何变换
【解析】【解答】坐标系移动,等同于函数向相反的方向移动,则可得移动后函数为: ??=?
(???2)
2
+3 , 故答案为: ??=?
(???2)
2
+3 . 【分析】根据二次函数图像的平移规律:上加下减,左加右减,将抛物线y=ax2向上或向下平移m个单位,再向左或向右平移n个单位即得到y=a(x±n)2±m。根据平移规则即可得出平移后的抛物线的解析式。
15.【答案】y=(x﹣3)2﹣1
【考点】二次函数图象与几何变换
【解析】【解答】解:抛物线y=x2向右平移3个单位,得:y=(x﹣3)2; 再向下平移1个单位,得:y=(x﹣3)2﹣1. 故答案是:y=(x﹣3)2﹣1. 【分析】根据二次函数图象左加右减,上加下减的平移规律进行解答即可.
16.【答案】x<﹣2或x>8
【考点】二次函数与不等式(组)
【解析】【解答】解:∵A(﹣2,4)、B(8,2), ∴不等式ax2+bx+c>kx+m成立的x的取值范围是x<﹣2或x>8. 故答案为x<﹣2或x>8. 【分析】根据函数图象写出抛物线在直线上方部分的x的取值范围即可
17.【答案】48
【考点】因式分解法解一元二次方程,二次函数图像与坐标轴的交点问题
【解析】【解答】解:∵h=﹣
1
48
x2+
46
48
x+2, ∴当h=0时,0=﹣
1
48
x2+
46
48
x+2, 解得,x1=﹣2,x2=48, 即大力同学投掷标枪的成绩是48m, 故答案为:48. 【分析】先根据h=0时,建立关于x的方程求解,即可得出答案。
18.【答案】b=4
【考点】二次函数图象与系数的关系
【解析】【解答】把A(-3,m)和点B(1,m)代入y=2x2+bx+3得: {
??=2×9?3??+3
??=2+??+3
,解得:b=6
【分析】把点A和点B的坐标代入抛物线的解析式,求出b的值.
19.【答案】﹣3<x<1
【考点】二次函数的图象,抛物线与x轴的交点,二次函数与不等式(组)
【解析】【解答】由图可知,一元二次不等式ax2+bx+c>0的解是﹣3<x<1. 故答案是﹣3<x<1. 【分析】考查二次函数与不等式(组).
20.【答案】(1)(4)
【考点】二次函数图象与系数的关系
【解析】【解答】:∵抛物线的对称轴为直线x=-
??
2??
=2,∴b=-4a>0,即4a+b=0,所以(1)正确;∵x=-3时,y<0,∴9a-3b+c<0,即9a+c<3b,所以(2)错误;∵抛物线的对称轴为直线x=-
??
2??
=2,图象与x轴交于(-1,0), ∴抛物线x轴的另一个交点是(5,0),∵点A(-3,y1)、点B(-
1
2
,y2)、点C(
7
2
,y3),∵
7
2
-2=
3
2
,2-(-
1
2
)=
5
2
,∴
3
2
<
5
2
∴点C离对称轴的距离近,∴y3>y2 , ∵a<0,-3<-
1
2
<2,∴y1<y2∴y1<y2<y3 , 故(3)错误.如图, / ∵a<0,∴(x+1)(x-5)=-3/a>0,即(x+1)(x-5)>0,故x<-1或x>5,故(4)正确. 【分析】由抛物线的对称轴直线,得到4a+b=0,图象与x轴交于(-1,0),得到抛物线x轴的另一个交点,由已知得到点C离对称轴的距离近,得到y3>y2 , 由a<0,得到y1<y2<y3.
三、解答题
21.【答案】(1)如图: / (2)由题意得A′,B′,C′的坐标分别是(0,﹣1),(3,﹣1),(2,0), 设过点A′、B′、C′的二次函数的关系式为y=ax2+bx+c, 则有
??=?1
9??+3??+??=?1
4??+2??+??=0
, 解得??=?
1
2
,??=
3
2
,??=?1, ∴二次函数的关系式为??=?
1
2
??
2
+
3
2
???1.
【考点】待定系数法求二次函数解析式
【解析】【分析】(1)直接作出图形即可,(2)根据题意写出A′,B′,C′的坐标,设过点A′,B′,C′的二次函数的关系式为y=ax2+bx+c,解方程组求出a、b、c的之即可.
22.【答案】解:∵与墙平行的边的长为x(m),则垂直于墙的边长为: /?=(25﹣0.5x)m, 根据题意得出:y=x(25﹣0.5x)=﹣0.5x2+25x
【考点】根据实际问题列二次函数关系式
【解析】【分析】根据已知表示出矩形的长与宽进而表示出面积即可.
23.【答案】解:(1)∵抛物线y=x2+(m+4)x-2(m+6)(m为常数,m≠-8))的对称轴为x=?
??+4
2
,而抛物线与x轴有两个不同的交点A、B,点A、点B关于直线x=1对称, ∴x=?
??+4
2
=1,解得m=-6. ∴所求抛物经的解析式为y=x2-2x. (2)当y=0时,x2-2x=0,解得x1=0,x2=2. 又y=x2-2x=(x-1)2-1, ∴点A、B、C的坐标.分别为(0,0),(2,0),(1,-1).
【考点】二次函数的性质,抛物线与x轴的交点
【解析】【分析】(1)根据已知条件知,该抛物线的对称轴是x=1,然后利用抛物线对称轴方程列出关于m的方程/, 则易求m的值; (2)根据(1)中的函数解析式知,分别求当x=0,y的值;当y=0时,x的值.
24.【答案】解:∵a=-
1
2
<0, ∴y有最大值. 当x=-
3
2×(?
1
2
)
=3时, y最大=
4×(?
1
2
)×2?
3
2
4×(?
1
2
)
=
13
2
, 即小球能达到的最大高度是
13
2
m.
【考点】二次函数的最值
【解析】【分析】根据a的值可得出y有最大值,将函数解析式配方成顶点式(或代入顶点公式),就可求出答案。
25.【答案】解:(1)由题意可得:/, 解①得:m1=3,m2=﹣1, 由②得:m≠0且m≠﹣1, ∴m=3, ∴y=12x2+9; (2)y=﹣x2+5x﹣7 =﹣(x2﹣5x+
25
4
﹣
25
4
)﹣7 =﹣(x﹣
5
2
)2+
25
4
﹣7 =﹣(x﹣
5
2
)2﹣
3
4
. , 顶点坐标为:(
5
2
, ﹣
3
4
),有最大值为:﹣
3
4
.
【考点】二次函数的定义
【解析】【分析】(1)直接利用二次函数的定义得出方程与不等式求出即可; (2)利用配方法求出其顶点坐标即可.
26.【答案】(1)解:w=(x﹣18)y=(x﹣18)(﹣2x+100)
=﹣2x2+136x﹣1800,
∴z与x之间的函数解析式为z=﹣2x2+136x﹣1800(x>18)
(2)解:∵w=﹣2x2+136x﹣1800=﹣2(x﹣34)2+512,
∴当x=34时,w取得最大,最大利润为512万元.
答:当销售单价为34元时,厂商每周能获得最大利润,最大利润是512万元.
(3)解:周销售利润=周销量×(单件售价﹣单件制造成本)=(﹣2x+100)(x﹣18)=﹣2x2+136x﹣1800,
由题意得,﹣2x2+136x﹣1800=350,
解得:x1=25,x2=43,
∵销售单价不得高于30元,
∴x取25,
答:销售单价定为25元时厂商每周能获得350万元的利润;
【考点】二次函数的实际应用-销售问题
【解析】【分析】(1)每只节能灯的利润为:(x﹣18)元,根据总利润等于单只的利润乘以销售数量y,而y=﹣2x+100,再整体替换即可列出W与x之间的函数关系式; (2)根据(1)列函数解析式的性质即可得出答案; (3)将W=350代入(1)列函数解析式,解方程,求出对应的x的值,再根据销售单价不得高于30元检验,即可得出答案。
27.【答案】解:(1)∵A、D关于点Q成中心对称,HQ⊥AB, ∴∠HQD=∠C=90°,HD=HA, ∴∠HDQ=∠A, ∴△DHQ∽△ABC. (2)①如图1,当03
4
x, 此时y=
1
2
(10-4x)×
3
4
x=-
3
2
x2+
15
4
x.. 当x=
5
4
时,最大值y=
75
32
. ②如图2,当2.53
4
x, 此时y=
1
2
(4x-10)×
3
4
x=
3
2
x2-
15
4
x.. 当x=5时,最大值y=
75
4
. ∴y与x之间的函数解析式为y=
?
3
2
??
2
+
15
4
??
03
2
??
2
?
15
4
??
2.5 y的最大值是
75
4
. // (3)①如图1,当0????
cos∠??
=
5
4
x, DE=10-4x, ∴10-4x=
5
4
x,x=
40
21
. 显然ED=EH,HD=HE不可能; ②如图2,当2.55
4
x,x=
40
11
; 若HD=HE,此时点D,E分别与点B,A重合,x=5; 若ED=EH,则△EDH∽△HDA, ∴
????
????
=
????
????
,
4???10
5
4
??
=
5
4
??
2??
,x=
320
103
.? ∴当x的值为
40
21
,
40
11
,5,
320
103
,时,△HDE是等腰三角形
【考点】二次函数的最值,等腰三角形的判定,相似三角形的判定与性质
【解析】【分析】 (1)由两个对应角相等,满足了两个三角形相似的条件。 (2)根据函数解析式可以求得函数最大值。
28.【答案】(1)解:直线解析式 ??=???4 ,令 ??=0 ,得 ??=?4 ;令 ??=0 ,得 ??=4 .∴ ??(4,?0) 、 ??(0,??4) .∵点 ?? 、 ?? 在抛物线 ??=
1
3
??
2
+????+?? 上,∴ {
16
3
+4??+??=0
??=?4
,解得 {
??=?
1
3
??=?4
,∴抛物线解析式为: ??=
1
3
??
2
?
1
3
???4 .令 ??=
1
3
??
2
?
1
3
???4=0 ,解得: ??=?3 或 ??=4 ,∴ ??(?3,?0) . (2)解: ∠??????+∠??????=
45
°
,设 ??(??,???) ,①当 ????⊥???? 时,如答图 2?1 所示./∵ ∠??????=
45
°
,∴ ∠??????+∠??????=
45
°
,故点 ?? 满足条件.过点
??
1
作
??
1
??⊥?? 轴于点 ?? ,则
??
1
??=?? , ????=??? ,∴ ????=4+?? .∵ tan∠
??
1
????=tan∠??????=
4
3
,∴
??
4+??
=
4
3
,∴直线 ??
??
1
的解析式为: ??=
3
4
???4 .联立 ??=
3
4
???4 与 ??=
1
3
??
2
?
1
3
???4 ,得:
3
4
???4=
1
3
??
2
?
1
3
???4 ,解得:
??
1
=0 ,
??
2
=
13
4
,∴
??
1
=?4 ,
??
2
=?
25
16
,∴
??
1
(
13
4
,??
25
16
) ; ②当 ???? 与 ???? 关于 ?? 轴对称时,如答图 2?2 所示./∵ ∠??????=∠??????+∠??????=
45
°
, ∠??????=∠?????? ,∴ ∠??????+∠??????=
45
°
,故点 ?? 满足条件.过点
??
2
作
??
2
??⊥?? 轴于点 ?? ,则
??
2
??=?? , ????=?? ,∴ ????=4+?? .∵ tan∠
??
2
????=tan∠??????=
3
4
,∴
??
4+??
=
3
4
,∴直线 ??
??
2
的解析式为: ??=
4
3
???4 .联立 ??=
4
3
???4 与 ??=
1
3
??
2
?
1
3
???4 得:
4
3
???4=
1
3
??
2
?
1
3
???4 ,解得:
??
1
=0 ,
??
2
=5 ,∴
??
1
=?4 ,
??
2
=
8
3
,∴
??
2
(5,?
8
3
) .综上所述,满足条件的点 ?? 的坐标为: (
13
4
,??
25
16
) 或 (5,?
8
3
) (3)解:设 ∠??????=?? ,则 tan??=
4
3
, sin??=
4
5
, cos??=
3
5
.假设存在满足条件的点 ?? ,设菱形的对角线交于点 ?? ,设运动时间为 ?? . ①若以 ???? 为菱形对角线,如答图 3?1 .此时 ????=?? ,菱形边长 =?? . /∴ ????=
1
2
????=
1
2
(5???) . 在 ????△?????? 中, cos??=
????
????
=
1
2
(5???)
??
=
3
5
, 解得 ??=
25
11
.∴ ????=5???=
30
11
.过点 ?? 作 ????⊥?? 轴于点 ?? , 则 ????=?????sin??=
24
11
, ????=?????cos??=
18
11
, ∴ ????=3?????=
15
11
.∴ ??(?
15
11
,??
24
11
) .∵点
??
1
与点 ?? 横坐标相差 ?? 个单位, ∴
??
1
(?
40
11
,??
24
11
) ; ②若以 ???? 为菱形对角线,如答图 3?2 .此时 ????=?? ,菱形边长 =?? .?? / ∵ ????=????=?? ,∴ ??=
5
2
,点 ?? 为 ???? 中点, ∴ ??(?
3
2
,??2) .∵点
??
2
与点 ?? 横坐标相差 ?? 个单位,∴
??
2
(1,??2) ;③若以 ???? 为菱形对角线,如答图 3?3 .此时 ????=?? ,菱形边长 =5??? . / 在 ????△?????? 中, cos??=
????
????
=
1
2
??
5???
=
3
5
, 解得 ??=
30
11
.∴ ????=3?????=3?
1
2
??=
18
11
,
??
3
??=????=?????sin??=(5?
30
11
)×
4
5
=
20
11
. ∴
??
3
(?
18
11
,?
20
11
) .综上所述,存在满足条件的点 ?? ,点 ?? 坐标为: (?
40
11
,??
24
11
) 或 (1,??2) 或 (?
18
11
,?
20
11
) .
【考点】待定系数法求二次函数解析式,二次函数与一次函数的综合应用,二次函数的实际应用-几何问题
【解析】【分析】(1)根据直线与坐标轴交点的坐标特点求出A,B两点的坐标,将A,B两点的坐标分别代入抛物线 y=
1
3
x2+bx+c得出关于b,c的方程组,求解得出b,c的值,从而得出抛物线的解析式,再根据抛物线与x轴交点的纵坐标是0,将y=0代入抛物线的解析式,楸树对应的自变量的值,从而求出C点的坐标; (2)设 M ( x , ? y )①当BM⊥BC 时,如答图 2 ? 1 所示.根据等腰直角三角形的性质及垂直的定义得出∠MBA+∠CBO=45° ,故点 M 满足条件,过点 M1 作M1E⊥y轴于点E ,则M1E=x , OE=?y 进而表示出BE,根据同角的余角相等及等角的同名三角函数值相等得出 tan∠M1BE=tan∠BCO=
4
3
, 根据正切函数的定义得出关于x,y的方程,变形即可得出直线BM1 的解析式,解联立直线BM 1 的解析式与抛物线的解析式组成的方程组,即可求出M1的坐标;②当 BM与BC关于y轴对称时,如答图 2 ? 2 所示.根据根据角的和差及对称的性质得出∠ABO=∠MBA+∠MBO=45° , ∠MBO=∠CBO ,故∠MBA+∠CBO=45° ,故点 M 满足条件过点 M2 作 M2E⊥y 轴于点 E ,则M2E=x , OE=?y 进而表示出BE,根据同角的余角相等及等角的同名三角函数值相等得出 tan∠M2BE=tan∠CBO=
3
4
, 根据正切函数的定义得出关于x,y的方程,变形即可得出直线BM2 的解析式,解联立直线BM2 的解析式与抛物线的解析式组成的方程组,即可求出M2的坐标,综上所述即可得出M点的坐标; (3)设 ∠BCO=θ ,则 tanθ=?
4
3
, sinθ=?
4
5
, cosθ=
3
5
. 假设存在满足条件的点 D ,设菱形的对角线交于点 E ,设运动时间为 t .①若以 CQ为菱形对角线,如答图 3 ? 1 .此时 BQ=t ,菱形边长=t ,根据菱形的对角线互相平分得出 CE=
1
2
CQ=
1
2
(5?t) ,根据余弦函数的定义,由cosθ=
????
????
,即可列出方程,求解得出t的值,进而得出CQ的值,过点Q作QF⊥x 轴于点 F,则 QF=CQ ? sinθ, CF=CQ ? cosθ,分别计算出QF,CF的长,进而得出OF的长,从而得出Q点的坐标,根据点 D1与点Q横坐标相差 t 个单位即可得出D1的坐标;②若以PQ为菱形对角线,如答图 3 ? 2 .此时 BQ=t ,菱形边长=t,根据线段中点坐标公式,由点 Q为BC中点得出Q点的坐标,根据点 D2与点Q横坐标相差 t 个单位即可得出D1的坐标;③若以CP为菱形对角线,如答图 3 ? 3 .此时BQ=t ,菱形边长=5?t.根据cosθ =
????
????
列出方程,求解得出t的值,进而求出OE, 由 D3E=QE=CQ ? sinθ,从而得出D3的坐标,综上所述即可得出答案。
一、单选题(共10题;共30分)
1.将二次函数??=
??
2
?4???1化为??=
????
2
+??的形式,结果为(????? )
A.???=
??+2
2
+5????????????/B.???=
??+2
2
?5????????????/C.???=
???2
2
+5????????????/D.???=
???2
2
?5
2.把抛物线 ??=
??
2
向右平移1个单位,再向上平移3个单位,得到抛物线的解析式为(?? )
A.???=
(???1)
2
+3??????????????/B.???=
(??+1)
2
?3??????????????/C.???=
(???1)
2
?3??????????????/D.???=
(??+1)
2
+3
3.函数y=(x+1)2-2的最小值是( ??)
A.?1 ????????????????????????????????????/B.?-1 ????????????????????????????????????/C.?2 ????????????????????????????????????/D.?-2
4.如图,抛物线y=ax2+bx+c(a>0)过点(1,0)和点(0,-2),且顶点在第三象限,设P=a-b+c,则P的取值范围是( ??)
/
A.?-1<P<0??????????????????????????/B.?-2<P<0??????????????????????????/C.?-4<P<-2??????????????????????????/D.?-4<P<0
5.
抛物线y=-(x+2)2-3的顶点坐标是?? (? ?? )
A.?(-2,3)??????????????????????/B.?(2,3)??????????????????????/C.?(-2,-3)??????????????????????/D.?(2,-3)
6.把抛物线y=ax2+bx+c的图象向右平移3个单位,再向下平移2个单位,所得图象的解析式为y=x2-2x+3,则b+c的值为(????)
A.?9?????????????????????????????????????????/B.?12?????????????????????????????????????????/C.?-14?????????????????????????????????????????/D.?10
7.在下列函数关系式中,y是x的二次函数的是( )
A.?
??
??
=6?????????????????????????????B.?????=?6?????????????????????????????C.???+
??
2
=6?????????????????????????????D.???=?6??
8.下列关系中,是二次函数关系的是( ? ?)
A.?当距离S一定时,汽车行驶的时间t与速度v之间的关系。 B.?在弹性限度时,弹簧的长度y与所挂物体的质量x之间的关系。 C.?圆的面积S与圆的半径r之间的关系。 D.?正方形的周长C与边长a之间的关系。
9.抛物线y=ax2+bx+c的图角如图,则下列结论:①abc>0;②a+b+c=2;③a>
1
2
?;④b<1. 其中正确的结论是( ) /
A.?①②?????????????????????????????????????B.?②③?????????????????????????????????????C.?②④?????????????????????????????????????D.?③④
10.二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论: ①2a+b=0; ②a+c>b;③抛物线与x轴的另一个交点为(3,0);④abc>0. 其中正确的结论的个数是(?? ) /
A.?1个???????????????????????????????????????B.?2个???????????????????????????????????????C.?3个???????????????????????????????????????D.?4个
二、填空题(共10题;共30分)
11.二次函数y=x2+4x+5中,当x=________时,y有最小值.
12.若将二次函数y=x2-2x+3配方为y=(x-h)2 +k的形式,则y=________.
13.已知抛物线 ??=2
??
2
?????+3 的对称轴是直线 ??=1 ,则 ?? 的值为________.
14.将函数 ??=?
??
2
所在的坐标系先向左平移 2 个单位再向下平移 3 个单位,则函数在新坐标系中的函数关系式是________.
15.把抛物线y=x2 向右平移3个单位,再向下平移1个单位,则得到抛物线________.
16.如图.已知二次函数y1=ax2+bx+c与一次函数y2=kx+m的图象相交于点A(﹣2,4),B(8,2),根据图象能使y1>y2成立的x取值范围是________. /
17.张力同学在校运动会上投掷标枪,标枪运行的高度h(m)与水平距离x(m)的关系式为h=﹣
1
48
x2+
46
48
x+2,则大力同学投掷标枪的成绩是________m.
18.已知点 ?? ? (?3,??) 和点 ?? ? (1,??) 是抛物线 ??=2
??
2
+????+3 图象上的两点,则 ?? =________.
19.二次函数y=ax/+bx+c的图像如图所示,则不等式ax/+bx+c>0的解集是________?. /
20.二次函数 ??=??
??
2
+????+??(??≠0) 的部分图像如图所示,图像过点 (?1,0) ,对称轴为直线 ??=2 ,下列结论:(1) 4??+??=0 ;(2) 9??+??>3?? ;(3)若点 ??(?3,
??
1
) 、点 ??(?
1
2
,
??
2
) 、点 ??(
7
2
,
??
3
) 在该函数图像上,则
??
1
<
??
3
<
??
2
;(4)若方程 ??(??+1)(???5)=?3 的两根为
??
1
和
??
2
,且
??
1
<
??
2
,则
??
1
??
2
.其中正确结论的序号是________. /
三、解答题(共8题;共60分)
21.如图,在平面直角坐标系中,点A,B,C的坐标分别为(0,2),(3,2),(2,3). (1)请在图中画出△ABC向下平移3个单位的像△A′B′C′; (2)若一个二次函数的图象经过(1)中△A′B′C′的三个顶点,求此二次函数的关系式. /
22.如图,用50m长的护栏全部用于建造一块靠墙的长方形花园,写出长方形花园的面积y(m2)与它与墙平行的边的长x(m)之间的函数. /
23.已知抛物线y=x2+(m+4)x-2(m+6)(m是常数,m≠-8)与x轴有两个不同的交点A、B,点A、点B关于直线x=1对称,抛物线的顶点为C. (1)此抛物线的解析式; (2)求点A、B、C的坐标.
24.向上抛掷一个小球,小球在运行过程中,离地面的距离为y(m),运行时间为x(s),y与x之间存在的关系为y=-
1
2
x2+3x+2.问:小球能达到的最大高度是多少?
25.(1)已知y=(m2+m)
??
??
2
?2???1
+(m﹣3)x+m2是x的二次函数,求出它的解析式. (2)用配方法求二次函数y=﹣x2+5x﹣7的顶点坐标并求出函数的最大值或最小值.
26.永嘉某商店试销一种新型节能灯,每盏节能灯进价为18元,试销过程中发现,每周销量y(盏)与销售单价x(元)之间关系可以近似地看作一次函数y=﹣2x+100.(利润=售价﹣进价) (1)写出每周的利润w(元)与销售单价x(元)之间函数解析式;
(2)当销售单价定为多少元时,这种节能灯每周能够获得最大利润?最大利润是多少元? (3)物价部门规定,这种节能灯的销售单价不得高于30元.若商店想要这种节能灯每周获得350元的利润,则销售单价应定为多少元?
27.如图,Rt△ABC中,∠C=90°,BC=6,AC=8.点P,Q都是斜边AB上的动点,点P从B 向A运动(不与点B重合),点Q从A向B运动,BP=AQ.点D,E分别是点A,B以Q,P为对称中心的对称点, HQ⊥AB于Q,交AC于点H.当点E到达顶点A时,P,Q同时停止运动.设BP的长为x,△HDE的面积为y. (1)求证:△DHQ∽△ABC; (2)求y关于x的函数解析式并求y的最大值; (3)当x为何值时,△HDE为等腰三角形? /
28.如图,直线 ??=???4 与 ?? 轴、 ?? 轴分别交于 ?? 、 ?? 两点,抛物线 ??=
1
3
??
2
+????+?? 经过 ?? 、 ?? 两点,与 ?? 轴的另一个交点为 ?? ,连接 ???? .
/
(1)求抛物线的解析式及点 ?? 的坐标;
(2)点 ?? 在抛物线上,连接 ???? ,当 ∠??????+∠??????=
45
°
时,求点 ?? 的坐标;
(3)点 ?? 从点 ?? 出发,沿线段 ???? 由 ?? 向 ?? 运动,同时点 ?? 从点 ?? 出发,沿线段 ???? 由 ?? 向 ?? 运动, ?? 、 ?? 的运动速度都是每秒 1 个单位长度,当 ?? 点到达 ?? 点时, ?? 、 ?? 同时停止运动,试问在坐标平面内是否存在点 ?? ,使 ?? 、 ?? 运动过程中的某一时刻,以 ?? 、 ?? 、 ?? 、 ?? 为顶点的四边形为菱形?若存在,直接写出点 ?? 的坐标;若不存在,说明理由.
答案解析部分
一、单选题
1.【答案】D
【考点】二次函数的三种形式
【解析】【分析】??=
??
2
?4???1=
???2
2
?5. 故选D.
2.【答案】D
【考点】二次函数图象的几何变换
【解析】【解答】 抛物线 ??=
??
2
先向右平移1个单位所得抛物线的解析式为 ??=
(???1)
2
, 抛物线 ??=
(???1)
2
再向上平移3个单位所得抛物线的解析式为 ??=
(???1)
2
+3 , 故答案为:D. 【分析】根据函数图象平移的法则即可得到结果.
3.【答案】D
【考点】二次函数的最值
【解析】【分析】此函数的最小值,在x=-1时,y=-2,此时取最小值。 故选D. 【点评】二次函数的解析式有三种形式:(1)一般式:y=ax2+bx+c(a≠0,a、b、c为常数);(2)顶点式:y=a(x-h)2+k;(3)交点式(与x轴):y=a(x-x1)(x-x2).
4.【答案】D
【考点】二次函数图象与系数的关系,二次函数图象上点的坐标特征
【解析】【解答】解:∵二次函数的图象开口向上,∴a>0
∵对称轴在y轴的左边,∴ ?
??
2??
<0。∴b>0
∵图象与y轴的交点坐标是(0,﹣2),过(1,0)点,代入得:a+b﹣2=0
∴a=2﹣b,b=2﹣a;
∴y=ax2+(2﹣a)x﹣2
把x=﹣1代入得:y=a﹣(2﹣a)﹣2=2a﹣4,
∵b>0,∴b=2﹣a>0
∴a<2
∵a>0,∴0<a<2
∴0<2a<4
∴﹣4<2a﹣4<0,即﹣4<P<0.
故答案为:D.
【分析】将(0,﹣2),(1,0)代入二次函数可得c=-2,a+b﹣2=0,可将b=2﹣a代入(或将a=2-b代入)P=a-b+c=2a-4,则可得P是关于a的一次函数,要求P的取值范围,则需要求a取值范围;观察二次函数的图象可得a>0,且?
??
2??
<0,则b<0,即2-a<0,求出a的取值范围后再求P的范围。
5.【答案】A
【考点】二次函数的三种形式
【解析】【分析】已知解析式为顶点式,可直接根据顶点式的坐标特点,求顶点坐标,从而得出对称轴. 【解答】y=-(x+2)2-3是抛物线的顶点式, 根据顶点式的坐标特点可知,顶点坐标为(-2,-3). 故答案为C. 【点评】此题主要考查了二次函数的性质,关键是熟记:顶点式y=a(x-h)2+k,顶点坐标是(h,k),对称轴是x=h.
6.【答案】B
【考点】二次函数图象与几何变换
【解析】【分析】先化解析式y=x2-2x+3为顶点式,再根据二次函数的平移规律求解即可. y=x2-2x+3=(x-1)2+2 则把抛物线y=(x-1)2+2的图象向左平移3个单位,再向上平移2个单位后的解析式为 y=(x+2)2+4=x2+4x+8 所以b=4,c=8,b+c=12 故选B.
7.【答案】C
【考点】二次函数的定义
【解析】【解答】A、
??
??
=6,可化为y=
1
6
x的形式,不符合二次函数的一般形式,故本选项错误;B、xy=﹣6符合反比例函数的一般形式,不符合二次函数的一般形式,故本选项错误;C、y+x2=6可化为y=-x2+6,符合二次函数的一般形式,故本选项正确;D、y=﹣6x符合正比例函数的一般形式,不符合二次函数的一般形式,故本选项错误.故选C. 【分析】根据二次函数的定义对四个选项进行逐一分析即可,即一般地,形如y=ax2+bx+c(a、b、c是常数,a≠0)的函数,叫做二次函数.
8.【答案】C
【考点】二次函数的定义
【解析】【解答】由题意,A的解析式为 /,B的解析式为 /,C的解析式为 /,D的解析式为 /,唯有B是二次函数关系,故选C. 【分析】能够运用实际问题的意义列出正确的解析式,并进行分析判断是否是二次函数,要根据二次函数的定义的基本要求.
9.【答案】B
【考点】二次函数图象与系数的关系,二次函数图象上点的坐标特征
【解析】
【分析】由图象可知a>0,b>0,c<0;再由特殊点可以判定对错.
【解答】由图象可知a>0,b>0,c<0,∴abc<0;故①错误; 由(1,2)代入抛物线方程可得a+b+c=2;故②正确; 当x=-1时y<0,即a-b+c<0(1), 由②a+b+c=2可得:c=2-a-b(2), 把(2)式代入(1)式中得:b>1;故④错误; ∵对称轴公式-
??
2??
>-1, ∴2a>b, ∵b>1, ∴2a>1,即a>
1
2
;故③正确. 故选B.
10.【答案】B
【考点】二次函数图象与系数的关系
【解析】【解答】解:∵抛物线的对称轴为直线x=﹣
??
2??
?=1, ∴b=﹣2a,即2a+b=0,所以①正确; ∵x=﹣1时,y<0, ∴a﹣b+c<0,即a+c<b,所以②错误; ∵点(﹣2,0)关于直线x=1的对称点为(4,0), ∴抛物线与x轴的另一个交点为(4,0),所以③错误; ∵抛物线开口向上, ∴a>0, ∴b=﹣2a<0, ∵抛物线与y轴的交点在x轴下方, ∴c<0, ∴abc>0,所以④正确. 故选B. 【分析】利用抛物线的对称轴为直线x=﹣
??
2??
?=1,则可对①进行判断;利用x=﹣1时,函数值为负数可对②进行判断;通过求出点(﹣2,0)关于直线x=1的对称点为(4,0)可对③进行判断;由抛物线开口向上得到a>0,则b=﹣2a<0,再由抛物线与y轴的交点在x轴下方得到c<0,则可对④进行判断.
二、填空题
11.【答案】﹣2
【考点】二次函数的最值
【解析】【解答】解:∵二次函数y=x2+4x+5可化为y=(x+2)2+1, ∴当x=﹣2时,二次函数y=x2+4x+5有最小值. 故答案为:﹣2. 【分析】先用配方法把函数化为顶点式的形式,再根据其解析式即可求解.
12.【答案】??=
(???1)
2
+2
【考点】二次函数y=ax^2+bx+c与二次函数y=a(x-h)^2+k的转化
【解析】【解答】y=
??
2
?2??+3 ?=(
??
2
?2??+1 )+2= (???1
)
2
+2.故答案为 ??=
(???1)
2
+2 .
【分析】将二次函数的一般式配方成顶点式。
13.【答案】b=4
【考点】二次函数y=ax^2+bx+c的性质
【解析】【解答】由抛物线的对称轴x=-
??
2??
和已知条件抛物线y=2
??
2
-bx+3的对称轴是直线x=1,得到的等式,即可求出b的值.
【分析】根据抛物线的对称轴直线公式建立方程,求解即可求出b的值。
14.【答案】??=?
(???2)
2
+3
【考点】二次函数图象的几何变换
【解析】【解答】坐标系移动,等同于函数向相反的方向移动,则可得移动后函数为: ??=?
(???2)
2
+3 , 故答案为: ??=?
(???2)
2
+3 . 【分析】根据二次函数图像的平移规律:上加下减,左加右减,将抛物线y=ax2向上或向下平移m个单位,再向左或向右平移n个单位即得到y=a(x±n)2±m。根据平移规则即可得出平移后的抛物线的解析式。
15.【答案】y=(x﹣3)2﹣1
【考点】二次函数图象与几何变换
【解析】【解答】解:抛物线y=x2向右平移3个单位,得:y=(x﹣3)2; 再向下平移1个单位,得:y=(x﹣3)2﹣1. 故答案是:y=(x﹣3)2﹣1. 【分析】根据二次函数图象左加右减,上加下减的平移规律进行解答即可.
16.【答案】x<﹣2或x>8
【考点】二次函数与不等式(组)
【解析】【解答】解:∵A(﹣2,4)、B(8,2), ∴不等式ax2+bx+c>kx+m成立的x的取值范围是x<﹣2或x>8. 故答案为x<﹣2或x>8. 【分析】根据函数图象写出抛物线在直线上方部分的x的取值范围即可
17.【答案】48
【考点】因式分解法解一元二次方程,二次函数图像与坐标轴的交点问题
【解析】【解答】解:∵h=﹣
1
48
x2+
46
48
x+2, ∴当h=0时,0=﹣
1
48
x2+
46
48
x+2, 解得,x1=﹣2,x2=48, 即大力同学投掷标枪的成绩是48m, 故答案为:48. 【分析】先根据h=0时,建立关于x的方程求解,即可得出答案。
18.【答案】b=4
【考点】二次函数图象与系数的关系
【解析】【解答】把A(-3,m)和点B(1,m)代入y=2x2+bx+3得: {
??=2×9?3??+3
??=2+??+3
,解得:b=6
【分析】把点A和点B的坐标代入抛物线的解析式,求出b的值.
19.【答案】﹣3<x<1
【考点】二次函数的图象,抛物线与x轴的交点,二次函数与不等式(组)
【解析】【解答】由图可知,一元二次不等式ax2+bx+c>0的解是﹣3<x<1. 故答案是﹣3<x<1. 【分析】考查二次函数与不等式(组).
20.【答案】(1)(4)
【考点】二次函数图象与系数的关系
【解析】【解答】:∵抛物线的对称轴为直线x=-
??
2??
=2,∴b=-4a>0,即4a+b=0,所以(1)正确;∵x=-3时,y<0,∴9a-3b+c<0,即9a+c<3b,所以(2)错误;∵抛物线的对称轴为直线x=-
??
2??
=2,图象与x轴交于(-1,0), ∴抛物线x轴的另一个交点是(5,0),∵点A(-3,y1)、点B(-
1
2
,y2)、点C(
7
2
,y3),∵
7
2
-2=
3
2
,2-(-
1
2
)=
5
2
,∴
3
2
<
5
2
∴点C离对称轴的距离近,∴y3>y2 , ∵a<0,-3<-
1
2
<2,∴y1<y2∴y1<y2<y3 , 故(3)错误.如图, / ∵a<0,∴(x+1)(x-5)=-3/a>0,即(x+1)(x-5)>0,故x<-1或x>5,故(4)正确. 【分析】由抛物线的对称轴直线,得到4a+b=0,图象与x轴交于(-1,0),得到抛物线x轴的另一个交点,由已知得到点C离对称轴的距离近,得到y3>y2 , 由a<0,得到y1<y2<y3.
三、解答题
21.【答案】(1)如图: / (2)由题意得A′,B′,C′的坐标分别是(0,﹣1),(3,﹣1),(2,0), 设过点A′、B′、C′的二次函数的关系式为y=ax2+bx+c, 则有
??=?1
9??+3??+??=?1
4??+2??+??=0
, 解得??=?
1
2
,??=
3
2
,??=?1, ∴二次函数的关系式为??=?
1
2
??
2
+
3
2
???1.
【考点】待定系数法求二次函数解析式
【解析】【分析】(1)直接作出图形即可,(2)根据题意写出A′,B′,C′的坐标,设过点A′,B′,C′的二次函数的关系式为y=ax2+bx+c,解方程组求出a、b、c的之即可.
22.【答案】解:∵与墙平行的边的长为x(m),则垂直于墙的边长为: /?=(25﹣0.5x)m, 根据题意得出:y=x(25﹣0.5x)=﹣0.5x2+25x
【考点】根据实际问题列二次函数关系式
【解析】【分析】根据已知表示出矩形的长与宽进而表示出面积即可.
23.【答案】解:(1)∵抛物线y=x2+(m+4)x-2(m+6)(m为常数,m≠-8))的对称轴为x=?
??+4
2
,而抛物线与x轴有两个不同的交点A、B,点A、点B关于直线x=1对称, ∴x=?
??+4
2
=1,解得m=-6. ∴所求抛物经的解析式为y=x2-2x. (2)当y=0时,x2-2x=0,解得x1=0,x2=2. 又y=x2-2x=(x-1)2-1, ∴点A、B、C的坐标.分别为(0,0),(2,0),(1,-1).
【考点】二次函数的性质,抛物线与x轴的交点
【解析】【分析】(1)根据已知条件知,该抛物线的对称轴是x=1,然后利用抛物线对称轴方程列出关于m的方程/, 则易求m的值; (2)根据(1)中的函数解析式知,分别求当x=0,y的值;当y=0时,x的值.
24.【答案】解:∵a=-
1
2
<0, ∴y有最大值. 当x=-
3
2×(?
1
2
)
=3时, y最大=
4×(?
1
2
)×2?
3
2
4×(?
1
2
)
=
13
2
, 即小球能达到的最大高度是
13
2
m.
【考点】二次函数的最值
【解析】【分析】根据a的值可得出y有最大值,将函数解析式配方成顶点式(或代入顶点公式),就可求出答案。
25.【答案】解:(1)由题意可得:/, 解①得:m1=3,m2=﹣1, 由②得:m≠0且m≠﹣1, ∴m=3, ∴y=12x2+9; (2)y=﹣x2+5x﹣7 =﹣(x2﹣5x+
25
4
﹣
25
4
)﹣7 =﹣(x﹣
5
2
)2+
25
4
﹣7 =﹣(x﹣
5
2
)2﹣
3
4
. , 顶点坐标为:(
5
2
, ﹣
3
4
),有最大值为:﹣
3
4
.
【考点】二次函数的定义
【解析】【分析】(1)直接利用二次函数的定义得出方程与不等式求出即可; (2)利用配方法求出其顶点坐标即可.
26.【答案】(1)解:w=(x﹣18)y=(x﹣18)(﹣2x+100)
=﹣2x2+136x﹣1800,
∴z与x之间的函数解析式为z=﹣2x2+136x﹣1800(x>18)
(2)解:∵w=﹣2x2+136x﹣1800=﹣2(x﹣34)2+512,
∴当x=34时,w取得最大,最大利润为512万元.
答:当销售单价为34元时,厂商每周能获得最大利润,最大利润是512万元.
(3)解:周销售利润=周销量×(单件售价﹣单件制造成本)=(﹣2x+100)(x﹣18)=﹣2x2+136x﹣1800,
由题意得,﹣2x2+136x﹣1800=350,
解得:x1=25,x2=43,
∵销售单价不得高于30元,
∴x取25,
答:销售单价定为25元时厂商每周能获得350万元的利润;
【考点】二次函数的实际应用-销售问题
【解析】【分析】(1)每只节能灯的利润为:(x﹣18)元,根据总利润等于单只的利润乘以销售数量y,而y=﹣2x+100,再整体替换即可列出W与x之间的函数关系式; (2)根据(1)列函数解析式的性质即可得出答案; (3)将W=350代入(1)列函数解析式,解方程,求出对应的x的值,再根据销售单价不得高于30元检验,即可得出答案。
27.【答案】解:(1)∵A、D关于点Q成中心对称,HQ⊥AB, ∴∠HQD=∠C=90°,HD=HA, ∴∠HDQ=∠A, ∴△DHQ∽△ABC. (2)①如图1,当0
4
x, 此时y=
1
2
(10-4x)×
3
4
x=-
3
2
x2+
15
4
x.. 当x=
5
4
时,最大值y=
75
32
. ②如图2,当2.53
4
x, 此时y=
1
2
(4x-10)×
3
4
x=
3
2
x2-
15
4
x.. 当x=5时,最大值y=
75
4
. ∴y与x之间的函数解析式为y=
?
3
2
??
2
+
15
4
??
03
2
??
2
?
15
4
??
2.5 y的最大值是
75
4
. // (3)①如图1,当0
cos∠??
=
5
4
x, DE=10-4x, ∴10-4x=
5
4
x,x=
40
21
. 显然ED=EH,HD=HE不可能; ②如图2,当2.55
4
x,x=
40
11
; 若HD=HE,此时点D,E分别与点B,A重合,x=5; 若ED=EH,则△EDH∽△HDA, ∴
????
????
=
????
????
,
4???10
5
4
??
=
5
4
??
2??
,x=
320
103
.? ∴当x的值为
40
21
,
40
11
,5,
320
103
,时,△HDE是等腰三角形
【考点】二次函数的最值,等腰三角形的判定,相似三角形的判定与性质
【解析】【分析】 (1)由两个对应角相等,满足了两个三角形相似的条件。 (2)根据函数解析式可以求得函数最大值。
28.【答案】(1)解:直线解析式 ??=???4 ,令 ??=0 ,得 ??=?4 ;令 ??=0 ,得 ??=4 .∴ ??(4,?0) 、 ??(0,??4) .∵点 ?? 、 ?? 在抛物线 ??=
1
3
??
2
+????+?? 上,∴ {
16
3
+4??+??=0
??=?4
,解得 {
??=?
1
3
??=?4
,∴抛物线解析式为: ??=
1
3
??
2
?
1
3
???4 .令 ??=
1
3
??
2
?
1
3
???4=0 ,解得: ??=?3 或 ??=4 ,∴ ??(?3,?0) . (2)解: ∠??????+∠??????=
45
°
,设 ??(??,???) ,①当 ????⊥???? 时,如答图 2?1 所示./∵ ∠??????=
45
°
,∴ ∠??????+∠??????=
45
°
,故点 ?? 满足条件.过点
??
1
作
??
1
??⊥?? 轴于点 ?? ,则
??
1
??=?? , ????=??? ,∴ ????=4+?? .∵ tan∠
??
1
????=tan∠??????=
4
3
,∴
??
4+??
=
4
3
,∴直线 ??
??
1
的解析式为: ??=
3
4
???4 .联立 ??=
3
4
???4 与 ??=
1
3
??
2
?
1
3
???4 ,得:
3
4
???4=
1
3
??
2
?
1
3
???4 ,解得:
??
1
=0 ,
??
2
=
13
4
,∴
??
1
=?4 ,
??
2
=?
25
16
,∴
??
1
(
13
4
,??
25
16
) ; ②当 ???? 与 ???? 关于 ?? 轴对称时,如答图 2?2 所示./∵ ∠??????=∠??????+∠??????=
45
°
, ∠??????=∠?????? ,∴ ∠??????+∠??????=
45
°
,故点 ?? 满足条件.过点
??
2
作
??
2
??⊥?? 轴于点 ?? ,则
??
2
??=?? , ????=?? ,∴ ????=4+?? .∵ tan∠
??
2
????=tan∠??????=
3
4
,∴
??
4+??
=
3
4
,∴直线 ??
??
2
的解析式为: ??=
4
3
???4 .联立 ??=
4
3
???4 与 ??=
1
3
??
2
?
1
3
???4 得:
4
3
???4=
1
3
??
2
?
1
3
???4 ,解得:
??
1
=0 ,
??
2
=5 ,∴
??
1
=?4 ,
??
2
=
8
3
,∴
??
2
(5,?
8
3
) .综上所述,满足条件的点 ?? 的坐标为: (
13
4
,??
25
16
) 或 (5,?
8
3
) (3)解:设 ∠??????=?? ,则 tan??=
4
3
, sin??=
4
5
, cos??=
3
5
.假设存在满足条件的点 ?? ,设菱形的对角线交于点 ?? ,设运动时间为 ?? . ①若以 ???? 为菱形对角线,如答图 3?1 .此时 ????=?? ,菱形边长 =?? . /∴ ????=
1
2
????=
1
2
(5???) . 在 ????△?????? 中, cos??=
????
????
=
1
2
(5???)
??
=
3
5
, 解得 ??=
25
11
.∴ ????=5???=
30
11
.过点 ?? 作 ????⊥?? 轴于点 ?? , 则 ????=?????sin??=
24
11
, ????=?????cos??=
18
11
, ∴ ????=3?????=
15
11
.∴ ??(?
15
11
,??
24
11
) .∵点
??
1
与点 ?? 横坐标相差 ?? 个单位, ∴
??
1
(?
40
11
,??
24
11
) ; ②若以 ???? 为菱形对角线,如答图 3?2 .此时 ????=?? ,菱形边长 =?? .?? / ∵ ????=????=?? ,∴ ??=
5
2
,点 ?? 为 ???? 中点, ∴ ??(?
3
2
,??2) .∵点
??
2
与点 ?? 横坐标相差 ?? 个单位,∴
??
2
(1,??2) ;③若以 ???? 为菱形对角线,如答图 3?3 .此时 ????=?? ,菱形边长 =5??? . / 在 ????△?????? 中, cos??=
????
????
=
1
2
??
5???
=
3
5
, 解得 ??=
30
11
.∴ ????=3?????=3?
1
2
??=
18
11
,
??
3
??=????=?????sin??=(5?
30
11
)×
4
5
=
20
11
. ∴
??
3
(?
18
11
,?
20
11
) .综上所述,存在满足条件的点 ?? ,点 ?? 坐标为: (?
40
11
,??
24
11
) 或 (1,??2) 或 (?
18
11
,?
20
11
) .
【考点】待定系数法求二次函数解析式,二次函数与一次函数的综合应用,二次函数的实际应用-几何问题
【解析】【分析】(1)根据直线与坐标轴交点的坐标特点求出A,B两点的坐标,将A,B两点的坐标分别代入抛物线 y=
1
3
x2+bx+c得出关于b,c的方程组,求解得出b,c的值,从而得出抛物线的解析式,再根据抛物线与x轴交点的纵坐标是0,将y=0代入抛物线的解析式,楸树对应的自变量的值,从而求出C点的坐标; (2)设 M ( x , ? y )①当BM⊥BC 时,如答图 2 ? 1 所示.根据等腰直角三角形的性质及垂直的定义得出∠MBA+∠CBO=45° ,故点 M 满足条件,过点 M1 作M1E⊥y轴于点E ,则M1E=x , OE=?y 进而表示出BE,根据同角的余角相等及等角的同名三角函数值相等得出 tan∠M1BE=tan∠BCO=
4
3
, 根据正切函数的定义得出关于x,y的方程,变形即可得出直线BM1 的解析式,解联立直线BM 1 的解析式与抛物线的解析式组成的方程组,即可求出M1的坐标;②当 BM与BC关于y轴对称时,如答图 2 ? 2 所示.根据根据角的和差及对称的性质得出∠ABO=∠MBA+∠MBO=45° , ∠MBO=∠CBO ,故∠MBA+∠CBO=45° ,故点 M 满足条件过点 M2 作 M2E⊥y 轴于点 E ,则M2E=x , OE=?y 进而表示出BE,根据同角的余角相等及等角的同名三角函数值相等得出 tan∠M2BE=tan∠CBO=
3
4
, 根据正切函数的定义得出关于x,y的方程,变形即可得出直线BM2 的解析式,解联立直线BM2 的解析式与抛物线的解析式组成的方程组,即可求出M2的坐标,综上所述即可得出M点的坐标; (3)设 ∠BCO=θ ,则 tanθ=?
4
3
, sinθ=?
4
5
, cosθ=
3
5
. 假设存在满足条件的点 D ,设菱形的对角线交于点 E ,设运动时间为 t .①若以 CQ为菱形对角线,如答图 3 ? 1 .此时 BQ=t ,菱形边长=t ,根据菱形的对角线互相平分得出 CE=
1
2
CQ=
1
2
(5?t) ,根据余弦函数的定义,由cosθ=
????
????
,即可列出方程,求解得出t的值,进而得出CQ的值,过点Q作QF⊥x 轴于点 F,则 QF=CQ ? sinθ, CF=CQ ? cosθ,分别计算出QF,CF的长,进而得出OF的长,从而得出Q点的坐标,根据点 D1与点Q横坐标相差 t 个单位即可得出D1的坐标;②若以PQ为菱形对角线,如答图 3 ? 2 .此时 BQ=t ,菱形边长=t,根据线段中点坐标公式,由点 Q为BC中点得出Q点的坐标,根据点 D2与点Q横坐标相差 t 个单位即可得出D1的坐标;③若以CP为菱形对角线,如答图 3 ? 3 .此时BQ=t ,菱形边长=5?t.根据cosθ =
????
????
列出方程,求解得出t的值,进而求出OE, 由 D3E=QE=CQ ? sinθ,从而得出D3的坐标,综上所述即可得出答案。
