第二单元第3课时《探索与发现:三角形内角和》练习题
文档属性
| 名称 | 第二单元第3课时《探索与发现:三角形内角和》练习题 |

|
|
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-03-15 17:32:25 | ||
图片预览

文档简介
《探索与发现:三角形内角和》练习题
填空。
三角形的内角和是( )°。
2.在一个三角形中,有两个角分别是36°和75°,则该三角形的第三个角是( ) 度,这个三角形是( )三角形。
3.在一个三角形中,有两个角都是45°,这个三角形既是( )三角形,又是( )三角形。
4.求出下面角的度数。
∠A=( ) ∠C=( ) ∠B=( )
5.直角三角形的两个锐角和是( )度。
6.把一个长方形分割成两个三角形,每一个小三角形的内角和是( )度。
判断。
把两个相同的小三角形拼成一个大的三角形,这个大三角形的内角和比其它两个小三角形的内角和大。 ( )
2.一个三角形中最多只能有一个直角。 ( )
3.三角形中有一个角是70 o,那么这个三角形一定是个锐角三角形。 ( )
3.一个三角形的三个内角分别是56°、72°、62°。 ( )
三、选一选。
1.把一个三角形分成两个三角形,其中一个三角形的内角和是( )度。
A.比90°小 B.比90°大
C.可能等于90°,大于90°或小于90° D.还是180°
2.在一个三角形中,有两个锐角的和是90°,那么这个三角形是( )。
A.直角三角形 B.锐角三角形
C.钝角三角形 D.无法确定
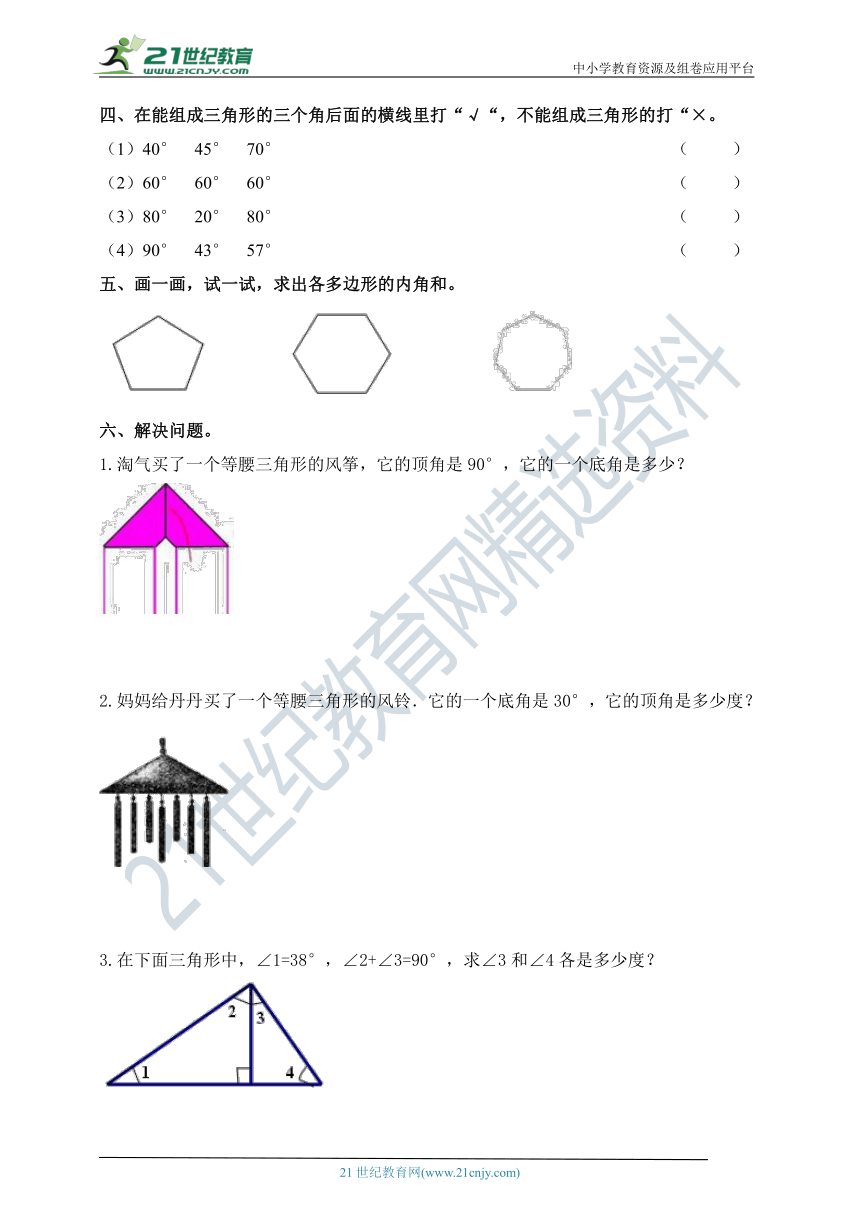
四、在能组成三角形的三个角后面的横线里打“√“,不能组成三角形的打“×。
(1)40° 45° 70° ( )
(2)60° 60° 60° ( )
(3)80° 20° 80° ( )
(4)90° 43° 57° ( )
五、画一画,试一试,求出各多边形的内角和。
六、解决问题。
1.淘气买了一个等腰三角形的风筝,它的顶角是90°,它的一个底角是多少?
2.妈妈给丹丹买了一个等腰三角形的风铃.它的一个底角是30°,它的顶角是多少度?
3.在下面三角形中,∠1=38°,∠2+∠3=90°,求∠3和∠4各是多少度?
答案与解析
一、1.【解析】直接根据三角形的内角和是180°求解。
【答案】180。
2.【解析】根据三角形的内角和定理,求出第三个角,再判断三角形的形状,即第三个角是180°-36°-75°=69°,则这个三角形是锐角三角形。
【答案】69°;锐角。
3.【解析】根据三角形内角和是180°算出剩下的这个角是90°,有一个角是直角的等腰三角形是等腰直角三角形,进而得出结论。
【答案】直角;等腰。
4.【解析】根据三角形内角和是180°,连续减去已知两个角的度数即可求解。
【答案】55°;113°;55°。
5.【解析】根据三角形内角和是180°减去直角的度数即可求出两个锐角和。
【答案】90。
6.【解析】不论三角形的形状大小,内角和都是180度。
【答案】180。
二、1.【解析】只要是三角形,它的内角和就是180度,不管三角形是大还是小,它的内角和都是180度,据此解答。
【答案】×。
2.【解析】依据三角形的内角和是180度,假设一个三角形中可以有多于1个的直角,则会得出违背三角形内角和是180度的结论,假设不成立,从而可以作出正确的判断。
【答案】√。
3.【解析】根据三角形的内角和是180度可知:三角形中有一个角是70度,另两个角的度数和是180-70=110度,另两个角中可能有1个是直角和1个锐角,也可能有1个钝角和1个锐角,还有可能两个角都是锐角,即这个三角形可能是锐角三角形或直角三角形或钝角三角形。
【答案】×。
4.【解析】根据三角形的内角和是180度直接求解。
【答案】×。
三、1.【解析】不论三角形的形状大小,内角和都是180度。
【答案】D。
2.【解析】据三角形内角和是180°,如果两个锐角的和等于90°那么剩下的一个内角一定等于90°即是一个直角,根据锐角三角形的概念:有一个角是直角的三角形是直角三角形,可得这个三角形一定是直角三角形。
【答案】A。
四、【解析】计算一下三个角的度数之和,如果等于180度就能组成三角形,否则不能。
【答案】(1)×,(2)√,(3)√,(4)×。
五、【解析】先从多边形的一个顶点开始把它分成三角形,然后数数一共是几个三角形,是几个,就用几乘180就是该多边形的内角和,据此解答即可。
【答案】
180°×3=540°
180°×4=720°
180°×5=900°
填空。
三角形的内角和是( )°。
2.在一个三角形中,有两个角分别是36°和75°,则该三角形的第三个角是( ) 度,这个三角形是( )三角形。
3.在一个三角形中,有两个角都是45°,这个三角形既是( )三角形,又是( )三角形。
4.求出下面角的度数。
∠A=( ) ∠C=( ) ∠B=( )
5.直角三角形的两个锐角和是( )度。
6.把一个长方形分割成两个三角形,每一个小三角形的内角和是( )度。
判断。
把两个相同的小三角形拼成一个大的三角形,这个大三角形的内角和比其它两个小三角形的内角和大。 ( )
2.一个三角形中最多只能有一个直角。 ( )
3.三角形中有一个角是70 o,那么这个三角形一定是个锐角三角形。 ( )
3.一个三角形的三个内角分别是56°、72°、62°。 ( )
三、选一选。
1.把一个三角形分成两个三角形,其中一个三角形的内角和是( )度。
A.比90°小 B.比90°大
C.可能等于90°,大于90°或小于90° D.还是180°
2.在一个三角形中,有两个锐角的和是90°,那么这个三角形是( )。
A.直角三角形 B.锐角三角形
C.钝角三角形 D.无法确定
四、在能组成三角形的三个角后面的横线里打“√“,不能组成三角形的打“×。
(1)40° 45° 70° ( )
(2)60° 60° 60° ( )
(3)80° 20° 80° ( )
(4)90° 43° 57° ( )
五、画一画,试一试,求出各多边形的内角和。
六、解决问题。
1.淘气买了一个等腰三角形的风筝,它的顶角是90°,它的一个底角是多少?
2.妈妈给丹丹买了一个等腰三角形的风铃.它的一个底角是30°,它的顶角是多少度?
3.在下面三角形中,∠1=38°,∠2+∠3=90°,求∠3和∠4各是多少度?
答案与解析
一、1.【解析】直接根据三角形的内角和是180°求解。
【答案】180。
2.【解析】根据三角形的内角和定理,求出第三个角,再判断三角形的形状,即第三个角是180°-36°-75°=69°,则这个三角形是锐角三角形。
【答案】69°;锐角。
3.【解析】根据三角形内角和是180°算出剩下的这个角是90°,有一个角是直角的等腰三角形是等腰直角三角形,进而得出结论。
【答案】直角;等腰。
4.【解析】根据三角形内角和是180°,连续减去已知两个角的度数即可求解。
【答案】55°;113°;55°。
5.【解析】根据三角形内角和是180°减去直角的度数即可求出两个锐角和。
【答案】90。
6.【解析】不论三角形的形状大小,内角和都是180度。
【答案】180。
二、1.【解析】只要是三角形,它的内角和就是180度,不管三角形是大还是小,它的内角和都是180度,据此解答。
【答案】×。
2.【解析】依据三角形的内角和是180度,假设一个三角形中可以有多于1个的直角,则会得出违背三角形内角和是180度的结论,假设不成立,从而可以作出正确的判断。
【答案】√。
3.【解析】根据三角形的内角和是180度可知:三角形中有一个角是70度,另两个角的度数和是180-70=110度,另两个角中可能有1个是直角和1个锐角,也可能有1个钝角和1个锐角,还有可能两个角都是锐角,即这个三角形可能是锐角三角形或直角三角形或钝角三角形。
【答案】×。
4.【解析】根据三角形的内角和是180度直接求解。
【答案】×。
三、1.【解析】不论三角形的形状大小,内角和都是180度。
【答案】D。
2.【解析】据三角形内角和是180°,如果两个锐角的和等于90°那么剩下的一个内角一定等于90°即是一个直角,根据锐角三角形的概念:有一个角是直角的三角形是直角三角形,可得这个三角形一定是直角三角形。
【答案】A。
四、【解析】计算一下三个角的度数之和,如果等于180度就能组成三角形,否则不能。
【答案】(1)×,(2)√,(3)√,(4)×。
五、【解析】先从多边形的一个顶点开始把它分成三角形,然后数数一共是几个三角形,是几个,就用几乘180就是该多边形的内角和,据此解答即可。
【答案】
180°×3=540°
180°×4=720°
180°×5=900°
