2.1.4 函数的奇偶性
图片预览











文档简介
美的线条和其他一切美的形体都必须有对称的形式
---毕达哥拉斯
探究一:形象认识
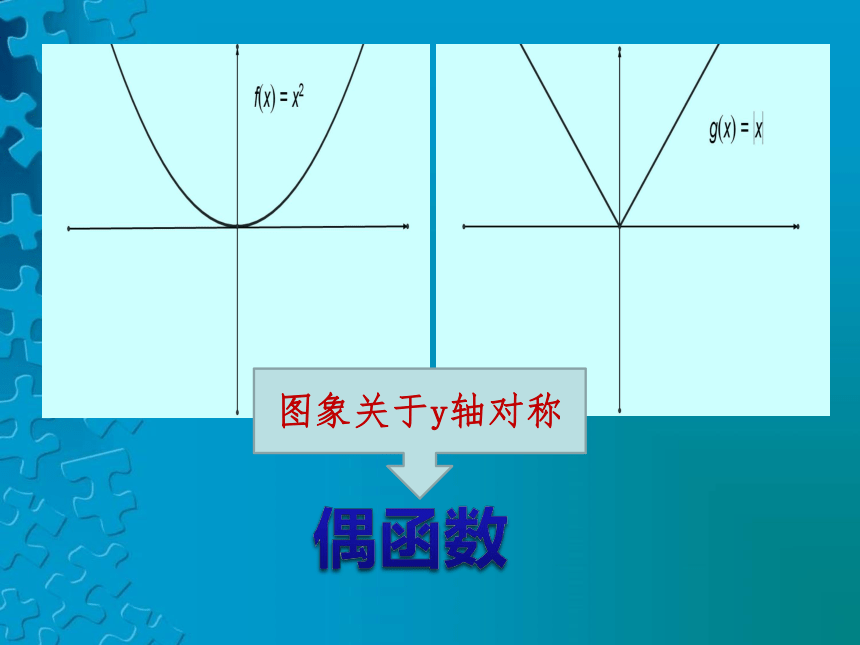
问题:请说出几个图象具有对称美的函数?
图象关于y轴对称
是偶函数吗
提出问题
探究二:什么样的函数图象关于y轴对称
.
.
.
.
x
-x
9
4
1
0
1
4
9
猜:
证:
问题:观察函数f(x)=x2图象,填表,你有什么发现
… -3 -2 -1 0 1 2 3 …
… …
探究二:什么样的函数图象关于y轴对称
.
.
?
.
.
成果展示: 偶函数定义
若f(-x)= f(x),则这个函数叫做偶函数.
设函数y=f(x)的定义域为D,
如果对D内的任意一个x,都有-x∈ D
判断函数f(x)=x2-1和f(x)=x2-1 x∈[-1,3]是否为偶函数
在 [-1,1]上是偶函数?
小试牛刀
1、若f(-2)=f(2),f(-1)=f(1)则函数y=f(x)
一定是偶函数 ( )
2、若f(-2) ≠ f(2),则函数y=f(x)一定不是
偶函数( )
3、存在偶函数的定义域是(-2,2] ( )
探究三:偶函数定义内涵深化
判断正误并简要陈述理由
是的
是偶函数吗
例
解决问题
1、判断下列函数是否为偶函数
①f(x)=x6+x4 ②f(x)=
③f(x)=1
画龙点睛:
f(x)=a(a为常数)且定义域关于
原点对称时f(x)是偶函数
f(x)=1
1
跟踪训练
2、已知偶函数f(x) 在x轴右边的一部分,
求出f(-2)并试作出它在x轴左边的图象
、
跟踪训练
图象关于原点对称
探究四:类比偶函数,探究奇函数定义
问题:观察函数f(x)= 的图象,填函数值对应表,你有什么发现?
探究四:类比偶函数,探究奇函数定义
-1
1
X … -3 -2 -1 1 2 3 …
… …
若f(-x) = - f(x),则这个函数叫做奇函数.
设函数y=f(x)的定义域为D,
如果对D内的任意一个x,都有-x∈ D
定义强调:1、对称性
2、整体性
成果展示: 奇函数定义
成果展示: 奇函数定义
、
学以致用
2、已知定义在R上的奇函数f(x) 在x轴右边的一部分,(1) 求出f(-2),f(0)的值
(2)试作出它在x轴左边的图象
、
学以致用
画龙点睛:
奇函数f(x)在0处有定义,
则必有f(0)=0
1、如果f(x)是奇函数,则f(0)=0( )
2、如果f(0)=0,则f(x)是奇函数( )
3、如果f(x)是偶函数,则f(0)≠0 ( )
判断正误并简要陈述理由
辨析深化
探究:判断函数奇偶性的方法
求定义域,看定义域是否关于原点对称
一定
代入-x,求f(-x)
二代
找f(-x)与f(x)的关系
三找
相等
偶函数
否
非奇非偶
是
都不满足
相反数
奇函数
探究:判断函数奇偶性的方法
1、判断下列函数的奇偶性
(2)
思考与讨论:
辨析深化
画龙点睛:
f(x)=0且定义域关于原点对称时
f(x)既是奇函数又是偶函数
辨析深化
小结:函数按奇偶性可分为
请谈一谈你的收获
数学知识
数学方法
数学思想
---毕达哥拉斯
探究一:形象认识
问题:请说出几个图象具有对称美的函数?
图象关于y轴对称
是偶函数吗
提出问题
探究二:什么样的函数图象关于y轴对称
.
.
.
.
x
-x
9
4
1
0
1
4
9
猜:
证:
问题:观察函数f(x)=x2图象,填表,你有什么发现
… -3 -2 -1 0 1 2 3 …
… …
探究二:什么样的函数图象关于y轴对称
.
.
?
.
.
成果展示: 偶函数定义
若f(-x)= f(x),则这个函数叫做偶函数.
设函数y=f(x)的定义域为D,
如果对D内的任意一个x,都有-x∈ D
判断函数f(x)=x2-1和f(x)=x2-1 x∈[-1,3]是否为偶函数
在 [-1,1]上是偶函数?
小试牛刀
1、若f(-2)=f(2),f(-1)=f(1)则函数y=f(x)
一定是偶函数 ( )
2、若f(-2) ≠ f(2),则函数y=f(x)一定不是
偶函数( )
3、存在偶函数的定义域是(-2,2] ( )
探究三:偶函数定义内涵深化
判断正误并简要陈述理由
是的
是偶函数吗
例
解决问题
1、判断下列函数是否为偶函数
①f(x)=x6+x4 ②f(x)=
③f(x)=1
画龙点睛:
f(x)=a(a为常数)且定义域关于
原点对称时f(x)是偶函数
f(x)=1
1
跟踪训练
2、已知偶函数f(x) 在x轴右边的一部分,
求出f(-2)并试作出它在x轴左边的图象
、
跟踪训练
图象关于原点对称
探究四:类比偶函数,探究奇函数定义
问题:观察函数f(x)= 的图象,填函数值对应表,你有什么发现?
探究四:类比偶函数,探究奇函数定义
-1
1
X … -3 -2 -1 1 2 3 …
… …
若f(-x) = - f(x),则这个函数叫做奇函数.
设函数y=f(x)的定义域为D,
如果对D内的任意一个x,都有-x∈ D
定义强调:1、对称性
2、整体性
成果展示: 奇函数定义
成果展示: 奇函数定义
、
学以致用
2、已知定义在R上的奇函数f(x) 在x轴右边的一部分,(1) 求出f(-2),f(0)的值
(2)试作出它在x轴左边的图象
、
学以致用
画龙点睛:
奇函数f(x)在0处有定义,
则必有f(0)=0
1、如果f(x)是奇函数,则f(0)=0( )
2、如果f(0)=0,则f(x)是奇函数( )
3、如果f(x)是偶函数,则f(0)≠0 ( )
判断正误并简要陈述理由
辨析深化
探究:判断函数奇偶性的方法
求定义域,看定义域是否关于原点对称
一定
代入-x,求f(-x)
二代
找f(-x)与f(x)的关系
三找
相等
偶函数
否
非奇非偶
是
都不满足
相反数
奇函数
探究:判断函数奇偶性的方法
1、判断下列函数的奇偶性
(2)
思考与讨论:
辨析深化
画龙点睛:
f(x)=0且定义域关于原点对称时
f(x)既是奇函数又是偶函数
辨析深化
小结:函数按奇偶性可分为
请谈一谈你的收获
数学知识
数学方法
数学思想
