2.2.2 二次函数的性质与图像ppt(21张)
文档属性
| 名称 | 2.2.2 二次函数的性质与图像ppt(21张) |

|
|
| 格式 | zip | ||
| 文件大小 | 464.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-01-17 20:00:31 | ||
图片预览



文档简介
二次函数在闭区间上的最值
高中数学
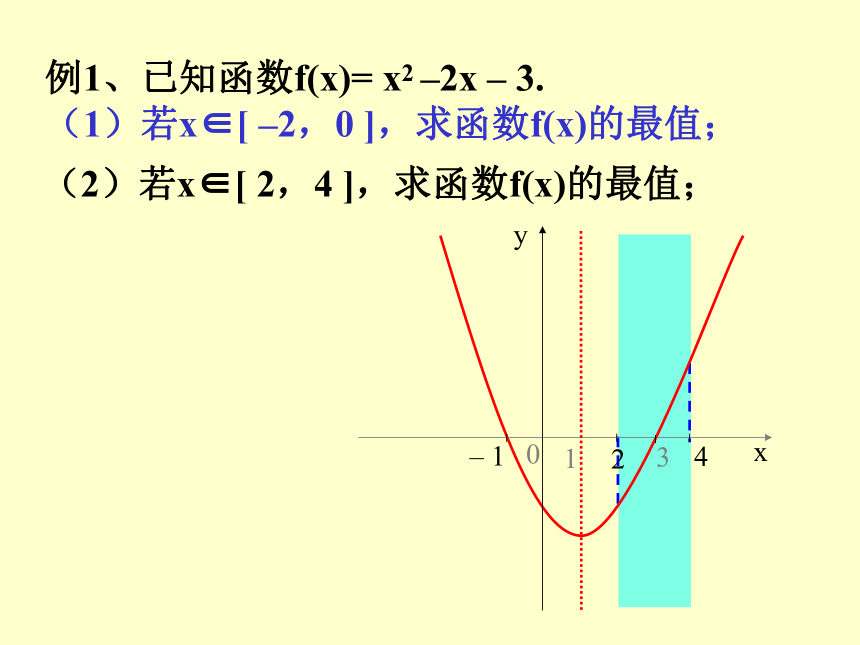
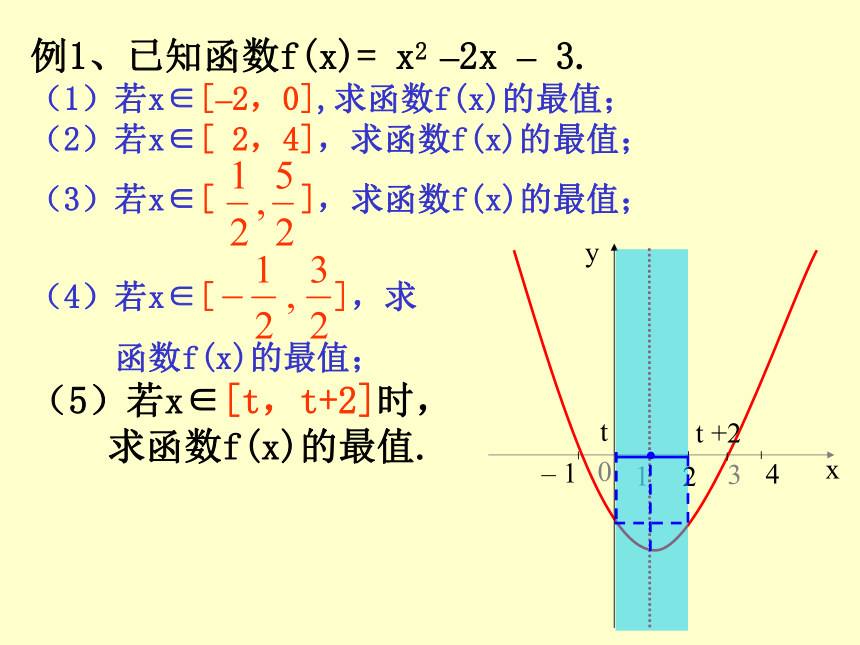
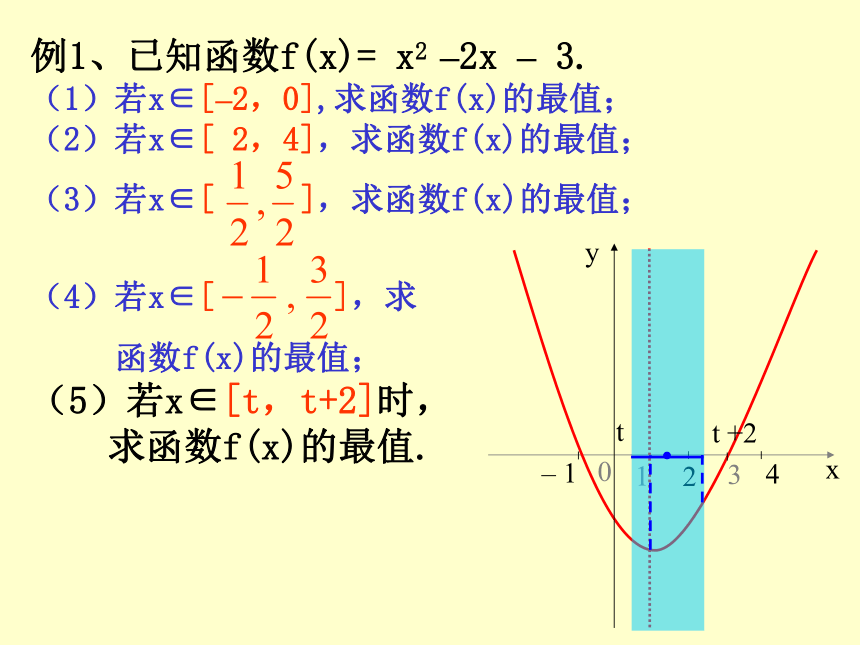
例1、已知函数f(x)= x2–2x –3.
(1)若x∈[ –2,0 ], 求函数f(x)的最值;
轴定区间定时的值域与最值
例1、已知函数f(x)= x2 –2x – 3.
(1)若x∈[ –2,0 ],求函数f(x)的最值;
(2)若x∈[ 2,4 ],求函数f(x)的最值;
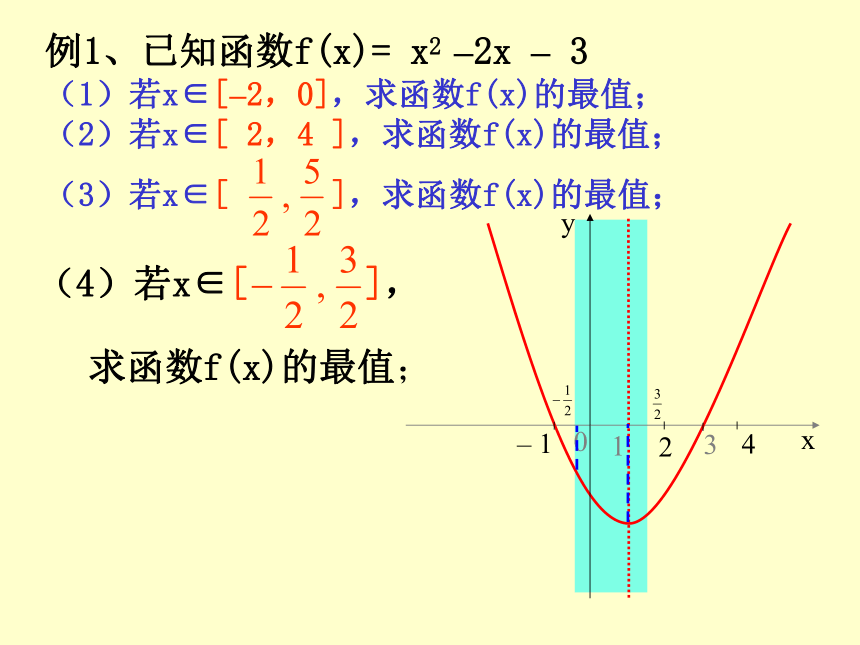
例1、已知函数f(x)= x2 –2x – 3.
(1)若x∈[ –2,0],求函数f(x)的最值;
(2)若x∈[ 2,4],求函数f(x)的最值;
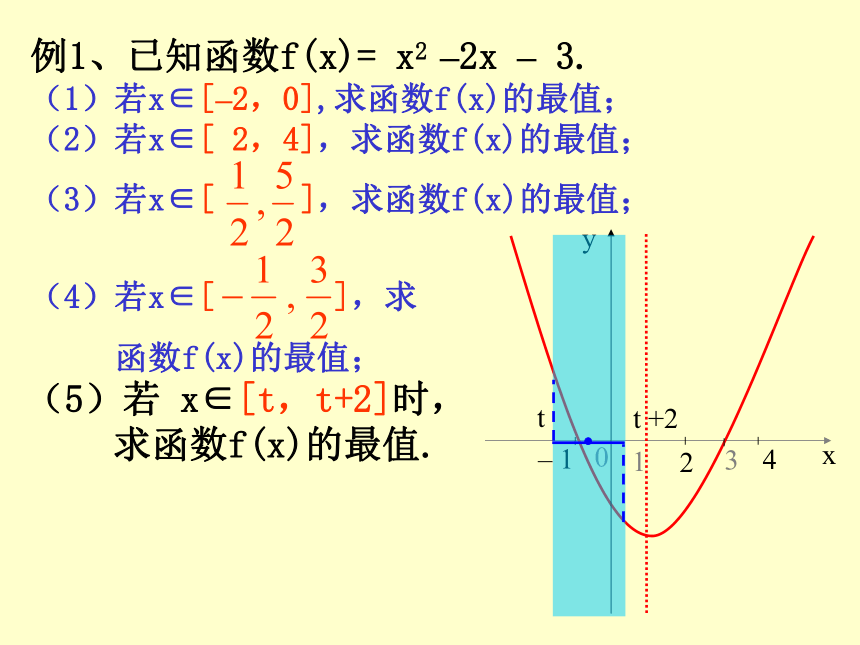
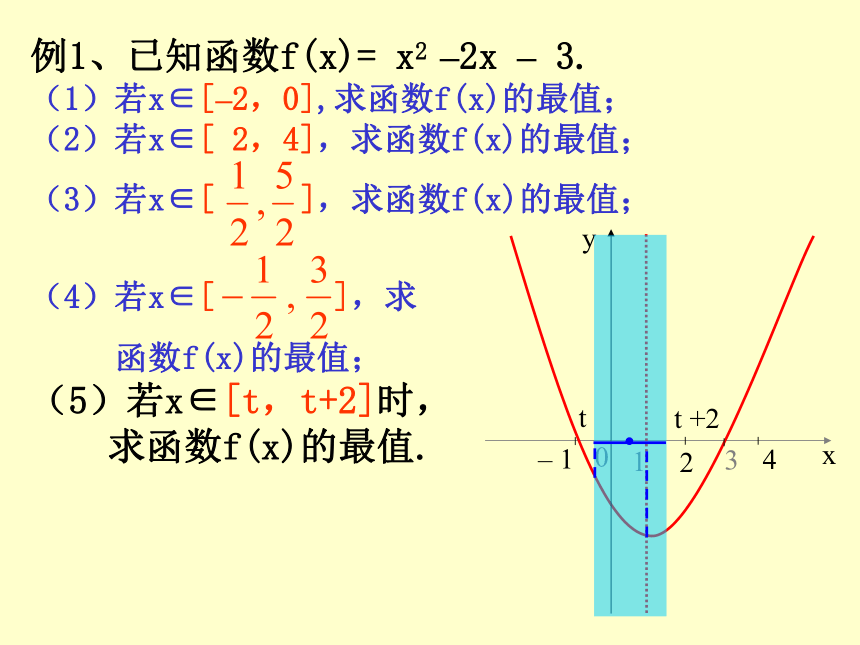
(5)若 x∈[t,t+2]时,
求函数f(x)的最值.
评注:例1属于“轴定区间变”的问题,看作动区间沿x轴移动的过程中,函数最值的变化,即动区间在定轴的左、右两侧及包含定轴的变化,要注意开口方向及端点情况。
轴动区间定时的值域与最值
简析:
简析:
解:②求函数y=x2-2ax+1,x∈[0,2]的最大值.
评注:例2属于“轴变区间定”的问题,看作对称轴沿x轴移动的过程中,函数最值的变化,即对称轴在定区间的左、右两侧及对称轴在定区间上变化情况,要注意开口方向及端点情况。
a>0
a<0
轴定,区间定,开口变
例3、求函数f(x)=ax2–2a2x+1(a≠0)在区间
[–1,2]上的最值.
例3、求函数f(x)=ax2–2a2x+1(a≠0)在区间
[–1,2]上的最值.
例3、求函数f(x)=ax2–2a2x+1(a≠0)在区间
[–1,2]上的最值.
例3、求函数f(x)=ax2–2a2x+1(a≠0)在区间
[–1,2]上的最值.
例3、求函数f(x)=ax2–2a2x+1(a≠0)在区间
[–1,2]上的最值.
例3、求函数f(x)=ax2–2a2x+1(a≠0)在区间
[–1,2]上的最值.
评注:例3属于“轴变区间定,开口变”的问题,看作对称轴沿x轴移动的过程中,函数最值的变化,即对称轴在定区间的左、右两侧及对称轴在定区间上变化情况,要注意开口方向及端点情况。
高中数学
例1、已知函数f(x)= x2–2x –3.
(1)若x∈[ –2,0 ], 求函数f(x)的最值;
轴定区间定时的值域与最值
例1、已知函数f(x)= x2 –2x – 3.
(1)若x∈[ –2,0 ],求函数f(x)的最值;
(2)若x∈[ 2,4 ],求函数f(x)的最值;
例1、已知函数f(x)= x2 –2x – 3.
(1)若x∈[ –2,0],求函数f(x)的最值;
(2)若x∈[ 2,4],求函数f(x)的最值;
(5)若 x∈[t,t+2]时,
求函数f(x)的最值.
评注:例1属于“轴定区间变”的问题,看作动区间沿x轴移动的过程中,函数最值的变化,即动区间在定轴的左、右两侧及包含定轴的变化,要注意开口方向及端点情况。
轴动区间定时的值域与最值
简析:
简析:
解:②求函数y=x2-2ax+1,x∈[0,2]的最大值.
评注:例2属于“轴变区间定”的问题,看作对称轴沿x轴移动的过程中,函数最值的变化,即对称轴在定区间的左、右两侧及对称轴在定区间上变化情况,要注意开口方向及端点情况。
a>0
a<0
轴定,区间定,开口变
例3、求函数f(x)=ax2–2a2x+1(a≠0)在区间
[–1,2]上的最值.
例3、求函数f(x)=ax2–2a2x+1(a≠0)在区间
[–1,2]上的最值.
例3、求函数f(x)=ax2–2a2x+1(a≠0)在区间
[–1,2]上的最值.
例3、求函数f(x)=ax2–2a2x+1(a≠0)在区间
[–1,2]上的最值.
例3、求函数f(x)=ax2–2a2x+1(a≠0)在区间
[–1,2]上的最值.
例3、求函数f(x)=ax2–2a2x+1(a≠0)在区间
[–1,2]上的最值.
评注:例3属于“轴变区间定,开口变”的问题,看作对称轴沿x轴移动的过程中,函数最值的变化,即对称轴在定区间的左、右两侧及对称轴在定区间上变化情况,要注意开口方向及端点情况。
