2.2用字母表示数量关系、公式、定律 课件(共21张ppt)
文档属性
| 名称 | 2.2用字母表示数量关系、公式、定律 课件(共21张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 350.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-01-17 00:00:00 | ||
图片预览





文档简介
课件15张PPT。加法结合律和交换律自主练习合作探索情境导入 冬青56棵,柳树72棵,杨树28棵。一、情境导入月季80棵,牡丹88棵,茶花112棵。 一共购进多少棵树苗? 一共购进多少棵花苗?从图中,你知道了哪些数学信息?根据这些信息,你能提出什么问题?
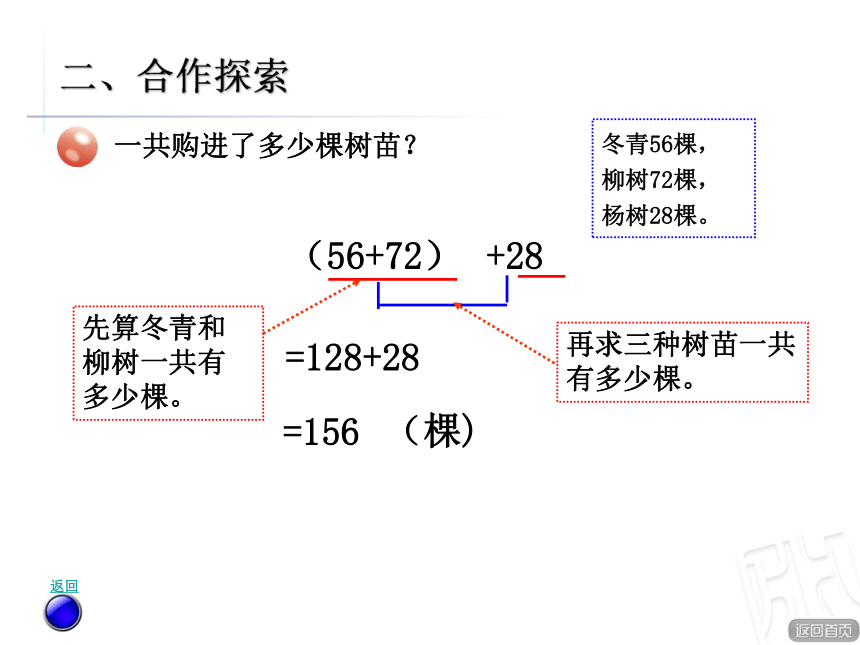
二、合作探索 后加先加想一想:1.要解决这个问题,可以先求什么,再求什么?2.你会列综合算式解答吗?一共购进了多少棵树苗? 等式 继续二、合作探索(56+72)=128+28=156(棵)+28 返回一共购进了多少棵树苗?冬青56棵,
柳树72棵,
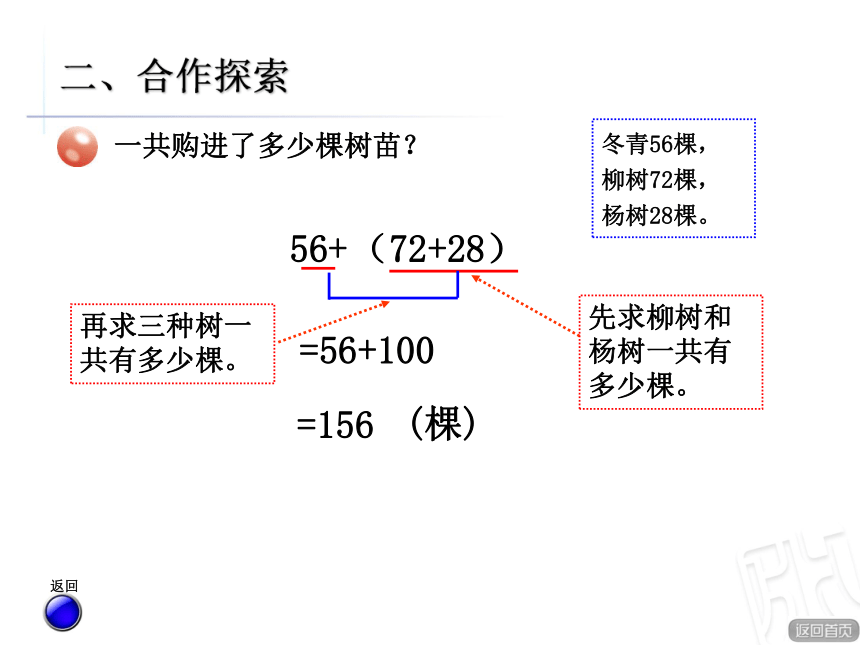
杨树28棵。(72+28)二、合作探索56+=56+100=156(棵) 返回一共购进了多少棵树苗?冬青56棵,
柳树72棵,
杨树28棵。二、合作探索56 +(72+28)(56+72)+28 56+(72+28)(56+ 72)+28 =你能把刚才这两道算式写成一个等式吗?= 156(棵)= 128+28= 56+100= 156(棵)二、合作探索80 +(88+112)(80+88)+112 80+(88+112)(80+ 88)+112 =你能把这两道算式写成一个等式吗? 方法二 方法一一共要购进多少棵花苗?月季80棵,
牡丹88棵,
茶花112棵。= 280(棵)= 168+112= 80+200= 280(棵) 问题 等式二、合作探索观察下面两组算式,你发现了什么? 三个数相加,先把前两个数相加,或者先把后两个数相加,和不变。这是不是一个规律呢?能举例验证一下吗?
二、合作探索+7523++1036137++217+7+29(29+21)23+5(5+75)137+64(64+1036)===二、合作探索(ɑ+b)+c=ɑ+(b+c)571237123710310357你会用字母表示吗? 三个数相加,先把前两个数相加,再与第三个数相加;
或者先把后两个数相加,再与第一个数相加,和不变。这个规律就是加法结合律。39+34 ○ 34+39 1210+790 ○ 790+1210 两个数相加,交换加数的位置,和不变。这个规律就是加法交换律。二、合作探索加法运算中还有其他的规律吗?(可用计算器计算)
34+2 ○ 2+34 3470+1210 ○ 1210+3470 ɑ+b ﹦b+ɑ﹦﹦﹦你发现了什么?363673734680468020002000﹦你会用字母表示吗?三、自主练习
1.下列算式运用哪些运算律。 85+0 = 0+85
47 +(33+8)=(47+33)+ 8
(94+68)+32 = 94+(68+32)
75+(48+25)=(75+25)+48
加法交换律加法结合律加法结合律加法交换律
加法结合律25+48加法交换律加法结合律三、自主练习
2.比一比,看一看。 (1) 8 7 6 1 5 0
+ 1 5 0 + 8 7 6 运用了加法( )律
交换 (2)7+9 =(6+1)+9 =6+(1+9) 运用了加法( )律
结合(3)6+7+4 = 7+(6+4)=17 运用了加法 ( )律
交换、 结合 验算采用“凑十法”计算,可以使计算简便。三、自主练习
3.在括号里填上合适的数。1273381604098274.先计算,再用加法交换律进行验算。
78+354=
三、自主练习 284+506=432790
二、合作探索 后加先加想一想:1.要解决这个问题,可以先求什么,再求什么?2.你会列综合算式解答吗?一共购进了多少棵树苗? 等式 继续二、合作探索(56+72)=128+28=156(棵)+28 返回一共购进了多少棵树苗?冬青56棵,
柳树72棵,
杨树28棵。(72+28)二、合作探索56+=56+100=156(棵) 返回一共购进了多少棵树苗?冬青56棵,
柳树72棵,
杨树28棵。二、合作探索56 +(72+28)(56+72)+28 56+(72+28)(56+ 72)+28 =你能把刚才这两道算式写成一个等式吗?= 156(棵)= 128+28= 56+100= 156(棵)二、合作探索80 +(88+112)(80+88)+112 80+(88+112)(80+ 88)+112 =你能把这两道算式写成一个等式吗? 方法二 方法一一共要购进多少棵花苗?月季80棵,
牡丹88棵,
茶花112棵。= 280(棵)= 168+112= 80+200= 280(棵) 问题 等式二、合作探索观察下面两组算式,你发现了什么? 三个数相加,先把前两个数相加,或者先把后两个数相加,和不变。这是不是一个规律呢?能举例验证一下吗?
二、合作探索+7523++1036137++217+7+29(29+21)23+5(5+75)137+64(64+1036)===二、合作探索(ɑ+b)+c=ɑ+(b+c)571237123710310357你会用字母表示吗? 三个数相加,先把前两个数相加,再与第三个数相加;
或者先把后两个数相加,再与第一个数相加,和不变。这个规律就是加法结合律。39+34 ○ 34+39 1210+790 ○ 790+1210 两个数相加,交换加数的位置,和不变。这个规律就是加法交换律。二、合作探索加法运算中还有其他的规律吗?(可用计算器计算)
34+2 ○ 2+34 3470+1210 ○ 1210+3470 ɑ+b ﹦b+ɑ﹦﹦﹦你发现了什么?363673734680468020002000﹦你会用字母表示吗?三、自主练习
1.下列算式运用哪些运算律。 85+0 = 0+85
47 +(33+8)=(47+33)+ 8
(94+68)+32 = 94+(68+32)
75+(48+25)=(75+25)+48
加法交换律加法结合律加法结合律加法交换律
加法结合律25+48加法交换律加法结合律三、自主练习
2.比一比,看一看。 (1) 8 7 6 1 5 0
+ 1 5 0 + 8 7 6 运用了加法( )律
交换 (2)7+9 =(6+1)+9 =6+(1+9) 运用了加法( )律
结合(3)6+7+4 = 7+(6+4)=17 运用了加法 ( )律
交换、 结合 验算采用“凑十法”计算,可以使计算简便。三、自主练习
3.在括号里填上合适的数。1273381604098274.先计算,再用加法交换律进行验算。
78+354=
三、自主练习 284+506=432790
