七年级数学下册5.1相交线助学案(含4课时,无答案)
文档属性
| 名称 | 七年级数学下册5.1相交线助学案(含4课时,无答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 133.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-01-17 20:12:29 | ||
图片预览


文档简介
课题 5.1相交线 课型 新授 主备
审核 班级 姓名 时间
助学 目标 1、知道对顶角、邻补角的定义,找出图形中一个角的对顶角和邻补角. 2、经历探索“对顶角相等”的性质,并会进行有关的简单推理和计算.3、激情参与,全力以赴,主动发现,通过合作学习享受成功的快乐
重点 邻补角和对顶角的概念及对顶角相等的性质
难点 写出规范的推理过程和对对顶角相等的探索
学习过程 学(教)记录
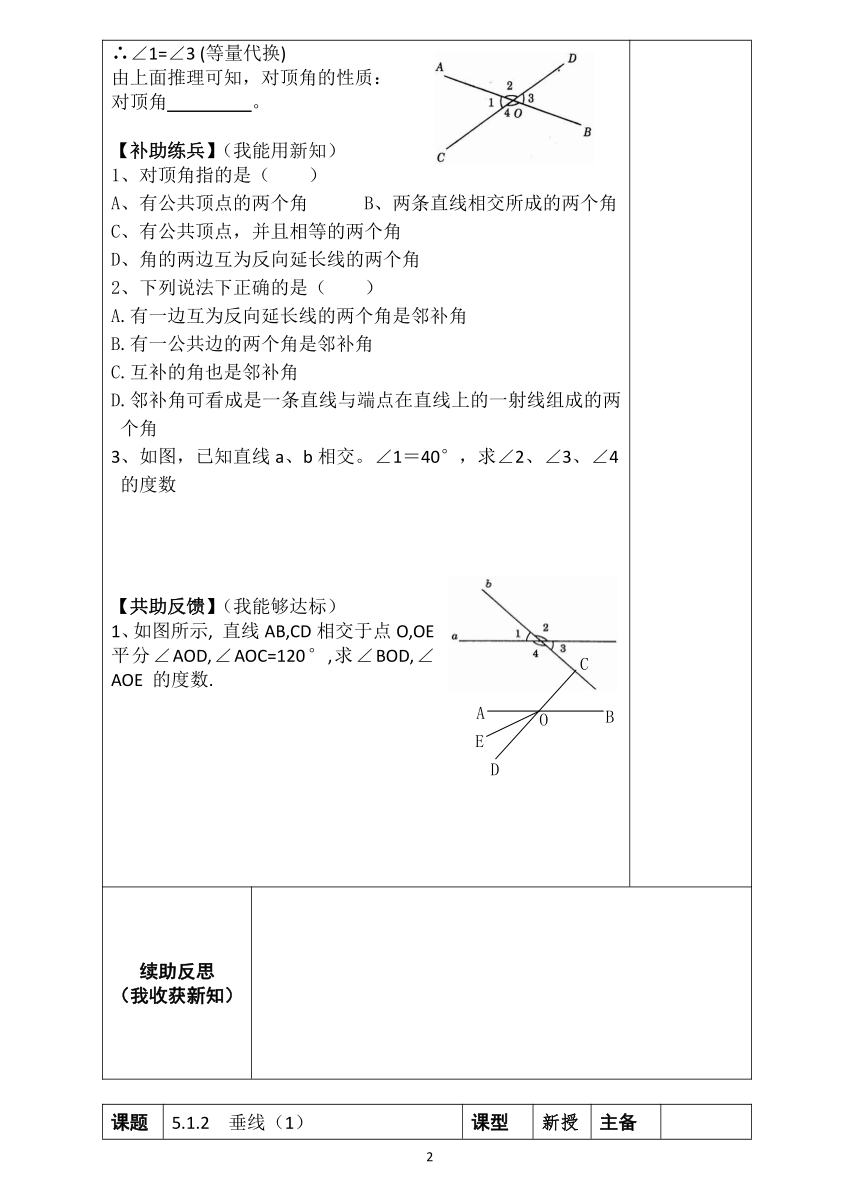
【自助学习】(我尝试自学) 1、填空:①两个角的和是 ,这样的两个角叫做互为补角,即其中一个角是另一个角的补角。 ②同角或 的补角 。 2、邻补角、对顶角 观察思考:剪刀剪开纸张的过程,随着两个把手之间的角逐渐变小,剪刀刃之间的角度也相应 。我们把剪刀的构成抽象为两条直线,就是我们要研究的两条相交直线所成的角的问题。 【互助探究】(我参与互研)(一)邻补角、对顶角 探索活动:1、①任意画两条相交直线,在形成的四个角(∠1,∠2,∠3,∠4)中,两两相配共能组成 对角。分别是 。 ②分别测量一下各个角的度数,是否发现规律?你能否把他们分类? ③再画两条相交直线比较。 归纳:邻补角、对顶角定义 【求助交流】(我愿意分享)(二)邻补角、对顶角的性质 1、邻补角的性质:邻补角 。 注意:邻补角是互补的一种特殊的情况,数量上 ,位置上有一条 。 2、对顶角的性质:完成推理过程 如图,∵∠1+∠2 = ,∠2+∠3 = 。(邻补角定义) ∴∠1=180°- ,∠3 =180°- (等式性质)∴∠1=∠3 (等量代换) 由上面推理可知,对顶角的性质: 对顶角 。 【补助练兵】(我能用新知) 1、对顶角指的是( ) A、有公共顶点的两个角 B、两条直线相交所成的两个角 C、有公共顶点,并且相等的两个角 D、角的两边互为反向延长线的两个角 2、下列说法下正确的是( ) A.有一边互为反向延长线的两个角是邻补角 B.有一公共边的两个角是邻补角 C.互补的角也是邻补角 D.邻补角可看成是一条直线与端点在直线上的一射线组成的两个角3、如图,已知直线a、b相交。∠1=40°,求∠2、∠3、∠4的度数 【共助反馈】(我能够达标)1、如图所示, 直线AB,CD相交于点O,OE平分∠AOD,∠AOC=120°,求∠BOD,∠AOE的度数.
续助反思 (我收获新知)
课题 5.1.2 垂线(1) 课型 新授 主备
审核 班级 姓名 时间
助学 目标 1、理解垂线、垂线段的概念,会用三角尺或量角器过一点画已知直线的垂线。掌握垂线的性质,并会利用所学知识进行简单的推理。 2、经历观察、操作、想像、归纳概括、交流等活动,进一步发展空间观念, 培养学生用几何语言准确表达的能力。毛 3、探索并了解垂线的一些性质,感悟实践出真知的哲理性
重点 垂线的定义及性质。
难点 垂线的画法
学习过程 学(教)记录
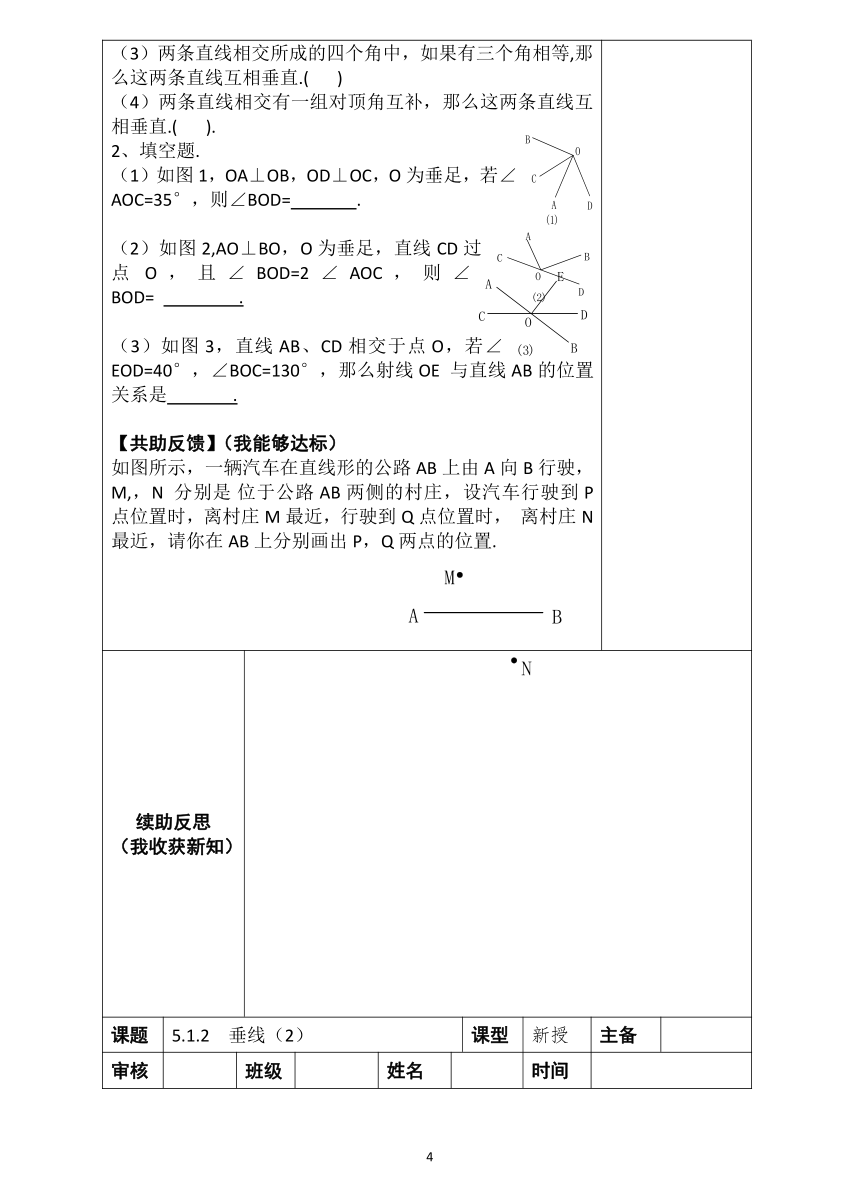
【自助学习】(我尝试自学)1.如图,若∠1=60°,那么∠2= 、∠3= 、 ∠4= 2.改变上图中∠1的大小,若∠1=90°,请画出这种图形,并求出此时∠2、∠3、∠4的大小。 3、两条直线相交,所成四个角中有一个角是 时,我们称这两条直线 其中一条直线是另一条的 ,他们的交点叫做 。【互助探究】(我参与互研)1、垂直的表示方法:垂直用符号“⊥”来表示,若“直线AB垂直于直线CD, 垂足为O”,则记为 ,并在图中任意一个角处作上直角记号,如下图。 3、用三角尺或量角器画已知直线L的垂线. (1)已知直线L,画出直线L的垂线,能画几条? (2)经过直线l上一点A画该直线的垂线,能画几条? (3)经过直线l外一点B画该直线的垂线,能画几条? 【求助交流】(我愿意分享)已知钝角∠AOB,点D在射线OB上. (1)画直线DE⊥OB (2)画直线DF⊥OA,垂足为F. 【补助练兵】(我能用新知)1、判断题. (1)两条直线互相垂直,则所有的邻补角都相等.( ) (2)一条直线不可能与两条相交直线都垂直.( ) (3)两条直线相交所成的四个角中,如果有三个角相等,那么这两条直线互相垂直.( )(4)两条直线相交有一组对顶角互补,那么这两条直线互相垂直.( ). 2、填空题. (1)如图1,OA⊥OB,OD⊥OC,O为垂足,若∠AOC=35°,则∠BOD= . (2)如图2,AO⊥BO,O为垂足,直线CD过点O,且∠BOD=2∠AOC,则∠BOD= . (3)如图3,直线AB、CD相交于点O,若∠EOD=40°,∠BOC=130°,那么射线OE 与直线AB的位置关系是 .【共助反馈】(我能够达标)如图所示,一辆汽车在直线形的公路AB上由A向B行驶,M,,N分别是?位于公路AB两侧的村庄,设汽车行驶到P点位置时,离村庄M最近,行驶到Q点位置时,离村庄N最近,请你在AB上分别画出P,Q两点的位置.
续助反思 (我收获新知)
课题 5.1.2 垂线(2) 课型 新授 主备
审核 班级 姓名 时间
助学 目标 1、了解垂线段的概念,了解垂线段最短的性质,体会点到直线的距离的意义, 并会度量点到直线的距离。 2、经历观察、操作、想像、归纳概括、交流等活动,进一步发展空间观念, 培养学生用几何语言准确表达的能力。 3、探索并了解垂线的一些性质,感悟实践出真知的哲理性
重点 “垂线段最短”的性质,点到直线的距离的概念及其简单应用。
难点 对点到直线的距离的概念的理解。
学习过程 学(教)记录
【自助学习】(我尝试自学)1、上学期我们学习过“什么什么最短”的几何知识,还记得吗? 2、 如图所示,村庄A要从河流L引水入庄,需修筑一水渠,请你画出修筑水渠的路线图。【互助探究】(我参与互研)1、问题转化 如果把小河看成是直线L,把要挖的渠道看成是一条线段,则该线段的一个端点自然是农田A,另一个端点就是直线L上的某个点。那么最短渠道问题会变成是怎样的数学问题? 2、画图验证 (1)画直线L,在L外取一点P; (2)过P点出PO⊥L,垂足为O; (3)点A1,A2,A3……在L上,连接PA、PA2、PA3……; (4)用度量法比较线段PO、PA1、PA2、PA3……的大小,.得出线段 最小。 3、归纳结论: 连接直线外一点与直线上各点的所有线段中, .简单说成: .4、知识类比 (1)垂线段与垂线有何区别联系? (2)垂线段与线段有何区别与联系?【求助交流】(我愿意分享)1、判断对错,并说明理由:. (1)直线外一点与直线上的一点间的线段的长度是这一点到这条直线的距离。( )(2)如图,线段AE是点A到直线BC的距离。( ) (3)如图,线段CD的长是点C到直线AB的距离。( ) 2、已知直线a、b,过点a上一点A作AB⊥a,交b于点B,过B作BC⊥b交a于点C.请说出哪一条线段的长是哪一点到哪一条直线的距离? 并且用刻度尺测量这个距离. 【补助练兵】(我能用新知) 1、如图,AC⊥BC,C为垂足,CD⊥AB,D为垂足,BC=8,CD=4.8,BD=6.4,AD=3.6,AC= 6,那么点C到AB的距离是 ,点A到BC的距离是 ,点B到CD 的距离是 ,A、B两点的距离是 2.如图,在线段AB、AC、AD、AE、AF中AD最短.小明说垂线段最短, 因此线段AD的长是点A到BF的距离,对小明的说法,你认为对吗? 【共助反馈】(我能够达标)用三角尺画一个是30°的∠AOB,在边OA上任取一点P,过P作PQ⊥OB, 垂足为Q,量一量OP的长,你发现点P到OB的距离与OP长的关系吗?
续助反思 (我收获新知)
课题 5.1.3同位角、内错角、同旁内角 课型 新授 主备
审核 班级 姓名 时间
助学 目标 1、了解同位角、内错角、同旁内角的概念。 2、会识别同位角、内错角、同旁内角的概念。 3、在活动中培养乐于探索、合作学习的习惯,培养学生“用数学”的 意识和能力。
重点 同位角、内错角、同旁内角的识别。
难点 已知两个角,要判别是哪两条直线被第三条直线所截而形成的什么关系的角。
学习过程 学(教)记录
【自助学习】(我尝试自学)1.指出右图中所有的邻补角和对顶角? 2. 图中的∠1与∠5,∠3与∠5,∠3与∠6 是邻补角或对顶角吗?若都不是,它们各是什么关系的角?【互助探究】(我参与互研)如图,直线AB、CD与EF相交(或两条直线AB、CD被第三条直线EF所截)构成 个角。 我们来研究其中没有公共顶点的两个角的关系。 (一)同位角 1、如图1,∠1和∠5,分别在直线AB、CD的 ,在直线EF的 。具有这种位置关系的一对角叫同位角。 2、请你找出图中还有哪几对角构成同位角。 3、两条直线被第三条直线所截构成的八个角中,共有 对同位角。 (二)内错角 1、如上图,∠3和∠5,分别在直线AB、CD的 , 在直线EF的 。具有这种位置关系的一对角叫做内错角。 2、请你找出图中还有哪几对角构成内错角。 3、两条直线被第三条直线所截构成的八个角中共有 对内错角 (三)同旁内角 1、如上图,∠3和∠6,分别在直线AB、CD的 ,在直线EF的 。具有这种位置关系的一对角叫做同旁内角。 2、请你找出图中还有哪几对角构成同旁内角。 3、两条直线被第三条直线所截构成的八个角中,共有 对同旁内角【求助交流】(我愿意分享)说出下列各对角是哪两条直线被哪一条直线所截而得到的什么角? ∠1与∠2 ,∠1与∠3 ,∠3与∠4 , ∠2与∠4 ,∠5与∠8 ,∠5与∠7 , ∠6与∠7 ,∠6与∠8 【补助练兵】(我能用新知)1、如图,直线 、 被 所截,∠1与∠2是内错角,直线 、 被 所截,∠1与∠B是同位角; 直线 、 被 所截,∠3和∠B是同位角。 2、如右图(6)所示: (1)∠1,∠2,∠3,∠4,∠5,∠6是直线 、 被第三条直线 所截而成的。(2)∠2的同位角是 ,∠1的同位角是 。 (3)∠3的内错角是 ,∠4的内错角是 。 (4)∠6的同旁内角是 ,∠5的同旁内角是 (5)∠4与∠A是同旁内角吗?为什么?【共助反馈】(我能够达标)如图⑺,在直角ABC中,∠C=90°,DE⊥AC于E,交AB于D .①指出当BC、DE被AB所截时,∠3的同位角、内错角和同旁内角。②试说明∠1=∠2=∠3的理由.(提示:三角形内角和是1800
续助反思 (我收获新知)
A
B
C
D
5
7
6
8
A
B
C
E
F
1
3
4
5
6
2
PAGE
7
审核 班级 姓名 时间
助学 目标 1、知道对顶角、邻补角的定义,找出图形中一个角的对顶角和邻补角. 2、经历探索“对顶角相等”的性质,并会进行有关的简单推理和计算.3、激情参与,全力以赴,主动发现,通过合作学习享受成功的快乐
重点 邻补角和对顶角的概念及对顶角相等的性质
难点 写出规范的推理过程和对对顶角相等的探索
学习过程 学(教)记录
【自助学习】(我尝试自学) 1、填空:①两个角的和是 ,这样的两个角叫做互为补角,即其中一个角是另一个角的补角。 ②同角或 的补角 。 2、邻补角、对顶角 观察思考:剪刀剪开纸张的过程,随着两个把手之间的角逐渐变小,剪刀刃之间的角度也相应 。我们把剪刀的构成抽象为两条直线,就是我们要研究的两条相交直线所成的角的问题。 【互助探究】(我参与互研)(一)邻补角、对顶角 探索活动:1、①任意画两条相交直线,在形成的四个角(∠1,∠2,∠3,∠4)中,两两相配共能组成 对角。分别是 。 ②分别测量一下各个角的度数,是否发现规律?你能否把他们分类? ③再画两条相交直线比较。 归纳:邻补角、对顶角定义 【求助交流】(我愿意分享)(二)邻补角、对顶角的性质 1、邻补角的性质:邻补角 。 注意:邻补角是互补的一种特殊的情况,数量上 ,位置上有一条 。 2、对顶角的性质:完成推理过程 如图,∵∠1+∠2 = ,∠2+∠3 = 。(邻补角定义) ∴∠1=180°- ,∠3 =180°- (等式性质)∴∠1=∠3 (等量代换) 由上面推理可知,对顶角的性质: 对顶角 。 【补助练兵】(我能用新知) 1、对顶角指的是( ) A、有公共顶点的两个角 B、两条直线相交所成的两个角 C、有公共顶点,并且相等的两个角 D、角的两边互为反向延长线的两个角 2、下列说法下正确的是( ) A.有一边互为反向延长线的两个角是邻补角 B.有一公共边的两个角是邻补角 C.互补的角也是邻补角 D.邻补角可看成是一条直线与端点在直线上的一射线组成的两个角3、如图,已知直线a、b相交。∠1=40°,求∠2、∠3、∠4的度数 【共助反馈】(我能够达标)1、如图所示, 直线AB,CD相交于点O,OE平分∠AOD,∠AOC=120°,求∠BOD,∠AOE的度数.
续助反思 (我收获新知)
课题 5.1.2 垂线(1) 课型 新授 主备
审核 班级 姓名 时间
助学 目标 1、理解垂线、垂线段的概念,会用三角尺或量角器过一点画已知直线的垂线。掌握垂线的性质,并会利用所学知识进行简单的推理。 2、经历观察、操作、想像、归纳概括、交流等活动,进一步发展空间观念, 培养学生用几何语言准确表达的能力。毛 3、探索并了解垂线的一些性质,感悟实践出真知的哲理性
重点 垂线的定义及性质。
难点 垂线的画法
学习过程 学(教)记录
【自助学习】(我尝试自学)1.如图,若∠1=60°,那么∠2= 、∠3= 、 ∠4= 2.改变上图中∠1的大小,若∠1=90°,请画出这种图形,并求出此时∠2、∠3、∠4的大小。 3、两条直线相交,所成四个角中有一个角是 时,我们称这两条直线 其中一条直线是另一条的 ,他们的交点叫做 。【互助探究】(我参与互研)1、垂直的表示方法:垂直用符号“⊥”来表示,若“直线AB垂直于直线CD, 垂足为O”,则记为 ,并在图中任意一个角处作上直角记号,如下图。 3、用三角尺或量角器画已知直线L的垂线. (1)已知直线L,画出直线L的垂线,能画几条? (2)经过直线l上一点A画该直线的垂线,能画几条? (3)经过直线l外一点B画该直线的垂线,能画几条? 【求助交流】(我愿意分享)已知钝角∠AOB,点D在射线OB上. (1)画直线DE⊥OB (2)画直线DF⊥OA,垂足为F. 【补助练兵】(我能用新知)1、判断题. (1)两条直线互相垂直,则所有的邻补角都相等.( ) (2)一条直线不可能与两条相交直线都垂直.( ) (3)两条直线相交所成的四个角中,如果有三个角相等,那么这两条直线互相垂直.( )(4)两条直线相交有一组对顶角互补,那么这两条直线互相垂直.( ). 2、填空题. (1)如图1,OA⊥OB,OD⊥OC,O为垂足,若∠AOC=35°,则∠BOD= . (2)如图2,AO⊥BO,O为垂足,直线CD过点O,且∠BOD=2∠AOC,则∠BOD= . (3)如图3,直线AB、CD相交于点O,若∠EOD=40°,∠BOC=130°,那么射线OE 与直线AB的位置关系是 .【共助反馈】(我能够达标)如图所示,一辆汽车在直线形的公路AB上由A向B行驶,M,,N分别是?位于公路AB两侧的村庄,设汽车行驶到P点位置时,离村庄M最近,行驶到Q点位置时,离村庄N最近,请你在AB上分别画出P,Q两点的位置.
续助反思 (我收获新知)
课题 5.1.2 垂线(2) 课型 新授 主备
审核 班级 姓名 时间
助学 目标 1、了解垂线段的概念,了解垂线段最短的性质,体会点到直线的距离的意义, 并会度量点到直线的距离。 2、经历观察、操作、想像、归纳概括、交流等活动,进一步发展空间观念, 培养学生用几何语言准确表达的能力。 3、探索并了解垂线的一些性质,感悟实践出真知的哲理性
重点 “垂线段最短”的性质,点到直线的距离的概念及其简单应用。
难点 对点到直线的距离的概念的理解。
学习过程 学(教)记录
【自助学习】(我尝试自学)1、上学期我们学习过“什么什么最短”的几何知识,还记得吗? 2、 如图所示,村庄A要从河流L引水入庄,需修筑一水渠,请你画出修筑水渠的路线图。【互助探究】(我参与互研)1、问题转化 如果把小河看成是直线L,把要挖的渠道看成是一条线段,则该线段的一个端点自然是农田A,另一个端点就是直线L上的某个点。那么最短渠道问题会变成是怎样的数学问题? 2、画图验证 (1)画直线L,在L外取一点P; (2)过P点出PO⊥L,垂足为O; (3)点A1,A2,A3……在L上,连接PA、PA2、PA3……; (4)用度量法比较线段PO、PA1、PA2、PA3……的大小,.得出线段 最小。 3、归纳结论: 连接直线外一点与直线上各点的所有线段中, .简单说成: .4、知识类比 (1)垂线段与垂线有何区别联系? (2)垂线段与线段有何区别与联系?【求助交流】(我愿意分享)1、判断对错,并说明理由:. (1)直线外一点与直线上的一点间的线段的长度是这一点到这条直线的距离。( )(2)如图,线段AE是点A到直线BC的距离。( ) (3)如图,线段CD的长是点C到直线AB的距离。( ) 2、已知直线a、b,过点a上一点A作AB⊥a,交b于点B,过B作BC⊥b交a于点C.请说出哪一条线段的长是哪一点到哪一条直线的距离? 并且用刻度尺测量这个距离. 【补助练兵】(我能用新知) 1、如图,AC⊥BC,C为垂足,CD⊥AB,D为垂足,BC=8,CD=4.8,BD=6.4,AD=3.6,AC= 6,那么点C到AB的距离是 ,点A到BC的距离是 ,点B到CD 的距离是 ,A、B两点的距离是 2.如图,在线段AB、AC、AD、AE、AF中AD最短.小明说垂线段最短, 因此线段AD的长是点A到BF的距离,对小明的说法,你认为对吗? 【共助反馈】(我能够达标)用三角尺画一个是30°的∠AOB,在边OA上任取一点P,过P作PQ⊥OB, 垂足为Q,量一量OP的长,你发现点P到OB的距离与OP长的关系吗?
续助反思 (我收获新知)
课题 5.1.3同位角、内错角、同旁内角 课型 新授 主备
审核 班级 姓名 时间
助学 目标 1、了解同位角、内错角、同旁内角的概念。 2、会识别同位角、内错角、同旁内角的概念。 3、在活动中培养乐于探索、合作学习的习惯,培养学生“用数学”的 意识和能力。
重点 同位角、内错角、同旁内角的识别。
难点 已知两个角,要判别是哪两条直线被第三条直线所截而形成的什么关系的角。
学习过程 学(教)记录
【自助学习】(我尝试自学)1.指出右图中所有的邻补角和对顶角? 2. 图中的∠1与∠5,∠3与∠5,∠3与∠6 是邻补角或对顶角吗?若都不是,它们各是什么关系的角?【互助探究】(我参与互研)如图,直线AB、CD与EF相交(或两条直线AB、CD被第三条直线EF所截)构成 个角。 我们来研究其中没有公共顶点的两个角的关系。 (一)同位角 1、如图1,∠1和∠5,分别在直线AB、CD的 ,在直线EF的 。具有这种位置关系的一对角叫同位角。 2、请你找出图中还有哪几对角构成同位角。 3、两条直线被第三条直线所截构成的八个角中,共有 对同位角。 (二)内错角 1、如上图,∠3和∠5,分别在直线AB、CD的 , 在直线EF的 。具有这种位置关系的一对角叫做内错角。 2、请你找出图中还有哪几对角构成内错角。 3、两条直线被第三条直线所截构成的八个角中共有 对内错角 (三)同旁内角 1、如上图,∠3和∠6,分别在直线AB、CD的 ,在直线EF的 。具有这种位置关系的一对角叫做同旁内角。 2、请你找出图中还有哪几对角构成同旁内角。 3、两条直线被第三条直线所截构成的八个角中,共有 对同旁内角【求助交流】(我愿意分享)说出下列各对角是哪两条直线被哪一条直线所截而得到的什么角? ∠1与∠2 ,∠1与∠3 ,∠3与∠4 , ∠2与∠4 ,∠5与∠8 ,∠5与∠7 , ∠6与∠7 ,∠6与∠8 【补助练兵】(我能用新知)1、如图,直线 、 被 所截,∠1与∠2是内错角,直线 、 被 所截,∠1与∠B是同位角; 直线 、 被 所截,∠3和∠B是同位角。 2、如右图(6)所示: (1)∠1,∠2,∠3,∠4,∠5,∠6是直线 、 被第三条直线 所截而成的。(2)∠2的同位角是 ,∠1的同位角是 。 (3)∠3的内错角是 ,∠4的内错角是 。 (4)∠6的同旁内角是 ,∠5的同旁内角是 (5)∠4与∠A是同旁内角吗?为什么?【共助反馈】(我能够达标)如图⑺,在直角ABC中,∠C=90°,DE⊥AC于E,交AB于D .①指出当BC、DE被AB所截时,∠3的同位角、内错角和同旁内角。②试说明∠1=∠2=∠3的理由.(提示:三角形内角和是1800
续助反思 (我收获新知)
A
B
C
D
5
7
6
8
A
B
C
E
F
1
3
4
5
6
2
PAGE
7
