2018-2019学年江苏省镇江市高二(上)期中数学试卷(解析版)
文档属性
| 名称 | 2018-2019学年江苏省镇江市高二(上)期中数学试卷(解析版) |  | |
| 格式 | zip | ||
| 文件大小 | 240.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-01-17 20:05:14 | ||
图片预览




文档简介
2018-2019学年江苏省镇江市高二(上)期中数学试卷
一、填空题(本大题共14小题,共56.0分)
抛物线y2=6x的准线方程为______.
直角梯形绕着它的垂直于底边的腰所在的直线旋转一周,形成的几何体是______.
已知圆锥底面半径为1,高为
3
,则该圆锥的侧面积为______.
圆C1:x2+y2+2x+2y=0和圆C2:x2+y2-6x+2y+6=0的公切线有______.
已知正四棱锥的侧面积为4
2
,底面边长为2,则该四棱锥的体积______
已知抛物线y2=8x的焦点是双曲线
??
2
??
2
?
??
2
3
=1(??>0)的右焦点,则双曲线的渐近线方程为______.
已知l,m是两条不同的直线,α,β,γ是三个不同的平面,在下列给出的4个命题中,所有真命题的序号为______ ①l⊥α,m?α?l⊥m ②l∥α,m?α?l∥m ③α⊥β,α⊥γ?β∥γ ④α⊥β,l⊥β?l∥α
已知地球表面及约是火星表面积的4倍,则地球体积是火星体积的______.
若抛物线y2=2x上的一点M到坐标原点O的距离为
3
,则点M到该抛物线焦点的距离为______.
双曲线C1:
??
2
??
2
?
??
2
??
2
=1(a>0,b>0)的左右焦点分别为F1,F2,过F1作一条直线l交双曲线右支于点P,PF2⊥x轴,且sin∠PF1F2=
1
3
,则双曲线的离心率为______
椭圆
??
2
??
2
+
??
2
??
2
=1(a>b>0)的上顶点为B,左焦点为F,直线BF与直线x+y-3
2
=0垂直,垂足为M,且点B为线段MF的中点,该椭圆方程为______.
已知圆柱M的底面半径为2,高为
2
3
3
,圆锥N的底面直径和母线长相等,若圆柱M?和圆锥N的体积相同,则圆锥N的底面半径为______.
如图,在正方体ABCD-A1B1C1D1中,点P在面对角线AC上运动,给出下列四个命题: ①D1P∥平面A1BC1;? ②D1P⊥BD; ③平面PDB1⊥平面A1BC1; ④三棱锥A1-BPC1的体积不变. 则其中所有正确的命题的序号是______.
已知椭圆
??
2
4
+
??
2
3
=1的左、右顶点分别为A,B,直线l斜率大于0,且l经过椭圆的右焦点F,与椭圆交于两点P,Q,若△AFP,△BFQ的面积分别为S1,S2,若
??
1
??
2
=
3
2
,则直线l的斜率为______.
二、解答题(本大题共6小题,共94.0分)
如图,在直三棱柱ABC-A1B1C1中,D,E分别为棱AB,BC的中点,点F在侧棱B1B上,且B1E⊥C1F,A1C1⊥B1C1. (1)求证:DE∥平面A1C1F; (2)求证:B1E⊥平面A1C1F
如图,四棱锥P-ABCD的底面为矩形,侧棱PA⊥底面ABCD,且PA=AD,E,F分别是线段PA,PD的中点,H在线段AB上. (1)求证:PC⊥AF; (2)若平面PBC∥平面EFH,求证H是AB的中点; (3)若AD=4,AB=2,求点D到平面PAC的距离.
已知圆M的方程为x2+(y-2)2=1,直线l的方程为x-2y=0,点P在直线l上,过点P作圆M的切线PA,PB,切点为A,B. (1)若点P的横坐标为1,求切线PA,PB的方程; (2)若点P的纵坐标为a,且在圆M上存在点Q到点P的距离为1,求实数a的取值范围.
在某海礁A处有一风暴中心,距离风暴中心A正东方向200km的B处有一艘轮船,正以北偏西a(a为锐角)角方向航行,速度为40km/h.已知距离风暴中心180km以内的水域受其影响. (1)若轮船不被风暴影响,求角α的正切值的最大值? (2)若轮船航行方向为北偏西45°,求轮船被风暴影响持续多少时间?
已知椭圆E:
??
2
??
2
+
??
2
??
2
=1(a>b>0)的焦距为2
3
,一条准线方程为x=
4
3
3
,A,B分别为椭圆的右顶点和上顶点,点P,Q在的椭圆上,且点P在第一象限. (1)求椭圆E的标准方程; (2)若点P,Q关于坐标原点对称,且PQ⊥AB,求四边形ABCD的面积; (3)若AP,BQ的斜率互为相反数,求证:PQ斜率为定值.
如图,在平面直角坐标系xoy中,F为椭圆E:
??
2
6
+
??
2
2
=1的右焦点,过F作两条相互垂直的直线AB,CD,与椭圆E分别交于A,B和点C,D. (1)当AB=
5
7
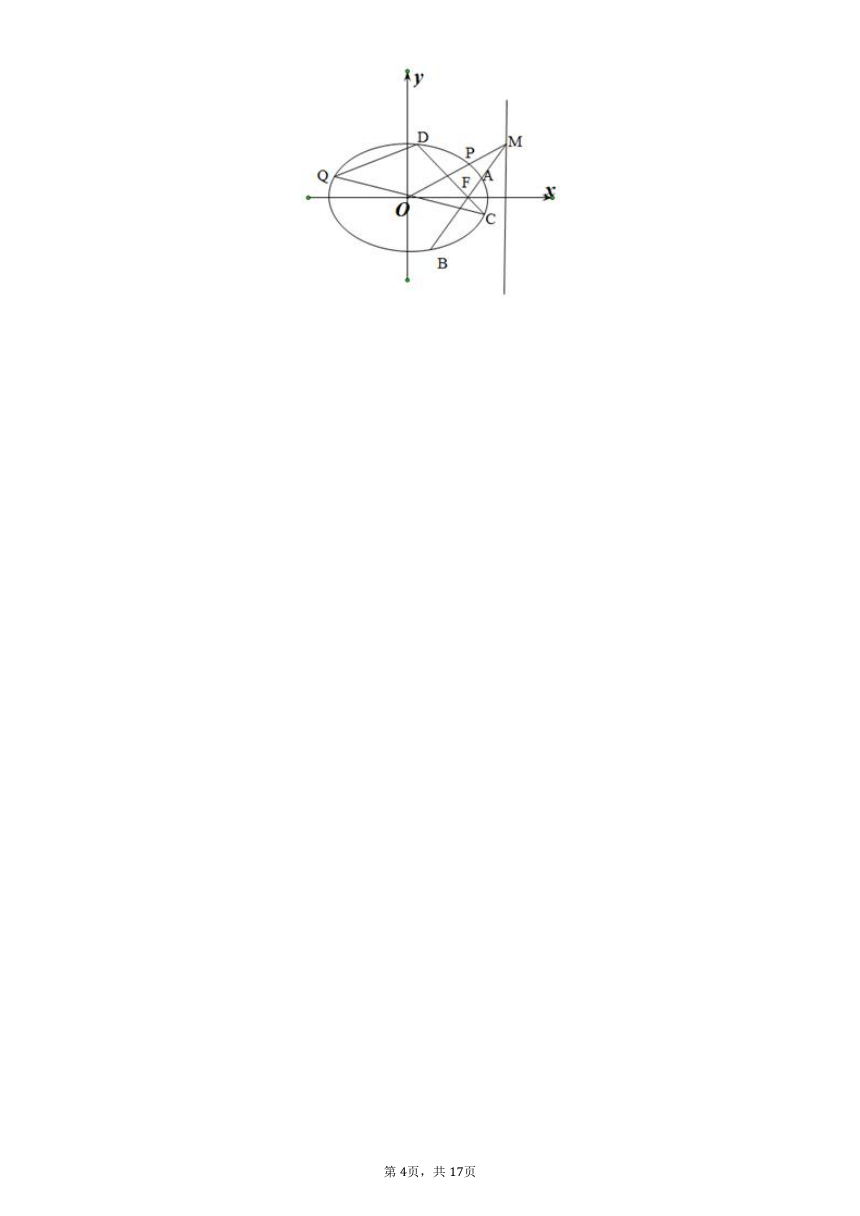
????时,求直线AB的方程; (2)直线AB交直线x=3于点M,OM与CD交于P,CO与椭圆E交于Q,求证:OM∥DQ.
答案和解析
1.【答案】x=-
3
2
【解析】
解:抛物线方程可知p=3, ∴准线方程为x=-=- 故答案为x=- 根据抛物线方程求得p,进而根据抛物线性质求得其准线方程. 本题主要考查了抛物线的简单性质.属基础题.
2.【答案】圆台 【解析】
解:由圆台的结构特征,可知直角梯形绕着它的垂直于底边的腰所在的直线旋转一周, 形成的几何体是圆台. 故答案为:圆台. 直接由圆台的结构特征得答案. 本题考查圆台的结构特征,是基础题.
3.【答案】2π 【解析】
解:由已知可得r=1,h=,则圆锥的母线长l=. ∴圆锥的侧面积S=πrl=2π. 故答案为:2π. 由已知求得母线长,代入圆锥侧面积公式求解. 本题考查圆锥侧面积的求法,关键是对公式的记忆,是基础题.
4.【答案】4 【解析】
解:根据题意,圆C1:x2+y2+2x+2y=0的标准方程为(x+1)2+(y+1)2=2,其圆心坐标为C1(-1,-1),半径R=, 圆C2:x2+y2-6x+2y+6=0的标准方程为(x-3)2+(y+1)2=4,其圆心坐标为C2(3,-1),半径r=2, 圆心距离C1C2=3-(-1)=4>2+, 即两圆相外离,则公切线有4条, 故答案为:4 根据题意,将两圆的方程变形为标准方程,求出圆心的坐标以及半径,分析两圆的位置关系,即可得答案. 本题主要考查两圆公切线的条数,判断两圆的位置关系是解决本题的关键.
5.【答案】
4
3
【解析】
解:顶点P在底面的射影是正方形ABCD的中心,如图所示; 正四棱锥的侧面积为S侧面=4??2?PE=4, ∴PE=, ∴该正四棱锥的高长度为: OP===1. 所以棱锥的体积为:=. 故答案为:. 根据题意知顶点在底面的射影是正方形的中心,利用侧面积求出斜高,再计算正四棱锥的高,然后求解体积. 本题考查了正四棱锥的结构特征与应用问题,根据棱锥的侧面求斜高是解题的关键.
6.【答案】??=±
3
?? 【解析】
解:∵抛物线方程为y2=8x, ∴2p=8,=2,可得抛物线的焦点为F(2,0). ∵抛物线y2=8x的焦点是双曲线的右焦点, ∴双曲线的右焦点为(2,0),可得c==2,解得a2=1, 因此双曲线的方程为,可得a=1且b=, ∴双曲线的渐近线方程为y=x,即. 故答案为: 根据抛物线的方程,算出它的焦点为F(2,0),即为双曲线的右焦点,由此建立关于a的等式并解出a值,进而可得此双曲线的渐近线方程. 本题给出双曲线的右焦点与已知抛物线的焦点相同,求双曲线的渐近线方程.着重考查了抛物线的简单性质、双曲线的标准方程与简单几何性质等知识,属于基础题.
7.【答案】① 【解析】
解:由l,m是两条不同的直线,α,β,γ是三个不同的平面,知: 在①中,由线面垂直的性质定理得:l⊥α,m?α?l⊥m,故①正确; 在②中,l∥α,m?α?l∥m或l,m异面,故②错误; 在③中,α⊥β,α⊥γ?β与γ相交或平行,故③错误; 在④中,α⊥β,l⊥β?l∥α或l?α,故④错误. 故答案为:①. 在①中,由线面垂直的性质定理得l⊥m;在②中,l∥m或l,m异面;在③中,β与γ相交或平行;在④中,l∥α或l?α. 本题考查命题真假的判断,考查空间中线线、线面、面面间的位置关系等基础知识,考查运算求解能力,是中档题.
8.【答案】8倍 【解析】
解:设地球的半径为R,火星的半径为r,由已知条件得4πR2=4×4πr2,所以,R=2r, 所以,地球的体积为, 因此,地球体积是火星体积的8倍, 故答案为:8倍. 先利用已知条件得出地球半径与火星半径的倍数关系,再利用球体体积公式得出地球体积与火星体积的倍数关系. 本题考查球体的表面积与体积,确定地球与火星半径之间的倍数关系,是解本题的关键,属于基础题.
9.【答案】
3
2
【解析】
解:设点M(,y),∵|MO|=, ∴+(y-0)2=3, ∴y2=2或y2=-6(舍去), ∴x==1. ∴M到抛物线y2=2x的准线x=-的距离d=1-(-)=. ∵点M到该抛物线焦点的距离等于点M到抛物线y2=2x的准线的距离, ∴点M到该抛物线焦点的距离为. 故答案为:. 求得点M的坐标,将点M到该抛物线焦点的距离转化为点M到抛物线y2=2x的准线的距离即可. 本题考查抛物线的简单性质,考查转化思想与方程思想,求得点M的坐标是关键,属于中档题.
10.【答案】
2
【解析】
解:双曲线C1:=1(a>0,b>0)的左右焦点分别为F1,F2, 过F1作一条直线l交双曲线右支于点P,PF2⊥x轴,且sin∠PF1F2=,可得tan∠PF1F2=, 可得:, 可得:2c2-2a2=ac, 2e2-e-2=0.e>1; 解得e=, 故答案为:. 利用已知条件,列出方程,转化求解双曲线的离心率即可. 本题考查双曲线的简单性质的应用,考查计算能力.
11.【答案】
??
2
4
+
??
2
2
=1 【解析】
解:椭圆=1(a>b>0)的上顶点为B,左焦点为F,直线BF与直线x+y-3=0垂直, 可得kBF=1,F(-b,0),B(0,b),直线BF与直线x+y-3=0垂直,垂足为M,且点B为线段MF的中点, 可得M(b,2b),代入直线x+y-3=0,可得b=,c=,则a=2. 所求椭圆方程为:. 故答案为:. 利用直线BF与直线x+y-3=0垂直,得到直线BF的斜率,求出M的坐标,代入准线方程,即可得到b,c,然后求解a,得到椭圆方程. 本题考查椭圆的简单性质的应用,直线与椭圆的位置关系,考查转化思想以及计算能力.
12.【答案】2 【解析】
解:设圆锥N的底面直径为2r,则高为r, ∵圆柱M的底面半径为2,高为,圆柱M和圆锥N的体积相同, ∴=, 解得r=2, ∴圆锥N的底面半径为2. 故答案为:2. 设圆锥N的底面直径为2r,则高为r,利用圆柱M的底面半径为2,高为,圆柱M和圆锥N的体积相同,建立方程能求出结果. 本题考查圆柱、圆锥的体积公式,考查学生的计算能力,是中档题.
13.【答案】①③④ 【解析】
解:①∵在正方体中,D1A∥BC1,D1C∥BA1,且D1A∩DC1=D1, ∴平面D1AC∥平面A1BC1; ∵P在面对角线AC上运动, ∴D1P∥平面A1BC1;∴①正确. ②当P位于AC的中点时,D1P⊥BD不成立,∴②错误; ③∵A1C1⊥平面BDD1B1;∴A1C1⊥B1D, 同理A1B⊥B1D, ∴B1D⊥平面A1BC1, ∴平面BDD1B⊥面ACD1, ∴平面PDB1⊥平面A1BC1; ∴③正确. ④三棱锥A1-BPC1的体积等于三棱锥B-A1PC1的体积. △A1PC1的面积为定值, B到平面A1PC1的高为BP为定值, ∴三棱锥A1-BPC1的体积不变,∴④正确. 故答案为:①③④. ①根据线面平行的判断定理进行判断D1P∥平面A1BC1;? ②D利用特殊值法即可判断D1P⊥BD不成立; ③根据面面垂直的判断条件即可判断平面PDB1⊥平面A1BC1; ④将三棱锥的体积进行等价转化,即可判断三棱锥A1-BPC1的体积不变. 本题主要考查空间直线和平面平行和垂直的位置关系的判断,综合考查学生的推理能力,综合性较强,难度较大.
14.【答案】
5
2
【解析】
解:如图,由椭圆,得F(1,0), 则, . 由=,得|QF|=2|PF|,即yQ=-2yP(yP>0). 设直线l:x=my+1. 联立,可得(3m2+4)y2+6my-9=0. ∴,. 又yQ=-2yP(yP>0),解得,m=. ∴直线方程为,则直线的斜率为. 故答案为:. 由题意画出图形,写出S1,S2,结合=,可得P,Q的纵坐标的关系,设直线l:x=my+1,与椭圆方程联立,化为关于y的一元二次方程,结合根与系数的关系求m,则斜率可求. 本题考查椭圆的简单性质,考查直线与椭圆位置关系的应用,考查计算能力,是中档题.
15.【答案】证明:(1)∵D,E分别为棱AB,BC的中点, ∴DE∥AC, 又∵直三棱柱ABC-A1B1C1中,AC∥A1C1, ∴DE∥A1C1, ∵A1C1?平面A1C1F,DE?平面A1C1F, ∴DE∥平面A1C1F; (2)∵直三棱柱ABC-A1B1C1中,A1C1⊥CC1, 又∵A1C1⊥B1C1.B1C1∩CC1=C1, ∴A1C1⊥平面BCB1C1, ∵B1E?平面BCB1C1, ∴A1C1⊥B1E, ∵B1E⊥C1F,A1C1∩C1F=C1, ∴B1E⊥平面A1C1F. 【解析】
(1)由已知利用三角形的中位线的性质可求DE∥AC,由直三棱柱的性质可得AC∥A1C1,进而可证DE∥A1C1,利用线面平行的判定定理即可证明DE∥平面A1C1F; (2)先证明线面垂直A1C1⊥平面BCB1C1,利用线面垂直的性质再证明A1C1⊥B1E,利用线面垂直的判定定理即可证明B1E⊥平面A1C1F. 本题主要考查了线面平行的判定定理,线面垂直的判定定理及性质定理的应用,考查了空间想象能力和推理论证能力,属于中档题.
16.【答案】(1)证明:∵PA⊥底面ABCD,CD?底面ABCD,∴CD⊥PA. 又∵四边形ABCD为正方形,∴CD⊥AD. 又∵PA∩AD=A,∴CD⊥平面PAD. 又∵AF?平面PAD,∴CD⊥AF. ∵F为PD的中点,且PA=AD,∴PD⊥AF, 又∵PD∩CD=D,∴AF⊥平面PCD.∴PC⊥AF. (2)证明:∵平面PBC∥平面EFH,面APB∩平面PBC=PB,面PBA∩平面EFH=EH, ∴EH∥PB. 又E是线段PA的中点,H在线段AB上, ∴H是AB的中点. (3)过D作DM⊥AC于M, ∵侧棱PA⊥底面ABCD,∴PA⊥DM,且PA∩AC=A, ∴DM⊥面PAC, ∴线段DM的长就是点D到平面PAC的距离. 在直角三角形ACD中,AC?DM=DA?DC. ∴DM=
4
5
5
. ∴点D到平面PAC的距离为
4
5
5
. 【解析】
(1)要证AF⊥平面PCD即可,须证AF垂直面内两条相交直线即可; (2)由面PBC∥平面EFH,可得EH∥PB.即可证明; (3)过D作DM⊥AC于M,可得线段DM的长就是点D到平面PAC的距离. 本题考查直线与平面平行、直线与平面垂直的判定,考查空间想象能力与思维能力,考查点面距离的求法,是中档题.
17.【答案】解:(1)由已知可得,P(1,
1
2
), 当切线斜率不存在时,切线方程为x=1; 当切线斜率存在时,设切线方程为y-
1
2
=k(x-1),化为2kx-2y-2k+1=0. 由圆心(0,2)到切线的距离等于半径,得
|?4?2??+1|
4
??
2
+4
=1,解得k=-
5
12
. ∴切线方程为?
5
6
???2??+
5
6
+1=0,即5x+12y-11=0. 则切线PA,PB的方程分别为x=1,5x+12y-11=0或5x+12y-11=0,x=1; (2)设P(2a,a),则|MP|=
4
??
2
+(???2
)
2
, ∵圆M上存在点Q到点P的距离为1, ∴
4
??
2
+(???2
)
2
?1≤1,解得0≤??≤
4
5
. ∴实数a的取值范围是[0,
4
5
]. 【解析】
(1)求出P点坐标,分切线斜率存在与不存在求解; (2)设P(2a,a),则|MP|=,由圆M上存在点Q到点P的距离为1,可得,由此求得a的取值范围. 本题考查直线与圆的位置关系,考查点到直线距离公式的应用,考查数学转化思想方法,是中档题.
18.【答案】解:(1)根据题意画出图形,如图所示, 则圆的方程为x2+y2=1802, 设过点B(200,0)的直线方程为y=k(x-200),k<0; 即kx-y-200k=0, 则圆心O(0,0)到直线l的距离为d=
|?200??|
??
2
+1
=180, 化简得19k2=81, 解得k=±
9
19
; ∴tan(90°+α)=-
9
19
, ∴-
1
????????
=-
9
19
, ∴tanα=
19
9
, ∴若轮船不被风暴影响,则角α的正切值的最大值为
19
9
; (2)若轮船航行方向为北偏西45°,则直线方程为x+y=200, 则圆心O到该直线的距离为d=
|200|
2
=100
2
, 弦长为2
??
2
?
??
2
=2
180
2
?(100
2
)
2
=40
31
, 则轮船被风暴影响持续的时间为
40
31
40
=
31
. 【解析】
(1)根据题意画出图形,结合图形建立平面直角坐标系, 利用直线与圆的方程求出直线与圆相切时的斜率,即可求出角α的正切值的最大值; (2)求出直线被圆所截的弦长,再计算轮船被风暴影响持续的时间. 本题考查了直线与圆的方程应用问题,是中档题.
19.【答案】解:(1)由题意可得:2c=2
3
,
??
2
??
=
4
3
3
,a2=b2+c2, 解得:c=
3
,a=2,b=1. ∴椭圆E的标准方程为:
??
2
4
+
??
2
=1. (2)kAB=?
1
2
, ∵点P,Q关于坐标原点对称,且PQ⊥AB, ∴kPQ=2.可得直线PQ的方程为:y=2x. 联立
??
2
+4
??
2
=4
??=2??
,解得x2=
4
17
,y2=
8
17
. ∴|PQ|=2
??
??
2
+
??
??
2
=2
4
17
+
8
17
=
4
51
17
. ∴四边形ABCD的面积=
1
2
|????|?|????|=
1
2
×
5
×
4
51
17
=
2
255
17
. (3)证明:设P(x1,y1),Q(x2,y2). 设直线AP的斜率为k,(k<0),则直线方程为:y=k(x-2), 联立
??
2
+4
??
2
=4
??=??(???2)
,化为:(1+4k2)x2-16k2x+16k2-4=0, ∴2x1=
16
??
2
?4
1+4
??
2
,解得x1=
8
??
2
?2
1+4
??
2
,y1=
?4??
1+4
??
2
. ∵AP,BQ的斜率互为相反数,∴直线BQ的斜率为-k,直线方程为:y=-kx+1. 联立
??
2
+4
??
2
=4
??=?????+1
,化为:(1+4k2)x2-8kx=0, ∴x2=
8??
1+4
??
2
,y2=
1?4
??
2
1+4
??
2
. ∴PQ斜率=
1?4
??
2
1+4
??
2
?
?4??
1+4
??
2
8??
1+4
??
2
?
8
??
2
?2
1+4
??
2
=
1
2
为定值. 【解析】
(1)由题意可得:2c=2,=,a2=b2+c2,联立解出即可得出. (2)kAB=,根据点P,Q关于坐标原点对称,且PQ⊥AB,可得kPQ=2.可得直线PQ的方程为:y=2x.与题意方程联立解出可得|PQ|.可得四边形ABCD的面积. (3)设P(x1,y1),Q(x2,y2).设直线AP的斜率为k,(k<0),则直线方程为:y=k(x-2),与椭圆方程联立可得P点坐标.根据AP,BQ的斜率互为相反数,可得直线BQ的斜率为-k,直线方程为:y=-kx+1.与椭圆方程联立可得Q点坐标.再利用斜率计算公式即可得出. 本题考查了椭圆的标准方程及其性质、相互垂直的直线斜率之间的关系、四边形面积计算公式、一元二次方程的解法,考查了推理能力与计算能力,属于难题.
20.【答案】(1)解:由题意可设直线AB的方程为:y=k(x-2),A(x1,y1),B(x2,y2).则直线CD的方程为:y=-
1
??
(x-2),C,D. 联立
??
2
+3
??
2
=6
??=??(???2)
,化为:(1+3k2)x2-12k2x+12k2-6=0, ∴x1+x2=
12
??
2
1+3
??
2
,x1x2=
12
??
2
?6
1+3
??
2
, 则|AB|=
(1+
??
2
)[(
??
1
+
??
2
)
2
?4
??
1
??
2
]
=
(1+
??
2
)[
144
??
4
(1+3
??
2
)
2
?
4(12
??
2
?6)
1+3
??
2
]
=
2
6
(1+
??
2
)
1+3
??
2
. 同理可得:|CD|=
2
6
(1+
1
??
2
)
1+3×
1
??
2
=
2
6
(1+
??
2
)
3+
??
2
. ∵|AB|=
5
7
|CD|,∴
2
6
(1+
??
2
)
1+3
??
2
=
5
7
×
2
6
(1+
??
2
)
3+
??
2
. 化为:k2=2,解得k=±
2
. ∴直线AB的方程为:y=±
2
(x-2). (2)证明:设直线AB的方程为:y=k(x-2),则直线CD的方程为:y=-
1
??
(x-2),C(x3,y3),D(x4,y4). 联立
??=3
??=??(???2)
,解得M(3,k). 可得直线OM的方程:y=
??
3
x, 联立
??=
??
3
??
??=?
1
??
(???2)
,解得P(
6
3+
??
2
,
2??
3+
??
2
). 联立
??=?
1
??
(???2)
??
2
+3
??
2
=6
,化为:(3+k2)x2-12x+12-6k2=0, ∴x3+x4=
12
3+
??
2
,可得线段CD的中点坐标(
6
3+
??
2
,
2??
3+
??
2
),与点P重合. 又点O是CQ的中点,∴OP∥DQ,即OM∥DQ. 【解析】
(1)由题意可设直线AB的方程为:y=k(x-2),A(x1,y1),B(x2,y2).则直线CD的方程为:y=-(x-2),C,D.分别与椭圆方程联立,利用根与系数的关系、弦长公式即可得出|AB|=,同理可得:|CD|.根据|AB|=|CD|,解得k.即可得出直线AB的方程. (2)设直线AB的方程为:y=k(x-2),则直线CD的方程为:y=-(x-2),C(x3,y3),D(x4,y4).联立,解得M.可得直线OM的方程:y=x,联立,解得P.联立,利用根与系数的关系、中点坐标公式可得线段CD的中点坐标,得到与点P重合.又点O是CQ的中点,即可证明结论. 本题考查了椭圆的标准方程及其性质、相互垂直的直线斜率之间的关系、线段中点坐标公式、一元二次方程的根与系数的关系,考查了推理能力与计算能力,属于难题.
同课章节目录
