2018-2019学年江苏省连云港市开发区、赣榆区高二(上)期中数学试卷(解析版)
文档属性
| 名称 | 2018-2019学年江苏省连云港市开发区、赣榆区高二(上)期中数学试卷(解析版) |  | |
| 格式 | zip | ||
| 文件大小 | 136.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-01-17 20:03:28 | ||
图片预览




文档简介
2018-2019学年江苏省连云港市开发区、赣榆区高二(上)期中数学试卷
一、填空题(本大题共14小题,共70.0分)
命题“?x∈R,x2<1”的否定是______.
不等式x2-2x-3<0的解集为______.
抛物线y2=-8x的准线方程是______.
命题“若x<0,则x2≥0”的逆否命题是______.
双曲线
??
2
?
??
2
3
=1的两条渐近线所成的锐角为______.
函数f(x)=2x2+
8
??
2
+1
的最小值为______.
已知变量x,y满足约束条件
2?????+4≥0
2??+???4≤0
??+1≥0
,则z=2x+3y的最大值为______.
已知双曲线x2-
??
2
8
=
1
??
的一个焦点为(0,-3),则k的值为______.
已知椭圆
??
2
45
+
??
2
20
=1上一点P与两个焦点的连线互相垂直,若点P在第二象限,则该点的坐标为______.
过定点A(4,2)任作互相垂直的两条直线l1与l2,设11与x轴交于点M,l2与y轴交于点N,则线段MN的中点P的轨迹方程是______.
在平面直角坐标系xOy中,抛物线y2=4x的焦点为F,点M是抛物线上的动点,则
????
????
的最大值为______.
若集合A={x|4≤
2
?
??
2
+2??+??
≤9}中恰有唯一的元素,则实数a的值为______.
如图所示,点A,F分别是椭圆
??
2
??
2
+
??
2
??
2
=1(a>b>0)的下顶点和右焦点交于另一点B,过中心O作直线AF的平行线交椭圆于点C,若
????
????
=
7
20
,则椭圆的离心率为______.
已知正数x,y满足2x+
1
??
+y+
2
??
=9,则2x+y的取值范围为______.
二、解答题(本大题共6小题,共80.0分)
已知m∈R,命题p:方程
??
2
???1
+
??
2
2???
=1表示焦点在y轴上的椭圆;命题q:方程
??
2
4???
?
??
2
??+2
=1表示双曲线. (1)若命题p是真命题,求实数m的取值范围; (2)若命题“p或q”为真命题,“p且q”为假命题,求实数m的取值范围.
已知关于x的不等式ax2-4ax+1<0的解集为集合A,其中a∈R. (1)若A={x|x<-2,或x>b},求a,b的值; (2)若A=?,求实数a的取值范围.
已知不等式4x2+8x-5≤0的解集为集合A,x2-4x-m2+4≤0的解集为集合B. (1)求集合A和B; (2)当m∈(0,+∞)时,若“x∈B”是“x∈A”的必要条件,求实数m的取值范围.
已知椭圆C:ax2+by2=1. (1)若a=
1
4
,椭圆C的一条准线方程为x=4,求b的值 (2)若椭圆C与直线l:x+y=1交于点A,B,M为线段AB的中点,直线OM(O为原点)的斜率为
2
2
,又OA⊥OB,求a,b的值.
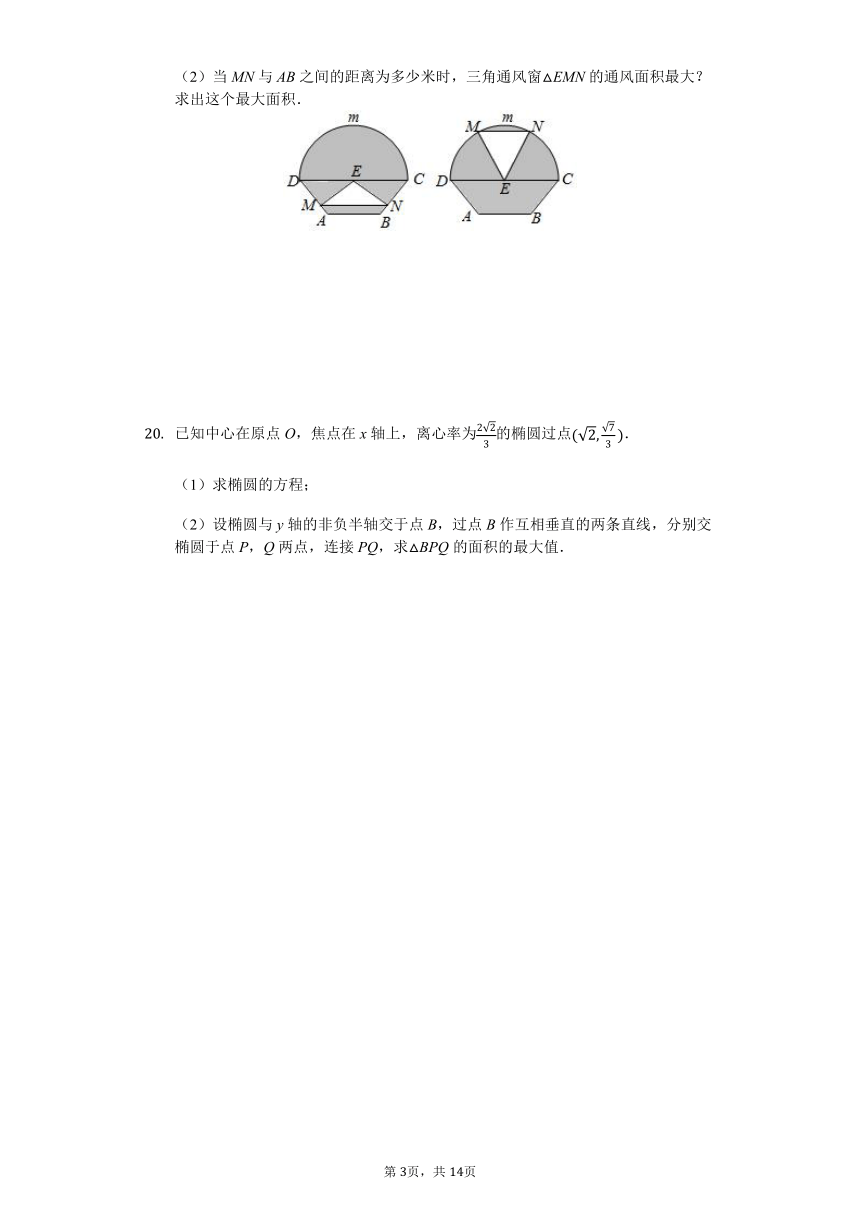
如图所示的是自动通风设施.该设施的下部ABCD是等腰梯形,其中AB=1米,高0.5米,CD=2米.上部CmD是个半圆,固定点E为CD的中点.△EMN是由电脑控制其形状变化的三角通风窗(阴影部分均不通风),MN是可以沿设施边框上下滑动且始终保持和CD平行的伸缩横杆. (1)设MN与AB之间的距离为x米,试将三角通风窗△EMN的通风面积S(平方米)表示成关于x的函数S=f(x); (2)当MN与AB之间的距离为多少米时,三角通风窗△EMN的通风面积最大?求出这个最大面积.
已知中心在原点O,焦点在x轴上,离心率为
2
2
3
的椭圆过点(
2
,
7
3
).
(1)求椭圆的方程;
(2)设椭圆与y轴的非负半轴交于点B,过点B作互相垂直的两条直线,分别交椭圆于点P,Q两点,连接PQ,求△BPQ的面积的最大值.
答案和解析
1.【答案】?x∈R,x2≥1 【解析】
解:因为命题p是全称命题,所以利用全称命题的否定是特称命题可得: ¬p:?x∈R,x2≥1 故答案为::?x∈R,x2≥1. 利用全称命题的否定是特称命题,可以求出¬p. 本题主要考查了含有量词的命题的否定,要求掌握含有量词的命题的否定的两种形式,全称命题的否定是特称命题,特称命题的否定是全称命题.
2.【答案】{x|-1<x<3} 【解析】
解:∵方程x2-2x-3=0的实数根是x1=-1,x2=3; ∴不等式x2-2x-3<0的解集为{x|-1<x<3}, 故答案为:{x|-1<x<3}, 先求对应方程x2-2x-3=0的实数根,再写出不等式的解集 本题考查了求一元二次不等式的解集问题,解题时按照解一元二次不等式的基本步骤进行解答即可.
3.【答案】x=2 【解析】
解:∵抛物线的方程为y2=-8x, ∴2p=8,p=4, ∴其准线方程为x==2. 故答案为:x=2. 利用抛物线的性质即可求得答案. 本题考查抛物线的性质,属于简单题.
4.【答案】若x2<0,则x≥0 【解析】
解:命题“若x<0,则x2≥0”的逆否命题为:若x2<0,则x≥0. 故答案为:若x2<0,则x≥0. 直接利用四种命题的逆否关系,写出逆否命题即可. 本题考查四种命题的逆否关系,注意命题的否定与否定命题的区别,是基础题.
5.【答案】60° 【解析】
解:由题意,双曲线的两条渐近线方程为y=±x, ∴两条渐近线所夹的锐角等于60°. 故答案为:60°. 先由双曲线方程求出渐近线方程,再求两条渐近线所夹的锐角即可. 本题的考点是双曲线的简单性质,主要考查双曲线的渐近线方程,考查直线的倾斜角,属于基础题.
6.【答案】6 【解析】
解:f(x)=2x2+=2(x2+1+)-2≥2×2-2=6,当且仅当x2=1时取等号, 故函数f(x)=2x2+的最小值为6, 故答案为:6. 由f(x)=2x2+=2(x2+1+)-2,利用基本不等式即可求出. 本题考查基本不等式的应用,属基础题.
7.【答案】12 【解析】
解:由变量x,y满足约束条件作出其平面区域, 由解得,x=0,y=4;A(0,4),z=2x+3y经过A时,取得最大值, 故目标函数z=2x+3y的最大值为0+3×4=12; 故答案为:12. 由题意作出其平面区域,求出A的坐标;故目标函数z=2x+3y的最大值. 本题考查了简单线性规划,作图要细致认真,属于中档题.
8.【答案】-1 【解析】
解:双曲线x2-=化为, ∵双曲线的一个焦点为(0,-3), ∴2, 解得k=-1. 故答案为:-1. 双曲线8kx2-ky2=8化为标准形式,由于双曲线的一个焦点为(0,-3),列出方程,解出k即可 本题考查了双曲线的标准方程及其性质,考查运算能力,属于基础题.
9.【答案】(-3,4) 【解析】
解:∵椭圆=1,∴a2=45,b2=20, c2=a2-b2=25 以O为圆心,半径5的圆方程 x2+y2=25 (1) =1 (2) 由(1)(2)得: x2=9,y2=16 解得:x1=-3,x2=3,y1=4,y2=-4, 椭圆=1上一点P与两个焦点的连线互相垂直, 即椭圆与圆的交点, 若点P在第二象限, 所以交点坐标是(-3,4), 故答案为:(-3,4). 以椭圆的中心为圆心,以半焦距为半径的圆,椭圆与圆的交点即为所求. 本题主要考查椭圆的性质,属于基本知识的考查.
10.【答案】2x+y-5=0 【解析】
解:当l1不平行于坐标轴时,设l1:y-2=k(x-4)…① 则l2:y-2=-(x-4)…② 在①中令y=0得,M(4-,0),在②中令x=0得,N(0,2+). 设MN的中点P(x,y),则,消去k得,2x+y-5=0, 当l1平行于坐标轴时,MN的中点为(2,1)也满足此方程. ∴P点的轨迹方程为2x+y-5=0. 故答案为:2x+y-5=0. 通过当l1不平行于坐标轴时,设l1:y-2=k(x-4),l2:y-2=-(x-4),求出M,N的坐标,设MN的中点P(x,y),消去k得轨迹方程,当l1平行于坐标轴时,判断是否满足方程即可. 本题考查轨迹方程的求法,注意直线的斜率是否存在是解题的易错点,是中档题.
11.【答案】
2
3
3
【解析】
解:焦点F(1,0),设M(m,n),则n2=4m,m>0,设M?到准线x=-1的距离等于d, 则==. 令2m-1=t,t>-1,则m=(t+1), ∴=≤=(当且仅当t=3时,等号成立). 则的最大值为:. 故答案为: 设M到准线的距离等于d,由抛物线的定义可得=,令2m-1=t,利用基本不等式求得最大值. 本题考查抛物线的定义、简单性质,体现了换元的思想,基本不等式的应用是解题的关键和难点,属于中档题.
12.【答案】2 【解析】
解:∵集合A={x|4≤9}中恰有唯一的元素, ∴2≤-x2+2x+a≤log29恰有唯一解, ∵1≤a-(x-1)2≤log29-1, ∴实数a的值为2. 故答案为:2. 推导出2≤-x2+2x+a≤log29恰有唯一解,从而2≤a-(x-1)2≤log29-1,由此能求出实数a的值. 本题考查满足条件的实数值的求法,是基础题,解题时要认真审题,注意集合中元素个数、指数函数的性质的合理运用.
13.【答案】
3
4
【解析】
解:由题意,设A(0,-b),F(c,0), AB的方程为y=x-b, 则OC的方程为y=x, AB的方程与椭圆方程联立可得(a2+c2)x2-2a2cx=0, ∴x=0或x=, 可得B(,), ∴|FB|==, OC的方程与椭圆方程联立可得(a2+c2)x2=a2c2, ∴x=±,即有C(,), ∴|OC|==, ∵==, 化为400c4-849c2a2+351a4=0, 由e=可得400e4-849e2+351=0, 即有e2=或>1(舍去), 则e=. 故答案为:. 设出AB,CO的方程,分别与椭圆方程联立,求导|CO|,|FB|,利用=,即可求得椭圆的离心率. 本题考查椭圆的离心率,考查直线与椭圆的位置关系,解题的关键是求出|CO|,|FB|,属于中档题.
14.【答案】[1,8] 【解析】
解:2x++y+=9, ∴9-(2x+y)=+==≥=,当且仅当2x=y取等号, 设2x+y=t,t>0, ∴9-t≥, 即t2-9t+8≤0, 解得1≤t≤8, 故2x+y的取值范围为[1,8], 故答案为:[1,8] 由题意和基本不等式整体可得9-(2x+y)≥的不等式,解不等式可得. 本题考查基本不等式,涉及换元法和不等式的解法,属基础题.
15.【答案】解:(1)若命题p是真命题,则2-m>m-1>0,解得1<m<
3
2
; (2)若命题q为真命题,则(4-m)(m+2)>0,即-2<m<4. 命题“p或q”为真命题,“p且q”为假命题,则p,q一真一假. 当p真q假时,
1<??<
3
2
??≤?2或??≥4
,得m∈?; 当p假q真时,
??≤1或??≥
3
2
?2<??<4
,解得-2<m≤1或
3
2
≤??<4. ∴实数m的取值范围时(-2,1]∪[
3
2
,4). 【解析】
(1)由题意可得,2-m>m-1>0,求解不等式得答案; (2)求出q为真命题的m的范围,再由复合命题的真假判断列式求解. 本题考查复合命题的真假判断,考查椭圆与双曲线的性质,是中档题.
16.【答案】解:(1)A={x|x<-2,或x>b}时,不等式ax2-4ax+1<0对应方程的解为-2和b, 且a<0,∴4a+8a+1=0,解a=-
1
12
,∴不等式x2-4x-12>0,解得x<-2或x>6, ∴b=6; (2)若A=?,则
△≤0
??>0
, 即
16
??
2
?4??≤0
??>0
, 解得
??>0
0≤??≤
1
4
, 即实数a的取值范围是0<a≤
1
4
. 【解析】
(1)根据一元二次不等式与对应方程的关系,即可求出a和b的值; (2)由题意,利用判别式即可求得a的取值范围. 本题考查了一元二次不等式与对应方程的应用问题,是基础题.
17.【答案】解:(1)∵4x2+8x-5≤0的解集为集合A, ∴A=[-
5
2
,
1
2
]; ∵x2-4x-m2+4≤0的解集为集合B, ∴B=[2-|m|,2+|m|]; (2)当m∈(0,+∞)时: B=[2-m,2+m], 若“x∈B”是“x∈A”的必要条件, 则A?B, 则
2???≤?
5
2
2+??≥
1
2
,解得:m≥
9
2
. 【解析】
(1)解不等式求出A,B即可; (2)根据集合的包含关系得到关于m的不等式组,解出即可. 本题考查了不等式的解法,考查集合的包含关系,是一道常规题.
18.【答案】解(1)a=
1
4
时,椭圆方程化为:
??
2
1
??
+
??
2
1
??
=1, ∴
1
??
1
??
?
1
??
=4,即
4
4?
1
??
=4,解得:b=
1
3
, (2)设A(x1,y1),B(x2,y2),联立
??
??
2
+??
??
2
=1
??+??=1
,消去y并整理得:(a+b)x2-2bx+b-1=0, ∴△=(-2b)2-4(a+b)(b-1)>0,得a+b>ab, x∴1+x2=
2??
??+??
,x1x2=
???1
??+??
, ∴y1+y2=2-(x1+x2)=
2??
??+??
,y1y2=1-(x1+x2)+x1x2=
???1
??+??
, ∴kOM=
??
1
+
??
2
2
??
1
+
??
2
2
=
??
??
=
2
2
,OA⊥OB?1x2+y1y2=0?
???1
??+??
+
???1
??+??
=0?a+b=2,
??
??
=
2
2
??+??=2
解得:a=2
2
-2??????????b=4-2
2
【解析】
(1)根据椭圆的几何性质列式:=4,即=4,解得:b=; (2)联立直线与椭圆,用根与系数关系、斜率公式以及OA⊥OB?1x2+y1y2=0列式解得a与b. 本题考查了直线与椭圆的综合.属中档题.
19.【答案】解:(1)①当0≤x<0.5时,△EMN的高是0.5-x,底是1+2x(可以由三角形相似得到), ∴f(x)=
1
2
(0.5-x)(1+2x)=
1
2
(0.5-2x2), ②当1.5≥x≥0.5时,△EMN的高是x-0.5,底是2
1?(0.5???
)
2
, ∴f(x)=(x-0.5)
3+4???4
??
2
4
, ∴f(x)=
1
2
(
1
2
?2
??
2
)
0≤??<
1
2
(???
1
2
)
3+4???4
??
2
4
1
2
≤??≤
3
2
, (2)当0≤x<0.5时,f(x)是单调递减的,f(x)的最大值为f(0)=
1
4
, 当1.5≥x≥0.5时,f(x)是在(
1
2
,
1+
2
2
)上单调递增,在(
1+
2
2
,
3
2
)上单调递减, ∴f(x)的最大值为f(
1+
2
2
)=
1
2
, ∴当x=
1+
2
2
时,三角形面积最大,最大面积为
1
2
. 【解析】
(1)三角形的面积与x的关系是分段函数,所以分类讨论即可. (2)求出每一段上的最大值.再找到最大的一个即可. 本题考查分段函数求解析式,所以分类讨论即可.求最大值时,只需求出每一段上的最大值,再找到最大的一个即可.
20.【答案】解:(Ⅰ)由题意可设椭圆方程为
??
2
??
2
+
??
2
??
2
=1(??>??>0),则
??
??
=
2
2
3
2
??
2
+
7
9
??
2
=1
,故
??=1
??=3
, 所以,椭圆方程为
??
2
9
+
??
2
=1. (Ⅱ)由题意可知,直线BP的斜率存在且不为o. 故可设直线BP的方程为y=kx+1,由对称性,不妨设k>0, 由
??
2
+9
??
2
?9=0
??=????+1
,消去y得(1+9k2)x2+18kx=0, 则|????|=
1+
??
2
18??
1+9
??
2
,将式子中的k>0换成?
1
??
, 得:|????|=
18
1+
??
2
??
2
+9
.
??
△??????
=
1
2
|????||????| =
1
2
?
18??
??
2
+1
1+9
??
2
?
18
??
2
+1
??
2
+9
=
1
2
??
2
+1
18??
1+9
??
2
1
??
2
+1
18
1
??
1+
9
??
2
=
??
2
+1
1
??
2
+1
162
(1+9
??
2
)(1+
9
??
2
)
=(??+
1
??
)
162
82+9(
??
2
+
1
??
2
)
, 设??+
1
??
=??,则t≥2. 故
??
△??????
=
162??
9
??
2
+64
=
162
9??+
64
??
≤
162
2
9×64
=
27
8
,取等条件为9??=
64
??
即??=
8
3
, 即??+
1
??
=
8
3
,解得??=
4±
7
3
时,S△BPQ取得最大值
27
8
. 【解析】
(Ⅰ)设出椭圆的方程;利用椭圆的离心率,经过的点,求出a,b即可得到椭圆方程. (Ⅱ)直线BP的斜率存在且不为0.设直线BP的方程为y=kx+1,联立直线与椭圆方程,通过韦达定理以及弦长公式,表示三角形的面积,利用基本不等式转化求解最值即可. 本题考查直线与椭圆的位置关系的综合应用,椭圆方程的求法,基本不等式的应用,考查转化思想以及计算能力.
同课章节目录
