2018-2019学年江苏省南京市鼓楼区高二(上)期中数学试卷(文科)(解析版)
文档属性
| 名称 | 2018-2019学年江苏省南京市鼓楼区高二(上)期中数学试卷(文科)(解析版) |  | |
| 格式 | zip | ||
| 文件大小 | 118.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-01-17 20:14:08 | ||
图片预览




文档简介
2018-2019学年江苏省南京市鼓楼区高二(上)期中数学试卷(文科)
一、填空题(本大题共14小题,共70.0分)
命题“?x∈R,x2>9”的否定是______.
“x>1”是“x2>1”的______条件(填“充分不必要”、“必要不充分”、“充要”、“既不充分也不必要”)
函数f(x)=x2在区间[1,1.1]上的平均变化率是______.
已知函数f(x)=2ex-x的导数为f′(x),则f′(0)的值是______.
已知直线l1:ax+4y+4=0,l2:x+ay+2=0,若l1∥l2,则a的值是______.
已知点A(1,2),B(3,4),若直线x+ky+5=0与线段AB有公共点,则实数k的取值范围是______.
(理科)若x,y满足约束条件
??≥0
??+2??≥3
2??+??≤3
,则z=x-y的最小值是______.
已知双曲线x2-y2=k的一个焦点是抛物线y2=16x的焦点,则k的值是______.
若圆x2+y2=4与圆x2+y2-16x+m=0相外切,则实数m的值是______.
若经过椭圆
??
2
??
2
+
??
2
??
2
=1(a>b>0)的焦点且垂直于x轴的直线被椭圆截得的线段长为
??
2
,则该椭圆的离心率为______.
已知椭圆
??
2
??
2
+
??
2
??
2
?4
=1的左、右焦点分别为F1、F2,若在椭圆上存在点P使得PF1⊥PF2,且△PF1F2的面积是2,则a2的值是______.
已知圆(x-3)2+(y-4)2=4的圆心为C,点P,Q在圆上,若△CPQ的面积是
3
,则C到直线PQ的距离为______.
在平面直角坐标系xOy中,已知点A(1,0),B(4,0),若直线x-y+m=0上存在唯一的点P使得PB=2PA,则m的值是______.
在平面直角坐标系xOy中,已知双曲线
??
2
??
??
2
??
-t2y2=1(t∈[2,3])的右焦点为F,过F作双曲线的渐近线的垂线,垂足为H,则△OFH面积的取值范围为______.
二、解答题(本大题共6小题,共80.0分)
已知p:方程
??
2
???1
+
??
2
???4
=1表示双曲线,q:
??
2
??+2
+
??
2
6???
=1表示焦点在x轴上的椭圆. (1)若“p且q”是真命题,求实数m的取值范围; (2)若“p且q”是假命题,“p或q”是真命题,求实数m的取值范围.
在平面直角坐标系xOy中,已知直线y=-2x+1与圆O:x2+y2=r2(r>0)交于M,N两点,且MN=
4
5
5
. (1)求M,N的坐标; (2)求过O,M,N三点的圆的方程.
已知点A(
1
2
,-1),B(2,1),函数f(x)=log2x. (1)过原点O作曲线y=f(x)的切线,求切线的方程; (2)曲线y=f(x)(
1
2
≤x≤2)上是否存在点P,使得过P的切线与直线AB平行?若存在,则求出点P的横坐标,若不存在,则请说明理由.
在平面直角坐标系xOy中,已知点A(0,a)(a是正常数),抛物线y=px2的焦点是(0,1),P是抛物线上的动点. (1)求抛物线的方程; (2)若PA的最小值是2
3
,求a的值.
设f(x)=(1-m)lnx+
??
2
??
2
+nx(m,n是常数). (1)若m=0,且f(x)在(1,2)上单调递减,求n的取值范围; (2)若m>0,且n=-1,求f(x)的单调区间.
在平面直角坐标系xOy中,已知椭圆
??
2
??
2
+
??
2
??
2
=1(a>b>0)离心率是
1
2
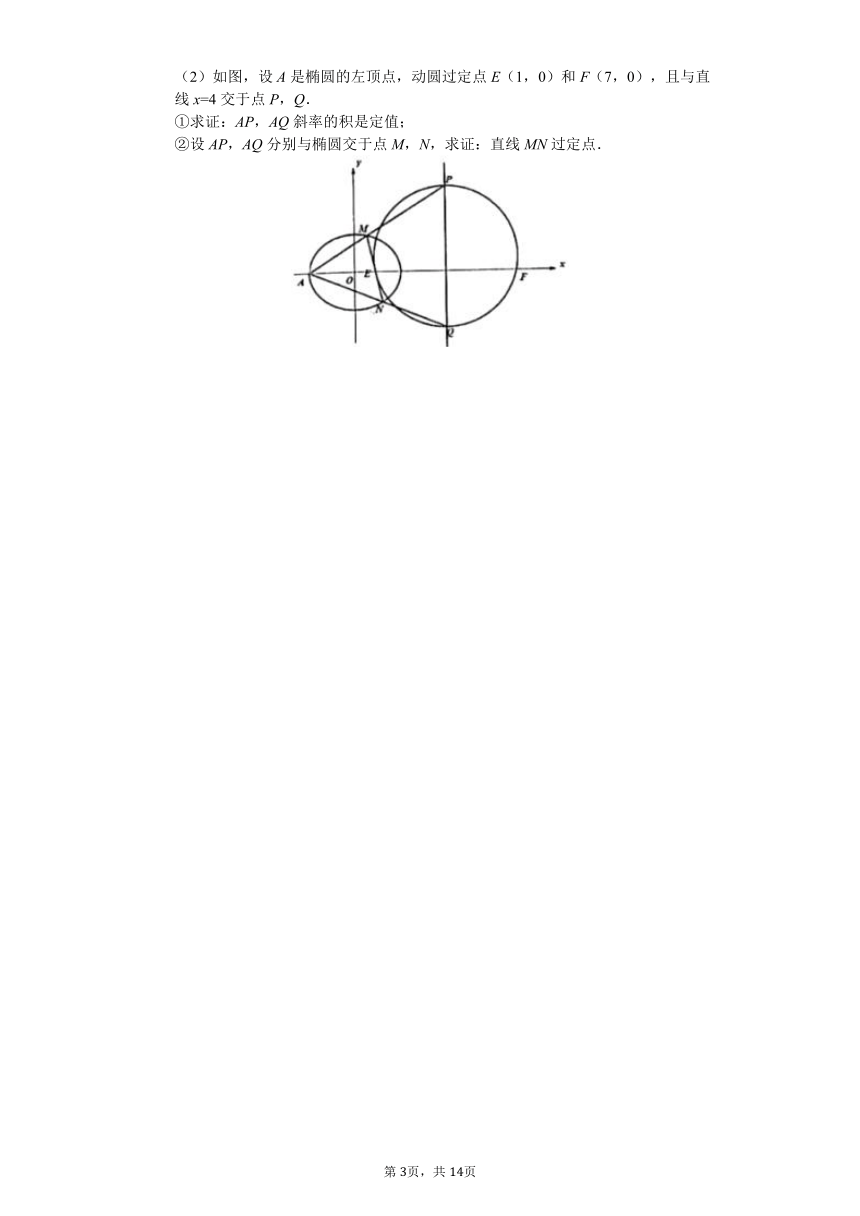
,焦点到相应准线的距离是3. (1)求椭圆的方程; (2)如图,设A是椭圆的左顶点,动圆过定点E(1,0)和F(7,0),且与直线x=4交于点P,Q. ①求证:AP,AQ斜率的积是定值; ②设AP,AQ分别与椭圆交于点M,N,求证:直线MN过定点.
答案和解析
1.【答案】?x∈R,x2≤9 【解析】
解:命题“?x∈R,x2>9”的否定是命题“?x∈R,x2≤9”, 故答案为:?x∈R,x2≤9. 由已知中的原命题,结合特称命题否定的定义,可得答案. 本题考查的知识点是特称命题的否定,难度不大,属于基础题.
2.【答案】充分不必要 【解析】
解:由x2>1得x>1或x<-1. ∴“x>1”是“x2>1”的充分不必要条件. 故答案为:充分不必要. 利用充分条件和必要条件的定义进行判断. 本题主要考查充分条件和必要条件的应用,利用向量相等的定义是解决本题的关键.
3.【答案】2.1 【解析】
解:∵f(x)=x2,∴f(1)=1,f(1.1)=1.21, ∴该函数在区间[1,1.1]上的平均变化率为=2.1 故答案为:2.1 利用函数的解析式求出区间两个端点的函数值,再利用平均变化率公式求出该函数在区间[1,1.1]上的平均变化率. 本题考查函数在区间上的平均变化率,考查学生的计算能力,属于基础题.
4.【答案】1 【解析】
解:函数f(x)=2ex-x的导数为f′(x)=2ex-1,则f′(0)=2-1=1, 故答案为:1 先求导,再代值计算即可. 本题考查了基本导数公式和导数值的求法,属于基础题
5.【答案】-2 【解析】
解:∵直线l1:ax+4y+4=0,l2:x+ay+2=0,若l1∥l2,则a=0时,不满足条件,∴a≠0, 且=≠,求得a=-2, 故答案为:-2. 由题意利用两条直线平行的性质,求得a的值. 本题主要考查两条直线平行的性质,属于基础题.
6.【答案】[-3,-2] 【解析】
解:直线x+ky+5=0经过定点P(-5,0), ∴kPA==,kPB==. ∵直线x+ky+5=0与线段AB有公共点, ∴≤-≤,解得:-3≤k≤-2. 故答案为:[-3,-2]. 直线x+ky+5=0经过定点P(-5,0),可得kPA≤-≤kPB. 本题考查了直线的斜率计算公式及其应用,考查了推理能力与计算能力,属于基础题.
7.【答案】-3 【解析】
解:设变量x、y满足约束条件,在坐标系中画出可行域三角形, 将z=x-y整理得到y=x-z,要求z=x-y的最小值即是求直线y=x-z的纵截距的最大值, 当平移直线x-y=0经过点A(0,3)时,x-y最小, 且最小值为:-3, 则目标函数z=x-y的最小值为-3. 故答案为:-3. 先根据条件画出可行域,设z=x-y,再利用几何意义求最值,将最小值转化为y轴上的截距最大,只需求出直线z=x-y,过可行域内的点A(0,3)时的最小值,从而得到z最小值即可. 借助于平面区域特性,用几何方法处理代数问题,体现了数形结合思想、化归思想.线性规划中的最优解,通常是利用平移直线法确定.
8.【答案】8 【解析】
解:抛物线y2=16x的焦点坐标为(4,0) 故双曲线x2-y2=k的焦点在x轴, 即k>0, 双曲线x2-y2=k的标准方程为:, 故2k=16, 解得:k=8, 故答案为:8. 由已知可靠是双曲线x2-y2=k的焦点在x轴,且c=4,进而得到答案. 本题考查的知识点双曲线的性质,抛物线的性质,难度不大,属于基础题.
9.【答案】28 【解析】
解:x2+y2-16x+m=0的圆心为(8,0),半径r=, ∴圆心距:8=2+,解得:m=28, 故答案为:28. 两圆外切等价于圆心距等于两圆半径之和. 本题考查了圆与圆的位置关系及其判定,属基础题.
10.【答案】
3
2
【解析】
解:因为过椭圆的焦点垂直于x轴的弦长为, 所以,又b2=a2-c2, 所以3a2=4c2, 所以椭圆的离心率为:. 故答案为:. 椭圆的通经等于过椭圆的焦点垂直于x轴的弦长为,建立方程,然后求出椭圆的离心率. 本题考查椭圆的基本性质,椭圆离心率的求法,考查计算能力.
11.【答案】6 【解析】
解:根据椭圆定义知|PF1|+|PF2|=2a,由PF1⊥PF2, 得△PF1F2为直角三角形, ∴(|PF1|)2+(|PF2|)2=(2c)2, 又∵△PF1F2的面积为2, ∴?|PF1|?|PF2|=2,则|PF1|?|PF2|=4, ∴(2a)2=(|PF1|+|PF2|)2 =(|PF1|)2+(|PF2|)2+2|PF1|?|PF2|=4c2+8, 即b2=a2-c2=2,则a2-4=2, ∴a2=6, 故答案为:6. 通过椭圆定义知|PF1|+|PF2|=2a,由PF1⊥PF2,可知(|PF1|)2+(|PF2|)2=(2c)2,利用△PF1F2的面积为2可得?|PF1|?|PF2|=2,则(2a)2=(|PF1|+|PF2|)2=(|PF1|)2+(|PF2|)2+2|PF1|?|PF2|,代入计算即可. 本题考查椭圆定义、直角三角形的面积及勾股定理等基础知识,注意解题方法的积累,属于中档题.
12.【答案】1或
3
【解析】
解:根据题意,设C到直线PQ的距离为d, 圆(x-3)2+(y-4)2=4的半径r=2, 若△CPQ的面积是,则S=×d×2=, 即d×=, 解可得:d=1或; 故答案为:1或. 根据题意,设C到直线PQ的距离为d,分析圆的半径,由直线与圆相交的性质可得S=×d×2=,变形解可得d的值,即可得答案. 本题考查直线与圆的位置关系,注意利用勾股定理分析,属于基础题.
13.【答案】±2
2
【解析】
解:设P(x,y),则由PB=2PA得=2,化简得:x2+y2=4, 依题意得,直线x-y+m=0与圆x2+y2=4有唯一交点,即相切. 所以=2,解得m=±2 故答案为 先求出点P的轨迹方程为圆:x2+y2=4,然后问题转化为直线x-y+m=0与圆相切. 本题考查了两点间的距离.属中档题.
14.【答案】[
????2
4
,
1
2??
] 【解析】
解:在双曲线-t2y2=1中a2=ln2t,b2=, ∴c2=a2+b2=ln2t+,a=lnt,b= ∴右焦点为F(,0),渐近线方程为y=±x, ∴|FH|==, ∴|OH|=a=lnt, ∴△OFH面积S=f(t)=,t∈[2,3], ∴f′(t)=, 令f′(t)=0,解得t=e, 当t∈[2,e]时,f′(t)>0,函数f(t)单调递增, 当t∈(e,3]时,f′(t)<0,函数f(t)单调递减, ∴f(t)max=f(e)=, ∵f(2)=,f(3)=, ∴f(2)-f(3)=-==<0, ∴f(t)min=f(2)=, 故△OFH面积的取值范围为[,] 故答案为:[,] 根据双曲线的简单性质和渐近线方程,以及点到直线的距离公式求出|FH|═,|OH|=a=lnt,表示出三角形的面积,构造函数,利用导数求出函数的最值. 本题考查了双曲线的简单性质和导数和函数的最值的关系,考查了转化能力和运算能力,属于中档题
15.【答案】解:(1)命题p:方程
??
2
???1
+
??
2
???4
=1表示双曲线, 则(m-1)(m-4)<0,解得1<m<4; 命题q:
??
2
??+2
+
??
2
6???
=1表示焦点在x轴上的椭圆, 则m+2>6-m>0,解得2<m<6; 若“p且q”是真命题,则
21,解得2<m<6, ∴实数m的取值范围是2<m<6; (2)若“p且q”是假命题,“p或q”是真命题, 则p、q一真一假; 当p真q假时,
??≤2或??≥6
1, 解得1<m≤2; 当p假q真时,
2??≤1或??≥4
, 解得4≤m<6; 综上,实数m的取值范围是1<m≤2或4≤m<6. 【解析】
(1)求出命题p、q为真命题时m的取值范围,再根据“p且q”是真命题求出m的取值范围; (2)当“p且q”是假命题,“p或q”是真命题时,p、q一真一假,由此求出m的取值范围. 本题考查了椭圆与双曲线的定义与应用问题,也考查了复合命题的真假性问题,是中档题.
16.【答案】解:(1)根据题意,圆O:x2+y2=r2的圆心为(0,0), 圆心O到直线y=-2x+1的距离d=
|?1|
4+1
=
5
5
, 又由|MN|=
4
5
5
,则2×
??
2
?
??
2
=
??
2
?
1
5
=
4
5
5
,解可得r=1; 则圆的方程为x2+y2=1, 联立
??=?2??+1
??
2
+
??
2
=1
,解可得
??=1
??=0
或
??=
4
5
??=?
3
5
, 即M、N的坐标为(0,1)或(
4
5
,-
3
5
); (2)由(1)的结论,M、N的坐标为(0,1)或(
4
5
,-
3
5
); 设过O,M,N三点的圆的方程为x2+y2+Dx+Ey+F=0, 则有
??=0
1+??=0
(
4
5
)
2
+(?
3
5
)
2
+
4
5
×???
3
5
×??+??=0
, 解可得:F=0,E=-1,D=-2, 则要求圆的方程为x2+y2-2x-y=0. 【解析】
(1)根据题意,求出圆x2+y2=r2的圆心到直线y=-2x+1的距离d,又由|MN|=,结合直线与圆的位置关系可得2×==,解可得r的值,即可得圆O的方程,联立直线与圆的方程,解可得M、N的坐标, (2)根据题意,设过O,M,N三点的圆的方程为x2+y2+Dx+Ey+F=0,则有,解可得D、E、F的值,代入圆的方程即可得答案. 本题考查直线与圆的位置关系,涉及直线与圆相交的性质以及弦长的计算,属于综合题.
17.【答案】解:(1)设切点为(m,log2m), 函数f(x)=log2x导数为f′(x)=
1
??????2
, 由题意可得
1
??????2
=
????
??
2
??
??
, 解得m=e, 则切线方程为y=ex: (2)A(
1
2
,-1),B(2,1)的斜率为kAB=
4
3
, 设P(n,log2n), 假设存在点P,使得过P的切线与直线AB平行, 可得
1
??????2
=
4
3
,可得n=
3
4????2
,
1
2
<
3
4????2
<2, 则曲线y=f(x)(
1
2
≤x≤2)上存在点P,使得过P的切线与直线AB平行, 且P的横坐标为
3
4????2
. 【解析】
(1)设切点为(m,log2m),求得f(x)的导数,可得切线的斜率,再由两点的斜率公式,计算可得所求方程; (2)设P(n,log2n),求得导数可得切线的斜率,由两点的斜率公式,以及两直线平行的条件:斜率相等,可得P的横坐标. 本题考查导数的运用:求切线方程,考查导数的几何意义,直线的斜率和直线方程的运用,考查方程思想和运算能力,属于基础题.
18.【答案】解:(1)∵抛物线y=px2的焦点是(0,1),∴
1
4??
=1,p=
1
4
. ∴抛物线的方程为:y=
1
4
??
2
. (2)设P(x,y),y≥0.x2=4y PA2=x2+(y-a)2=[y-(a-2)]2+4a-4. PAmax=
4???4
,??≥2
??,??<2
, ∵PA的最小值是2
3
,a的值为4. 【解析】
(1)可得,p=.即可得抛物线的方程. (2)设P(x,y),y≥0.x2=4y,PA2=x2+(y-a)2=[y-(a-2)]2+4a-4. PAmax=,即可得a的值. 本题考查了抛物线的简单几何性质,考查了分段函数的运用,训练了分段函数最值得求法,是中档题.
19.【答案】解:(1)m=0时,f(x)=lnx+nx,f′(x)=
1
??
+n, ∵f(x)在(1,2)递减,故x∈(1,2)时
1
??
+n≤0成立, 故n≤-
1
??
在x∈(1,2)时成立, 故n的范围是(-∞,-1]; (2)∵m>0,n=-1, ∴f(x)=(1-m)lnx+
??
2
x2-x, f′(x)=
??
??
(x-1)(x-
1???
??
),其中x>0, ①当m≥1时,
1???
??
<0,在区间(0,1]上,f′(x)<0, 在区间[1,+∞)上,f′(x)>0, 故f(x0在(0,1)递减,在(1,+∞)递增; ②当
1
2
<m<1时,0<
1???
??
<1, 在区间(0,
1???
??
)和(1,+∞)上,f′(x)>0, 在区间(
1???
??
,1)上,f′(x)<0, 故f(x)在(0,
1???
??
),(1,+∞)递增,在(
1???
??
,1)递减, ③当m=
1
2
时,
1???
??
=1, 在区间(0,+∞)上,f′(x)≥0,(仅在x=1时,f′(x)=0), 故f(x)在(0,+∞)递增,无递减区间, ④当0<m<
1
2
时,
1???
??
>1, 在区间(0,1)和(
1???
??
,+∞)上,f′(x)>0,在区间(1,
1???
??
)上,f′(x)<0, 故f(x)在(0,1)和(
1???
??
,+∞)递增,在(1,
1???
??
)递减. 【解析】
(1)代入m的值,求出函数的导数,得到n≤-在x∈(1,2)时成立,求出n的范围即可; (2)求出函数的导数,通过讨论m的范围,求出函数的单调区间即可. 本题考查了函数的单调性问题,考查导数的应用以及分类讨论思想,转化思想,是一道综合题.
20.【答案】解:(1)设椭圆的焦距为2c(c>0),由题意可得
??
??
=
1
2
,所以,a=2c, 因为椭圆的焦点到相应准线的距离为
??
2
??
???=
(2??
)
2
??
???=3??=3,得c=1,所以,a=2c=2,??=
??
2
?
??
2
=
3
, 因此,椭圆的方程为
??
2
4
+
??
2
3
=1; (2)①设动圆的圆心坐标为(4,t),则圆的方程为(x-4)2+(y-t)2=t2+9, 设点P(xP,yP)、Q(xQ,yQ),令x=4,可得yPyQ=-9, 则AP、AQ的斜率之积为
??
??
6
×
??
??
6
=
?9
36
=?
1
4
(定值); ②设直线MN的方程为x=my+t,设点M(x1,y1)、N(x2,y2)< 将直线MN的方程代入椭圆方程并化简得(3m2+4)y2+6tmy+3t2-12=0, 由韦达定理可得
??
1
+
??
2
=?
6????
3
??
2
+4
,
??
1
??
2
=
3
??
2
?12
3
??
2
+4
, 因为A、M、P三点共线,则
????
∥
????
, 由于
????
=(
??
1
+2,
??
1
)=(??
??
1
+??+2,
??
1
),
????
=(6,
??
??
), 所以6y1=(my1+t+2)yP,则
??
??
=
6
??
1
??
??
1
+(??+2)
,同理可得
??
??
=
6
??
2
??
??
2
+(??+2)
, 由
??
??
??
??
=
36
??
1
??
2
[??
??
1
+(??+2)][??
??
2
+(??+2)]
=
36
??
1
??
2
??
2
??
1
??
2
+??(??+2)(
??
1
+
??
2
)+(??+2
)
2
=
36(3
??
2
?12)
3
??
2
+4
??
2
(3
??
2
?12)
3
??
2
+4
?
6
??
2
??(??+2)
3
??
2
+4
+(??+2
)
2
=
36(3
??
2
?12)
4(??+2
)
2
=
27(???2)
??+2
=?3,解得t=1, 因此,直线MN过定点(1,0). 【解析】
(1)由椭圆的离心率得到a=2c,结合焦点到相应准线的距离可求出c的值,进而求出a、b的值,即可得出椭圆的方程; (2)①设动圆圆心坐标为(4,t),进而写出动圆的方程,将直线x=4的方程代入圆的方程,得出点P、Q两点的纵坐标之积,再利用斜率公式可得出AP、AQ的斜率之积为定值; ②设直线MN的方程为x=my+t,将直线MN的方程与椭圆的方程联立,列出韦达定理,由P、Q两点的纵坐标之积为-9,结合韦达定理计算出t=1,从而得出直线MN过定点(1,0). 本题考查直线与椭圆的综合问题,考查计算能力与推理能力,属于难题.
同课章节目录
