2018-2019学年江苏省苏州市常熟市高二(上)期中数学试卷(解析版)
文档属性
| 名称 | 2018-2019学年江苏省苏州市常熟市高二(上)期中数学试卷(解析版) |  | |
| 格式 | zip | ||
| 文件大小 | 163.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-01-17 20:12:38 | ||
图片预览




文档简介
2018-2019学年江苏省苏州市常熟市高二(上)期中数学试卷
一、填空题(本大题共14小题,共70.0分)
过点(1,0),且斜率为2的直线方程是______.
若A(3,-2),B(-5,2),C(x,0)三点共线,则实数x的值为______.
若圆(x-a)2+(y-b)2=r2(r>0)的圆心位于第一象限,则直线y=ax+b不经过第______象限.
已知点P(2a,a)在圆(x-a)2+(y+a)2=20的内部,则实数a的取值范围是______.
若圆C的半径为2,其圆心与点(1,0)关于直线y=x对称,则圆C的标准方程为______.
若直线l1:x+(1+m)y+m-2=0与l2:2mx+4y+16=0平行,则实数m的值为______.
若将一个底面半径为1的圆锥侧面沿一条母线展开,其展开图是半圆,则该圆锥的高为______.
长方体的过一个顶点的三条棱长的比是1:2:3,对角线长为2
14
,则这个长方体的表面积是______.
若直线ax+by+7=0与圆x2+y2+4x-1=0切于点P(-3,2),则ab的值为______.
设m,n为不重合的两条直线,α,β为不重合的两个平面,则下列命题中,所有真命题的个数是______. ①若m∥α,n∥α,则m∥n;②若m⊥α,m⊥β,则α∥β; ③若m∥α,m⊥β,则α⊥β;④一定存在直线l,使得l∥α,l∥β.
直线l过点??(1,
1
2
),且截圆x2+y2=4所得的弦长为2
3
,则直线l的方程为______.
如图,在直四棱柱ABCD-A1B1C1D1 中,点E,F分别在AA1,CC1上,且AE=
3
4
AA1,CF=
1
3
CC1,点A,C到BD的距离之比为3:2,则三棱锥E-BCD和F-ABD的体积比
??
?????????
??
?????????
=______.
已知点B在圆O:x2+y2=16上,??(2,2),
????
=
????
+
????
,若存在点N使得MN为定长,则点N的坐标是______.
如图,已知平面α⊥平面β,A,B是平面α与平面β的交线上的两个定点,DA?β,CB?β,且DA⊥AB,CB⊥AB,AD=4,BC=8,AB=6,在平面α内有一个动点P,使得∠APD=∠BPC,则△PAB的面积的最大值是______.
二、解答题(本大题共6小题,共80.0分)
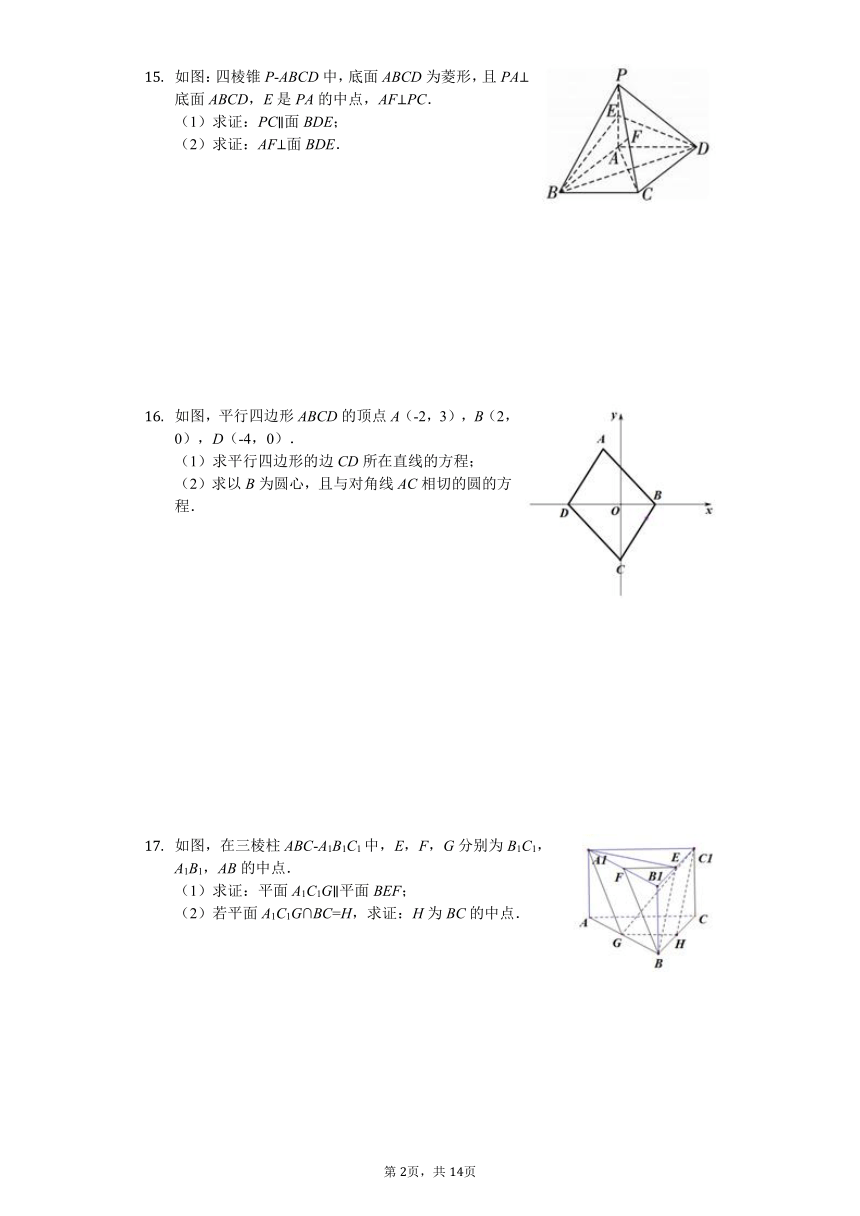
如图:四棱锥P-ABCD中,底面ABCD为菱形,且PA⊥底面ABCD,E是PA的中点,AF⊥PC. (1)求证:PC∥面BDE; (2)求证:AF⊥面BDE.
如图,平行四边形ABCD的顶点A(-2,3),B(2,0),D(-4,0). (1)求平行四边形的边CD所在直线的方程; (2)求以B为圆心,且与对角线AC相切的圆的方程.
如图,在三棱柱ABC-A1B1C1中,E,F,G分别为B1C1,A1B1,AB的中点. (1)求证:平面A1C1G∥平面BEF; (2)若平面A1C1G∩BC=H,求证:H为BC的中点.
在平面直角坐标系xOy中,已知P是直线x-y+4=0上的一个动点,圆Q的方程为:(x-4)2+(y+4)2=9.设以线段PQ为直径的圆E与圆Q交于C,D两点. (1)证明:PC,PD均与圆Q相切; (2)当????=3
7
时,求点P的坐标; (3)求线段CD长度的最小值.
在平面直角坐标系xOy中,已知圆C:(x-a)2+y2=4,直线l:y=x+3. (1)当a=-1时,若圆C与直线l交于A,B两点,过点A,B分别作l的垂线与y轴交于D,E两点,求|DE|的值; (2)过直线l上的任意一点P作圆的切线PQ(Q为切点),若平面上总存在定点N,使得PQ=PN,求圆心C的横坐标的取值范围.
已知圆C过点(1,0),且与圆x2+(y-3)2=4外切于点(0,1),P(m,0)(m≠0)是x轴上的一个动点. (1)求圆C的标准方程; (2)当圆C上存在点Q,使∠CPQ=30°,求实数m的取值范围; (3)当m=1时,过P作直线PA,PB与圆C分别交于异于点P的点A,B两点,且kPA?kPB=-3.求证:直线AB恒过定点.
答案和解析
1.【答案】2x-y-2=0 【解析】
解:过点(1,0),且斜率为2的直线方程是 y-0=2(x-1), 化为一般式方程为2x-y-2=0. 故答案为:2x-y-2=0. 由题意写出直线的点斜式方程,再化为一般式方程. 本题考查了直线方程的应用问题,是基础题.
2.【答案】-1 【解析】
解:∵A(3,-2),B(-5,2),C(x,0)三点共线, ∴kAB=kAC,∴=, 解得x=-1. 故答案为:-1. A(3,-2),B(-5,2),C(x,0)三点共线,可得kAB=kAC,即可得出. 本题考查了三点共线与斜率之间的关系,考查了推理能力与计算能力,属于基础题.
3.【答案】四 【解析】
解:圆(x-a)2+(y-b)2=r2(r>0)的圆心位于第一象限, 则a>0且b>0, 直线y=ax+b的大致图象如图所示, 由此知该直线不经过第四象限. 故答案为:四. 根据题意知a>0且b>0,由此判断直线y=ax+b的图象不经过第四象限. 本题考查了圆的标准方程与直线方程的应用问题,是基础题.
4.【答案】-2<a<2 【解析】
解:点P(2a,a)在圆(x-a)2+(y+a)2=20的内部, 则(2a-a)2+(a+a)2<20, 解得-2<a<2, ∴实数a的取值范围是-2<a<2. 故答案为:-2<a<2. 根据点到圆心的距离|d|<r列不等式求得a的取值范围. 本题考查了点与圆的位置关系应用问题,是基础题.
5.【答案】x2+(y-1)2=4 【解析】
解:根据题意,设圆心的坐标为(m,n), 若圆心与点(1,0)关于直线y=x对称,则=且=-1, 解可得:m=0,n=1, 即圆心的坐标为(0,1), 又由圆C的半径为2,则圆C的标准方程为x2+(y-1)2=4; 故答案为:x2+(y-1)2=4. 根据题意,设圆心的坐标为(m,n),由圆心C与点(1,0)关于直线y=x对称,可得=且=-1,解可得m、n的值,即可得圆心的坐标,结合圆的标准方程,分析可得答案. 本题考查圆的标准方程,关键是求出圆心的坐标,属于基础题.
6.【答案】1 【解析】
解: 得:m=1 故答案是1 由两直线平行的充要条件求得. 本题主要考查两直线的位置关系.
7.【答案】
3
【解析】
解:设圆锥母线长为l,圆锥底面半径为r, ∵将一个底面半径为1的圆锥侧面沿一条母线展开,其展开图是半圆, 2π×1=π, 解得l=2, ∴该圆锥的高为:h==. 故答案为:. 设圆锥母线长为l,圆锥底面半径为r,由将一个底面半径为1的圆锥侧面沿一条母线展开,其展开图是半圆,求出l=2,从而该圆锥的高为:h=,由此能求出结果. 本题考查圆锥的高的求法,考查空间中线线、线面、面面间的位置关系等基础知识,考查运算求解能力,是基础题.
8.【答案】88 【解析】
解:设长方体的过一个顶点的三条棱长分别为a,2a,3a, 则,即14a2=56,得a=2. ∴长方体的过一个顶点的三条棱长分别为2,4,6. ∴这个长方体的表面积是2(2×4+2×6+4×6)=88. 故答案为:88. 设长方体的过一个顶点的三条棱长分别为a,2a,3a,可得,求得a值,得到长方体的过一个顶点的三条棱长,则答案可求. 本题考查棱柱表面积的求法,考查正方体体对角线与过一个顶点的三条棱的关系,是基础题.
9.【答案】-2 【解析】
解:把圆的方程化为标准方程得:(x+2)2+y2=5,则圆心坐标为(-2,0), 则过圆心与P直线的斜率k==-2,而直线ax+by+7=0的斜率为-, 所以-2?(-)=-1,化简得:2a=-b①, 又把P点坐标代入ax+by+7=0得:-3a+2b+7=0②, 把①代入②解得a=1,把a=1代入①解得b=-2, 则ab=-2. 故答案为:-2. 把圆的方程化为标准方程后,找出圆心坐标,根据切线垂直于过切点的直径,利用两直线垂直时斜率的乘积为-1,所以由圆心和P的坐标求出过这两点直线方程的斜率,根据已知直线的方程表示出斜率,两者相乘等于-1列出a与b的方程,记作①,又因为P在直线上,把P的坐标代入已知直线的方程,得到关于a与b的又一方程,记作②,两个方程联立即可求出a与b的值,求出ab即可. 此题考查学生掌握圆的切线垂直于过切点的直径,掌握两直线垂直时斜率的乘积为-1,会把圆的方程化为标准式方程并找出圆心的坐标,进而求解.
10.【答案】3 【解析】
解:由m,n为不重合的两条直线,α,β为不重合的两个平面,知: 在①中,若m∥α,n∥α,则m与n相交、平行或异面,故①错误; 在②中,若m⊥α,m⊥β,则由面面平行的判定定理得α∥β,故②正确; 在③中,若m∥α,m⊥β,则由面面垂直的判定定理得α⊥β,故③正确; 在④中,无论平行α与β相交不是平行,一定存在直线l,使得l∥α,l∥β,故④正确. 故答案为:3. 在①中,m与n相交、平行或异面;在②中,由面面平行的判定定理得α∥β;在③中,由面面垂直的判定定理得α⊥β;在④中,无论平行α与β相交不是平行,一定存在直线l,使得l∥α,l∥β. 本题考查命题真假的判断,考查空间中线线、线面、面面间的位置关系等基础知识,考查运算求解能力,是中档题.
11.【答案】x=1或3x+4y-5=0 【解析】
解:由题意可得,当直线l的斜率不存在时,直线方程为x=1,满足弦长为; 当直线l的斜率存在时,设直线方程为y-=k(x-1),即2kx-2y-2k+1=0. 圆x2+y2=4的半径为2,直线l被圆所截弦长为, 则圆心到直线的距离d=, 解得:k=. ∴直线l的方程为,即3x+4y-5=0. ∴直线l的方程为:x=1或3x+4y-5=0. 故答案为:x=1或3x+4y-5=0. 当直线l的斜率不存在时,直线方程为x=1,满足弦长为;当直线l的斜率存在时,设直线方程为y-=k(x-1),利用垂径定理结合点到直线的距离公式列式求得k值,则直线方程可求. 本题考查直线与圆位置关系,考查点到直线距离公式的应用,是基础题.
12.【答案】
3
2
【解析】
解:∵点A、C到BD的距离之比为3:2, ∴△BCD和△ABD的面积之比为3:2,可得S△BCD=S△ABD ∵AE=AA1,CF=CC1,∴ ∵三棱锥E-BCD的体积V1=S△BCD?AE,三棱锥F-ABD的体积V2=S△ABD?CF ∴===?=?= 故答案为: 根据A、C到BD的距离之比算出S△BCD=S△ABD.由直四棱柱ABCD-A1B1C1D1 中,AE=AA1且CF=CC1,算出AE=CF,再由锥体的体积公式加以计算即可得到的值. 本题给出直棱棱柱上满足条件的点,求两个三棱锥的体积之比.着重考查了直棱柱的性质、三角形的面积比和锥体的体积公式等知识,属于中档题.
13.【答案】(2,2) 【解析】
解:如图, 设B(4cosθ,4sinθ),M(x,y), ∵A(2,2),且, ∴(x,y)=(4cosθ+2,4sinθ+2), 则,即(x-2)2+(y-2)2=16. ∴M到N(2,2)的距离为定长, ∴点N的坐标是(2,2). 故答案为(2,2). 设B(4cosθ,4sinθ),M(x,y),又A(2,2),结合可得,消去参数得答案. 本题考查平面向量的坐标运算,考查圆的参数方程,是中档题.
14.【答案】12 【解析】
解:由题意平面α⊥平面β,A、B是平面α与平面β的交线上的两个定点,DA?β,CB?β,且DA⊥α,CB⊥α, ∴△PAD与△PBC是直角三角形,又∠APD=∠BPC, ∴△PAD∽△PBC,又AD=4,BC=8, ∴PB=2PA 作PM⊥AB,垂足为M,令AM=t∈R, 在两个Rt△PAM与Rt△PBM中,AM是公共边及PB=2PA ∴PA2-t2=4PA2-(6-t)2 解得PA2=12-4t ∴PM=, ∴S=×AB×PM==3=3≤12, ∴△PAB的面积的最大值为12. 故答案为:12. 本题在二面角背景下求三角形的面积,需要借助直二面角的相关知识研究三角形的几何特征,再由面积公式求出面积,由题设条件知两个直角三角形△PAD与△PBC是相似的直角三角形,根据题设条件可得出PB=2PA,作PD⊥AB,垂足为D,令AD=t,将三角形的面积用t表示出来,再研究面积的最值选出正确选项. 本题考查三角形的面积的最大值的求法,考查空间中线线、线面、面面间的位置关系等基础知识,考查运算求解能力,是中档题.
15.【答案】证明:(1)设AC∩BD=O,连结OE, 则O是AC的中点, ∵E是PA的中点,∴OE∥PC, ∵PC?平面BDE,OE?平面BDE, ∴PC∥面BDE. (2)∵底面ABCD为菱形,且PA⊥底面ABCD,AF⊥PC, ∴BD⊥AC,BD⊥PD, ∴BD⊥平面PAC,∴BD⊥AF, ∵BD⊥AF,AF⊥PC,PC∩AF=F, ∴AF⊥平面PBD,∴AF⊥OE, ∵OE∩BD=E,∴AF⊥面BDE. 【解析】
(1)设AC∩BD=O,连结OE,推导出OE∥PC,由此能证明PC∥面BDE. (2)推导出AF⊥PC,BD⊥AC,BD⊥PD,从而BD⊥平面PAC,进而BD⊥AF,再求出AF⊥OE,由此能证明AF⊥面BDE. 本题考查线面平行、线面垂直的证明,考查空间中线线、线面、面面间的位置关系等基础知识,考查运算求解能力,考查函数与方程思想,是中档题.
16.【答案】解:(1)设C(a,b), ∵A(-2,3),B(2,0),D(-4,0), ∴
????
=(4,?3),
????
=(??+4,??), 则
?3=??
4=??+4
,即a=0,b=-3,则C(0,-3). ∴CD所在直线方程为
??
?4
+
??
?3
=1,即3x+4y+12=0; (2)
??
????
=
?3?3
0?(?2)
=?3,则AC:y=-3x-3,即3x+y+3=0. ∴B到直线AC的距离d=
|2×3+3|
9+1
=
9
10
. ∴以B为圆心,且与对角线AC相切的圆的方程为(???2
)
2
+
??
2
=
81
10
. 【解析】
(1)设C(a,b),求得,利用向量相等求解; (2)求出AC所在直线方程,再求出B到AC的距离,代入圆的标准方程得答案. 本题考查利用向量的坐标运算求解点的坐标,考查直线方程的应用,考查点到直线的距离公式,是基础题.
17.【答案】证明:(1)如图, ∵E,F分别为B1C1,A1B1的中点,∴EF∥A1C1, ∵A1C1?平面A1C1G,EF?平面A1C1G,∴EF∥平面A1C1G, 又F,G分别为A1B1,AB的中点,∴A1F=BG, 又A1F∥BG,∴四边形A1GBF为平行四边形,则BF∥A1G, ∵A1G?平面A1C1G,BF?平面A1C1G,∴BF∥平面A1C1G, 又EF∩BF=F, ∴平面A1C1G∥平面BEF; (2)∵平面ABC∥平面A1B1C1,平面A1C1G∩平面A1B1C1=A1C1, 平面A1C1G与平面ABC有公共点G,则有经过G的直线,设交BC=H, 则A1C1∥GH,得GH∥AC, ∵G为AB的中点,∴H为BC的中点. 【解析】
(1)由已知可得EF∥A1C1,得到EF∥平面A1C1G,同理得到BF∥平面A1C1G,再由面面平行的判定可得平面A1C1G∥平面BEF; (2)由公理3及平面与平面平行的性质得A1C1∥GH,则GH∥AC,由G为AB的中点,可得H为BC的中点. 本题考查平面与平面平行的判定,考查面面平行的性质,考查空间想象能力与思维能力,是中档题.
18.【答案】解:(1)证明:根据题意,连接CQ、CD, 圆E是以线段PQ为直径的圆,则∠PCQ=∠PDQ=90°,即PC⊥CQ,PD⊥DQ, 又由C、D都在圆Q上, 则PC,PD均与圆Q相切; (2)根据题意,设P(m,m+4), 圆Q的方程为:(x-4)2+(y+4)2=9,圆心Q(4,-4),半径r=3, 当????=3
7
时,|PQ|2=PC2+CQ2=63+9=72, 则有(m-4)2+(m+8)2=72,即m2+4m+4=0 解可得:m=-2, 则P的坐标为(-2,2); (3)根据题意,设PQ=t,则PC=
??
2
?9
, 则CD=2×
????×????
????
=6
1?
9
??
2
, 分析可得:当t取得最小值时,CD的值最小, 当PQ与直线x-y+4=0垂直时,PQ最小,且PQ的最小值为
|4?(?4)+4|
1+1
=6
2
, 此时CD取得最小值,且其最小值为6×
1?
1
(6
2
)
2
=
3
14
2
. 【解析】
(1)根据题意,连接CQ、CD,分析易得PC⊥CQ,PD⊥DQ,又由C、D都在圆Q上,即可得证明; (2)根据题意,设P(m,m+4),由直线与圆的位置关系可得|PQ|2=PC2+CQ2=63+9=72,由两点间距离公式可得(m-4)2+(m+8)2=72,解可得m的值,即可得答案; (3)根据题意,设PQ=t,求出PC的值,据此可得CD=2×=6,分析可得当t取得最小值时,CD的值最小,进而可得当PQ与直线x-y+4=0垂直时,PQ最小,计算即可得答案. 本题考查直线与圆的方程的综合应用,涉及直线与圆的位置关系,属于基础题.
19.【答案】解:(1)a=-1时,圆C:(x+1)2+y2=4, 与直线l:y=x+3的交点A(-3,0),B(-1,2), ∴直线AD:y=-x-3,直线BE:y=-x+1, 令x=0,分别得y=-3,y=1, ∴D(0,-3),E(0,1). ∴|DE|=4; (2)设P(m,m+3),定点N(x0,y0), 由题意可得,PQ⊥CQ, ∴|PQ|2=|PC|2-|CQ|2=(m-a)2+(m+3-0)2-4, |PN|2=(m-x0)2+(m+3-y0)2, 依题意对任意的m, 都有|PQ|2=|PN|2?(m-a)2+(m+3-0)2-4=(m-x0)2+(m+3-y0)2 ?(2x0+2y0-2a)m=
??
0
2
+
??
0
2
-6y0+4-a2成立, ∴
2
??
0
+2
??
0
?2??=0
??
0
2
+
??
0
2
?6
??
0
+4?
??
2
=0
,消去x0并整理得:
??
0
2
-(3+a)y0+2=0对y0有解, 所以△=(3+a)2-4×2≥0,解得:a≤?3?2
2
或a≥?3+2
2
故圆心C的横坐标a的取值范围是:(-∞,-3-2
2
]∪[-3+2
2
,+∞). 【解析】
(1)当a=-1时,联立直线与圆的方程求出A,B的坐标,再求出D,E的坐标,就可以算出|DE|; (2)设出P(m,m+3),N(x0,y0),由PQ=PN得|PQ|2=|PN|2,得|PC|2-4=|PN|2,再将此式坐标化,然后先对m恒成立,在对y0有解,就可以求出a的取值范围了. 本题考查了直线和圆的方程的应用.属难题.
20.【答案】(1)解:设圆C:x2+(y-b)2=r2, 则
0
2
+(1???
)
2
=
??
2
1
2
+(0???
)
2
=
??
2
,解得,b=0,r=1, 故圆C的标准方程为:x2+y2=1; (2)解:当圆C上存在点Q,使∠CPQ=30°,等价于直线y=
3
3
(x-m)与圆C有交点, ∴圆C到直线
3
x-3y-
3
m=0的距离小于等于半径1, 即
3
|??|
3+9
≤1,解得-2≤m≤2, 故实数m的取值范围是[-2,2]; (3)证明:m=1时,P(1,0),设kPA=k,则kPB=?
3
??
, 则直线PA:y=k(x-1),PB:y=?
3
??
(???1), 联立
??
2
+
??
2
=1
??=??(???1)
,得(1+k2)x2-2k2x+k2-1=0, 则
??
??
+1=
2
??
2
1+
??
2
,得
??
??
=
2
??
2
1+
??
2
?1=
??
2
?1
1+
??
2
,
??
??
=??(
??
??
?1)=
?2??
1+
??
2
. ∴A(
??
2
?1
1+
??
2
,
?2??
1+
??
2
). 同理可得B(
9?
??
2
??
2
+9
,
6??
??
2
+9
). 则
??
????
=
6??
??
2
+9
+
2??
??
2
+1
9?
??
2
??
2
+9
?
??
2
?1
??
2
+1
=
4
??
3
+12??
9?
??
4
. ∴直线AB的方程为??+
2??
??
2
+1
=
4
??
3
+12??
9?
??
4
(???
??
2
?1
1+
??
2
).(*) 当k=1时,直线方程为y=2x-1,当k=-1时,直线方程为y=-2x+1. 联立
??=?2??+1
??=2???1
,解得x=
1
2
,y=0. 把点(
1
2
,0)代入(*)成立, ∴直线AB恒过定点(
1
2
,0). 【解析】
(1)设出圆的标准方程x2+(y-b)2=r2,由已知可得关于r,b的方程组求解得答案; (2)把圆C上存在点Q,使∠CPQ=30°,转化为直线y=(x-m)与圆C有交点,由圆心到直线的距离小于半径求解; (3)m=1时,P(1,0),设kPA=k,则kPB=,可得直线PA,PB的方程,与圆的方程联立,求得A,B的坐标,写出AB所在直线方程,分别取k=1和-1,得到直线方程,联立求得交点坐标,再代回直线方程验证得答案. 本题考查圆的标准方程的求法,考查直线与圆位置关系的应用,考查直线恒过定点问题,考查计算能力,是难题.
同课章节目录
