华师大九年级下期末专题《第26章二次函数》单元检测试卷含解析
文档属性
| 名称 | 华师大九年级下期末专题《第26章二次函数》单元检测试卷含解析 |

|
|
| 格式 | zip | ||
| 文件大小 | 245.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-01-18 00:00:00 | ||
图片预览




文档简介
华师大版九年级数学下册期末专题: 第26章 二次函数 单元检测试卷
一、单选题(共10题;共30分)
1.将抛物线y=-2x2+1向右平移1个单位,再向上平移2个单位后所得到的抛物线为(?? )
A.?y=-2(x+1)2-1?????????/B.?y=-2(x+1)2+3?????????/C.?y=-2(x-1)2+1?????????/D.?y=-2(x-1)2+3
2.已知关于x的函数y=(m﹣1)xm+(3m+2)x+1是二次函数,则此解析式的一次项系数是(?? )
A.?﹣1?????????????????????????????????????????/B.?8?????????????????????????????????????????/C.?﹣2?????????????????????????????????????????/D.?1
3.把抛物线y=-2x2先向右平移1个单位长度,再向上平移2个单位长度后,所得函数的表达式为( ??)
A.?y=-2(x+1)2+2??????????/B.?y=-2(x+1)2-2??????????/C.?y=-2(x-1)2+2??????????/D.?y=-2(x-1)2-2
4.如图所示是一个抛物线形桥拱的示意图,在所给出的平面直角坐标系中,当水位在AB位置时,水面宽度为10m,此时水面到桥拱的距离是4m,则抛物线的函数关系式为(??? )
/
A.?y=
25
4
??
2
?????????????????????????/B.?y=﹣
25
4
??
2
?????????????????????????/C.?y=﹣
4
25
??
2
?????????????????????????/D.?y=
4
25
??
2
5.已知二次函数y=ax2+bx+c的图象如图所示,则下列结论中:①ac>0;②a+b+c<0;③4a﹣2b+c<0;④2a+b<0;⑤4ac﹣b2<4a;⑥a+b>0中,其中正确的个数为(?? )
/
A.?2???????????????????????????????????????????/B.?3???????????????????????????????????????????/C.?4???????????????????????????????????????????/D.?5
6.已知二次函数 ??=
??
2
+??+?? ,当 ?? 取任意实数时,都有 ??>0 ,则 ?? 的取值范围是(??? ).
A.??≥
1
4
B.??>
1
4
C.??≤
1
4
D.??<
1
4
7.下列关系式中,属于二次函数的是(x是自变量)( )
A.?y=
1
3
??
2
???????????????????????????/B.?y=
??
2
?1
???????????????????????????/C.?y=
1
??
2
???????????????????????????/D.?y=ax2+bx+c
8.已知二次函数 ??=??
??
2
+????+??(??≠0) 的图象如图所示,有下列4个结论,其中正确的结论是( ??) /
A.???????>0?????????????????????????B.?2?????=0?????????????????????????C.???>??+???????????????????????????D.?
??
2
?4????<0 ?
9.若A(-4,y1),B(-3,y2),C(1,y3)为二次函数y=x2+4x-m的图象上的三点,则y1 , y2 , y3的大小关系是(?? )
A.y1<y2<y3 B.y2<y1<y3 C.y3 <y1<y2 D.y1<y3<y2
10.抛物线y=ax2+bx+c的图角如图,则下列结论:①abc>0;②a+b+c=2;③a<
1
2
;④b>1.其中正确的结论是( ) /
A.?①②?????????????????????????????????????B.?②③?????????????????????????????????????C.?②④?????????????????????????????????????D.?③④
二、填空题(共10题;共30分)
11.把抛物线 ??=
(???1)
2
+2 沿x轴向左平移4个单位,再沿y轴向上平移3个单位后,所得新抛物线相应的函数表达式是________.
12.若抛物线y=x2-2x-3与x轴分别交于A,B两点,则AB的长为 ________.
13.如果抛物线y=2x2与抛物线y=ax2关于x轴对称,那么a的值是________.
14.若二次函数y=ax2+bx+c(a≠0)的图象与x轴有两个交点,坐标分别为(x1 , 0)、(x2 , 0),且x1<x2 , 图象上有一点M(x0 , y0)在x轴下方,在下列四个算式中判定正确的是________ ?①a(x0﹣x1)(x0﹣x2)<0;②a>0;③b2﹣4ac≥0;④x1<x0<x2 .
15.抛物线y=x2﹣6x+5向上平移2个单位长度,再向右平移1个单位长度后,得到的抛物线解析式是________?.
16.如图,边长为1的正方形ABCO,以A为顶点,且经过点C的抛物线与对角线交于点D,点D的坐标为________. /
17.如图,二次函数y=x2﹣6x+5的图象交x轴于A、B两点,交y轴于点C,则△ABC的面积为________?. ?/
18.将抛物线 ??=2
(???1)
2
+4 ,绕着它的顶点旋转
180
°
,旋转后的抛物线表达式是________.
19.将抛物??=?
???1
2
向左平移1个单位后,得到的抛物线的解析式是________.
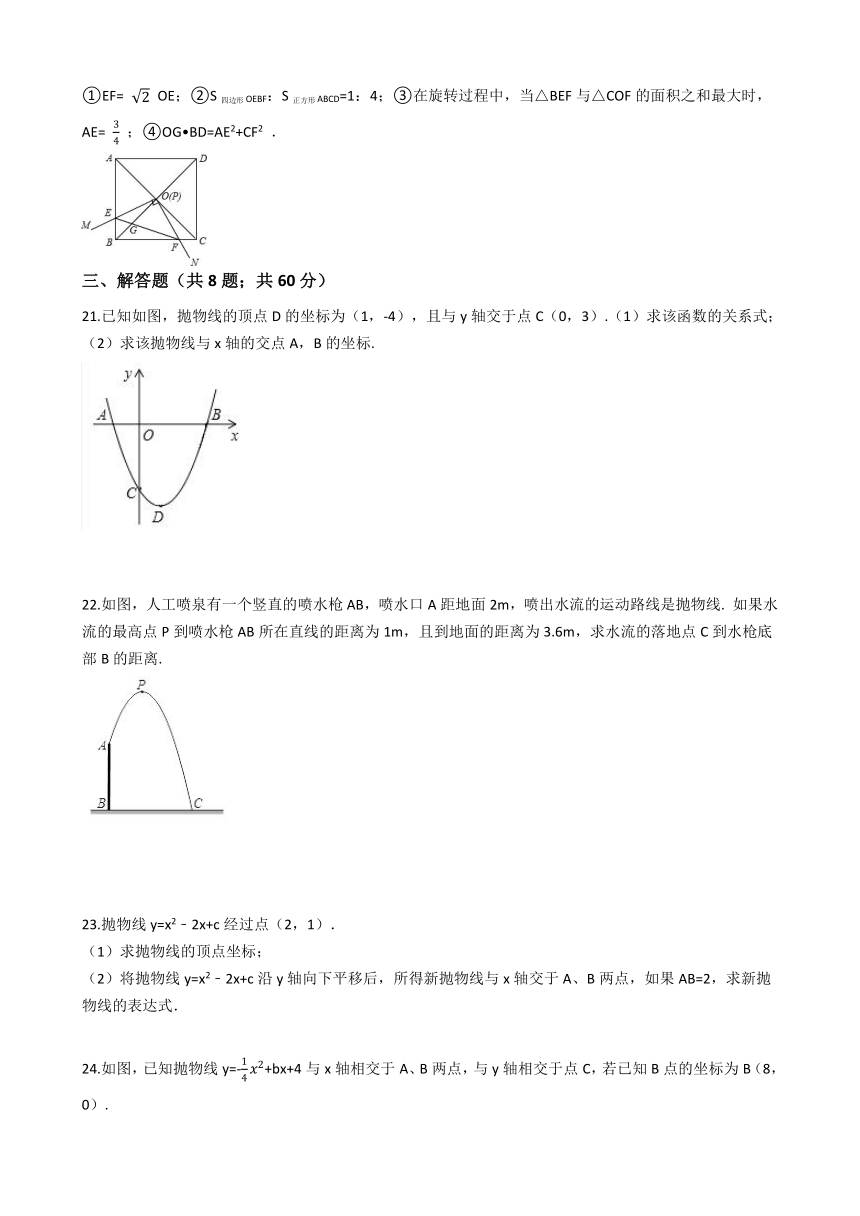
20.如图,边长为1的正方形ABCD的对角线AC,BD相交于点O,直角∠MPN的顶点P与点O重合,直角边PM,PN分别与OA,OB重合,然后逆时针旋转∠MPN,旋转角为θ(0°<θ<90°),PM、PN分别交AB、BC于E、F两点,连接EF交OB于点G,则下列结论中正确的是________. ①EF=
2
OE;②S四边形OEBF:S正方形ABCD=1:4;③在旋转过程中,当△BEF与△COF的面积之和最大时,AE=
3
4
;④OG?BD=AE2+CF2 . /
三、解答题(共8题;共60分)
21.已知如图,抛物线的顶点D的坐标为(1,-4),且与y轴交于点C(0,3).(1)求该函数的关系式;(2)求该抛物线与x轴的交点A,B的坐标. /
22.如图,人工喷泉有一个竖直的喷水枪AB,喷水口A距地面2m,喷出水流的运动路线是抛物线. 如果水流的最高点P到喷水枪AB所在直线的距离为1m,且到地面的距离为3.6m,求水流的落地点C到水枪底部B的距离. /
23.抛物线y=x2﹣2x+c经过点(2,1). (1)求抛物线的顶点坐标; (2)将抛物线y=x2﹣2x+c沿y轴向下平移后,所得新抛物线与x轴交于A、B两点,如果AB=2,求新抛物线的表达式.
24.如图,已知抛物线y=-
1
4
??
2
+bx+4与x轴相交于A、B两点,与y轴相交于点C,若已知B点的坐标为B(8,0). / (1)求抛物线的解析式及其对称轴方程; (2)连接AC、BC,试判断△AOC与△COB是否相似?并说明理由; (3)M为抛物线上BC之间的一点,N为线段BC上的一点,若MN∥y轴,求MN的最大值; (4)在抛物线的对称轴上是否存在点Q,使△ACQ为等腰三角形?若存在,求出符合条件的Q点坐标;若不存在,请说明理由.
25.已知二次函数图象顶点为C(1,0),直线y=x+m与该二次函数交于A,B两点,其中A点(3,4),B点在y轴上. / (1)求此二次函数的解析式; (2)P为线段AB上一动点(不与A,B重合),过点P作y轴的平行线与二次函数交于点E.设线段PE长为h,点P横坐标为x,求h与x之间的函数关系式; (3)D为线段AB与二次函数对称轴的交点,在AB上是否存在一点P,使四边形DCEP为平行四边形?若存在,请求出P点坐标;若不存在,请说明理由.
26.如图,在平面直角坐标系中,二次函数y=x2+bx+c的图象与x轴交于A、B两点,A点在原点的左侧,B点的坐标为(3,0),与y轴交于C(0,﹣3)点,点P是直线BC下方的抛物线上一动点. / (1)求这个二次函数的表达式. (2)连接PO、PC,并把△POC沿CO翻折,得到四边形POP′C,那么是否存在点P,使四边形POP′C为菱形?若存在,请求出此时点P的坐标;若不存在,请说明理由. (3)当点P运动到什么位置时,四边形ABPC的面积最大?求出此时P点的坐标和四边形ABPC的最大面积.
27.如图1,已知二次函数y=ax2+bx+c(a、b、c为常数,a≠0)的图象过点O(0,0)和点A(4,0),函数图象最低点M的纵坐标为﹣
8
3
,直线l的解析式为y=x.
/
(1)求二次函数的解析式;
(2)直线l沿x轴向右平移,得直线l′,l′与线段OA相交于点B,与x轴下方的抛物线相交于点C,过点C作CE⊥x轴于点E,把△BCE沿直线l′折叠,当点E恰好落在抛物线上点E′时(图2),求直线l′的解析式;
(3)在(2)的条件下,l′与y轴交于点N,把△BON绕点O逆时针旋转135°得到△B′ON′,P为l′上的动点,当△PB′N′为等腰三角形时,求符合条件的点P的坐标.
28.如图, 四边形OABC为直角梯形,A(4,0),B(3,4),C(0,4). 点M从O 出发以每秒2个单位长度的速度向A运动;点N从B同时出发,以每秒1个单位长度的速度向C运动.其中一个动点到达终点时,另一个动点也随之停止运动.过点N作NP垂直/轴于点P,连结AC交NP于Q,连结MQ. / (1)点?????(填M或N)能到达终点; (2)求△AQM的面积S与运动时间t的函数关系式,并写出自变量t的取值范围,当t为何值时,S的值最大; (3)是否存在点M,使得△AQM为直角三角形?若存在,求出点M的坐标,若不存在, 说明理由.//
答案解析部分
一、单选题
1.【答案】D
【考点】二次函数图象的几何变换
【解析】【解答】根据左加右减,上加下减的归则.将抛物线y=-2x2+1向右平移1个单位得y=-2(x-1)2+3,再向上平移2个单位得y=-2(x-1)2+3.故答案为:D.
【分析】根据平移规律“左加右减,上加下减“”即可求解。
2.【答案】B
【考点】二次函数的定义
【解析】【解答】解:∵关于x的函数y=(m﹣1)xm+(3m+2)x+1是二次函数,∴m=2, 则3m+2=8, 故此解析式的一次项系数是:8. 故答案为:B 【分析】根据二次函数的定义,自变量的最高次数是2,得出m的值,再将m的值代入3m+2即可算出一次项的系数。
3.【答案】C
【考点】二次函数图象的几何变换
【解析】【解答】解:把抛物线y=-2x2先向右平移1个单位长度,再向上平移2个单位长度后,所得函数的表达式为y=-2(x-1)2+2,故答案为:C. 【分析】根据函数平移的特点“上加下减,左加右减”,向右平移一个单位,x减去1,向上平移2个单位,函数解析式末尾加上2。
4.【答案】C
【考点】待定系数法求二次函数解析式
【解析】【解答】如图,由题意可设抛物线的解析式为 ??=??
??
2
,∵由题意可知点A、B的坐标分别为(-5,-4)、(5,-4),且抛物线过点A、B, ∴ 25??=?4 ,解得: ??=?
4
25
, ∴抛物线的解析式为:y=?
4
25
x2 故答案为:C. 【分析】先设抛物线为 y=ax2 , 根据题意可得出A、B的坐标分别为 (-5,-4)、(5,-4),将A、B的坐标代入 y=ax2 , 解出a,即为所求解析式。
5.【答案】C
【考点】二次函数图象与系数的关系
【解析】【解答】解:解:①图象开口向下,与y轴交于负半轴,对称轴在y轴右侧,能得到:a<0,c<0, ∴ac>0,故①正确;②当x=1时,y>0,∴a+b+c>0,故②错误;③当x=﹣2时,y<0,∴4a﹣2b+c<0,故③正确;④∵对称轴x=﹣
??
2??
<1, ∴2a+b>0,故④错误;⑤∵抛物线的顶点在x轴的上方, ∴
4?????
??
2
4??
>0, ∴4ac﹣b2<4a,故⑤正确;⑥∵2a+b>0, ∴2a+b﹣a>﹣a, ∴a+b>﹣a, ∵a<0, ∴﹣a>0, ∴a+b>0,故⑥正确; 综上所述正确的个数为4个, 故选:C. / 【分析】由抛物线的开口方向判断a与0的关系,由抛物线与y轴的交点判断c与0的关系,然后根据对称轴及抛物线的顶点坐标情况进行推理,进而对所得结论进行判断.
6.【答案】B
【考点】二次函数图象与系数的关系
【解析】【解答】已知二次函数的解析式为:y=x2+x+m,
∴函数的图象开口向上,
又∵当x取任意实数时,都有y>0,
∴有△<0,
∴△=1-4m<0,
∴m>
1
4
,
故答案为:B.
【分析】二次函数图像开口向上,故y>0即为函数与x轴无交点,那么只需所对应的一元二次方程没有实数根.
7.【答案】A
【考点】二次函数的定义
【解析】【解答】解:A、是二次函数,故A正确; B、不是二次函数的形式,故B错误; C、是分式,故C错误; D、a=0是一次函数,故D错误; 故选:A. 【分析】根据函数y=ax2+bx+c (a≠0)是二次函数,可得答案.
8.【答案】C
【考点】二次函数的图象,二次函数的性质,二次函数图象与系数的关系,抛物线与x轴的交点,二次函数图象上点的坐标特征
【解析】【解答】抛物线的开口向下,则a<0;…① 抛物线的对称轴为x=1,则-
??
2??
=1,b=-2a;…② 抛物线交y轴于正半轴,则c>0;…③ 抛物线与x轴有两个不同的交点,则:△=b2-4ac>0; 由②知:b>0,b+2a=0; 又由①③得:abc<0; 由图知:当x=-1时,y<0;即a-b+c<0,b>a+c; 故答案为:C. 【分析】根据抛物线的开口方向,对称轴的位置及抛物线与y轴的交点情况,可知a<0、c>0、b>0,即可对A作出判断;根据对称轴x=1,可得出b+2a=0,可对B作出判断;将b > a + c变形为a-b+c<0,根据x=-1,即可作出判断;根据抛物线与x轴的交点个数可对D作出判断。
9.【答案】B
【考点】二次函数y=ax^2+bx+c的性质
【解析】【解答】根据二次函数的解析式可知其对称轴为x= ?
??
2??
=-2,然后根据二次函数的图像可知开口向上,因此根据二次函数的增减性,可知y2<y1<y3.
故答案为:B
【分析】先求出抛物线的对称轴,再根据二次函数的图像可知开口向上,然后利用二次函数的增减性,可得出答案。
10.【答案】C
【考点】二次函数图象与系数的关系
【解析】
【分析】由抛物线的开口方向判断a与0的关系,由抛物线与y轴的交点判断c与0的关系,然后根据对称轴及抛物线与x轴交点情况进行推理,进而对所得结论进行判断.
【解答】①∵抛物线的开口向上,∴a>0, ∵与y轴的交点为在y轴的负半轴上,∴c<0, ∵对称轴为x=-
??
2??
<0,∴a、b同号,即b>0, ∴abc<0, 故本选项错误; ②当x=1时,函数值为2, ∴a+b+c=2; 故本选项正确; ③∵对称轴x=-
??
2??
>-1, 解得:
??
2
<a, ∵b>1, ∴a>
1
2
, 故本选项错误; ④当x=-1时,函数值<0, 即a-b+c<0,(1) 又a+b+c=2, 将a+c=2-b代入(1), 2-2b<0, ∴b>1 故本选项正确; 综上所述,其中正确的结论是②④; 故选C.
【点评】二次函数y=ax2+bx+c系数符号的确定: (1)a由抛物线开口方向确定:开口方向向上,则a>0;否则a<0. (2)b由对称轴和a的符号确定:由对称轴公式x=-
??
2??
判断符号. (3)c由抛物线与y轴的交点确定:交点在y轴正半轴,则c>0;否则c<0. (4)b2-4ac的符号由抛物线与x轴交点的个数确定:2个交点,b2-4ac>0;1个交点,b2-4ac=0;没有交点,b2-4ac<0. (5)当x=1时,可确定a+b+c的符号,当x=-1时,可确定a-b+c的符号. (6)由对称轴公式x=-
??
2??
, 可确定2a+b的符号
二、填空题
11.【答案】/
【考点】二次函数图象的几何变换
【解析】【解答】把抛物线 ??=
(???1)
2
+2 沿x轴向左平移4个单位得 ??=
(??+3)
2
+2 ,再沿y轴向上平移3个单位后得 ??=
(??+3)
2
+5 .
故答案为: ??=
(??+3)
2
+5 .
【分析】根据抛物线的几何变换规律,在顶点式的完全平方式内左加右减,在顶点式的常数项处上加下减,即可得出平移后新函数的函数解析式。
12.【答案】4
【考点】二次函数图像与坐标轴的交点问题
【解析】【解答】二次函数y=x2-2x-3与x轴交点A、B的横坐标为一元二次方程x2-2x-3=0的两个根,求得x1=-1,x2=3,则AB=|x2-x1|=4.【分析】先令y=0求出二次函数与x轴的交点A、B,两个交点的横坐标x1、x2 之间的距离即为AB的长。
13.【答案】-2
【考点】二次函数y=ax^2的图像
【解析】【解答】根据关于x轴对称的抛物线的开口方向改变,开口大小不变,可由抛物线y=2x2与抛物线y=ax2关于x轴对称,知两抛物线开口大小不变,方向相反,因此可得a=﹣2. 故答案为:﹣2. 【分析】根据关于x轴对称的抛物线的开口方向改变,开口程度不变可得a=﹣2。
14.【答案】①
【考点】二次函数图象与系数的关系,抛物线与x轴的交点
【解析】【解答】解: ∵二次函数y=ax2+bx+c(a≠0)的图象与x轴有两个交点无法确定a的正负情况, ∴选项②项错误; ∵二次函数y=ax2+bx+c(a≠0)的图象与x轴有两个交点,且坐标分别为(x1 , 0)、(x2 , 0),且x1<x2 , ∴b2﹣4ac>0,故选项③错误; 若a>0,则x1<x0<x2 , 若a<0,则x0<x1<x2或x1<x2<x0 , 故选项④错误 若a>0,则x0﹣x1>0,x0﹣x2<0, ∴(x0﹣x1)(x0﹣x2)<0, ∴a(x0﹣x1)(x0﹣x2)<0, 若a<0,则(x0﹣x1)与(x0﹣x2)同号, ∴a(x0﹣x1)(x0﹣x2)<0, 综上所述,a(x0﹣x1)(x0﹣x2)<0正确,故选项①正确, 故答案为:①. 【分析】根据抛物线与x轴有两个不同的交点,根的判别式△>0,再分a>0和a<0两种情况对各选项讨论即可得解.
15.【答案】y=(x﹣4)2﹣3
【考点】二次函数图象的几何变换
【解析】【解答】解:y=x2﹣6x+5=(x﹣3)2﹣4,其顶点坐标为(3,﹣4). 向上平移2个单位长度,再向右平移1个单位长度后的顶点坐标为(4,﹣3),得到的抛物线的解析式是y=(x﹣4)2﹣2, 故答案为:y=(x﹣4)2﹣2. 【分析】根据题意易得新抛物线的顶点,根据顶点式及平移前后二次项的系数不变可得新抛物线的解析式.
16.【答案】(
3?
5
2
,
3?
5
2
)
【考点】待定系数法求二次函数解析式,二次函数的应用,正方形的性质,二次函数与一次函数的综合应用
【解析】【解答】解:A的坐标是(1,0)、C坐标是(0,1),设出解析式是y=a(x﹣1)2 , 把C的坐标代入得:a(﹣1)2=1, 解得:a=1, 则抛物线的解析式是:y=(x﹣1)2; ∵B的坐标是(1,1), 设OB解析式的解析式是y=kx,则k=1,则OB的解析式是y=x. 根据题意得: {
??=
(???1)
2
??=??
, 解得: {
??=
3+
5
2
??=
3+
5
2
(舍去),或 {
??=
3?
5
2
??=
3?
5
2
. 则D的坐标是:(
3?
5
2
,
3?
5
2
). 故答案为:(
3?
5
2
,
3?
5
2
). 【分析】根据图形首先求得A、B、C的坐标,利用待定系数法即可求得抛物线的解析式和直线OB的解析式,然后两函数解析式联立组成的方程组即可求解。
17.【答案】10
【考点】二次函数图像与坐标轴的交点问题
【解析】【解答】解:在y=x2﹣6x+5中, 当y=0时,x=1或5; 当x=0时,y=5; 则A(1,0)、B(5,0)、C(0,5) 故△ABC的面积为:
1
2
×4×5=10; 故答案为:10. ?/ 【分析】根据解析式求出A、B、C三点的坐标,即△ABC的底和高求出,然后根据三角形的面积公式进行计算即可.
18.【答案】??=?2
(???1)
2
+4
【考点】二次函数图象的几何变换
【解析】【解答】解:抛物线 ??=2
(???1)
2
+4 的顶点为(1,4),
∵原抛物线是绕顶点(1,4)旋转,
∴旋转后的抛物线的顶点依然是(1,4).
∵旋转了180°,
∴原来开口向上变成开口向下,但开口形状不变,∴二次项系数为-2,
∴旋转后的抛物线表达式为 ??=?2
(???1)
2
+4 ,
故答案为: ??=?2
(???1)
2
+4
【分析】求抛物线的几何变化中的解析式,需要将解析式化成顶点式;根据顶点变化,及二次项系数的变化,可得到新的解析式.以顶点为中心旋转,∴顶点不变,但抛物线的开口方向变了.
19.【答案】??=
??
2
【考点】二次函数图象与几何变换
【解析】【解答】 ∵向左平移1个单位∴y=-(x-1+1)2=-x2 . 故得到的抛物线的解析式是y=-x2 . 【分析】根据二次函数图象的平移规律“上加下减,左加右减”进行解题.
20.【答案】①②④
【考点】二次函数的最值,全等三角形的判定与性质,相似三角形的判定与性质
【解析】【解答】解:①∵四边形ABCD是正方形, ∴OB=OC,∠OBE=∠OCF=45°,∠BOC=90°, ∴∠BOF+∠COF=90°, ∵∠EOF=90°, ∴∠BOF+∠COE=90°, ∴∠BOE=∠COF, 在△BOE和△COF中, {
∠??????=∠??????
????=????
∠??????=∠??????
, ∴△BOE≌△COF(ASA), ∴OE=OF,BE=CF, ∴EF=
2
OE;故正确; ②∵S四边形OEBF=S△BOE+S△BOE=S△BOE+S△COF=S△BOC=
1
4
S正方形ABCD , ∴S四边形OEBF:S正方形ABCD=1:4;故正确; ③过点O作OH⊥BC, / ∵BC=1, ∴OH=
1
2
BC=
1
2
, 设AE=x,则BE=CF=1﹣x,BF=x, ∴S△BEF+S△COF=
1
2
BE?BF+
1
2
CF?OH=
1
2
x(1﹣x)+
1
2
(1﹣x)×
1
2
=﹣
1
2
(x﹣
1
4
)2+
9
32
, ∵a=﹣
1
2
<0, ∴当x=
1
4
时,S△BEF+S△COF最大; 即在旋转过程中,当△BEF与△COF的面积之和最大时,AE=
1
4
;故错误; ④∵∠EOG=∠BOE,∠OEG=∠OBE=45°, ∴△OEG∽△OBE, ∴OE:OB=OG:OE, ∴OG?OB=OE2 , ∵OB=
1
2
BD,OE=
2
2
EF, ∴OG?BD=EF2 , ∵在△BEF中,EF2=BE2+BF2 , ∴EF2=AE2+CF2 , ∴OG?BD=AE2+CF2 . 故正确. 故答案为:①②④. 【分析】①根据全等三角形的定义,通过ASA判定得出△BOE≌△COF, 以此得出结论。 ②求证S四边形OEBF=S△BOC=
1
4
S正方形ABCD,得出结论。 ③设AE=x,则BE=CF=1﹣x,BF=x,表示出S△BEF+S△COF,求出S△BEF+S△COF最大时的x值。 ④证出△OEG∽△OBE,由相似三角形的对应边成比例,求证出OG?BD=AE2+CF2。
三、解答题
21.【答案】解:(1)∵抛物线的顶点D的坐标为(1,?4), ∴设抛物线的函数关系式为y=a(x?1)2?4, 又∵抛物线过点C(0,3), ∴3=a(0?1)2?4, 解得a=1, ∴抛物线的函数关系式为y=(x?1)2?4, 即y=x2?2x?3; ( 2 )令y=0,得:x2 ?2???3=0 , 解得
??
1
=3 ,
??
2
=?1 . 所以坐标为A(3,0),B(-1,0).
【考点】待定系数法求二次函数解析式,二次函数图像与坐标轴的交点问题
【解析】【分析】(1)设出抛物线方程的顶点式,将点C的坐标代入即可求得抛物线方程;(2)对该抛物线令y=0,解二元一次方程即可求得点A,B的坐标.
22.【答案】解:建立平面直角坐标系,如图, / 于是抛物线的表达式可以设为 ??=??
(????)
2
+?? ?, 根据题意,得出A,P两点的坐标分别为A(0,2),P(1,3.6), ∵点P为抛物线顶点, ∴ ?=1,??=3.6 ?, ∵点A在抛物线上, ∴ ??+3.6=2 , ??=?1.6 , ∴它的表达式为 ??=?1.6
(???1)
2
+3.6 , 当点C的纵坐标y=0时,有 ?1.6
(???1)
2
+3.6=0 ,
??
1
=?0.5 (舍去),
??
2
=2.5 , ∴BC=2.5, ∴水流的落地点C到水枪底部B的距离为2.5m
【考点】二次函数的图象,待定系数法求二次函数解析式,抛物线与x轴的交点,二次函数的应用
【解析】【分析】将实际问题转化为数学问题,根据喷水口A距地面2m,可得出点A的坐标为(0,2),根据水流的最高点P到喷水枪AB所在直线的距离为1m,且到地面的距离为3.6m,得出抛物线的顶点P的坐标为(1,3.6),因此设函数解析式为顶点式,再将点A的坐标代入即可求出函数解析式,然后由y=0建立方程求出x的值,根据实际情况取值即可。
23.【答案】解:(1)把(2,1)代入y=x2﹣2x+c得4﹣4+c=1,解得c=1, 所以抛物线解析式为y=x2﹣2x+1; (2)y=x2﹣2x+1=(x﹣1)2 , 抛物线的对称轴为直线x=1, 而新抛物线与x轴交于A、B两点,AB=2, 所以A(0,0),B(2,0), 所以新抛物线的解析式为y=x(x﹣2),即y=x2﹣2x.
【考点】二次函数图象与几何变换
【解析】【分析】(1)把(2,1)代入y=x2﹣2x+c中求出c的值即可得到抛物线解析式; (2)先确定抛物线y=x2﹣2x+1的对称轴,再利用抛物线的对称性得到A(0,0),B(2,0),然后利用交点式可写出新抛物线的表达式.
24.【答案】解:(1)∵点B(8,0)在抛物线y=-
1
4
x2+bx+4上, ∴-
1
4
×64+8b+4=0, 解得:b=
3
2
, ∴抛物线的解析式为:y=-
1
4
x2+
3
2
x+4, 对称轴为直线:x=-
3
2
2×
?
1
4
=3; (2)△AOC∽△COB. 理由如下:令y=0,则-
1
4
x2+
3
2
x+4=0, 即x2-6x-16=0, 解得x1=-2,x2=8, ∴点A的坐标为(-2,0), 令x=0,则y=4, ∴点C的坐标为(0,4), ∴OA=2,OB=8,OC=4, ∵
????
????
=
????
????
=2,∠AOC=∠COB=90°, ∴△AOC∽△COB; (3)设直线BC的解析式为y=kx+b, 则
8??+??=0
??=4
, 解得
??=?
1
2
??=4
, ∴直线BC的解析式为y=-
1
2
x+4, ∵MN∥y轴, ∴MN=-
1
4
x2+
3
2
x+4-(-
1
2
x+4), =-
1
4
x2+
3
2
x+4+
1
2
x-4, =-
1
4
x2+2x, =-
1
4
(x-4)2+4, ∴当x=4时,MN的值最大,最大值为4; (4)由勾股定理得,AC=
2
2
+
4
2
=2
5
, 过点C作CD⊥对称轴于D,则CD=3, ①AC=CQ时,DQ=
??
??
2
???
??
2
=
2
5
2
?
3
2
=
11
, 点Q在点D的上方时,点Q到x轴的距离为4+
11
, 此时点Q1(3,4+
11
), 点Q在点D的下方时,点Q到x轴的距离为4-
11
, 此时点Q2(3,4-
11
), ②点Q为对称轴与x轴的交点时,AQ=5, CQ=
3
2
+
4
2
=5, ∴AQ=CQ, 此时,点Q3(3,0), 综上所述,点Q的坐标为(3,4+
11
)或(3,4-
11
)或(3,0)时,△ACQ为等腰三角形时.
【考点】待定系数法求一次函数解析式,二次函数的最值,待定系数法求二次函数解析式,抛物线与x轴的交点,等腰三角形的性质,相似三角形的判定,与二次函数有关的动态几何问题
【解析】【分析】(1)把点B的坐标代入抛物线解析式求出b的值,即可得到抛物线解析式,再根据对称轴方程列式计算即可得解; (2)令y=0,解方程求出点A的坐标,令x=0求出y的值得到点C的坐标,再求出OA、OB、OC,然后根据对应边成比例,夹角相等的两个三角形相似证明; (3)设直线BC的解析式为y=kx+b,利用待定系数法求出解析式,再表示出MN,然后根据二次函数的最值问题解答; (4)利用勾股定理列式求出AC,过点C作CD⊥对称轴于D,然后分①AC=CQ时,利用勾股定理列式求出DQ,分点Q在点D的上方和下方两种情况求出点Q到x轴的距离,再写出点的坐标即可;②点Q为对称轴与x轴的交点时,AQ=CQ,再写出点Q的坐标即可.
25.【答案】解:(1)把A(3,4)代入y=x+m 得m=1, ∴ y=x+1, ∴B(0,1), 设二次函数解析式为y=ax2+bx+c, 把A.B.C三点坐标代入得
9??+3??+??=4
??=1
??+??+??=0
解得
??=1
??=?2
??=1
∴y=x2-2x+1; (2)∵P点在直线y=x+1的图象上, ∴P点坐标为(x,x+1), ∵E点在抛物线y=x2-2x+1的图象上, ∴E点坐标为(x,x2-2x+1), ∴h=(x+1)-(x2-2x+1)=-x2+3x; (3)存在. 易求D点坐标为(1,2),则DC=2, 当PE=2时,PE∥DC,四边形DCEP为平行四边形, 即 -x2+3x=2解得x1=1,x2=2, 当x=1时,PE与DC重合, 当x=2时,代入y=x+1,y=3 ∴ P点坐标为(2,3).
【考点】二次函数与一次函数的交点问题
【解析】【分析】 (1)因为直线y=x+m过点A,将A点坐标直接代入解析式即可求得m的值;设出二次函数的顶点式,将(3,4)代入即可; (2)由于P和E的横坐标相同,将P点横坐标代入直线和抛物线解析式,可得其纵坐标表达式; (3)先假设存在点P,根据四边形DCEP是平行四形的条件进行推理,若能求出P点坐标,则证明存在点P,否则P点不存在.
26.【答案】(1)将B、C两点的坐标代入得 /, 解得:b=?2,c=?3; 所以二次函数的表达式为:y=x2-2x-3 (2)存在点P,使四边形POP′C为菱形; 设P点坐标为(x,x2-2x-3),PP′交CO于E 若四边形POP′C是菱形,则有PC=PO; 连接PP′,则PE⊥CO于E, / ∴OE=EC=/ ∴y=?/; ∴x2-2x-3=?/ 解得x1=/, x2=/(不合题意,舍去) ∴P点的坐标为(/, ?/) (3)过点P作y轴的平行线与BC交于点Q,与OB交于点F,设P(x,x2-2x-3), / 易得,直线BC的解析式为y=x-3 则Q点的坐标为(x,x-3); S四边形ABPC=S△ABC+S△BPQ+S△CPQ =/AB?OC+/QP?BF+/QP?OF =/×4×3+/(?x2+3x)×3 =?/(x?/)2+/ 当x=/时,四边形ABPC的面积最大 此时P点的坐标为(/, ?/),四边形ABPC的面积的最大值为/.
【考点】待定系数法求二次函数解析式
【解析】【分析】(1)将B、C的坐标代入抛物线的解析式中即可求得待定系数的值; (2)由于菱形的对角线互相垂直平分,若四边形POP′C为菱形,那么P点必在OC的垂直平分线上,据此可求出P点的纵坐标,代入抛物线的解析式中即可求出P点的坐标; (3) 由于△ABC的面积为定值,当四边形ABPC的面积最大时,△BPC的面积最大;过P作y轴的平行线,交直线BC于Q,交x轴于F,易求得直线BC的解析 式,可设出P点的横坐标,然后根据抛物线和直线BC的解析式求出Q、P的纵坐标,即可得到PQ的长,以PQ为底,B点横坐标的绝对值为高即可求得△BPC 的面积,由此可得到关于四边形ACPB的面积与P点横坐标的函数关系式,根据函数的性质即可求出四边形ABPC的最大面积及对应的P点坐标.
27.【答案】(1)解:由题意抛物线的顶点坐标为(2,﹣
8
3
),设抛物线的解析式为y=a(x﹣2)2﹣
8
3
,把(0,0)代入得到a=
2
3
, ∴抛物线的解析式为y=
2
3
(x﹣2)2﹣
8
3
,即y=
2
3
x2﹣
8
3
x (2)解:如图1中,设E(m,0),则C(m,
2
3
m2﹣
8
3
m),B(﹣
2
3
m2+
11
3
m,0),/ ∵E′在抛物线上, ∴E、B关于对称轴对称, ∴
??+(?
2
3
??
2
+
11
3
??)
2
=2, 解得m=1或6(舍弃), ∴B(3,0),C(1,﹣2), ∴直线l′的解析式为y=x﹣3 (3)解:如图2中,
/ ①当P1与N重合时,△P1B′N′是等腰三角形,此时P1(0,﹣3). ②当N′=N′B′时,设P(m,m﹣3), 则有(m﹣
3
2
2
)2+(m﹣3﹣
3
2
2
)2=(3
2
)2 , 解得m=
3
2
+3?3
3
2
或
3
2
+3+3
3
2
, ∴P2(
3
2
+3?3
3
2
,
3
2
?3?3
3
2
),P3(
3
2
+3+3
3
2
,
3
2
?3+3
3
2
). 综上所述,满足条件的点P坐标为(0,﹣3)或(
3
2
+3?3
3
2
,
3
2
?3?3
3
2
)或(
3
2
+3+3
3
2
,
3
2
?3+3
3
2
).
【考点】待定系数法求一次函数解析式,待定系数法求二次函数解析式,二次函数与一次函数的综合应用
【解析】【分析】(1)根据二次函数的顶点坐标设出顶点式,根据抛物线经过原点,将原点坐标代入即可求出解析式; (2)设E(m,0),然后用含m的式子表示出点B和点C的坐标,根据E′在抛物线上,可知E、B关于对称轴对称,进而根据点E和点B到对称轴的距离相等列式,求出m的值,得到点B和点C的坐标,即可求出直线l′ 的解析式; (3)分两种情况分析:①当P1与N重合时,△P1B′N′是等腰三角形;②当N′=N′B′时,设P(m,m﹣3),然后利用勾股定理求出m的值,即可得解.
28.【答案】(1)点M? (1)经过t秒时,/, /, 则/, / ∵/=/=/, ∴/??? ∴/?? ∴//? ∴/? ∵/∴当/时,S的值最大. (1)存在。 设经过t秒时,NB=t,OM="2t" ,则/, /∴/=/=/? ①若/, 则/是等腰Rt△/底边/上的高, ∴/是底边/的中线???? ∴/, ∴/, ∴/, ??????? ∴点/的坐标为(1,0) ②若/, 此时/与/重合,∴/, ∴/, ∴/????????? ∴点/的坐标为(2,0)
【考点】二次函数的最值,勾股定理
【解析】【分析】 (1)由于点M比点N先出发并且点M的速度比点N大,可知点M能到达终点. (2)经过t秒时可得NB=y,OM-2t.根据∠BCA=∠MAQ=45°推出QN=CN,PQ的值.求出S与t的函数关系式后根据t的值求出S的最大值. (3)本题分两种情况讨论(若∠AQM=90°,PQ是等腰Rt△MQA底边MA上的高; 若∠QMA=90°,QM与QP重合)求出t值.
一、单选题(共10题;共30分)
1.将抛物线y=-2x2+1向右平移1个单位,再向上平移2个单位后所得到的抛物线为(?? )
A.?y=-2(x+1)2-1?????????/B.?y=-2(x+1)2+3?????????/C.?y=-2(x-1)2+1?????????/D.?y=-2(x-1)2+3
2.已知关于x的函数y=(m﹣1)xm+(3m+2)x+1是二次函数,则此解析式的一次项系数是(?? )
A.?﹣1?????????????????????????????????????????/B.?8?????????????????????????????????????????/C.?﹣2?????????????????????????????????????????/D.?1
3.把抛物线y=-2x2先向右平移1个单位长度,再向上平移2个单位长度后,所得函数的表达式为( ??)
A.?y=-2(x+1)2+2??????????/B.?y=-2(x+1)2-2??????????/C.?y=-2(x-1)2+2??????????/D.?y=-2(x-1)2-2
4.如图所示是一个抛物线形桥拱的示意图,在所给出的平面直角坐标系中,当水位在AB位置时,水面宽度为10m,此时水面到桥拱的距离是4m,则抛物线的函数关系式为(??? )
/
A.?y=
25
4
??
2
?????????????????????????/B.?y=﹣
25
4
??
2
?????????????????????????/C.?y=﹣
4
25
??
2
?????????????????????????/D.?y=
4
25
??
2
5.已知二次函数y=ax2+bx+c的图象如图所示,则下列结论中:①ac>0;②a+b+c<0;③4a﹣2b+c<0;④2a+b<0;⑤4ac﹣b2<4a;⑥a+b>0中,其中正确的个数为(?? )
/
A.?2???????????????????????????????????????????/B.?3???????????????????????????????????????????/C.?4???????????????????????????????????????????/D.?5
6.已知二次函数 ??=
??
2
+??+?? ,当 ?? 取任意实数时,都有 ??>0 ,则 ?? 的取值范围是(??? ).
A.??≥
1
4
B.??>
1
4
C.??≤
1
4
D.??<
1
4
7.下列关系式中,属于二次函数的是(x是自变量)( )
A.?y=
1
3
??
2
???????????????????????????/B.?y=
??
2
?1
???????????????????????????/C.?y=
1
??
2
???????????????????????????/D.?y=ax2+bx+c
8.已知二次函数 ??=??
??
2
+????+??(??≠0) 的图象如图所示,有下列4个结论,其中正确的结论是( ??) /
A.???????>0?????????????????????????B.?2?????=0?????????????????????????C.???>??+???????????????????????????D.?
??
2
?4????<0 ?
9.若A(-4,y1),B(-3,y2),C(1,y3)为二次函数y=x2+4x-m的图象上的三点,则y1 , y2 , y3的大小关系是(?? )
A.y1<y2<y3 B.y2<y1<y3 C.y3 <y1<y2 D.y1<y3<y2
10.抛物线y=ax2+bx+c的图角如图,则下列结论:①abc>0;②a+b+c=2;③a<
1
2
;④b>1.其中正确的结论是( ) /
A.?①②?????????????????????????????????????B.?②③?????????????????????????????????????C.?②④?????????????????????????????????????D.?③④
二、填空题(共10题;共30分)
11.把抛物线 ??=
(???1)
2
+2 沿x轴向左平移4个单位,再沿y轴向上平移3个单位后,所得新抛物线相应的函数表达式是________.
12.若抛物线y=x2-2x-3与x轴分别交于A,B两点,则AB的长为 ________.
13.如果抛物线y=2x2与抛物线y=ax2关于x轴对称,那么a的值是________.
14.若二次函数y=ax2+bx+c(a≠0)的图象与x轴有两个交点,坐标分别为(x1 , 0)、(x2 , 0),且x1<x2 , 图象上有一点M(x0 , y0)在x轴下方,在下列四个算式中判定正确的是________ ?①a(x0﹣x1)(x0﹣x2)<0;②a>0;③b2﹣4ac≥0;④x1<x0<x2 .
15.抛物线y=x2﹣6x+5向上平移2个单位长度,再向右平移1个单位长度后,得到的抛物线解析式是________?.
16.如图,边长为1的正方形ABCO,以A为顶点,且经过点C的抛物线与对角线交于点D,点D的坐标为________. /
17.如图,二次函数y=x2﹣6x+5的图象交x轴于A、B两点,交y轴于点C,则△ABC的面积为________?. ?/
18.将抛物线 ??=2
(???1)
2
+4 ,绕着它的顶点旋转
180
°
,旋转后的抛物线表达式是________.
19.将抛物??=?
???1
2
向左平移1个单位后,得到的抛物线的解析式是________.
20.如图,边长为1的正方形ABCD的对角线AC,BD相交于点O,直角∠MPN的顶点P与点O重合,直角边PM,PN分别与OA,OB重合,然后逆时针旋转∠MPN,旋转角为θ(0°<θ<90°),PM、PN分别交AB、BC于E、F两点,连接EF交OB于点G,则下列结论中正确的是________. ①EF=
2
OE;②S四边形OEBF:S正方形ABCD=1:4;③在旋转过程中,当△BEF与△COF的面积之和最大时,AE=
3
4
;④OG?BD=AE2+CF2 . /
三、解答题(共8题;共60分)
21.已知如图,抛物线的顶点D的坐标为(1,-4),且与y轴交于点C(0,3).(1)求该函数的关系式;(2)求该抛物线与x轴的交点A,B的坐标. /
22.如图,人工喷泉有一个竖直的喷水枪AB,喷水口A距地面2m,喷出水流的运动路线是抛物线. 如果水流的最高点P到喷水枪AB所在直线的距离为1m,且到地面的距离为3.6m,求水流的落地点C到水枪底部B的距离. /
23.抛物线y=x2﹣2x+c经过点(2,1). (1)求抛物线的顶点坐标; (2)将抛物线y=x2﹣2x+c沿y轴向下平移后,所得新抛物线与x轴交于A、B两点,如果AB=2,求新抛物线的表达式.
24.如图,已知抛物线y=-
1
4
??
2
+bx+4与x轴相交于A、B两点,与y轴相交于点C,若已知B点的坐标为B(8,0). / (1)求抛物线的解析式及其对称轴方程; (2)连接AC、BC,试判断△AOC与△COB是否相似?并说明理由; (3)M为抛物线上BC之间的一点,N为线段BC上的一点,若MN∥y轴,求MN的最大值; (4)在抛物线的对称轴上是否存在点Q,使△ACQ为等腰三角形?若存在,求出符合条件的Q点坐标;若不存在,请说明理由.
25.已知二次函数图象顶点为C(1,0),直线y=x+m与该二次函数交于A,B两点,其中A点(3,4),B点在y轴上. / (1)求此二次函数的解析式; (2)P为线段AB上一动点(不与A,B重合),过点P作y轴的平行线与二次函数交于点E.设线段PE长为h,点P横坐标为x,求h与x之间的函数关系式; (3)D为线段AB与二次函数对称轴的交点,在AB上是否存在一点P,使四边形DCEP为平行四边形?若存在,请求出P点坐标;若不存在,请说明理由.
26.如图,在平面直角坐标系中,二次函数y=x2+bx+c的图象与x轴交于A、B两点,A点在原点的左侧,B点的坐标为(3,0),与y轴交于C(0,﹣3)点,点P是直线BC下方的抛物线上一动点. / (1)求这个二次函数的表达式. (2)连接PO、PC,并把△POC沿CO翻折,得到四边形POP′C,那么是否存在点P,使四边形POP′C为菱形?若存在,请求出此时点P的坐标;若不存在,请说明理由. (3)当点P运动到什么位置时,四边形ABPC的面积最大?求出此时P点的坐标和四边形ABPC的最大面积.
27.如图1,已知二次函数y=ax2+bx+c(a、b、c为常数,a≠0)的图象过点O(0,0)和点A(4,0),函数图象最低点M的纵坐标为﹣
8
3
,直线l的解析式为y=x.
/
(1)求二次函数的解析式;
(2)直线l沿x轴向右平移,得直线l′,l′与线段OA相交于点B,与x轴下方的抛物线相交于点C,过点C作CE⊥x轴于点E,把△BCE沿直线l′折叠,当点E恰好落在抛物线上点E′时(图2),求直线l′的解析式;
(3)在(2)的条件下,l′与y轴交于点N,把△BON绕点O逆时针旋转135°得到△B′ON′,P为l′上的动点,当△PB′N′为等腰三角形时,求符合条件的点P的坐标.
28.如图, 四边形OABC为直角梯形,A(4,0),B(3,4),C(0,4). 点M从O 出发以每秒2个单位长度的速度向A运动;点N从B同时出发,以每秒1个单位长度的速度向C运动.其中一个动点到达终点时,另一个动点也随之停止运动.过点N作NP垂直/轴于点P,连结AC交NP于Q,连结MQ. / (1)点?????(填M或N)能到达终点; (2)求△AQM的面积S与运动时间t的函数关系式,并写出自变量t的取值范围,当t为何值时,S的值最大; (3)是否存在点M,使得△AQM为直角三角形?若存在,求出点M的坐标,若不存在, 说明理由.//
答案解析部分
一、单选题
1.【答案】D
【考点】二次函数图象的几何变换
【解析】【解答】根据左加右减,上加下减的归则.将抛物线y=-2x2+1向右平移1个单位得y=-2(x-1)2+3,再向上平移2个单位得y=-2(x-1)2+3.故答案为:D.
【分析】根据平移规律“左加右减,上加下减“”即可求解。
2.【答案】B
【考点】二次函数的定义
【解析】【解答】解:∵关于x的函数y=(m﹣1)xm+(3m+2)x+1是二次函数,∴m=2, 则3m+2=8, 故此解析式的一次项系数是:8. 故答案为:B 【分析】根据二次函数的定义,自变量的最高次数是2,得出m的值,再将m的值代入3m+2即可算出一次项的系数。
3.【答案】C
【考点】二次函数图象的几何变换
【解析】【解答】解:把抛物线y=-2x2先向右平移1个单位长度,再向上平移2个单位长度后,所得函数的表达式为y=-2(x-1)2+2,故答案为:C. 【分析】根据函数平移的特点“上加下减,左加右减”,向右平移一个单位,x减去1,向上平移2个单位,函数解析式末尾加上2。
4.【答案】C
【考点】待定系数法求二次函数解析式
【解析】【解答】如图,由题意可设抛物线的解析式为 ??=??
??
2
,∵由题意可知点A、B的坐标分别为(-5,-4)、(5,-4),且抛物线过点A、B, ∴ 25??=?4 ,解得: ??=?
4
25
, ∴抛物线的解析式为:y=?
4
25
x2 故答案为:C. 【分析】先设抛物线为 y=ax2 , 根据题意可得出A、B的坐标分别为 (-5,-4)、(5,-4),将A、B的坐标代入 y=ax2 , 解出a,即为所求解析式。
5.【答案】C
【考点】二次函数图象与系数的关系
【解析】【解答】解:解:①图象开口向下,与y轴交于负半轴,对称轴在y轴右侧,能得到:a<0,c<0, ∴ac>0,故①正确;②当x=1时,y>0,∴a+b+c>0,故②错误;③当x=﹣2时,y<0,∴4a﹣2b+c<0,故③正确;④∵对称轴x=﹣
??
2??
<1, ∴2a+b>0,故④错误;⑤∵抛物线的顶点在x轴的上方, ∴
4?????
??
2
4??
>0, ∴4ac﹣b2<4a,故⑤正确;⑥∵2a+b>0, ∴2a+b﹣a>﹣a, ∴a+b>﹣a, ∵a<0, ∴﹣a>0, ∴a+b>0,故⑥正确; 综上所述正确的个数为4个, 故选:C. / 【分析】由抛物线的开口方向判断a与0的关系,由抛物线与y轴的交点判断c与0的关系,然后根据对称轴及抛物线的顶点坐标情况进行推理,进而对所得结论进行判断.
6.【答案】B
【考点】二次函数图象与系数的关系
【解析】【解答】已知二次函数的解析式为:y=x2+x+m,
∴函数的图象开口向上,
又∵当x取任意实数时,都有y>0,
∴有△<0,
∴△=1-4m<0,
∴m>
1
4
,
故答案为:B.
【分析】二次函数图像开口向上,故y>0即为函数与x轴无交点,那么只需所对应的一元二次方程没有实数根.
7.【答案】A
【考点】二次函数的定义
【解析】【解答】解:A、是二次函数,故A正确; B、不是二次函数的形式,故B错误; C、是分式,故C错误; D、a=0是一次函数,故D错误; 故选:A. 【分析】根据函数y=ax2+bx+c (a≠0)是二次函数,可得答案.
8.【答案】C
【考点】二次函数的图象,二次函数的性质,二次函数图象与系数的关系,抛物线与x轴的交点,二次函数图象上点的坐标特征
【解析】【解答】抛物线的开口向下,则a<0;…① 抛物线的对称轴为x=1,则-
??
2??
=1,b=-2a;…② 抛物线交y轴于正半轴,则c>0;…③ 抛物线与x轴有两个不同的交点,则:△=b2-4ac>0; 由②知:b>0,b+2a=0; 又由①③得:abc<0; 由图知:当x=-1时,y<0;即a-b+c<0,b>a+c; 故答案为:C. 【分析】根据抛物线的开口方向,对称轴的位置及抛物线与y轴的交点情况,可知a<0、c>0、b>0,即可对A作出判断;根据对称轴x=1,可得出b+2a=0,可对B作出判断;将b > a + c变形为a-b+c<0,根据x=-1,即可作出判断;根据抛物线与x轴的交点个数可对D作出判断。
9.【答案】B
【考点】二次函数y=ax^2+bx+c的性质
【解析】【解答】根据二次函数的解析式可知其对称轴为x= ?
??
2??
=-2,然后根据二次函数的图像可知开口向上,因此根据二次函数的增减性,可知y2<y1<y3.
故答案为:B
【分析】先求出抛物线的对称轴,再根据二次函数的图像可知开口向上,然后利用二次函数的增减性,可得出答案。
10.【答案】C
【考点】二次函数图象与系数的关系
【解析】
【分析】由抛物线的开口方向判断a与0的关系,由抛物线与y轴的交点判断c与0的关系,然后根据对称轴及抛物线与x轴交点情况进行推理,进而对所得结论进行判断.
【解答】①∵抛物线的开口向上,∴a>0, ∵与y轴的交点为在y轴的负半轴上,∴c<0, ∵对称轴为x=-
??
2??
<0,∴a、b同号,即b>0, ∴abc<0, 故本选项错误; ②当x=1时,函数值为2, ∴a+b+c=2; 故本选项正确; ③∵对称轴x=-
??
2??
>-1, 解得:
??
2
<a, ∵b>1, ∴a>
1
2
, 故本选项错误; ④当x=-1时,函数值<0, 即a-b+c<0,(1) 又a+b+c=2, 将a+c=2-b代入(1), 2-2b<0, ∴b>1 故本选项正确; 综上所述,其中正确的结论是②④; 故选C.
【点评】二次函数y=ax2+bx+c系数符号的确定: (1)a由抛物线开口方向确定:开口方向向上,则a>0;否则a<0. (2)b由对称轴和a的符号确定:由对称轴公式x=-
??
2??
判断符号. (3)c由抛物线与y轴的交点确定:交点在y轴正半轴,则c>0;否则c<0. (4)b2-4ac的符号由抛物线与x轴交点的个数确定:2个交点,b2-4ac>0;1个交点,b2-4ac=0;没有交点,b2-4ac<0. (5)当x=1时,可确定a+b+c的符号,当x=-1时,可确定a-b+c的符号. (6)由对称轴公式x=-
??
2??
, 可确定2a+b的符号
二、填空题
11.【答案】/
【考点】二次函数图象的几何变换
【解析】【解答】把抛物线 ??=
(???1)
2
+2 沿x轴向左平移4个单位得 ??=
(??+3)
2
+2 ,再沿y轴向上平移3个单位后得 ??=
(??+3)
2
+5 .
故答案为: ??=
(??+3)
2
+5 .
【分析】根据抛物线的几何变换规律,在顶点式的完全平方式内左加右减,在顶点式的常数项处上加下减,即可得出平移后新函数的函数解析式。
12.【答案】4
【考点】二次函数图像与坐标轴的交点问题
【解析】【解答】二次函数y=x2-2x-3与x轴交点A、B的横坐标为一元二次方程x2-2x-3=0的两个根,求得x1=-1,x2=3,则AB=|x2-x1|=4.【分析】先令y=0求出二次函数与x轴的交点A、B,两个交点的横坐标x1、x2 之间的距离即为AB的长。
13.【答案】-2
【考点】二次函数y=ax^2的图像
【解析】【解答】根据关于x轴对称的抛物线的开口方向改变,开口大小不变,可由抛物线y=2x2与抛物线y=ax2关于x轴对称,知两抛物线开口大小不变,方向相反,因此可得a=﹣2. 故答案为:﹣2. 【分析】根据关于x轴对称的抛物线的开口方向改变,开口程度不变可得a=﹣2。
14.【答案】①
【考点】二次函数图象与系数的关系,抛物线与x轴的交点
【解析】【解答】解: ∵二次函数y=ax2+bx+c(a≠0)的图象与x轴有两个交点无法确定a的正负情况, ∴选项②项错误; ∵二次函数y=ax2+bx+c(a≠0)的图象与x轴有两个交点,且坐标分别为(x1 , 0)、(x2 , 0),且x1<x2 , ∴b2﹣4ac>0,故选项③错误; 若a>0,则x1<x0<x2 , 若a<0,则x0<x1<x2或x1<x2<x0 , 故选项④错误 若a>0,则x0﹣x1>0,x0﹣x2<0, ∴(x0﹣x1)(x0﹣x2)<0, ∴a(x0﹣x1)(x0﹣x2)<0, 若a<0,则(x0﹣x1)与(x0﹣x2)同号, ∴a(x0﹣x1)(x0﹣x2)<0, 综上所述,a(x0﹣x1)(x0﹣x2)<0正确,故选项①正确, 故答案为:①. 【分析】根据抛物线与x轴有两个不同的交点,根的判别式△>0,再分a>0和a<0两种情况对各选项讨论即可得解.
15.【答案】y=(x﹣4)2﹣3
【考点】二次函数图象的几何变换
【解析】【解答】解:y=x2﹣6x+5=(x﹣3)2﹣4,其顶点坐标为(3,﹣4). 向上平移2个单位长度,再向右平移1个单位长度后的顶点坐标为(4,﹣3),得到的抛物线的解析式是y=(x﹣4)2﹣2, 故答案为:y=(x﹣4)2﹣2. 【分析】根据题意易得新抛物线的顶点,根据顶点式及平移前后二次项的系数不变可得新抛物线的解析式.
16.【答案】(
3?
5
2
,
3?
5
2
)
【考点】待定系数法求二次函数解析式,二次函数的应用,正方形的性质,二次函数与一次函数的综合应用
【解析】【解答】解:A的坐标是(1,0)、C坐标是(0,1),设出解析式是y=a(x﹣1)2 , 把C的坐标代入得:a(﹣1)2=1, 解得:a=1, 则抛物线的解析式是:y=(x﹣1)2; ∵B的坐标是(1,1), 设OB解析式的解析式是y=kx,则k=1,则OB的解析式是y=x. 根据题意得: {
??=
(???1)
2
??=??
, 解得: {
??=
3+
5
2
??=
3+
5
2
(舍去),或 {
??=
3?
5
2
??=
3?
5
2
. 则D的坐标是:(
3?
5
2
,
3?
5
2
). 故答案为:(
3?
5
2
,
3?
5
2
). 【分析】根据图形首先求得A、B、C的坐标,利用待定系数法即可求得抛物线的解析式和直线OB的解析式,然后两函数解析式联立组成的方程组即可求解。
17.【答案】10
【考点】二次函数图像与坐标轴的交点问题
【解析】【解答】解:在y=x2﹣6x+5中, 当y=0时,x=1或5; 当x=0时,y=5; 则A(1,0)、B(5,0)、C(0,5) 故△ABC的面积为:
1
2
×4×5=10; 故答案为:10. ?/ 【分析】根据解析式求出A、B、C三点的坐标,即△ABC的底和高求出,然后根据三角形的面积公式进行计算即可.
18.【答案】??=?2
(???1)
2
+4
【考点】二次函数图象的几何变换
【解析】【解答】解:抛物线 ??=2
(???1)
2
+4 的顶点为(1,4),
∵原抛物线是绕顶点(1,4)旋转,
∴旋转后的抛物线的顶点依然是(1,4).
∵旋转了180°,
∴原来开口向上变成开口向下,但开口形状不变,∴二次项系数为-2,
∴旋转后的抛物线表达式为 ??=?2
(???1)
2
+4 ,
故答案为: ??=?2
(???1)
2
+4
【分析】求抛物线的几何变化中的解析式,需要将解析式化成顶点式;根据顶点变化,及二次项系数的变化,可得到新的解析式.以顶点为中心旋转,∴顶点不变,但抛物线的开口方向变了.
19.【答案】??=
??
2
【考点】二次函数图象与几何变换
【解析】【解答】 ∵向左平移1个单位∴y=-(x-1+1)2=-x2 . 故得到的抛物线的解析式是y=-x2 . 【分析】根据二次函数图象的平移规律“上加下减,左加右减”进行解题.
20.【答案】①②④
【考点】二次函数的最值,全等三角形的判定与性质,相似三角形的判定与性质
【解析】【解答】解:①∵四边形ABCD是正方形, ∴OB=OC,∠OBE=∠OCF=45°,∠BOC=90°, ∴∠BOF+∠COF=90°, ∵∠EOF=90°, ∴∠BOF+∠COE=90°, ∴∠BOE=∠COF, 在△BOE和△COF中, {
∠??????=∠??????
????=????
∠??????=∠??????
, ∴△BOE≌△COF(ASA), ∴OE=OF,BE=CF, ∴EF=
2
OE;故正确; ②∵S四边形OEBF=S△BOE+S△BOE=S△BOE+S△COF=S△BOC=
1
4
S正方形ABCD , ∴S四边形OEBF:S正方形ABCD=1:4;故正确; ③过点O作OH⊥BC, / ∵BC=1, ∴OH=
1
2
BC=
1
2
, 设AE=x,则BE=CF=1﹣x,BF=x, ∴S△BEF+S△COF=
1
2
BE?BF+
1
2
CF?OH=
1
2
x(1﹣x)+
1
2
(1﹣x)×
1
2
=﹣
1
2
(x﹣
1
4
)2+
9
32
, ∵a=﹣
1
2
<0, ∴当x=
1
4
时,S△BEF+S△COF最大; 即在旋转过程中,当△BEF与△COF的面积之和最大时,AE=
1
4
;故错误; ④∵∠EOG=∠BOE,∠OEG=∠OBE=45°, ∴△OEG∽△OBE, ∴OE:OB=OG:OE, ∴OG?OB=OE2 , ∵OB=
1
2
BD,OE=
2
2
EF, ∴OG?BD=EF2 , ∵在△BEF中,EF2=BE2+BF2 , ∴EF2=AE2+CF2 , ∴OG?BD=AE2+CF2 . 故正确. 故答案为:①②④. 【分析】①根据全等三角形的定义,通过ASA判定得出△BOE≌△COF, 以此得出结论。 ②求证S四边形OEBF=S△BOC=
1
4
S正方形ABCD,得出结论。 ③设AE=x,则BE=CF=1﹣x,BF=x,表示出S△BEF+S△COF,求出S△BEF+S△COF最大时的x值。 ④证出△OEG∽△OBE,由相似三角形的对应边成比例,求证出OG?BD=AE2+CF2。
三、解答题
21.【答案】解:(1)∵抛物线的顶点D的坐标为(1,?4), ∴设抛物线的函数关系式为y=a(x?1)2?4, 又∵抛物线过点C(0,3), ∴3=a(0?1)2?4, 解得a=1, ∴抛物线的函数关系式为y=(x?1)2?4, 即y=x2?2x?3; ( 2 )令y=0,得:x2 ?2???3=0 , 解得
??
1
=3 ,
??
2
=?1 . 所以坐标为A(3,0),B(-1,0).
【考点】待定系数法求二次函数解析式,二次函数图像与坐标轴的交点问题
【解析】【分析】(1)设出抛物线方程的顶点式,将点C的坐标代入即可求得抛物线方程;(2)对该抛物线令y=0,解二元一次方程即可求得点A,B的坐标.
22.【答案】解:建立平面直角坐标系,如图, / 于是抛物线的表达式可以设为 ??=??
(????)
2
+?? ?, 根据题意,得出A,P两点的坐标分别为A(0,2),P(1,3.6), ∵点P为抛物线顶点, ∴ ?=1,??=3.6 ?, ∵点A在抛物线上, ∴ ??+3.6=2 , ??=?1.6 , ∴它的表达式为 ??=?1.6
(???1)
2
+3.6 , 当点C的纵坐标y=0时,有 ?1.6
(???1)
2
+3.6=0 ,
??
1
=?0.5 (舍去),
??
2
=2.5 , ∴BC=2.5, ∴水流的落地点C到水枪底部B的距离为2.5m
【考点】二次函数的图象,待定系数法求二次函数解析式,抛物线与x轴的交点,二次函数的应用
【解析】【分析】将实际问题转化为数学问题,根据喷水口A距地面2m,可得出点A的坐标为(0,2),根据水流的最高点P到喷水枪AB所在直线的距离为1m,且到地面的距离为3.6m,得出抛物线的顶点P的坐标为(1,3.6),因此设函数解析式为顶点式,再将点A的坐标代入即可求出函数解析式,然后由y=0建立方程求出x的值,根据实际情况取值即可。
23.【答案】解:(1)把(2,1)代入y=x2﹣2x+c得4﹣4+c=1,解得c=1, 所以抛物线解析式为y=x2﹣2x+1; (2)y=x2﹣2x+1=(x﹣1)2 , 抛物线的对称轴为直线x=1, 而新抛物线与x轴交于A、B两点,AB=2, 所以A(0,0),B(2,0), 所以新抛物线的解析式为y=x(x﹣2),即y=x2﹣2x.
【考点】二次函数图象与几何变换
【解析】【分析】(1)把(2,1)代入y=x2﹣2x+c中求出c的值即可得到抛物线解析式; (2)先确定抛物线y=x2﹣2x+1的对称轴,再利用抛物线的对称性得到A(0,0),B(2,0),然后利用交点式可写出新抛物线的表达式.
24.【答案】解:(1)∵点B(8,0)在抛物线y=-
1
4
x2+bx+4上, ∴-
1
4
×64+8b+4=0, 解得:b=
3
2
, ∴抛物线的解析式为:y=-
1
4
x2+
3
2
x+4, 对称轴为直线:x=-
3
2
2×
?
1
4
=3; (2)△AOC∽△COB. 理由如下:令y=0,则-
1
4
x2+
3
2
x+4=0, 即x2-6x-16=0, 解得x1=-2,x2=8, ∴点A的坐标为(-2,0), 令x=0,则y=4, ∴点C的坐标为(0,4), ∴OA=2,OB=8,OC=4, ∵
????
????
=
????
????
=2,∠AOC=∠COB=90°, ∴△AOC∽△COB; (3)设直线BC的解析式为y=kx+b, 则
8??+??=0
??=4
, 解得
??=?
1
2
??=4
, ∴直线BC的解析式为y=-
1
2
x+4, ∵MN∥y轴, ∴MN=-
1
4
x2+
3
2
x+4-(-
1
2
x+4), =-
1
4
x2+
3
2
x+4+
1
2
x-4, =-
1
4
x2+2x, =-
1
4
(x-4)2+4, ∴当x=4时,MN的值最大,最大值为4; (4)由勾股定理得,AC=
2
2
+
4
2
=2
5
, 过点C作CD⊥对称轴于D,则CD=3, ①AC=CQ时,DQ=
??
??
2
???
??
2
=
2
5
2
?
3
2
=
11
, 点Q在点D的上方时,点Q到x轴的距离为4+
11
, 此时点Q1(3,4+
11
), 点Q在点D的下方时,点Q到x轴的距离为4-
11
, 此时点Q2(3,4-
11
), ②点Q为对称轴与x轴的交点时,AQ=5, CQ=
3
2
+
4
2
=5, ∴AQ=CQ, 此时,点Q3(3,0), 综上所述,点Q的坐标为(3,4+
11
)或(3,4-
11
)或(3,0)时,△ACQ为等腰三角形时.
【考点】待定系数法求一次函数解析式,二次函数的最值,待定系数法求二次函数解析式,抛物线与x轴的交点,等腰三角形的性质,相似三角形的判定,与二次函数有关的动态几何问题
【解析】【分析】(1)把点B的坐标代入抛物线解析式求出b的值,即可得到抛物线解析式,再根据对称轴方程列式计算即可得解; (2)令y=0,解方程求出点A的坐标,令x=0求出y的值得到点C的坐标,再求出OA、OB、OC,然后根据对应边成比例,夹角相等的两个三角形相似证明; (3)设直线BC的解析式为y=kx+b,利用待定系数法求出解析式,再表示出MN,然后根据二次函数的最值问题解答; (4)利用勾股定理列式求出AC,过点C作CD⊥对称轴于D,然后分①AC=CQ时,利用勾股定理列式求出DQ,分点Q在点D的上方和下方两种情况求出点Q到x轴的距离,再写出点的坐标即可;②点Q为对称轴与x轴的交点时,AQ=CQ,再写出点Q的坐标即可.
25.【答案】解:(1)把A(3,4)代入y=x+m 得m=1, ∴ y=x+1, ∴B(0,1), 设二次函数解析式为y=ax2+bx+c, 把A.B.C三点坐标代入得
9??+3??+??=4
??=1
??+??+??=0
解得
??=1
??=?2
??=1
∴y=x2-2x+1; (2)∵P点在直线y=x+1的图象上, ∴P点坐标为(x,x+1), ∵E点在抛物线y=x2-2x+1的图象上, ∴E点坐标为(x,x2-2x+1), ∴h=(x+1)-(x2-2x+1)=-x2+3x; (3)存在. 易求D点坐标为(1,2),则DC=2, 当PE=2时,PE∥DC,四边形DCEP为平行四边形, 即 -x2+3x=2解得x1=1,x2=2, 当x=1时,PE与DC重合, 当x=2时,代入y=x+1,y=3 ∴ P点坐标为(2,3).
【考点】二次函数与一次函数的交点问题
【解析】【分析】 (1)因为直线y=x+m过点A,将A点坐标直接代入解析式即可求得m的值;设出二次函数的顶点式,将(3,4)代入即可; (2)由于P和E的横坐标相同,将P点横坐标代入直线和抛物线解析式,可得其纵坐标表达式; (3)先假设存在点P,根据四边形DCEP是平行四形的条件进行推理,若能求出P点坐标,则证明存在点P,否则P点不存在.
26.【答案】(1)将B、C两点的坐标代入得 /, 解得:b=?2,c=?3; 所以二次函数的表达式为:y=x2-2x-3 (2)存在点P,使四边形POP′C为菱形; 设P点坐标为(x,x2-2x-3),PP′交CO于E 若四边形POP′C是菱形,则有PC=PO; 连接PP′,则PE⊥CO于E, / ∴OE=EC=/ ∴y=?/; ∴x2-2x-3=?/ 解得x1=/, x2=/(不合题意,舍去) ∴P点的坐标为(/, ?/) (3)过点P作y轴的平行线与BC交于点Q,与OB交于点F,设P(x,x2-2x-3), / 易得,直线BC的解析式为y=x-3 则Q点的坐标为(x,x-3); S四边形ABPC=S△ABC+S△BPQ+S△CPQ =/AB?OC+/QP?BF+/QP?OF =/×4×3+/(?x2+3x)×3 =?/(x?/)2+/ 当x=/时,四边形ABPC的面积最大 此时P点的坐标为(/, ?/),四边形ABPC的面积的最大值为/.
【考点】待定系数法求二次函数解析式
【解析】【分析】(1)将B、C的坐标代入抛物线的解析式中即可求得待定系数的值; (2)由于菱形的对角线互相垂直平分,若四边形POP′C为菱形,那么P点必在OC的垂直平分线上,据此可求出P点的纵坐标,代入抛物线的解析式中即可求出P点的坐标; (3) 由于△ABC的面积为定值,当四边形ABPC的面积最大时,△BPC的面积最大;过P作y轴的平行线,交直线BC于Q,交x轴于F,易求得直线BC的解析 式,可设出P点的横坐标,然后根据抛物线和直线BC的解析式求出Q、P的纵坐标,即可得到PQ的长,以PQ为底,B点横坐标的绝对值为高即可求得△BPC 的面积,由此可得到关于四边形ACPB的面积与P点横坐标的函数关系式,根据函数的性质即可求出四边形ABPC的最大面积及对应的P点坐标.
27.【答案】(1)解:由题意抛物线的顶点坐标为(2,﹣
8
3
),设抛物线的解析式为y=a(x﹣2)2﹣
8
3
,把(0,0)代入得到a=
2
3
, ∴抛物线的解析式为y=
2
3
(x﹣2)2﹣
8
3
,即y=
2
3
x2﹣
8
3
x (2)解:如图1中,设E(m,0),则C(m,
2
3
m2﹣
8
3
m),B(﹣
2
3
m2+
11
3
m,0),/ ∵E′在抛物线上, ∴E、B关于对称轴对称, ∴
??+(?
2
3
??
2
+
11
3
??)
2
=2, 解得m=1或6(舍弃), ∴B(3,0),C(1,﹣2), ∴直线l′的解析式为y=x﹣3 (3)解:如图2中,
/ ①当P1与N重合时,△P1B′N′是等腰三角形,此时P1(0,﹣3). ②当N′=N′B′时,设P(m,m﹣3), 则有(m﹣
3
2
2
)2+(m﹣3﹣
3
2
2
)2=(3
2
)2 , 解得m=
3
2
+3?3
3
2
或
3
2
+3+3
3
2
, ∴P2(
3
2
+3?3
3
2
,
3
2
?3?3
3
2
),P3(
3
2
+3+3
3
2
,
3
2
?3+3
3
2
). 综上所述,满足条件的点P坐标为(0,﹣3)或(
3
2
+3?3
3
2
,
3
2
?3?3
3
2
)或(
3
2
+3+3
3
2
,
3
2
?3+3
3
2
).
【考点】待定系数法求一次函数解析式,待定系数法求二次函数解析式,二次函数与一次函数的综合应用
【解析】【分析】(1)根据二次函数的顶点坐标设出顶点式,根据抛物线经过原点,将原点坐标代入即可求出解析式; (2)设E(m,0),然后用含m的式子表示出点B和点C的坐标,根据E′在抛物线上,可知E、B关于对称轴对称,进而根据点E和点B到对称轴的距离相等列式,求出m的值,得到点B和点C的坐标,即可求出直线l′ 的解析式; (3)分两种情况分析:①当P1与N重合时,△P1B′N′是等腰三角形;②当N′=N′B′时,设P(m,m﹣3),然后利用勾股定理求出m的值,即可得解.
28.【答案】(1)点M? (1)经过t秒时,/, /, 则/, / ∵/=/=/, ∴/??? ∴/?? ∴//? ∴/? ∵/∴当/时,S的值最大. (1)存在。 设经过t秒时,NB=t,OM="2t" ,则/, /∴/=/=/? ①若/, 则/是等腰Rt△/底边/上的高, ∴/是底边/的中线???? ∴/, ∴/, ∴/, ??????? ∴点/的坐标为(1,0) ②若/, 此时/与/重合,∴/, ∴/, ∴/????????? ∴点/的坐标为(2,0)
【考点】二次函数的最值,勾股定理
【解析】【分析】 (1)由于点M比点N先出发并且点M的速度比点N大,可知点M能到达终点. (2)经过t秒时可得NB=y,OM-2t.根据∠BCA=∠MAQ=45°推出QN=CN,PQ的值.求出S与t的函数关系式后根据t的值求出S的最大值. (3)本题分两种情况讨论(若∠AQM=90°,PQ是等腰Rt△MQA底边MA上的高; 若∠QMA=90°,QM与QP重合)求出t值.
