人教B版选修2-2 1.4.2 微积分基本定理 课件(22张)
文档属性
| 名称 | 人教B版选修2-2 1.4.2 微积分基本定理 课件(22张) |  | |
| 格式 | zip | ||
| 文件大小 | 459.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-01-19 11:37:13 | ||
图片预览






文档简介
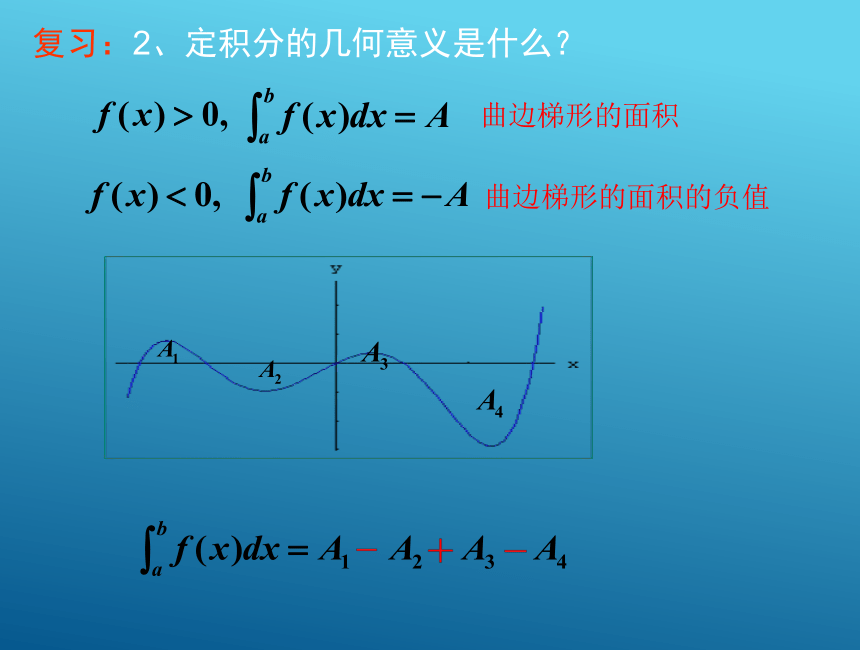
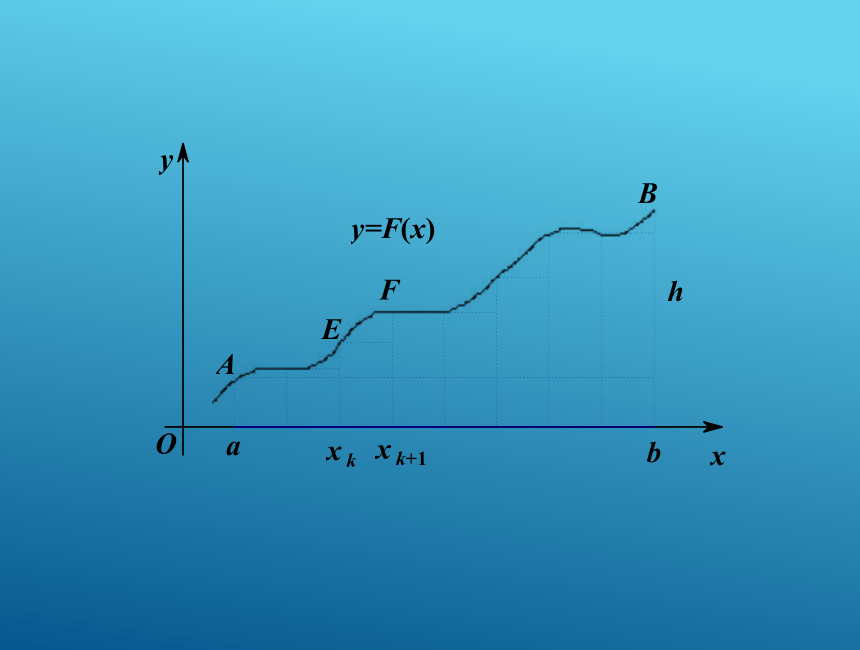
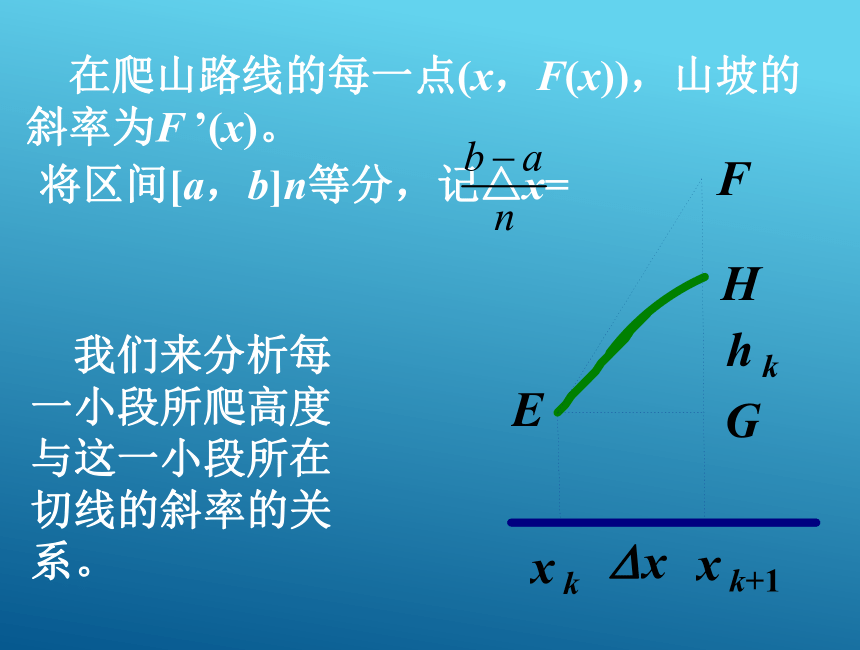
课件22张PPT。高中数学人教版选修2-2第一章第四节微积分基本定理积分上限积分下限复习:1、定积分是怎样定义?定积分的简单性质曲边梯形的面积曲边梯形的面积的负值复习:2、定积分的几何意义是什么?复习引入:定积分的几何意义的应用8微积分基本定理 在爬山路线的每一点(x,F(x)),山坡的斜率为F ’(x)。将区间[a,b]n等分,记△x= 我们来分析每一小段所爬高度与这一小段所在切线的斜率的关系。 即F(xk+1)-F(xk)≈F ’(xk)△x. 这样,我们得到了一系列近似等式:
h1=F(a+△x)-F(a) ≈F ’(a)△x,
h2=F(a+2△x)-F(a+△x)≈F’(a+△x)△x,
h3=F(a+3△x)-F(a+2△x)≈F’(a+2△x)△x,
…………
hn-1=F[a+(n-1)△x]-[(a+(n-2)△x)
≈F ’[a+(n-2))△x]△x,
hn=F(b)-F[a+(n-1)△x)
≈F ’[a+(n-1)△x]△x,微积分基本定理 如果F ’(x)=f(x),且f(x)在[a,b]上可积,则 其中F(x)叫做f(x)的一个原函数。 由于[F(x)+C]’=f(x),F(x)+C也是f(x)的原函数。其中C为常数。 一般地,原函数在[a,b]上的改变量F(b)-F(a)简记作F(x) ,因此微积分基本定理可以写成形式:微积分基本定理:这个结论叫微积分基本定理(fundamental theorem of calculus),又叫牛顿-莱布尼茨公式(Newton-Leibniz Formula).莱布尼兹莱布尼兹,德国数学家、哲学家,和牛顿
同为微积分的创始人;1646年7月1日生于
莱比锡,1716年11月14日卒于德国的汉诺
威。他父亲是莱比锡大学伦理学教授,家
庭丰富的藏书引起他广泛的兴趣。1661年
入莱比锡大学学习法律,又曾到耶拿大学
学习几何,1666年在纽伦堡阿尔特多夫取得法学博士学位。他当时写的论文《论组合的技巧》已含有数理逻
辑的早期思想,后来的工作使他成为数理逻辑的创始人。
1667年他投身外交界,曾到欧洲各国游历。1676年到汉
诺威,任腓特烈公爵顾问及图书馆的馆长,并常居汉诺威,直到去世。莱布尼兹的多才多艺在历史上很少有
人能和他相比,他的著作包括数学、历史、语言、生物
、地质、机械、物理、法律、外交等各个方面。返回微积分基本定理:说明:
牛顿-莱布尼茨公式提供了计算定积分的简便的基本方法,即求定积分的值,只要求出被积函数 f(x)的一个原函数F(x),然后计算原函数在区间[a,b]上的增量F(b)–F(a)即可.该公式把计算定积分归结为求原函数的问题。例1 计算下列定积分 练习1:定积分公式:例3例4:求曲线1.微积分基本定理:2.基本初等函数的原函数公式谢谢观赏!
h1=F(a+△x)-F(a) ≈F ’(a)△x,
h2=F(a+2△x)-F(a+△x)≈F’(a+△x)△x,
h3=F(a+3△x)-F(a+2△x)≈F’(a+2△x)△x,
…………
hn-1=F[a+(n-1)△x]-[(a+(n-2)△x)
≈F ’[a+(n-2))△x]△x,
hn=F(b)-F[a+(n-1)△x)
≈F ’[a+(n-1)△x]△x,微积分基本定理 如果F ’(x)=f(x),且f(x)在[a,b]上可积,则 其中F(x)叫做f(x)的一个原函数。 由于[F(x)+C]’=f(x),F(x)+C也是f(x)的原函数。其中C为常数。 一般地,原函数在[a,b]上的改变量F(b)-F(a)简记作F(x) ,因此微积分基本定理可以写成形式:微积分基本定理:这个结论叫微积分基本定理(fundamental theorem of calculus),又叫牛顿-莱布尼茨公式(Newton-Leibniz Formula).莱布尼兹莱布尼兹,德国数学家、哲学家,和牛顿
同为微积分的创始人;1646年7月1日生于
莱比锡,1716年11月14日卒于德国的汉诺
威。他父亲是莱比锡大学伦理学教授,家
庭丰富的藏书引起他广泛的兴趣。1661年
入莱比锡大学学习法律,又曾到耶拿大学
学习几何,1666年在纽伦堡阿尔特多夫取得法学博士学位。他当时写的论文《论组合的技巧》已含有数理逻
辑的早期思想,后来的工作使他成为数理逻辑的创始人。
1667年他投身外交界,曾到欧洲各国游历。1676年到汉
诺威,任腓特烈公爵顾问及图书馆的馆长,并常居汉诺威,直到去世。莱布尼兹的多才多艺在历史上很少有
人能和他相比,他的著作包括数学、历史、语言、生物
、地质、机械、物理、法律、外交等各个方面。返回微积分基本定理:说明:
牛顿-莱布尼茨公式提供了计算定积分的简便的基本方法,即求定积分的值,只要求出被积函数 f(x)的一个原函数F(x),然后计算原函数在区间[a,b]上的增量F(b)–F(a)即可.该公式把计算定积分归结为求原函数的问题。例1 计算下列定积分 练习1:定积分公式:例3例4:求曲线1.微积分基本定理:2.基本初等函数的原函数公式谢谢观赏!
