北师大版数学九年级下册2.4二次函数的应用课件(19张PPT)
文档属性
| 名称 | 北师大版数学九年级下册2.4二次函数的应用课件(19张PPT) |
|
|
| 格式 | zip | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-01-20 00:00:00 | ||
图片预览






文档简介
初中数学 九年级下册 北师大版
1、抛物线y=x2- 4x+3的顶点坐标是_____,当x=___时,函数y有最_____值是___。
2、抛物线y=x2- 4x+3, 对称轴是______,当x>2时,y随x的增大而____;
当-1<x≤1时, y随x的增大而____, 在此情况下x=___时,函数取最小值是___,
(2,—1)
2
—1
小
0
1
直线x=2
增大
减小
跳绳时,绳甩到最低处的形状是抛物线。正在甩绳的两名同学的间距AB=6米。他们的手到地面的距离AO和BD均为0.3米,以0为原点建立平面直角坐标系,设此抛物线的表达式为
y=a(x – 3)2
1、求出抛物线的表达式.
2、若跳绳同学的队伍长4米,正对着甲同学站好,则排头同学最好站在哪个点处?(写出这个点的坐标。)此时他至少要跳过几米才能不被绳绊倒?
A B
0 1 2 3 4 5 6 D
甲 乙
M
把点A(0,0.3)代入 y=a(x – 3)2中得,
0.3=9a
a=1/30
∴y=1/30(x – 3)2
青岛出口加工区经销一种水产品,每千克成本为50元,市场调查发现,在一段时间内,销售量y(千克)与销售单价x(元/千克)之间的关系可近似地看做一次函数为: y=-2x+240.
(1)公司这段时间内获得利润为w(元),销售单价定为多少元时,这段时间销售利润最大?
青岛出口加工区经销一种水产品,每千克成本为50元 ,市场调查发现,在一段时间内,销售量y(千克)与销售单价x(元/千克)之间的关系
可近似地看做一次函数为:w=-2x+240.
(1) 公司这段时间内获得利润为w(元),销售单价定为多少元时,这段时间销售利润最大?
是一次函数的关系。
售价x(元/千克) …… 55 60 65 ……
销售量y(千克) …… 130 120 110 ……
解:设y=kx+b(k,b为常数,且k不等于0)
∴一次函数关系式为:y=-2x+240
售价x(元/千克) …… 55 60 65 ……
销售量y(千克) …… 130 120 110 ……
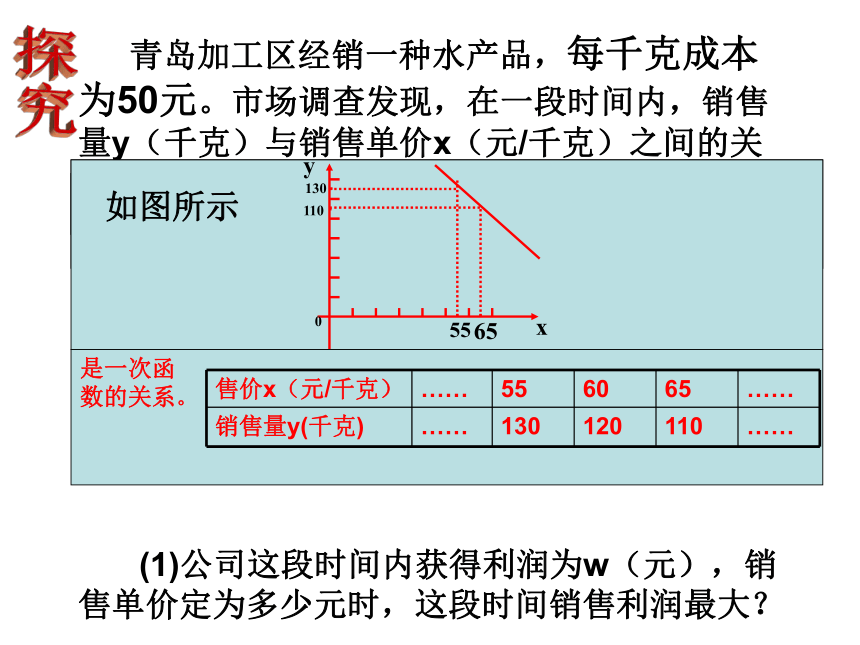
青岛加工区经销一种水产品,每千克成本为50元。市场调查发现,在一段时间内,销售量y(千克)与销售单价x(元/千克)之间的关系
可近似地看做一次函数为:w=-2x+240.
(1)公司这段时间内获得利润为w(元),销售单价定为多少元时,这段时间销售利润最大?
w=-2x+240
是一次函数的关系。
如图所示
是一次函数的关系。
售价x(元/千克) …… 55 60 65 ……
销售量y(千克) …… 130 120 110 ……
售价x(元/千克) …… 55 60 65 ……
销售量y(千克) …… 130 120 110 ……
青岛出口加工区经销一种水产品,每千克成本为50元。市场调查发现,在一段时间内,销售量y(千克)与销售单价x(元/千克)之间的关系可近似地看做一次函数为: y=-2x+240.
(3)如果物价部门规定销售单价不得高于90元/千克,公司想要获得2250元的销售利润,销售单价应定为多少?
(4)公司想要在这段时间内获得不少于2250元的销售利润,销售单价应在什么范围内?
(2)如果在售价不高于80元的情况下公司要获得最大利润,售价定为多少元?
如果售价不低于90元不高于100元呢?
利润率不得高于60%
(1)公司这段时间内获得利润为w(元),销售单价定为
多少元时,这段时间销售利润最大?
75
95
何时用方程解决问题?
何时用不等式解决问题?
何时用图像法解决问题?
何时用函数解决问题?
我总结我进步
青岛出口加工区经销一种水产品,每千克成本为50元。市场调查发现,在一段时间内,销售量y(千克)与销售单价x(元/千克)之间的关系可近似地看做一次函数为: y=-2x+240.
(3)如果物价部门规定销售单价不得高于90元/千克,公司想要获得2250元的销售利润,销售单价应定为多少?
(4)公司想要在这段时间内获得不少于2250元的销售利润,销售单价应在什么范围内?
(2)如果在售价不高于80元的情况下公司要获得最大利润,售价定为多少元?
(5)在售价不高于80元的情况下,如果要使得利润不低于2250元,那么他每月的成本最少需要多少元?
如果90≤ x≤100呢?
(5)在售价不高于80元的情况下,如果要使得利润不低于2250元,那么他每月的成本最少需要多少元?
∵w≥2250
∴75 ≤ x ≤95
又∵x ≤80
∴ 75 ≤ x ≤80
成本
青岛出口加工区经销一种水产品,每千克成本为50元。市场调查发现,在一段时间内,销售量y(千克)与销售单价x(元/千克)之间的关系可近似地看做一次函数为: y=-2x+240.
销售量
(5)在售价不高于80元的情况下,如果要使得利润不低于2250元,那么他每月的成本最少需要多少元?
∵w≥2250
∴75 ≤ x ≤95
又∵x ≤80
∴ 75 ≤ x ≤80
青岛出口加工区经销一种水产品,每千克成本为50元。市场调查发现,在一段时间内,销售量y(千克)与销售单价x(元/千克)之间的关系可近似地看做一次函数为: y=-2x+240.
设每月的成本为z元
Z=50(-2x+240)
= -100x+12000
∵ k<0,z随x的增大而减小
∴ X=80时,z最小
=4000
(5)在售价不高于80元的情况下,如果要使得利润不低于2250元,那么他每月的成本最少需要多少元?
∵w≥2250
∴75 ≤ x ≤95
又∵x ≤80
∴ 75 ≤ x ≤80
青岛出口加工区经销一种水产品,每千克成本为50元。市场调查发现,在一段时间内,销售量y(千克)与销售单价x(元/千克)之间的关系可近似地看做一次函数为: y=-2x+240.
∵ y=-2x+240
K<0,y随x的增大而减小
当x = 80时,y最小
=80
∵当进价一定时,销售量越小,成本越小,
50×80=4000
青岛加工区企划部为指导某种水产品的养殖和销售,对历年市场行情和水产品养殖情况进行了调查,调查发现这种水产品每千克售价y1(元)与销售月份x(月)满足关系式 而其 每千克成本y2(元)与销售月份x(月)满足的函数关系如图.
(1)试确定b、c的值
(3)“五·一”之前,几月份出售这种水产品每千克的利 润最大?
(2)求出这种水产品每千克的
利润(元)与销售月份(月)
之间的函数关系式;
Y2=1/8x2+bx+c
1
我市休渔期期间,几月份出售每千克利润最大?
若每千克售价不得高于33元,几月份出售每千克利润最大?
y
在5月——8月期间,几月份出售每千克的利润最小?
友情提示:我市休渔期为6月1号——9月1号
1、本节课有什么收获?
2、今后解决问题应该注意哪些方面?
3、给你印象最深的题目是……
愿老师们:心想事成!
祝同学们:金榜题名!
生活中时时有数学,事事有数学;
让我们爱数学、学数学、用数学!
2、有一种可食用的野生菌,上市时,外商李经理按市场价格30元/千克收购了这种野生菌1000千克存放入冷库中,据预测,该野生菌的市场价格将以每天每千克上涨1元;但冷冻存放这批野生菌时每天需要支出各种费用合计310元,而且这类野生菌在冷库中最多保存80天,同时,平均每天有3千克的野生菌损坏不能出售.
(1)设x天后每千克该野生菌的市场价格为y元,试写出y与x之间的函数关系式.
(2)若存放x天后,将这批野生菌一次性出售,设这批野生菌的销售总额p为元,试写出p与x之间的函数关系式.
(3)李经理将这批野生茵存放多少天后出售可获得最大利润?
(利润=销售总额-收购成本-各种费用)
1、 有一个抛物线形的拱桥,这个桥的跨度为40米。以点A为坐标原点建立平面直角坐标系,设抛物线的表达式为y= — 1/40 x2+bx+c,建筑工人想在跨度中心M点处垂直竖立一铁柱支撑拱顶,问这根铁柱应取多长?
1、抛物线y=x2- 4x+3的顶点坐标是_____,当x=___时,函数y有最_____值是___。
2、抛物线y=x2- 4x+3, 对称轴是______,当x>2时,y随x的增大而____;
当-1<x≤1时, y随x的增大而____, 在此情况下x=___时,函数取最小值是___,
(2,—1)
2
—1
小
0
1
直线x=2
增大
减小
跳绳时,绳甩到最低处的形状是抛物线。正在甩绳的两名同学的间距AB=6米。他们的手到地面的距离AO和BD均为0.3米,以0为原点建立平面直角坐标系,设此抛物线的表达式为
y=a(x – 3)2
1、求出抛物线的表达式.
2、若跳绳同学的队伍长4米,正对着甲同学站好,则排头同学最好站在哪个点处?(写出这个点的坐标。)此时他至少要跳过几米才能不被绳绊倒?
A B
0 1 2 3 4 5 6 D
甲 乙
M
把点A(0,0.3)代入 y=a(x – 3)2中得,
0.3=9a
a=1/30
∴y=1/30(x – 3)2
青岛出口加工区经销一种水产品,每千克成本为50元,市场调查发现,在一段时间内,销售量y(千克)与销售单价x(元/千克)之间的关系可近似地看做一次函数为: y=-2x+240.
(1)公司这段时间内获得利润为w(元),销售单价定为多少元时,这段时间销售利润最大?
青岛出口加工区经销一种水产品,每千克成本为50元 ,市场调查发现,在一段时间内,销售量y(千克)与销售单价x(元/千克)之间的关系
可近似地看做一次函数为:w=-2x+240.
(1) 公司这段时间内获得利润为w(元),销售单价定为多少元时,这段时间销售利润最大?
是一次函数的关系。
售价x(元/千克) …… 55 60 65 ……
销售量y(千克) …… 130 120 110 ……
解:设y=kx+b(k,b为常数,且k不等于0)
∴一次函数关系式为:y=-2x+240
售价x(元/千克) …… 55 60 65 ……
销售量y(千克) …… 130 120 110 ……
青岛加工区经销一种水产品,每千克成本为50元。市场调查发现,在一段时间内,销售量y(千克)与销售单价x(元/千克)之间的关系
可近似地看做一次函数为:w=-2x+240.
(1)公司这段时间内获得利润为w(元),销售单价定为多少元时,这段时间销售利润最大?
w=-2x+240
是一次函数的关系。
如图所示
是一次函数的关系。
售价x(元/千克) …… 55 60 65 ……
销售量y(千克) …… 130 120 110 ……
售价x(元/千克) …… 55 60 65 ……
销售量y(千克) …… 130 120 110 ……
青岛出口加工区经销一种水产品,每千克成本为50元。市场调查发现,在一段时间内,销售量y(千克)与销售单价x(元/千克)之间的关系可近似地看做一次函数为: y=-2x+240.
(3)如果物价部门规定销售单价不得高于90元/千克,公司想要获得2250元的销售利润,销售单价应定为多少?
(4)公司想要在这段时间内获得不少于2250元的销售利润,销售单价应在什么范围内?
(2)如果在售价不高于80元的情况下公司要获得最大利润,售价定为多少元?
如果售价不低于90元不高于100元呢?
利润率不得高于60%
(1)公司这段时间内获得利润为w(元),销售单价定为
多少元时,这段时间销售利润最大?
75
95
何时用方程解决问题?
何时用不等式解决问题?
何时用图像法解决问题?
何时用函数解决问题?
我总结我进步
青岛出口加工区经销一种水产品,每千克成本为50元。市场调查发现,在一段时间内,销售量y(千克)与销售单价x(元/千克)之间的关系可近似地看做一次函数为: y=-2x+240.
(3)如果物价部门规定销售单价不得高于90元/千克,公司想要获得2250元的销售利润,销售单价应定为多少?
(4)公司想要在这段时间内获得不少于2250元的销售利润,销售单价应在什么范围内?
(2)如果在售价不高于80元的情况下公司要获得最大利润,售价定为多少元?
(5)在售价不高于80元的情况下,如果要使得利润不低于2250元,那么他每月的成本最少需要多少元?
如果90≤ x≤100呢?
(5)在售价不高于80元的情况下,如果要使得利润不低于2250元,那么他每月的成本最少需要多少元?
∵w≥2250
∴75 ≤ x ≤95
又∵x ≤80
∴ 75 ≤ x ≤80
成本
青岛出口加工区经销一种水产品,每千克成本为50元。市场调查发现,在一段时间内,销售量y(千克)与销售单价x(元/千克)之间的关系可近似地看做一次函数为: y=-2x+240.
销售量
(5)在售价不高于80元的情况下,如果要使得利润不低于2250元,那么他每月的成本最少需要多少元?
∵w≥2250
∴75 ≤ x ≤95
又∵x ≤80
∴ 75 ≤ x ≤80
青岛出口加工区经销一种水产品,每千克成本为50元。市场调查发现,在一段时间内,销售量y(千克)与销售单价x(元/千克)之间的关系可近似地看做一次函数为: y=-2x+240.
设每月的成本为z元
Z=50(-2x+240)
= -100x+12000
∵ k<0,z随x的增大而减小
∴ X=80时,z最小
=4000
(5)在售价不高于80元的情况下,如果要使得利润不低于2250元,那么他每月的成本最少需要多少元?
∵w≥2250
∴75 ≤ x ≤95
又∵x ≤80
∴ 75 ≤ x ≤80
青岛出口加工区经销一种水产品,每千克成本为50元。市场调查发现,在一段时间内,销售量y(千克)与销售单价x(元/千克)之间的关系可近似地看做一次函数为: y=-2x+240.
∵ y=-2x+240
K<0,y随x的增大而减小
当x = 80时,y最小
=80
∵当进价一定时,销售量越小,成本越小,
50×80=4000
青岛加工区企划部为指导某种水产品的养殖和销售,对历年市场行情和水产品养殖情况进行了调查,调查发现这种水产品每千克售价y1(元)与销售月份x(月)满足关系式 而其 每千克成本y2(元)与销售月份x(月)满足的函数关系如图.
(1)试确定b、c的值
(3)“五·一”之前,几月份出售这种水产品每千克的利 润最大?
(2)求出这种水产品每千克的
利润(元)与销售月份(月)
之间的函数关系式;
Y2=1/8x2+bx+c
1
我市休渔期期间,几月份出售每千克利润最大?
若每千克售价不得高于33元,几月份出售每千克利润最大?
y
在5月——8月期间,几月份出售每千克的利润最小?
友情提示:我市休渔期为6月1号——9月1号
1、本节课有什么收获?
2、今后解决问题应该注意哪些方面?
3、给你印象最深的题目是……
愿老师们:心想事成!
祝同学们:金榜题名!
生活中时时有数学,事事有数学;
让我们爱数学、学数学、用数学!
2、有一种可食用的野生菌,上市时,外商李经理按市场价格30元/千克收购了这种野生菌1000千克存放入冷库中,据预测,该野生菌的市场价格将以每天每千克上涨1元;但冷冻存放这批野生菌时每天需要支出各种费用合计310元,而且这类野生菌在冷库中最多保存80天,同时,平均每天有3千克的野生菌损坏不能出售.
(1)设x天后每千克该野生菌的市场价格为y元,试写出y与x之间的函数关系式.
(2)若存放x天后,将这批野生菌一次性出售,设这批野生菌的销售总额p为元,试写出p与x之间的函数关系式.
(3)李经理将这批野生茵存放多少天后出售可获得最大利润?
(利润=销售总额-收购成本-各种费用)
1、 有一个抛物线形的拱桥,这个桥的跨度为40米。以点A为坐标原点建立平面直角坐标系,设抛物线的表达式为y= — 1/40 x2+bx+c,建筑工人想在跨度中心M点处垂直竖立一铁柱支撑拱顶,问这根铁柱应取多长?
