2018-2019学年新人教版九年级数学下册 28.2.解直角三角形 课件 (20张PPT)
文档属性
| 名称 | 2018-2019学年新人教版九年级数学下册 28.2.解直角三角形 课件 (20张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 4.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-01-20 15:22:39 | ||
图片预览






文档简介
课题
目标
1. 理解在直角三角形中除直角外其余五个元素之间的关系,了解确定一个三角形和解直角三角形所需条件的一致性.
2. 体会从一般到特殊的思考方法,掌握解直角三角形的几种基本的类型,会选择合理的算法.
3.通过共同探索,认识分类讨论、化归等数学思想,激发探索数学的热情,树立学习数学的信心.
目标
2. 体会从一般到特殊的思考方法,掌握解直角三角形的几种基本的类型,会选择合理的算法.
温故知新
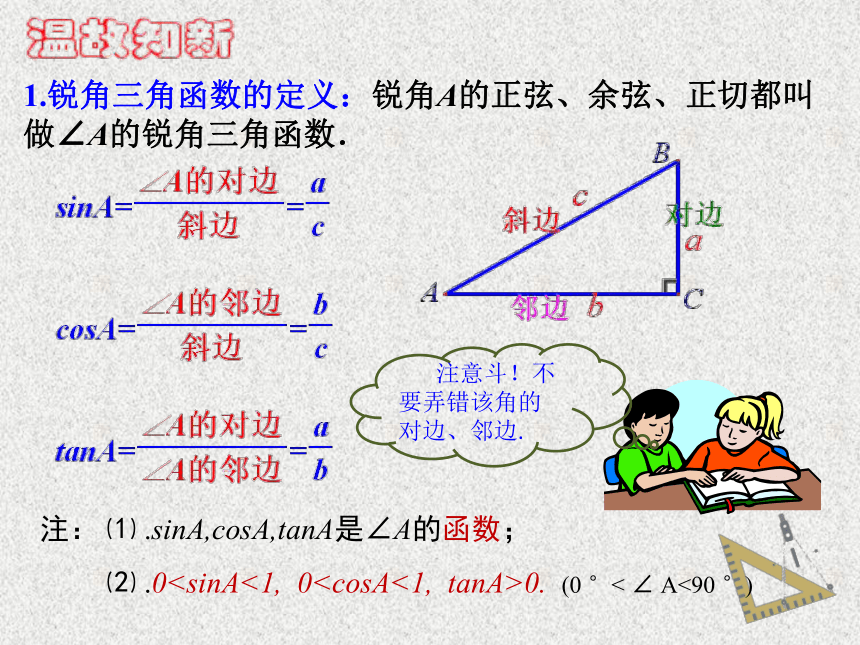
1.锐角三角函数的定义:锐角A的正弦、余弦、正切都叫做∠A的锐角三角函数.
注: ⑴ .sinA,cosA,tanA是∠A的函数;
⑵ .00. (0 °< ∠ A<90 °)
注意斗!不要弄错该角的对边、邻边.
图
示
法
口
诀
法
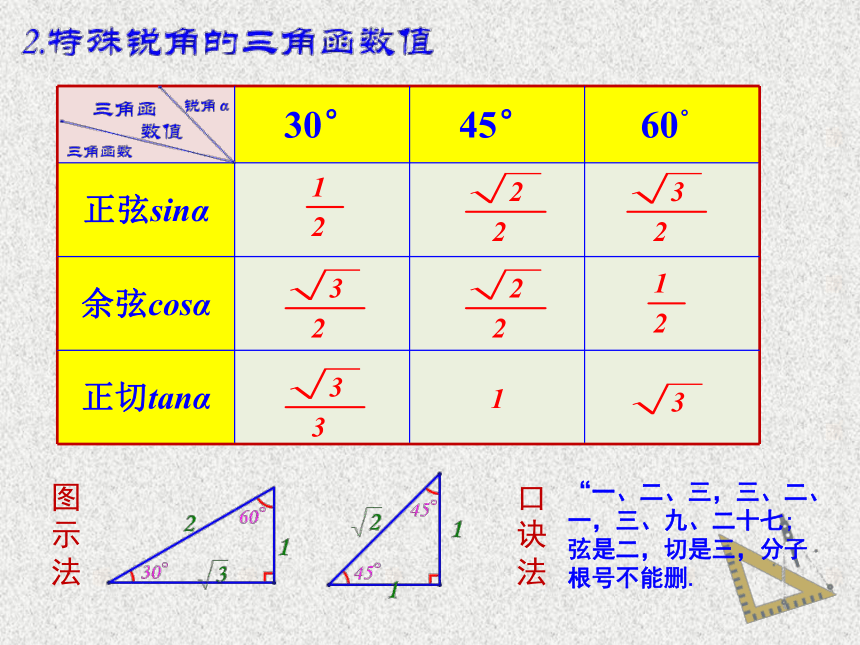
“一、二、三,三、二、一,三、九、二十七;弦是二,切是三,分子根号不能删.
温故知新(续)
30° 45° 60°
正弦sinα
余弦cosα
正切tanα
引入
解疑答惑
BC ≈ 5.2m
AB ≈ 54.5m
在Rt △ACB中有:
利用计算器求得:
说明:
图片中测得的数据来自教材和网络,据说现在“扶直”后倾斜角度约为3.99 °,以前约为5.5 °,答案仅供参考!
如图(见教材72页引入材料比萨斜塔),∠C = 90°, AC为垂直中心线,AB为塔身中心线.
即约为
如果将“新课引入”的问题抽象为数学问题,就是已知直角三角形的斜边和一直角边,求它的锐角的度数.
定义:由直角三角形的已知元素,求出其余未知元素的过程,叫做解直角三角形.
如图,在Rt △ACB中, ∠C=90 °; ∠A、∠B、∠C所对的边分别为a、b、c.
⑴.三边之间的关系:
(勾股定理)
⑵.两锐角之间的关系:
(直角三角形两锐角互余)
⑶.边角之间的关系:
讲授新课
利用上面这些关系,可以“知二求三”(直角除外,且已知中至少要有一条边).
类型一
类型一.已知直角三角形两直角边长,解直角三角形.
分析:
本题已知的是两直角边,这种情况经常从其中一个锐角的正切函数入手,先求出该锐角,再根据边角关系进一步求出余下的两个未知元素.
略解:在Rt△ACB中, ∠C=90°
类型二
类型二.已知直角三角形的一直角边长和斜边长,解直角三角形.
分析:
本题已知的是一直角边和斜边长,这种情况可以从其中一个锐角的正弦(或余弦)函数入手,先求出该锐角,再根据边角关系进一步求出余下的两个未知元素.
略解:在Rt△ACB中, ∠C=90°
类型三
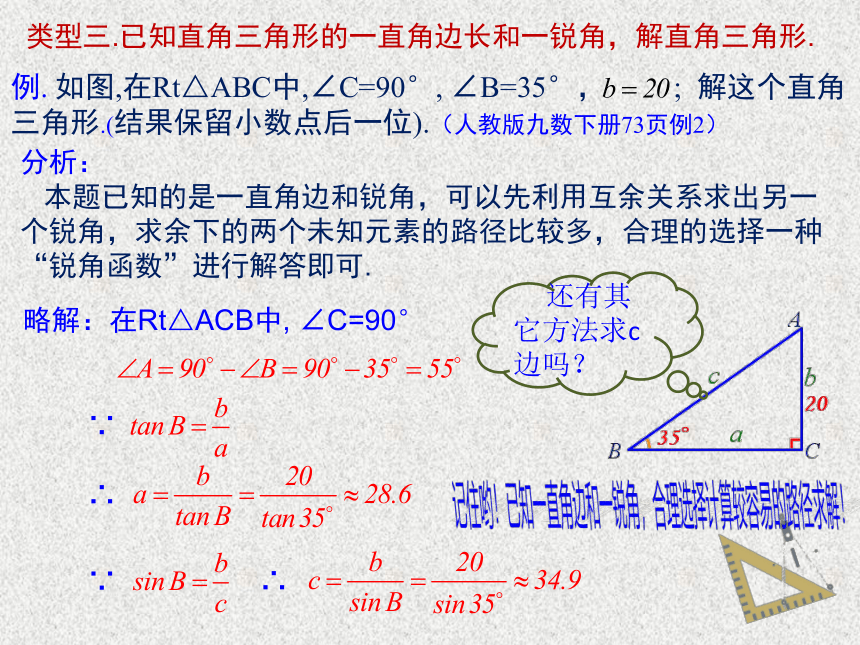
类型三.已知直角三角形的一直角边长和一锐角,解直角三角形.
分析:
本题已知的是一直角边和锐角,可以先利用互余关系求出另一个锐角,求余下的两个未知元素的路径比较多,合理的选择一种“锐角函数”进行解答即可.
略解:在Rt△ACB中, ∠C=90°
还有其它方法求c边吗?
类型四.已知直角三角形的斜边长和一锐角,解直角三角形.
类型四
分析:
本题已知的是斜边长和锐角,可以先利用互余关系求出另一个锐角,求余下的两个未知元素的路径比较多,合理的选择一种“锐角函数”进行解答即可.
略解:在Rt△ACB中, ∠C=90°
还有其它方法求a,b边吗?
追踪练习
1.在下列直角三形中,不能求解的是 ( )
A.已知一直角边一锐角 B.已知一斜边一锐角
C.已知两边 D.已知两角
D
2.在Rt△ABC中∠C=90°,已知a边及∠A,则斜边应为(? ?)?
3.有一个角是30°的直角三角形,斜边为1cm,则斜边上的高为 (?? )?
4.等腰三角形底边与底边上的高的比是2:3,则底角的余弦值为 (?? )?
A
C
D
5.在Rt△ABC中,∠ C=90 °; 若AC=9,cosB=0.8,则AB等于 .
追踪练习(续)
7.在△ABC中,∠C=90°,c = 2, ∠B = 30°, 解这个直角三角形 .
归纳总结(列表)
一.列表归纳解直角三角形的基本类型
图示和条件 解答路径参考
已知两边 已知两直角边
已知一直角边和一斜边
已知一边一锐角 已知一锐角和一直角边
已知一锐角和一斜边
归纳总结(口诀)
知斜边,求直边,
知直边,求直边,
知两边,求一边,
知两边,求一角,
知锐角,求锐角,
知直边,求斜边,
好方法,要选择,
正余弦,很方便;
用正切,理当然;
边角式,要选好;
用勾股,最方便;
用互余,最可靠;
用除法,正余弦;
能用乘,不用除.
解直角三角形的方法一般遵循“有斜用弦,无斜用切”的原则.
注:以上“三字经口诀” 来源于网络资源,供同学们解答时参考.
二.解直角三角形优选关系式的“三字经口诀”
拓展提升(例1)
例1.如图,在正方形网格中,圆与网格线相切于格点处,其余的条件见图,根据图示求出∠1的度数.(结果保留小数点后一位.)
分析:要直接求∠1的度的正弦值比较困难,但可以通过“同弧或等弧所对的圆周角相等”进行转化,在把问题化归在网格构成的直角三角形中,用解直角三角形的思路来解决问题.
略解:
设网格中每个小正方形的边长为单位1,则AC=3,BC=1.
在Rt △ACB中,根据勾股定理有:
还有其它途径求∠1的度数吗?
拓展提升(例2)
分析:求DC的长可以化归在Rt△DCB中,根据题中条件需求出一边长才能解决问题;过D点作△ABD的边AB的垂线段,通过直角三角形的边角关系可以求出BD,问题便解决了.
略解:
过D作DE ⊥ AB于E.
∴ ∠AED = ∠BED = 90 °
∵∠A = 30°,AD=4
∵∠ADE = 90°-30°=60°,且∠ADB=105°
∴ ∠EDB = 105°- 60 °=45°
∵在Rt△DCB中有
∴ ∠BDC= 60 °
∴ ∠DBC= 30 °
拓展提升(例3)
分析:本题通过第一个方程可以求出∠A的正弦值,通过第二个方程可以求出直角三角形斜边c的长度;结合∠A的正弦值可以求出a边的值,再利用勾股定理b边的值.
略解:
由第一个方程结合题意可得:
整理配方为:
解得:
由第二个方程结合题意可得:
解得:
(不合题意,舍去)
根据题意和前面的解答画出示意图.
∵∠C = 90°
课外选练
课外选练不提供参考解答!
谈谈收获!
1. 如图,在Rt △ACB中, ∠C=90 °; ∠A、∠B、∠C所对的边分别为a、b、c.
⑴.三边之间的关系:
(勾股定理)
⑵.两锐角之间的关系:
(直角三角形两锐角互余)
⑶.边角之间的关系:
利用上面这些关系,可以“知二求三”(直角除外,已知中至少要有一条边).
2. 解直角三角形基本类型
⑴. 已知两边: ①.已知两直角边; ②.已知一直角边和斜边.
⑵. 已知一角一边: ①.已知一锐角和一直角边; ②.已知一锐角和斜边.
解答时请注意“有斜用弦,无斜用切”.
1.书上28.2.74页练习题,28.2.79页习题2、5题;
2.《锐角三角函数》训练题余弦正切函数部分选做.
作业布置
书面作业:
再
见
!
课外探究:
《课外选练》1、2、3、4题.
目标
1. 理解在直角三角形中除直角外其余五个元素之间的关系,了解确定一个三角形和解直角三角形所需条件的一致性.
2. 体会从一般到特殊的思考方法,掌握解直角三角形的几种基本的类型,会选择合理的算法.
3.通过共同探索,认识分类讨论、化归等数学思想,激发探索数学的热情,树立学习数学的信心.
目标
2. 体会从一般到特殊的思考方法,掌握解直角三角形的几种基本的类型,会选择合理的算法.
温故知新
1.锐角三角函数的定义:锐角A的正弦、余弦、正切都叫做∠A的锐角三角函数.
注: ⑴ .sinA,cosA,tanA是∠A的函数;
⑵ .0
注意斗!不要弄错该角的对边、邻边.
图
示
法
口
诀
法
“一、二、三,三、二、一,三、九、二十七;弦是二,切是三,分子根号不能删.
温故知新(续)
30° 45° 60°
正弦sinα
余弦cosα
正切tanα
引入
解疑答惑
BC ≈ 5.2m
AB ≈ 54.5m
在Rt △ACB中有:
利用计算器求得:
说明:
图片中测得的数据来自教材和网络,据说现在“扶直”后倾斜角度约为3.99 °,以前约为5.5 °,答案仅供参考!
如图(见教材72页引入材料比萨斜塔),∠C = 90°, AC为垂直中心线,AB为塔身中心线.
即约为
如果将“新课引入”的问题抽象为数学问题,就是已知直角三角形的斜边和一直角边,求它的锐角的度数.
定义:由直角三角形的已知元素,求出其余未知元素的过程,叫做解直角三角形.
如图,在Rt △ACB中, ∠C=90 °; ∠A、∠B、∠C所对的边分别为a、b、c.
⑴.三边之间的关系:
(勾股定理)
⑵.两锐角之间的关系:
(直角三角形两锐角互余)
⑶.边角之间的关系:
讲授新课
利用上面这些关系,可以“知二求三”(直角除外,且已知中至少要有一条边).
类型一
类型一.已知直角三角形两直角边长,解直角三角形.
分析:
本题已知的是两直角边,这种情况经常从其中一个锐角的正切函数入手,先求出该锐角,再根据边角关系进一步求出余下的两个未知元素.
略解:在Rt△ACB中, ∠C=90°
类型二
类型二.已知直角三角形的一直角边长和斜边长,解直角三角形.
分析:
本题已知的是一直角边和斜边长,这种情况可以从其中一个锐角的正弦(或余弦)函数入手,先求出该锐角,再根据边角关系进一步求出余下的两个未知元素.
略解:在Rt△ACB中, ∠C=90°
类型三
类型三.已知直角三角形的一直角边长和一锐角,解直角三角形.
分析:
本题已知的是一直角边和锐角,可以先利用互余关系求出另一个锐角,求余下的两个未知元素的路径比较多,合理的选择一种“锐角函数”进行解答即可.
略解:在Rt△ACB中, ∠C=90°
还有其它方法求c边吗?
类型四.已知直角三角形的斜边长和一锐角,解直角三角形.
类型四
分析:
本题已知的是斜边长和锐角,可以先利用互余关系求出另一个锐角,求余下的两个未知元素的路径比较多,合理的选择一种“锐角函数”进行解答即可.
略解:在Rt△ACB中, ∠C=90°
还有其它方法求a,b边吗?
追踪练习
1.在下列直角三形中,不能求解的是 ( )
A.已知一直角边一锐角 B.已知一斜边一锐角
C.已知两边 D.已知两角
D
2.在Rt△ABC中∠C=90°,已知a边及∠A,则斜边应为(? ?)?
3.有一个角是30°的直角三角形,斜边为1cm,则斜边上的高为 (?? )?
4.等腰三角形底边与底边上的高的比是2:3,则底角的余弦值为 (?? )?
A
C
D
5.在Rt△ABC中,∠ C=90 °; 若AC=9,cosB=0.8,则AB等于 .
追踪练习(续)
7.在△ABC中,∠C=90°,c = 2, ∠B = 30°, 解这个直角三角形 .
归纳总结(列表)
一.列表归纳解直角三角形的基本类型
图示和条件 解答路径参考
已知两边 已知两直角边
已知一直角边和一斜边
已知一边一锐角 已知一锐角和一直角边
已知一锐角和一斜边
归纳总结(口诀)
知斜边,求直边,
知直边,求直边,
知两边,求一边,
知两边,求一角,
知锐角,求锐角,
知直边,求斜边,
好方法,要选择,
正余弦,很方便;
用正切,理当然;
边角式,要选好;
用勾股,最方便;
用互余,最可靠;
用除法,正余弦;
能用乘,不用除.
解直角三角形的方法一般遵循“有斜用弦,无斜用切”的原则.
注:以上“三字经口诀” 来源于网络资源,供同学们解答时参考.
二.解直角三角形优选关系式的“三字经口诀”
拓展提升(例1)
例1.如图,在正方形网格中,圆与网格线相切于格点处,其余的条件见图,根据图示求出∠1的度数.(结果保留小数点后一位.)
分析:要直接求∠1的度的正弦值比较困难,但可以通过“同弧或等弧所对的圆周角相等”进行转化,在把问题化归在网格构成的直角三角形中,用解直角三角形的思路来解决问题.
略解:
设网格中每个小正方形的边长为单位1,则AC=3,BC=1.
在Rt △ACB中,根据勾股定理有:
还有其它途径求∠1的度数吗?
拓展提升(例2)
分析:求DC的长可以化归在Rt△DCB中,根据题中条件需求出一边长才能解决问题;过D点作△ABD的边AB的垂线段,通过直角三角形的边角关系可以求出BD,问题便解决了.
略解:
过D作DE ⊥ AB于E.
∴ ∠AED = ∠BED = 90 °
∵∠A = 30°,AD=4
∵∠ADE = 90°-30°=60°,且∠ADB=105°
∴ ∠EDB = 105°- 60 °=45°
∵在Rt△DCB中有
∴ ∠BDC= 60 °
∴ ∠DBC= 30 °
拓展提升(例3)
分析:本题通过第一个方程可以求出∠A的正弦值,通过第二个方程可以求出直角三角形斜边c的长度;结合∠A的正弦值可以求出a边的值,再利用勾股定理b边的值.
略解:
由第一个方程结合题意可得:
整理配方为:
解得:
由第二个方程结合题意可得:
解得:
(不合题意,舍去)
根据题意和前面的解答画出示意图.
∵∠C = 90°
课外选练
课外选练不提供参考解答!
谈谈收获!
1. 如图,在Rt △ACB中, ∠C=90 °; ∠A、∠B、∠C所对的边分别为a、b、c.
⑴.三边之间的关系:
(勾股定理)
⑵.两锐角之间的关系:
(直角三角形两锐角互余)
⑶.边角之间的关系:
利用上面这些关系,可以“知二求三”(直角除外,已知中至少要有一条边).
2. 解直角三角形基本类型
⑴. 已知两边: ①.已知两直角边; ②.已知一直角边和斜边.
⑵. 已知一角一边: ①.已知一锐角和一直角边; ②.已知一锐角和斜边.
解答时请注意“有斜用弦,无斜用切”.
1.书上28.2.74页练习题,28.2.79页习题2、5题;
2.《锐角三角函数》训练题余弦正切函数部分选做.
作业布置
书面作业:
再
见
!
课外探究:
《课外选练》1、2、3、4题.
