人教版八年级上《13.2画轴对称图形》同步测试(含答案解析)
文档属性
| 名称 | 人教版八年级上《13.2画轴对称图形》同步测试(含答案解析) |  | |
| 格式 | zip | ||
| 文件大小 | 321.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-01-20 19:56:08 | ||
图片预览

文档简介
13.2 画轴对称图形
基础闯关全练
拓展训练
1.(2016山东济宁邹城一模)若点A(a-2,3)和点B(-1,b+5)关于y轴对称,则点C(a,b)在( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
2.在平面直角坐标系内,已知在y轴与直线x=3之间有一点M(a,3),如果该点关于直线x=3的对称点N的坐标为(5,3),那么a的值为( )
A.4 B.3 C.2 D.1
3.如图,在10×10的正方形网格中有一个四边形和两个三角形(所有顶点都在方格的格点上).
(1)请你画出以上三个图形关于直线MN对称的图形;
(2)将(1)中画出的图形与原图形看成一个整体图形,请写出这个整体图形对称轴的条数.
/
能力提升全练
拓展训练
1.(2016江西中考模拟)如图,在3×3的正方形网格中有四个格点A,B,C,D,以其中一点为原点,网格线所在直线为坐标轴,建立平面直角坐标系,使其余三个点中存在两个点关于一条坐标轴对称,则原点是( )
/
A.A点 B.B点 C.C点 D.D点
2.在平面直角坐标系中,已知点P(a,5)在第二象限,则点P关于直线m(直线m上各点的横坐标都是2)对称的点的坐标是( )
A.(-a,5) B.(a,-5)
C.(-a+2,5) D.(-a+4,5)
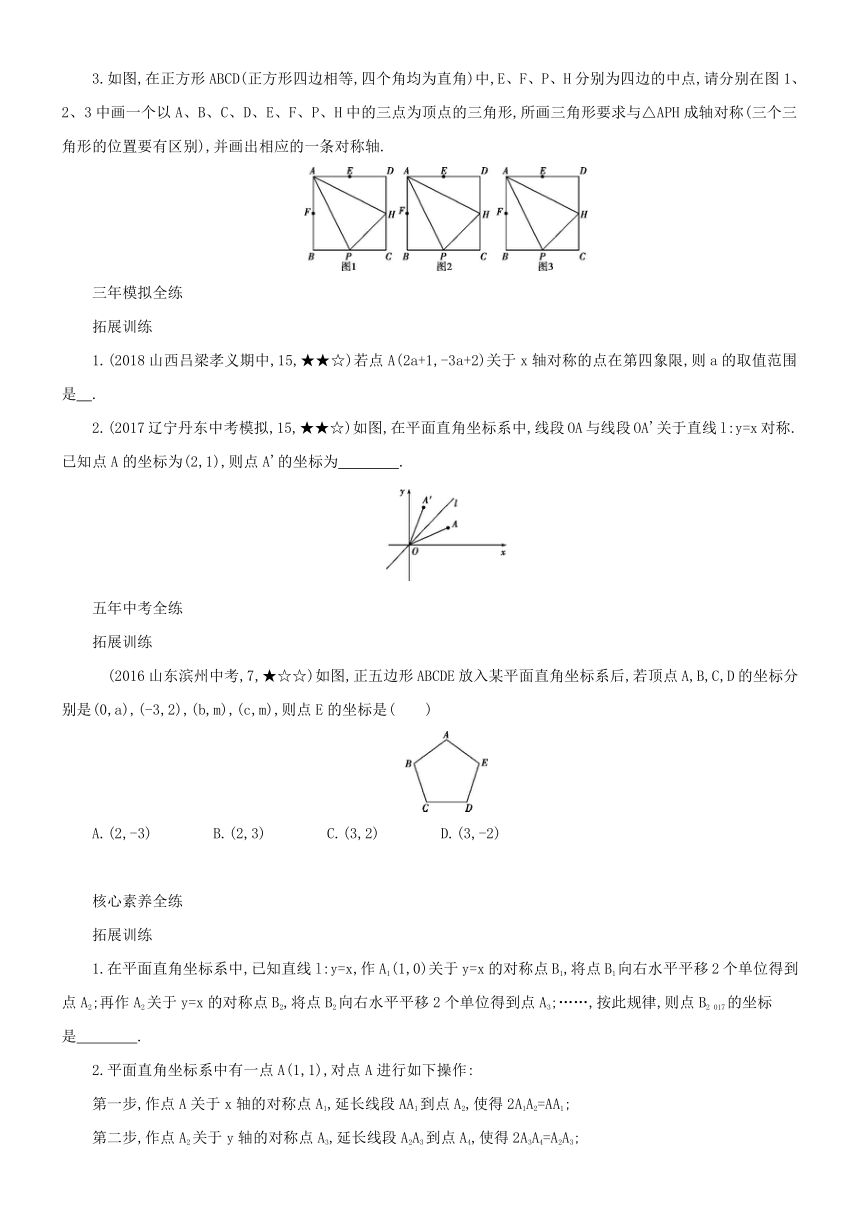
3.如图,在正方形ABCD(正方形四边相等,四个角均为直角)中,E、F、P、H分别为四边的中点,请分别在图1、2、3中画一个以A、B、C、D、E、F、P、H中的三点为顶点的三角形,所画三角形要求与△APH成轴对称(三个三角形的位置要有区别),并画出相应的一条对称轴.
/
三年模拟全练
拓展训练
1.(2018山西吕梁孝义期中,15,★★☆)若点A(2a+1,-3a+2)关于x轴对称的点在第四象限,则a的取值范围是 .?
2.(2017辽宁丹东中考模拟,15,★★☆)如图,在平面直角坐标系中,线段OA与线段OA'关于直线l:y=x对称.已知点A的坐标为(2,1),则点A'的坐标为 .?
/
五年中考全练
拓展训练
(2016山东滨州中考,7,★☆☆)如图,正五边形ABCDE放入某平面直角坐标系后,若顶点A,B,C,D的坐标分别是(0,a),(-3,2),(b,m),(c,m),则点E的坐标是( )
/
A.(2,-3) B.(2,3) C.(3,2) D.(3,-2)
核心素养全练
拓展训练
1.在平面直角坐标系中,已知直线l:y=x,作A1(1,0)关于y=x的对称点B1,将点B1向右水平平移2个单位得到点A2;再作A2关于y=x的对称点B2,将点B2向右水平平移2个单位得到点A3;……,按此规律,则点B2 017的坐标是 .?
2.平面直角坐标系中有一点A(1,1),对点A进行如下操作:
第一步,作点A关于x轴的对称点A1,延长线段AA1到点A2,使得2A1A2=AA1;
第二步,作点A2关于y轴的对称点A3,延长线段A2A3到点A4,使得2A3A4=A2A3;
第三步,作点A4关于x轴的对称点A5,延长线段A4A5到点A6,使得2A5A6=A4A5;
……
则点A2的坐标为 ,点A2 017的坐标为 .?
若点An的坐标恰好为(4m,4n)(m、n均为正整数),请写出m和n的关系式 .?
13.2 画轴对称图形
基础闯关全练
拓展训练
1.D 由点A(a-2,3)和点B(-1,b+5)关于y轴对称,得a-2=1,b+5=3,解得a=3,b=-2,则点C(a,b)在第四象限.
2.D ∵点M关于直线x=3的对称点N的坐标为(5,3),∴点N到直线x=3的距离为2,∴点M(a,3)到直线x=3的距离为2,又点M在y轴与直线x=3之间,∴a=1.
3.解析 (1)所画图形如图所示:
/
(2)这个整体图形共有4条对称轴.
能力提升全练
拓展训练
1.B 如图所示,以B点为原点,建立平面直角坐标系,此时存在两个点A,C关于y轴对称,故选B.
/
2.D ∵直线m上各点的横坐标都是2,点P(a,5)在第二象限,∴点P到直线m的距离为2-a,∴点P关于直线m对称的点的横坐标是2-a+2=4-a,故点P关于直线m对称的点的坐标是(-a+4,5).
3.解析 如图所示(虚线为相应的对称轴):
/
三年模拟全练
拓展训练
1.答案 -
1
2
2
3
解析 ∵点A(2a+1,-3a+2)关于x轴对称的点在第四象限,∴点A在第一象限,∴
2??+1>0①,
-3??+2>0②,
解不等式①得,a>-
1
2
,解不等式②得,a<
2
3
,所以,a的取值范围是-
1
2
2
3
.故答案为-
1
2
2
3
.
2.答案 (1,2)
解析 过点A作AC⊥x轴于点C,过点A'作A'C'⊥y轴于点C',连接AA',则∠ACO=∠A'C'O=90°.
∵线段OA与线段OA'关于直线l:y=x对称,
∴△ODA'≌△ODA,∠C'OD=∠DOC,
∴∠A'OD=∠AOD,OA'=OA,
∴∠C'OD-∠A'OD=∠DOC-∠AOD,即∠A'OC'=∠AOC.
在△ACO和△A'C'O中,
∠??????=∠??'????',
∠??????=∠??'??'??,
????=??'??,
∴△ACO≌△A'C'O,
∴AC=A'C',CO=OC',
∵点A的坐标为(2,1),
∴OC=2,AC=1,∴OC'=2,A'C=1,
∴点A'的坐标为(1,2).
/
五年中考全练
拓展训练
C 由A(0,a)可知点A一定在y轴上,由C(b,m),D(c,m)可知点C与点D关于y轴对称,∴y轴过点A,且垂直平分CD,x轴平行于CD,∴点B与点E关于y轴对称,∵点B(-3,2),∴点E(3,2),故选C.
核心素养全练
拓展训练
1.答案 (2 016,2 017)
解析 如图所示.易知B1(0,1),B2(1,2),B3(2,3),B4(3,4),B5(4,5),依次类推,点B2 017的坐标是(2 016,2 017).
/
2.答案 (1,-2);(2504,-2504);m=n
解析 由题意得,A1(1,-1),A2(1,-2),A3(-1,-2),
A4(-2,-2),A5(-2,2),A6(-2,4),A7(2,4),A8(4,4),
∵2 017÷8=252……1,
∴点A2 017为第253循环组的第一个点,
易知A2 017和A1所在象限一样,A2 017(2504,-2504).
若点An的坐标恰好为(4m,4n)(m、n均为正整数),则m和n的关系式为m=n.
基础闯关全练
拓展训练
1.(2016山东济宁邹城一模)若点A(a-2,3)和点B(-1,b+5)关于y轴对称,则点C(a,b)在( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
2.在平面直角坐标系内,已知在y轴与直线x=3之间有一点M(a,3),如果该点关于直线x=3的对称点N的坐标为(5,3),那么a的值为( )
A.4 B.3 C.2 D.1
3.如图,在10×10的正方形网格中有一个四边形和两个三角形(所有顶点都在方格的格点上).
(1)请你画出以上三个图形关于直线MN对称的图形;
(2)将(1)中画出的图形与原图形看成一个整体图形,请写出这个整体图形对称轴的条数.
/
能力提升全练
拓展训练
1.(2016江西中考模拟)如图,在3×3的正方形网格中有四个格点A,B,C,D,以其中一点为原点,网格线所在直线为坐标轴,建立平面直角坐标系,使其余三个点中存在两个点关于一条坐标轴对称,则原点是( )
/
A.A点 B.B点 C.C点 D.D点
2.在平面直角坐标系中,已知点P(a,5)在第二象限,则点P关于直线m(直线m上各点的横坐标都是2)对称的点的坐标是( )
A.(-a,5) B.(a,-5)
C.(-a+2,5) D.(-a+4,5)
3.如图,在正方形ABCD(正方形四边相等,四个角均为直角)中,E、F、P、H分别为四边的中点,请分别在图1、2、3中画一个以A、B、C、D、E、F、P、H中的三点为顶点的三角形,所画三角形要求与△APH成轴对称(三个三角形的位置要有区别),并画出相应的一条对称轴.
/
三年模拟全练
拓展训练
1.(2018山西吕梁孝义期中,15,★★☆)若点A(2a+1,-3a+2)关于x轴对称的点在第四象限,则a的取值范围是 .?
2.(2017辽宁丹东中考模拟,15,★★☆)如图,在平面直角坐标系中,线段OA与线段OA'关于直线l:y=x对称.已知点A的坐标为(2,1),则点A'的坐标为 .?
/
五年中考全练
拓展训练
(2016山东滨州中考,7,★☆☆)如图,正五边形ABCDE放入某平面直角坐标系后,若顶点A,B,C,D的坐标分别是(0,a),(-3,2),(b,m),(c,m),则点E的坐标是( )
/
A.(2,-3) B.(2,3) C.(3,2) D.(3,-2)
核心素养全练
拓展训练
1.在平面直角坐标系中,已知直线l:y=x,作A1(1,0)关于y=x的对称点B1,将点B1向右水平平移2个单位得到点A2;再作A2关于y=x的对称点B2,将点B2向右水平平移2个单位得到点A3;……,按此规律,则点B2 017的坐标是 .?
2.平面直角坐标系中有一点A(1,1),对点A进行如下操作:
第一步,作点A关于x轴的对称点A1,延长线段AA1到点A2,使得2A1A2=AA1;
第二步,作点A2关于y轴的对称点A3,延长线段A2A3到点A4,使得2A3A4=A2A3;
第三步,作点A4关于x轴的对称点A5,延长线段A4A5到点A6,使得2A5A6=A4A5;
……
则点A2的坐标为 ,点A2 017的坐标为 .?
若点An的坐标恰好为(4m,4n)(m、n均为正整数),请写出m和n的关系式 .?
13.2 画轴对称图形
基础闯关全练
拓展训练
1.D 由点A(a-2,3)和点B(-1,b+5)关于y轴对称,得a-2=1,b+5=3,解得a=3,b=-2,则点C(a,b)在第四象限.
2.D ∵点M关于直线x=3的对称点N的坐标为(5,3),∴点N到直线x=3的距离为2,∴点M(a,3)到直线x=3的距离为2,又点M在y轴与直线x=3之间,∴a=1.
3.解析 (1)所画图形如图所示:
/
(2)这个整体图形共有4条对称轴.
能力提升全练
拓展训练
1.B 如图所示,以B点为原点,建立平面直角坐标系,此时存在两个点A,C关于y轴对称,故选B.
/
2.D ∵直线m上各点的横坐标都是2,点P(a,5)在第二象限,∴点P到直线m的距离为2-a,∴点P关于直线m对称的点的横坐标是2-a+2=4-a,故点P关于直线m对称的点的坐标是(-a+4,5).
3.解析 如图所示(虚线为相应的对称轴):
/
三年模拟全练
拓展训练
1.答案 -
1
2
3
解析 ∵点A(2a+1,-3a+2)关于x轴对称的点在第四象限,∴点A在第一象限,∴
2??+1>0①,
-3??+2>0②,
解不等式①得,a>-
1
2
,解不等式②得,a<
2
3
,所以,a的取值范围是-
1
2
3
.故答案为-
1
2
3
.
2.答案 (1,2)
解析 过点A作AC⊥x轴于点C,过点A'作A'C'⊥y轴于点C',连接AA',则∠ACO=∠A'C'O=90°.
∵线段OA与线段OA'关于直线l:y=x对称,
∴△ODA'≌△ODA,∠C'OD=∠DOC,
∴∠A'OD=∠AOD,OA'=OA,
∴∠C'OD-∠A'OD=∠DOC-∠AOD,即∠A'OC'=∠AOC.
在△ACO和△A'C'O中,
∠??????=∠??'????',
∠??????=∠??'??'??,
????=??'??,
∴△ACO≌△A'C'O,
∴AC=A'C',CO=OC',
∵点A的坐标为(2,1),
∴OC=2,AC=1,∴OC'=2,A'C=1,
∴点A'的坐标为(1,2).
/
五年中考全练
拓展训练
C 由A(0,a)可知点A一定在y轴上,由C(b,m),D(c,m)可知点C与点D关于y轴对称,∴y轴过点A,且垂直平分CD,x轴平行于CD,∴点B与点E关于y轴对称,∵点B(-3,2),∴点E(3,2),故选C.
核心素养全练
拓展训练
1.答案 (2 016,2 017)
解析 如图所示.易知B1(0,1),B2(1,2),B3(2,3),B4(3,4),B5(4,5),依次类推,点B2 017的坐标是(2 016,2 017).
/
2.答案 (1,-2);(2504,-2504);m=n
解析 由题意得,A1(1,-1),A2(1,-2),A3(-1,-2),
A4(-2,-2),A5(-2,2),A6(-2,4),A7(2,4),A8(4,4),
∵2 017÷8=252……1,
∴点A2 017为第253循环组的第一个点,
易知A2 017和A1所在象限一样,A2 017(2504,-2504).
若点An的坐标恰好为(4m,4n)(m、n均为正整数),则m和n的关系式为m=n.
