北师大九年级数学下册1.1锐角三角函数同步训练(附答案)
文档属性
| 名称 | 北师大九年级数学下册1.1锐角三角函数同步训练(附答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 90.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-01-21 09:42:16 | ||
图片预览


文档简介
北师大九年级数学下册 1.1 锐角三角函数 同步训练
学校:__________ 班级:__________ 姓名:__________ 考号:__________
一、 选择题 (本题共计 8 小题 ,每题 3 分 ,共计24分 , )
1. 如图,的三个顶点都在方格纸的格点上,则
A. B. C. D.
?2. 若为锐角,且,则
A.小于 B.大于
C.大于且小于 D.大于
?3. 若,则下列说法不正确的是( )
A.随的增大而增大 B.随的增大而减小
C.随的增大而增大 D.、、的值都随的增大而增大
?4. 如果在中,,,,那么下列各式正确的是( )
A. B.
C. D.
?5. 若把一个直角三角形的两条直角边都扩大倍,(是大于的自然数),则两个锐角的三角函数值( )
A.都变大为原来的倍 B.都缩小为原来的
C.不变化 D.各个函数值变化不一致
?6. 比较,,的大小关系是( )
A. B.
C. D.
?7. 如图,在中,,,的平分线与的外角平分线交于,连接,则的值是( )
A. B. C. D.
?8. 如图,在中,点在上,,垂足为,若,,则等于( )
A. B. C. D.
二、 填空题 (本题共计 8 小题 ,每题 3 分 ,共计24分 , )?
9. ________?(填大小关系)
?10. 在中,,如果,,那么________.
?11. 在中,,当已知和时,求,则、、关系式是________.
?12. 已知在中,为直角,,,________. ?
13. 已知为锐角,且,那么的范围是________.
?14. 在中,,、、分别是、、的对边,下列式子:①,②,③,④,必定成立的是________.
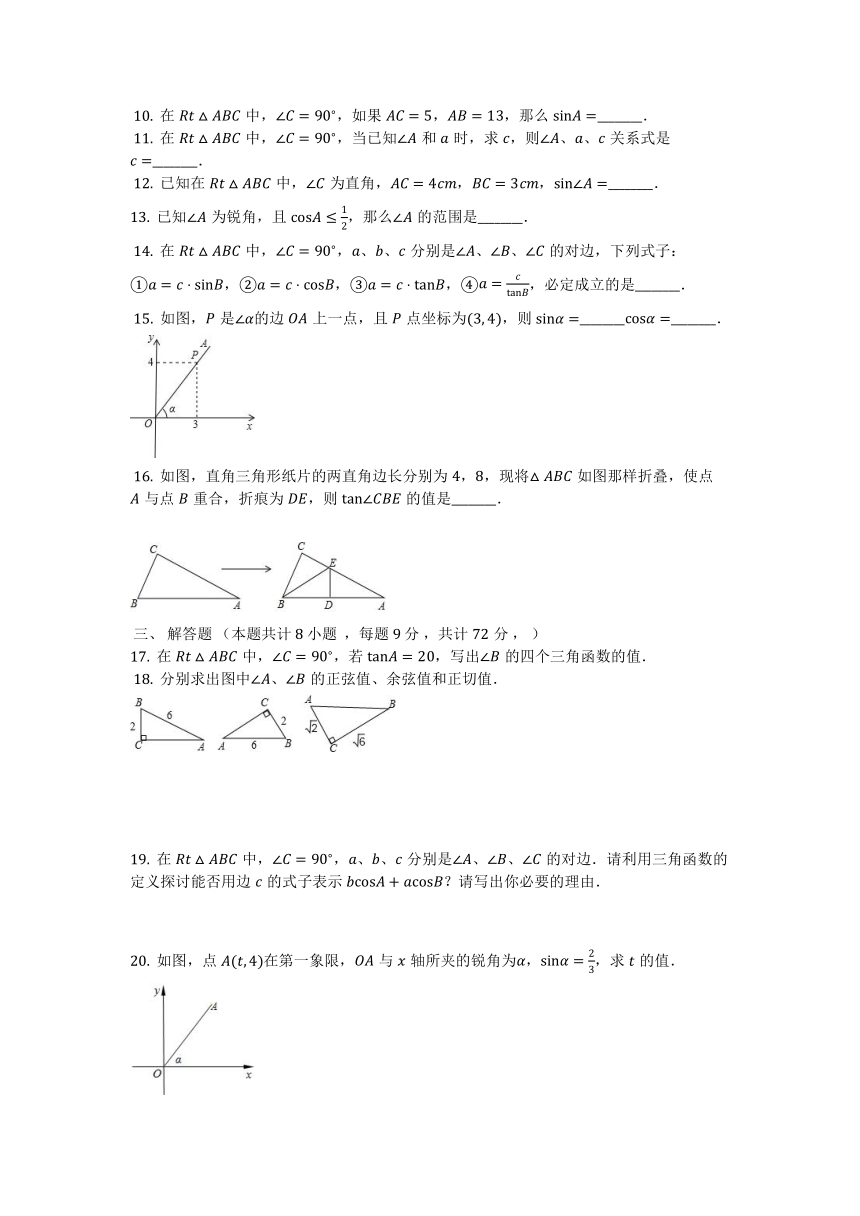
?15. 如图,是的边上一点,且点坐标为,则________________.
?16. 如图,直角三角形纸片的两直角边长分别为,,现将如图那样折叠,使点与点重合,折痕为,则的值是________.
三、 解答题 (本题共计 8 小题 ,每题 9 分 ,共计72分 , )
17. 在中,,若,写出的四个三角函数的值.
?18. 分别求出图中、的正弦值、余弦值和正切值.
19. 在中,,、、分别是、、的对边.请利用三角函数的定义探讨能否用边的式子表示?请写出你必要的理由. ?
20. 如图,点在第一象限,与轴所夹的锐角为,,求的值.
?21. 在中,,,,求的值.
?22. 如图,在中,,是直角边上一点,于点,,,求的值.
?
23. 如图,在中,,,.
求的长;
利用此图形求的值(精确到,参考数据:,,)
?
24. 如图,在四边形中,平分,,,求的值.
答案
1. D
2. D
3. D
4. A
5. C
6. D
7. D
8. D
9.
10.
11.
12.
13.
14. ②
15.
16.
17. 解:,,
由勾股定理,得
,
,
,
.
18. 解:如图,,
,
,
,
,
,
.
如图,,
,
,
,
,
,
.
如图,,
,
,
,
,
,
.
19. 解:∵,,
∴,
即.
20. 解:过作轴于.
∴,
∵,
∴,
∵,
∴,
∴,
∴.
21. 解:在中,,,,
∵,
∴,
则.
22. 解:∵,,
∴,
又∵,
∴,
∴,
设,,
由勾股定理得:,
在中,.
23. 解:过作,交的延长线于点,如图所示:
在中,,
∵,
∴,
∴,
,
在中,,
∴,
∴;
在边上取一点,使得,连接,如图所示:
∵,
∴,
.
24. 解:∵平分,∴.
又∵,
∴.
∴,
在中,∵,
∴.
学校:__________ 班级:__________ 姓名:__________ 考号:__________
一、 选择题 (本题共计 8 小题 ,每题 3 分 ,共计24分 , )
1. 如图,的三个顶点都在方格纸的格点上,则
A. B. C. D.
?2. 若为锐角,且,则
A.小于 B.大于
C.大于且小于 D.大于
?3. 若,则下列说法不正确的是( )
A.随的增大而增大 B.随的增大而减小
C.随的增大而增大 D.、、的值都随的增大而增大
?4. 如果在中,,,,那么下列各式正确的是( )
A. B.
C. D.
?5. 若把一个直角三角形的两条直角边都扩大倍,(是大于的自然数),则两个锐角的三角函数值( )
A.都变大为原来的倍 B.都缩小为原来的
C.不变化 D.各个函数值变化不一致
?6. 比较,,的大小关系是( )
A. B.
C. D.
?7. 如图,在中,,,的平分线与的外角平分线交于,连接,则的值是( )
A. B. C. D.
?8. 如图,在中,点在上,,垂足为,若,,则等于( )
A. B. C. D.
二、 填空题 (本题共计 8 小题 ,每题 3 分 ,共计24分 , )?
9. ________?(填大小关系)
?10. 在中,,如果,,那么________.
?11. 在中,,当已知和时,求,则、、关系式是________.
?12. 已知在中,为直角,,,________. ?
13. 已知为锐角,且,那么的范围是________.
?14. 在中,,、、分别是、、的对边,下列式子:①,②,③,④,必定成立的是________.
?15. 如图,是的边上一点,且点坐标为,则________________.
?16. 如图,直角三角形纸片的两直角边长分别为,,现将如图那样折叠,使点与点重合,折痕为,则的值是________.
三、 解答题 (本题共计 8 小题 ,每题 9 分 ,共计72分 , )
17. 在中,,若,写出的四个三角函数的值.
?18. 分别求出图中、的正弦值、余弦值和正切值.
19. 在中,,、、分别是、、的对边.请利用三角函数的定义探讨能否用边的式子表示?请写出你必要的理由. ?
20. 如图,点在第一象限,与轴所夹的锐角为,,求的值.
?21. 在中,,,,求的值.
?22. 如图,在中,,是直角边上一点,于点,,,求的值.
?
23. 如图,在中,,,.
求的长;
利用此图形求的值(精确到,参考数据:,,)
?
24. 如图,在四边形中,平分,,,求的值.
答案
1. D
2. D
3. D
4. A
5. C
6. D
7. D
8. D
9.
10.
11.
12.
13.
14. ②
15.
16.
17. 解:,,
由勾股定理,得
,
,
,
.
18. 解:如图,,
,
,
,
,
,
.
如图,,
,
,
,
,
,
.
如图,,
,
,
,
,
,
.
19. 解:∵,,
∴,
即.
20. 解:过作轴于.
∴,
∵,
∴,
∵,
∴,
∴,
∴.
21. 解:在中,,,,
∵,
∴,
则.
22. 解:∵,,
∴,
又∵,
∴,
∴,
设,,
由勾股定理得:,
在中,.
23. 解:过作,交的延长线于点,如图所示:
在中,,
∵,
∴,
∴,
,
在中,,
∴,
∴;
在边上取一点,使得,连接,如图所示:
∵,
∴,
.
24. 解:∵平分,∴.
又∵,
∴.
∴,
在中,∵,
∴.
