北师大九年级数学下册第一章直角三角形的边角关系1.4三角函数的应用同步训练(附答案)
文档属性
| 名称 | 北师大九年级数学下册第一章直角三角形的边角关系1.4三角函数的应用同步训练(附答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 138.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-01-21 00:00:00 | ||
图片预览

文档简介
北师大九年级数学下册 第一章 直角三角形的边角关系
1.4 三角函数的应用 同步训练
学校:__________ 班级:__________ 姓名:__________ 考号:__________
一、 选择题 (本题共计 10 小题 ,每题 3 分 ,共计30分 , )?
1. 如图,小明为测量学校旗杆的高度,在操场上选了一点,测得点到旗杆底端的水平距离为米,度,则旗杆的高度为( )
A.米 B.米 C.米 D.米
?2. 工地上有甲、乙二块铁板,铁板甲形状为等腰三角形,其顶角为,腰长为;铁板乙形状为直角梯形,两底边长分别为、,且有一内角为.现在我们把它们任意翻转,分别试图从一个直径为的圆洞中穿过,结果是( )
A.甲板能穿过,乙板不能穿过 B.甲板不能穿过,乙板能穿过
C.甲、乙两板都能穿过 D.甲、乙两板都不能穿过
?3. 如图,斜坡长米,其水平宽度长为米,则斜坡的坡度为( )
A. B. C. D.
?4. 某飞机于空中处探测到地面目标,此时从飞机上看目标的俯角,并测得飞机距离地面目标的距离为米,则此时飞机高度为( )
A.米 B.米
C.米 D.米
?5. 从高的测量仪上,测得某建筑物顶端仰角为,测量仪距建筑物,则建筑物的高大约为( )
A. B. C. D.
?6. 如图所示,是平面镜,光线从点出发经上的点反射后到达点,若入射角为,,,垂足分别为,,且,,,则的值是( )
A. B. C. D.
?7. 如图,某学校数学课外活动小组的同学们,为了测量一个小湖泊两岸的两棵树和之间的距离,在垂直的方向上确定点,如果测得米,,那么和之间的距离是( )米.
A. B.
C. D.
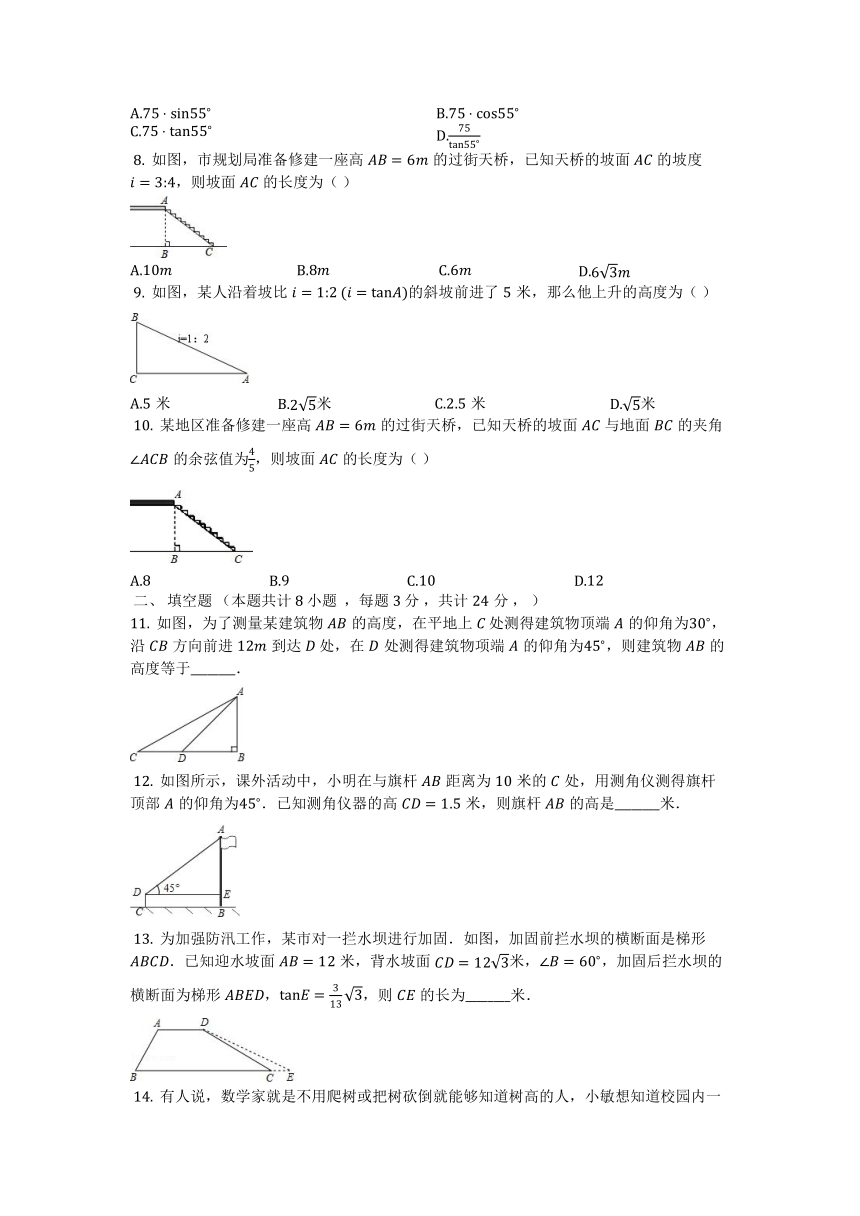
?8. 如图,市规划局准备修建一座高的过街天桥,已知天桥的坡面的坡度,则坡面的长度为( )
A. B. C. D.
?9. 如图,某人沿着坡比?的斜坡前进了米,那么他上升的高度为( )
A.米 B.米 C.米 D.米
?10. 某地区准备修建一座高的过街天桥,已知天桥的坡面与地面的夹角的余弦值为,则坡面的长度为( )
A. B. C. D.
二、 填空题 (本题共计 8 小题 ,每题 3 分 ,共计24分 , )
11. 如图,为了测量某建筑物的高度,在平地上?处测得建筑物顶端的仰角为,沿方向前进到达?处,在处测得建筑物项端的仰角为,则建筑物的高度等于________.
?12. 如图所示,课外活动中,小明在与旗杆距离为米的处,用测角仪测得旗杆顶部的仰角为.已知测角仪器的高米,则旗杆的高是________米.
?13. 为加强防汛工作,某市对一拦水坝进行加固.如图,加固前拦水坝的横断面是梯形.已知迎水坡面米,背水坡面米,,加固后拦水坝的横断面为梯形,,则的长为________米.
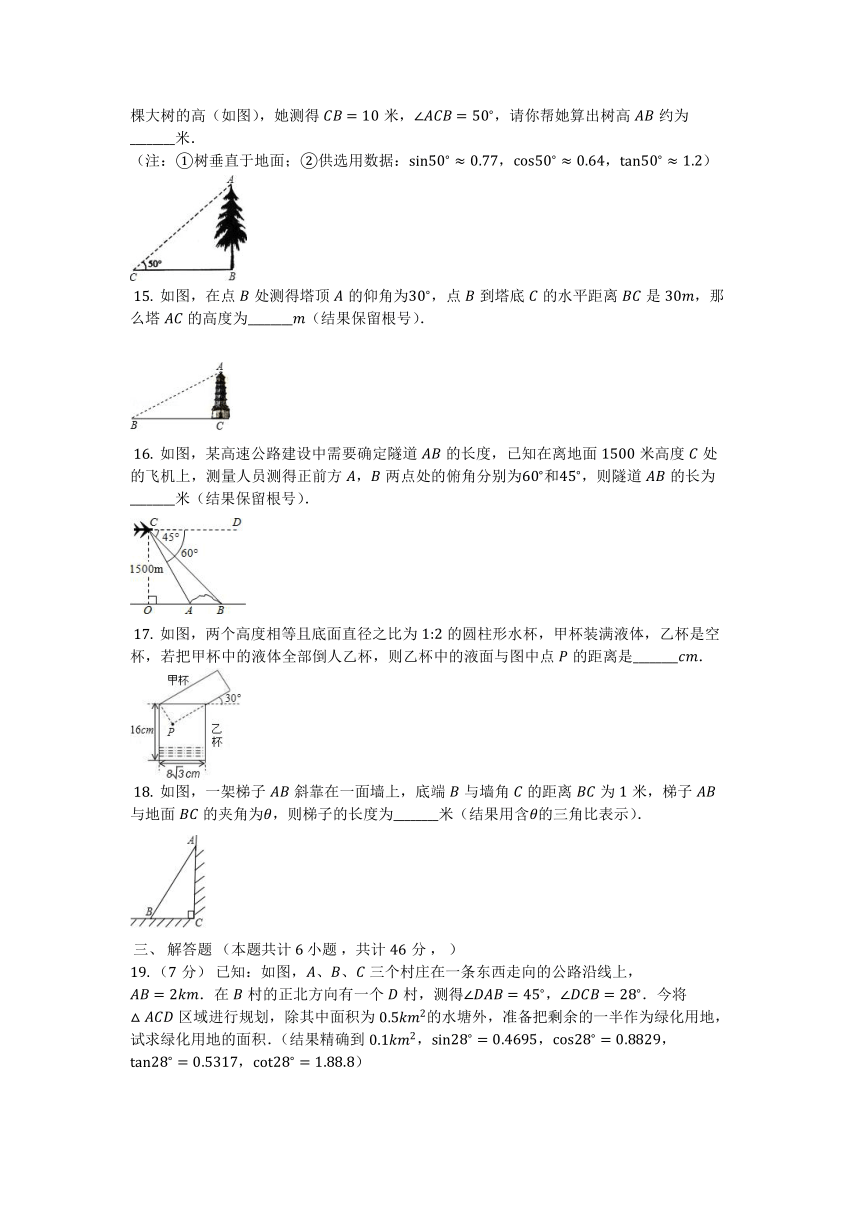
?14. 有人说,数学家就是不用爬树或把树砍倒就能够知道树高的人,小敏想知道校园内一棵大树的高(如图),她测得米,,请你帮她算出树高约为________米.
(注:①树垂直于地面;②供选用数据:,,)
?15. 如图,在点处测得塔顶的仰角为,点到塔底的水平距离是,那么塔的高度为________(结果保留根号).
?16. 如图,某高速公路建设中需要确定隧道的长度,已知在离地面米高度处的飞机上,测量人员测得正前方,两点处的俯角分别为和,则隧道的长为________米(结果保留根号).
?17. 如图,两个高度相等且底面直径之比为的圆柱形水杯,甲杯装满液体,乙杯是空杯,若把甲杯中的液体全部倒人乙杯,则乙杯中的液面与图中点的距离是________.
?18. 如图,一架梯子斜靠在一面墙上,底端与墙角的距离为米,梯子与地面的夹角为,则梯子的长度为________米(结果用含的三角比表示).
三、 解答题 (本题共计 6 小题 ,共计46分 , )
19. (7分) 已知:如图,、、三个村庄在一条东西走向的公路沿线上,.在村的正北方向有一个村,测得,.今将区域进行规划,除其中面积为的水塘外,准备把剩余的一半作为绿化用地,试求绿化用地的面积.(结果精确到,,,,)
?
20. (7分) 如图,某游乐场内有一观光塔,在塔顶处进行观测,测得山坡上点处的俯角为,山脚点处的俯角为,已知该山坡的坡度为(即),且、、在同一直线上.若山坡上点到山脚点的距离为米,求观光塔的高度.
?
21. (8分) 如图,山上有一根电线杆,山脚下有一矩形建筑物,从、两点测得电线杆顶端的仰角分别为,,该建筑物顶端宽度,高度.计算电线杆顶端到地面的高度(精确到).
(参考数据:,,,)
?
22.(8分) 如图,某仓储中心有一斜坡,其坡度为,顶部处的高为,、在同一水平地面上.
求斜坡的水平宽度;
矩形为长方体货柜的侧面图,其中,,将该货柜沿斜坡向上运送,当时,求点离地面的高.,结果精确到
?
23. (8分) 边防战士在海拔高度为米(即的长)的小岛顶部处执行任务,上午点,发现在海面上的处有一艘船,此时测得该船的俯角为,该船沿着方向航行一段时间后到达处,又测得该船的俯角为,求该船在这一段时间内的航程.
?
24. (8分) 如图,竖直立着的水泥柱子上挂着一个矩形广告牌,已知,且与水平地面垂直,经过测量得到的数据如图所示.其中,,,点、、在一条直线上.视线和交于点,请根据以上数据计算广告牌的高度.(,结果精确到米)
答案
1. D
2. A
3. C
4. D
5. B
6. D
7. C
8. A
9. D
10. C
11.
12.
13.
14.
15.
16.
17.
18.
19. 绿化用地的面积为.
20. 观光塔的高度为米?
21. 电线杆顶端到地面的高度约为.
22. 解:∵坡度为,,
∴.
作,垂足为,且与相交于.
∵,,
∴,
∴,
∵,
∴,
∴,,
设,则,
∴,
∴,
∴.
23. 该船在这一段时间内的航程米.
24. 广告牌的高度是.
1.4 三角函数的应用 同步训练
学校:__________ 班级:__________ 姓名:__________ 考号:__________
一、 选择题 (本题共计 10 小题 ,每题 3 分 ,共计30分 , )?
1. 如图,小明为测量学校旗杆的高度,在操场上选了一点,测得点到旗杆底端的水平距离为米,度,则旗杆的高度为( )
A.米 B.米 C.米 D.米
?2. 工地上有甲、乙二块铁板,铁板甲形状为等腰三角形,其顶角为,腰长为;铁板乙形状为直角梯形,两底边长分别为、,且有一内角为.现在我们把它们任意翻转,分别试图从一个直径为的圆洞中穿过,结果是( )
A.甲板能穿过,乙板不能穿过 B.甲板不能穿过,乙板能穿过
C.甲、乙两板都能穿过 D.甲、乙两板都不能穿过
?3. 如图,斜坡长米,其水平宽度长为米,则斜坡的坡度为( )
A. B. C. D.
?4. 某飞机于空中处探测到地面目标,此时从飞机上看目标的俯角,并测得飞机距离地面目标的距离为米,则此时飞机高度为( )
A.米 B.米
C.米 D.米
?5. 从高的测量仪上,测得某建筑物顶端仰角为,测量仪距建筑物,则建筑物的高大约为( )
A. B. C. D.
?6. 如图所示,是平面镜,光线从点出发经上的点反射后到达点,若入射角为,,,垂足分别为,,且,,,则的值是( )
A. B. C. D.
?7. 如图,某学校数学课外活动小组的同学们,为了测量一个小湖泊两岸的两棵树和之间的距离,在垂直的方向上确定点,如果测得米,,那么和之间的距离是( )米.
A. B.
C. D.
?8. 如图,市规划局准备修建一座高的过街天桥,已知天桥的坡面的坡度,则坡面的长度为( )
A. B. C. D.
?9. 如图,某人沿着坡比?的斜坡前进了米,那么他上升的高度为( )
A.米 B.米 C.米 D.米
?10. 某地区准备修建一座高的过街天桥,已知天桥的坡面与地面的夹角的余弦值为,则坡面的长度为( )
A. B. C. D.
二、 填空题 (本题共计 8 小题 ,每题 3 分 ,共计24分 , )
11. 如图,为了测量某建筑物的高度,在平地上?处测得建筑物顶端的仰角为,沿方向前进到达?处,在处测得建筑物项端的仰角为,则建筑物的高度等于________.
?12. 如图所示,课外活动中,小明在与旗杆距离为米的处,用测角仪测得旗杆顶部的仰角为.已知测角仪器的高米,则旗杆的高是________米.
?13. 为加强防汛工作,某市对一拦水坝进行加固.如图,加固前拦水坝的横断面是梯形.已知迎水坡面米,背水坡面米,,加固后拦水坝的横断面为梯形,,则的长为________米.
?14. 有人说,数学家就是不用爬树或把树砍倒就能够知道树高的人,小敏想知道校园内一棵大树的高(如图),她测得米,,请你帮她算出树高约为________米.
(注:①树垂直于地面;②供选用数据:,,)
?15. 如图,在点处测得塔顶的仰角为,点到塔底的水平距离是,那么塔的高度为________(结果保留根号).
?16. 如图,某高速公路建设中需要确定隧道的长度,已知在离地面米高度处的飞机上,测量人员测得正前方,两点处的俯角分别为和,则隧道的长为________米(结果保留根号).
?17. 如图,两个高度相等且底面直径之比为的圆柱形水杯,甲杯装满液体,乙杯是空杯,若把甲杯中的液体全部倒人乙杯,则乙杯中的液面与图中点的距离是________.
?18. 如图,一架梯子斜靠在一面墙上,底端与墙角的距离为米,梯子与地面的夹角为,则梯子的长度为________米(结果用含的三角比表示).
三、 解答题 (本题共计 6 小题 ,共计46分 , )
19. (7分) 已知:如图,、、三个村庄在一条东西走向的公路沿线上,.在村的正北方向有一个村,测得,.今将区域进行规划,除其中面积为的水塘外,准备把剩余的一半作为绿化用地,试求绿化用地的面积.(结果精确到,,,,)
?
20. (7分) 如图,某游乐场内有一观光塔,在塔顶处进行观测,测得山坡上点处的俯角为,山脚点处的俯角为,已知该山坡的坡度为(即),且、、在同一直线上.若山坡上点到山脚点的距离为米,求观光塔的高度.
?
21. (8分) 如图,山上有一根电线杆,山脚下有一矩形建筑物,从、两点测得电线杆顶端的仰角分别为,,该建筑物顶端宽度,高度.计算电线杆顶端到地面的高度(精确到).
(参考数据:,,,)
?
22.(8分) 如图,某仓储中心有一斜坡,其坡度为,顶部处的高为,、在同一水平地面上.
求斜坡的水平宽度;
矩形为长方体货柜的侧面图,其中,,将该货柜沿斜坡向上运送,当时,求点离地面的高.,结果精确到
?
23. (8分) 边防战士在海拔高度为米(即的长)的小岛顶部处执行任务,上午点,发现在海面上的处有一艘船,此时测得该船的俯角为,该船沿着方向航行一段时间后到达处,又测得该船的俯角为,求该船在这一段时间内的航程.
?
24. (8分) 如图,竖直立着的水泥柱子上挂着一个矩形广告牌,已知,且与水平地面垂直,经过测量得到的数据如图所示.其中,,,点、、在一条直线上.视线和交于点,请根据以上数据计算广告牌的高度.(,结果精确到米)
答案
1. D
2. A
3. C
4. D
5. B
6. D
7. C
8. A
9. D
10. C
11.
12.
13.
14.
15.
16.
17.
18.
19. 绿化用地的面积为.
20. 观光塔的高度为米?
21. 电线杆顶端到地面的高度约为.
22. 解:∵坡度为,,
∴.
作,垂足为,且与相交于.
∵,,
∴,
∴,
∵,
∴,
∴,,
设,则,
∴,
∴,
∴.
23. 该船在这一段时间内的航程米.
24. 广告牌的高度是.
