数学人教A版选修2-1 2.2.1 椭圆及其标准方程 课件(28张)
文档属性
| 名称 | 数学人教A版选修2-1 2.2.1 椭圆及其标准方程 课件(28张) |  | |
| 格式 | zip | ||
| 文件大小 | 863.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-01-22 10:51:07 | ||
图片预览





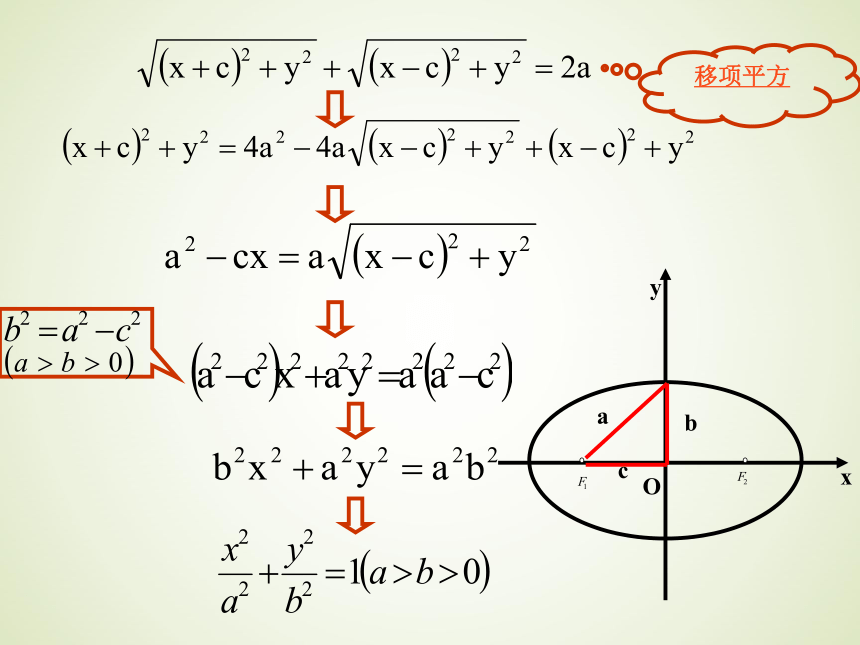
文档简介
课件28张PPT。椭圆及其标准方程F1F2取一长度固定的细绳,两端固定于平面上不同的两点。套上铅笔,拉紧绳子,移动笔尖,画出的轨迹是什么?椭圆是满足什么条件的点的轨迹?给椭圆下一个定义,就是用精确的严密的语言
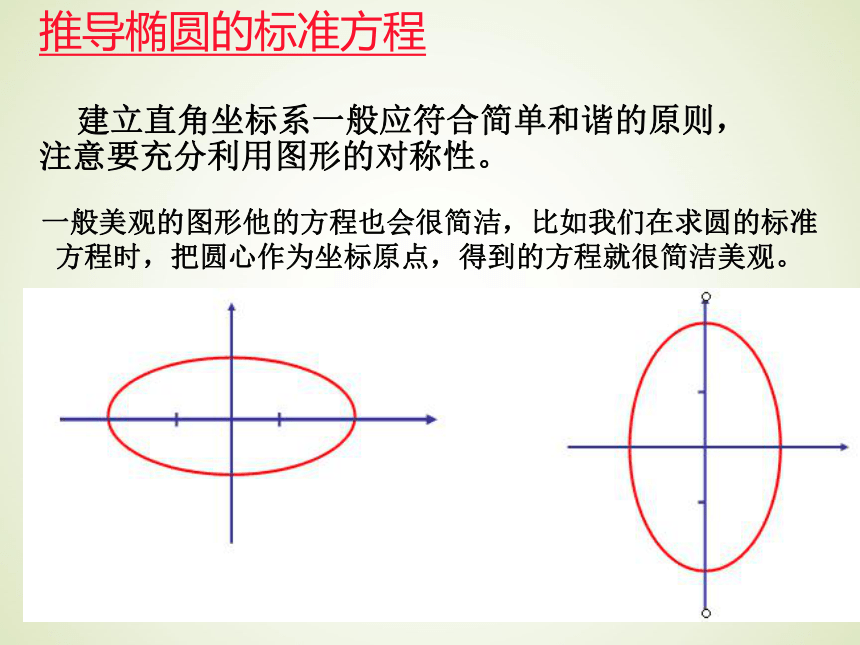
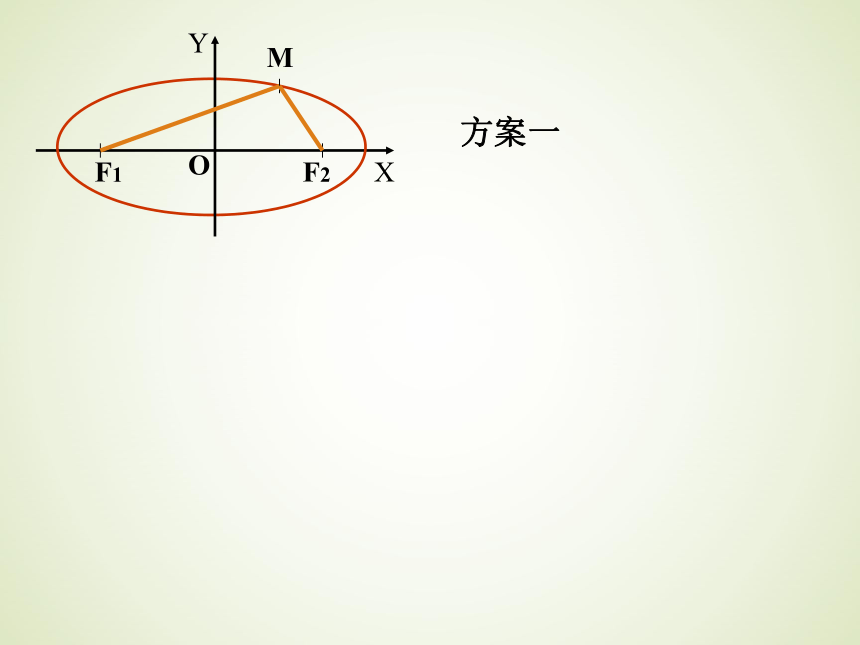
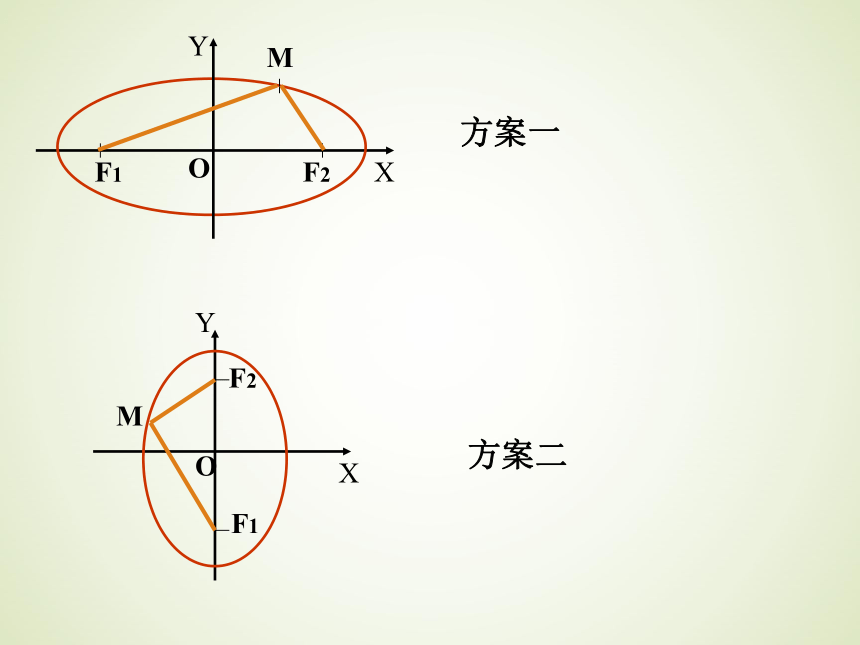
把椭圆的特点描述出来。1、椭圆的定义: 平面内到两个定点F1、F2的距离之和等于常数(大于|F1F2|)的点的轨迹叫做椭圆。 这两个定点叫做椭圆的焦点,两焦点间的距离叫做椭圆的焦距。几点说明:1、F1、F2是两个不同的定点;2、M是椭圆上任意一点,且|MF1| + |MF2| = 常数;3、通常这个常数记为2a,焦距记为2c,且2a>2c(?);4、如果2a = 2c,则M点的轨迹是5、如果2a < 2c,则M点的轨迹 下面我们来求椭圆的标准方程.线段F1F2.不存在.|MF1| + |MF2| = |F1F2| |MF1| + |MF2| < |F1F2| 推导椭圆的标准方程建立椭圆的方程就是要用代数式子椭圆是平面内到两个定点F1、F2的距离之和等于常数(大于|F1F2|)的点的轨迹表示出|MF1| + |MF2| = 常数描绘出椭圆的几何特征推导椭圆的标准方程 建立直角坐标系一般应符合简单和谐的原则,注意要充分利用图形的对称性。一般美观的图形他的方程也会很简洁,比如我们在求圆的标准方程时,把圆心作为坐标原点,得到的方程就很简洁美观。rOXYF1F2M方案一OXYF1F2MOXYF1F2M方案一方案二 以直线F1F2为x轴,线段F1F2的垂直平分线为y轴,建立如图坐标系。设P(x,y)为椭圆上的任意一点,∵F1F2=2c(c>0),则:F1(-c,0)、F2(c,0)∵∴对于含有两个
根式的方程,
可以采用移项
两边平方或者
分子有理化进
行化简。
方程的推导移项平方acbOXYF1F2M(-c,0)(c,0)OXYF1F2M(0,-c)(0 , c)椭圆的标准方程的再认识:(1)椭圆标准方程的形式:(2)椭圆的标准方程中三个参数a、b、c满足(3)椭圆的标准方程中,x2与y2的分母哪一个大,则焦点在
哪一个轴上。能不能不画图,只从标准方程就可以知道焦点在那个坐标轴上?左边是两个分式的平方和,右边是1椭圆的标准方程 定 义图 形方 程焦 点F(±c,0)F(0,±c)a,b,c之间的关系c2=a2-b2|MF1|+|MF2|=2a小 结:注意:(3)若a2在 x2之下,则焦点在x轴上;若a2在y2之下,则焦点在y轴上.
哪个字母下面的分母大,焦点在哪个轴上。(2)a、b、c有关系式:c2=a2-b2,即a2=b2+c2,a最大.(1)在两种方程中,总有a>b>0;例1:1.口答:下列方程哪些表示椭圆? 若是,则判定其焦点在何轴?
并指明 ,写出焦点坐标.[分析] (1)中,根据椭圆方程求出a,利用椭圆定义求点M到另一个焦点的距离.
(2)中,由方程表示椭圆知分母都为正值,由焦点位置确定分母的大小.
[方法规律总结]
1.由椭圆的标准方程可求a、b、c的值,进而可求焦点坐标等.
2.椭圆标准方程中,哪个项的分母大,焦点就在哪个轴上. 求椭圆的标准方程 一、二、二、三一个概念;二个方程;三个意识:求美意识,
求简意识,
猜想的意识。小结二个方法:
把椭圆的特点描述出来。1、椭圆的定义: 平面内到两个定点F1、F2的距离之和等于常数(大于|F1F2|)的点的轨迹叫做椭圆。 这两个定点叫做椭圆的焦点,两焦点间的距离叫做椭圆的焦距。几点说明:1、F1、F2是两个不同的定点;2、M是椭圆上任意一点,且|MF1| + |MF2| = 常数;3、通常这个常数记为2a,焦距记为2c,且2a>2c(?);4、如果2a = 2c,则M点的轨迹是5、如果2a < 2c,则M点的轨迹 下面我们来求椭圆的标准方程.线段F1F2.不存在.|MF1| + |MF2| = |F1F2| |MF1| + |MF2| < |F1F2| 推导椭圆的标准方程建立椭圆的方程就是要用代数式子椭圆是平面内到两个定点F1、F2的距离之和等于常数(大于|F1F2|)的点的轨迹表示出|MF1| + |MF2| = 常数描绘出椭圆的几何特征推导椭圆的标准方程 建立直角坐标系一般应符合简单和谐的原则,注意要充分利用图形的对称性。一般美观的图形他的方程也会很简洁,比如我们在求圆的标准方程时,把圆心作为坐标原点,得到的方程就很简洁美观。rOXYF1F2M方案一OXYF1F2MOXYF1F2M方案一方案二 以直线F1F2为x轴,线段F1F2的垂直平分线为y轴,建立如图坐标系。设P(x,y)为椭圆上的任意一点,∵F1F2=2c(c>0),则:F1(-c,0)、F2(c,0)∵∴对于含有两个
根式的方程,
可以采用移项
两边平方或者
分子有理化进
行化简。
方程的推导移项平方acbOXYF1F2M(-c,0)(c,0)OXYF1F2M(0,-c)(0 , c)椭圆的标准方程的再认识:(1)椭圆标准方程的形式:(2)椭圆的标准方程中三个参数a、b、c满足(3)椭圆的标准方程中,x2与y2的分母哪一个大,则焦点在
哪一个轴上。能不能不画图,只从标准方程就可以知道焦点在那个坐标轴上?左边是两个分式的平方和,右边是1椭圆的标准方程 定 义图 形方 程焦 点F(±c,0)F(0,±c)a,b,c之间的关系c2=a2-b2|MF1|+|MF2|=2a小 结:注意:(3)若a2在 x2之下,则焦点在x轴上;若a2在y2之下,则焦点在y轴上.
哪个字母下面的分母大,焦点在哪个轴上。(2)a、b、c有关系式:c2=a2-b2,即a2=b2+c2,a最大.(1)在两种方程中,总有a>b>0;例1:1.口答:下列方程哪些表示椭圆? 若是,则判定其焦点在何轴?
并指明 ,写出焦点坐标.[分析] (1)中,根据椭圆方程求出a,利用椭圆定义求点M到另一个焦点的距离.
(2)中,由方程表示椭圆知分母都为正值,由焦点位置确定分母的大小.
[方法规律总结]
1.由椭圆的标准方程可求a、b、c的值,进而可求焦点坐标等.
2.椭圆标准方程中,哪个项的分母大,焦点就在哪个轴上. 求椭圆的标准方程 一、二、二、三一个概念;二个方程;三个意识:求美意识,
求简意识,
猜想的意识。小结二个方法:
