人教版九年级数学下册_第26章_反比例函数_26.1_反比例函数_同步测试题(含答案)
文档属性
| 名称 | 人教版九年级数学下册_第26章_反比例函数_26.1_反比例函数_同步测试题(含答案) | 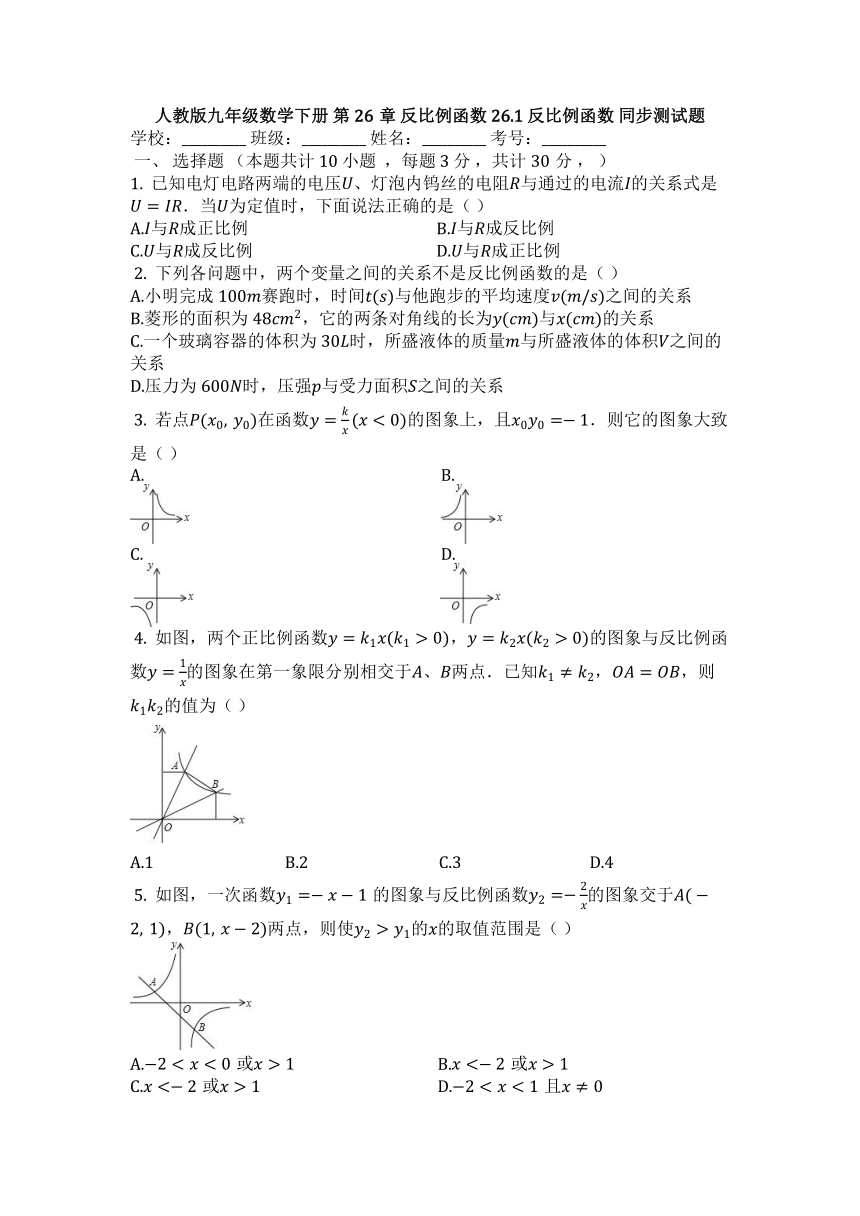 | |
| 格式 | zip | ||
| 文件大小 | 98.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-01-21 20:18:27 | ||
图片预览




文档简介
人教版九年级数学下册 第26章 反比例函数 26.1 反比例函数 同步测试题
学校:__________ 班级:__________ 姓名:__________ 考号:__________
一、 选择题 (本题共计 10 小题 ,每题 3 分 ,共计30分 , )
1. 已知电灯电路两端的电压、灯泡内钨丝的电阻与通过的电流的关系式是.当为定值时,下面说法正确的是( )
A.与成正比例 B.与成反比例
C.与成反比例 D.与成正比例
?2. 下列各问题中,两个变量之间的关系不是反比例函数的是( )
A.小明完成赛跑时,时间与他跑步的平均速度之间的关系
B.菱形的面积为,它的两条对角线的长为与的关系
C.一个玻璃容器的体积为时,所盛液体的质量与所盛液体的体积之间的关系
D.压力为时,压强与受力面积之间的关系
?3. 若点在函数的图象上,且.则它的图象大致是( )
A. B.
C. D.
?4. 如图,两个正比例函数,的图象与反比例函数的图象在第一象限分别相交于、两点.已知,,则的值为( )
A. B. C. D.
?5. 如图,一次函数的图象与反比例函数的图象交于,两点,则使的的取值范围是( )
A.或 B.或
C.或 D.且
?6. 已知正比例函数与反比例函数的图象交于、两点,若点,则点的坐标为( )
A. B. C. D.
?7. 下面说法错误的是( )
A.直线就是一、三象限的角平分线
B.函数的图象经过点
C.函数中随的增大而减小
D.抛物线的对称轴是直线
?8. 已知正比例函数与反比例函数的图象有一个交点的坐标为,则它们的另一个交点的坐标是( )
A.? B.
C. D.
?9. 着点在函数的图象上,且,则它的图象位于( )
A.第一、三象限 B.第二象限
C.第四象限 D.第二、四象限
?10. 若直线与双曲线的一个分支相交,则该分支的图象大致是( )
A. B.
C. D.
二、 填空题 (本题共计 10 小题 ,每题 3 分 ,共计30分 , )
11. 反比例函数的图象经过点,则的值等于________.
?12. 在函数中,自变量的取值范围是________;函数过点,则________.
?13. 反比例函数的图象经过点,则的值为________.
?14. 下列函数中是反比例函数的有________??(填序号).
①;?②;?③;?④;?⑤;?⑥;?⑦为常数,
?15. 如图,在平面直角坐标系中,矩形的对称轴与坐标轴重合,顶点的坐标为.若反比例函数的图象经过点,则的值为________.
?16. 一次函数与反比例函数,在同一直角坐标系中的图象如图所示,若,则的取值范围是________.
?17. 反比例函数图象如图所示,则随的增大而________.
?18. 写一个当时,随的增大而增大的函数解析式________.
?19. 设是反比例函数,则________;其图象经过第________象限;当时,随的增大而________.
?20. 如图,直线与交于、两点,则:
(1)________,________;
当时,的取值范围为________.
三、 解答题 (本题共计 6 小题 ,每题 10 分 ,共计60分 , )
21. 已知函数和函数的图象都经过点?.
求、的值;
求两图象的另一交点.
?22. 已知反比例函数的图象过点.
这个函数的图象分布在哪些象限?随的增大如何变化?
点、、是否在这个函数的图象上.
?
23. 如图是反比例函数的图象的一支.
根据图象画出图象的另一支,并确定常数的取值范围.
若点和点是该反比例函数图象上的两点,请判断、所在象限及与的大小,并说明判断理由.
?
24. 如图,已知反比例函数的图象经过直角三角形斜边的中点,且与直角边相交于点.若点的坐标为.求:
点的坐标;
反比例函数的解析式;
(3)的面积.
?
25. 如图,已知、是一次函数的图象与反比例函数的图象的两个交点.
求、的值;
求一次函数的关系式;
根据图象写出使一次函数的值小于反比例函数的值的的取值范围.
?
26. 如图,一次函数的图象与反比例函数在第一象限的图象交于和两点.
求反比例函数的解析式与点坐标;
求的面积;
在第一象限内,当一次函数的值小于反比例函数的值时,写出自变量的取值范围.
答案
1. B
2. C
3. B
4. A
5. A
6. A
7. C
8. D
9. B
10. B
11.
12.
13.
14. ②③④⑦
15.
16. 或
17. 减小
18. 或或等
19. 一、三减小
20. 或
21. 解:把代入,得,∴
把代入,得
∴;由知,
∴
∴,
∴,
∴两图象的另一交点坐标为.
22. 解:设反比例函数;
把代入得,
即.
∴反比例函数为.函数图象分布在二,四象限,在各自象限内随的增大而增大;把、、的坐标分别代入函数解析式知:
;;;
∴点、在这个函数的图象上.
点不在函数的图象上.
23. 解:如图所示,∵反比例函数的图象的一支在第一象限,
∴,
解得.
∵反比例函数的图象关于原点对称,
∴另一支的图象如图所示:
;点、在第三象限,.理由如下:
∵由知,.
∴,,
∴点和点在第三象限的双曲线上.
∵在第三象限内,随的增大而减小,且,
∴.
24. 解:∵点是斜边的中点,点的坐标为,
∴;把代入,得到
,
故该反比例函数解析式为:;∵,且,
∴.
25. 解:把代入得:,
即反比例函数的解析式为,
把代入得:,
即,
即,;把、的坐标代入一次函数的解析式得:
解得:,,
即一次函数的解析式是;一次函数的值小于反比例函数的值的的取值范围是或.
26. ∵一次函数的图象过点,
∴,解得:,
∴点的坐标为.
∵反比例函数过点,
∴,
∴反比例函数的解析式为.
联立,解得:或,
∴点的坐标为.延长交轴与点,则,如图所示.
∵,,
∴.观察函数图象,发现:
当或时,反比例函数图象在一次函数图象上方,
∴当一次函数的值小于反比例函数的值时,的取值范围为或.
学校:__________ 班级:__________ 姓名:__________ 考号:__________
一、 选择题 (本题共计 10 小题 ,每题 3 分 ,共计30分 , )
1. 已知电灯电路两端的电压、灯泡内钨丝的电阻与通过的电流的关系式是.当为定值时,下面说法正确的是( )
A.与成正比例 B.与成反比例
C.与成反比例 D.与成正比例
?2. 下列各问题中,两个变量之间的关系不是反比例函数的是( )
A.小明完成赛跑时,时间与他跑步的平均速度之间的关系
B.菱形的面积为,它的两条对角线的长为与的关系
C.一个玻璃容器的体积为时,所盛液体的质量与所盛液体的体积之间的关系
D.压力为时,压强与受力面积之间的关系
?3. 若点在函数的图象上,且.则它的图象大致是( )
A. B.
C. D.
?4. 如图,两个正比例函数,的图象与反比例函数的图象在第一象限分别相交于、两点.已知,,则的值为( )
A. B. C. D.
?5. 如图,一次函数的图象与反比例函数的图象交于,两点,则使的的取值范围是( )
A.或 B.或
C.或 D.且
?6. 已知正比例函数与反比例函数的图象交于、两点,若点,则点的坐标为( )
A. B. C. D.
?7. 下面说法错误的是( )
A.直线就是一、三象限的角平分线
B.函数的图象经过点
C.函数中随的增大而减小
D.抛物线的对称轴是直线
?8. 已知正比例函数与反比例函数的图象有一个交点的坐标为,则它们的另一个交点的坐标是( )
A.? B.
C. D.
?9. 着点在函数的图象上,且,则它的图象位于( )
A.第一、三象限 B.第二象限
C.第四象限 D.第二、四象限
?10. 若直线与双曲线的一个分支相交,则该分支的图象大致是( )
A. B.
C. D.
二、 填空题 (本题共计 10 小题 ,每题 3 分 ,共计30分 , )
11. 反比例函数的图象经过点,则的值等于________.
?12. 在函数中,自变量的取值范围是________;函数过点,则________.
?13. 反比例函数的图象经过点,则的值为________.
?14. 下列函数中是反比例函数的有________??(填序号).
①;?②;?③;?④;?⑤;?⑥;?⑦为常数,
?15. 如图,在平面直角坐标系中,矩形的对称轴与坐标轴重合,顶点的坐标为.若反比例函数的图象经过点,则的值为________.
?16. 一次函数与反比例函数,在同一直角坐标系中的图象如图所示,若,则的取值范围是________.
?17. 反比例函数图象如图所示,则随的增大而________.
?18. 写一个当时,随的增大而增大的函数解析式________.
?19. 设是反比例函数,则________;其图象经过第________象限;当时,随的增大而________.
?20. 如图,直线与交于、两点,则:
(1)________,________;
当时,的取值范围为________.
三、 解答题 (本题共计 6 小题 ,每题 10 分 ,共计60分 , )
21. 已知函数和函数的图象都经过点?.
求、的值;
求两图象的另一交点.
?22. 已知反比例函数的图象过点.
这个函数的图象分布在哪些象限?随的增大如何变化?
点、、是否在这个函数的图象上.
?
23. 如图是反比例函数的图象的一支.
根据图象画出图象的另一支,并确定常数的取值范围.
若点和点是该反比例函数图象上的两点,请判断、所在象限及与的大小,并说明判断理由.
?
24. 如图,已知反比例函数的图象经过直角三角形斜边的中点,且与直角边相交于点.若点的坐标为.求:
点的坐标;
反比例函数的解析式;
(3)的面积.
?
25. 如图,已知、是一次函数的图象与反比例函数的图象的两个交点.
求、的值;
求一次函数的关系式;
根据图象写出使一次函数的值小于反比例函数的值的的取值范围.
?
26. 如图,一次函数的图象与反比例函数在第一象限的图象交于和两点.
求反比例函数的解析式与点坐标;
求的面积;
在第一象限内,当一次函数的值小于反比例函数的值时,写出自变量的取值范围.
答案
1. B
2. C
3. B
4. A
5. A
6. A
7. C
8. D
9. B
10. B
11.
12.
13.
14. ②③④⑦
15.
16. 或
17. 减小
18. 或或等
19. 一、三减小
20. 或
21. 解:把代入,得,∴
把代入,得
∴;由知,
∴
∴,
∴,
∴两图象的另一交点坐标为.
22. 解:设反比例函数;
把代入得,
即.
∴反比例函数为.函数图象分布在二,四象限,在各自象限内随的增大而增大;把、、的坐标分别代入函数解析式知:
;;;
∴点、在这个函数的图象上.
点不在函数的图象上.
23. 解:如图所示,∵反比例函数的图象的一支在第一象限,
∴,
解得.
∵反比例函数的图象关于原点对称,
∴另一支的图象如图所示:
;点、在第三象限,.理由如下:
∵由知,.
∴,,
∴点和点在第三象限的双曲线上.
∵在第三象限内,随的增大而减小,且,
∴.
24. 解:∵点是斜边的中点,点的坐标为,
∴;把代入,得到
,
故该反比例函数解析式为:;∵,且,
∴.
25. 解:把代入得:,
即反比例函数的解析式为,
把代入得:,
即,
即,;把、的坐标代入一次函数的解析式得:
解得:,,
即一次函数的解析式是;一次函数的值小于反比例函数的值的的取值范围是或.
26. ∵一次函数的图象过点,
∴,解得:,
∴点的坐标为.
∵反比例函数过点,
∴,
∴反比例函数的解析式为.
联立,解得:或,
∴点的坐标为.延长交轴与点,则,如图所示.
∵,,
∴.观察函数图象,发现:
当或时,反比例函数图象在一次函数图象上方,
∴当一次函数的值小于反比例函数的值时,的取值范围为或.
