苏科版九年级数学下册_第六章_图形的相似_单元检测试卷(含答案)
文档属性
| 名称 | 苏科版九年级数学下册_第六章_图形的相似_单元检测试卷(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 153.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-01-21 00:00:00 | ||
图片预览




文档简介
苏科版九年级数学下册 第六章 图形的相似 单元检测试卷
学校:__________ 班级:__________ 姓名:__________ 考号:__________
一、 选择题 (本题共计 10 小题 ,每题 3 分 ,共计30分 , )
1. 若,则的值为( )
A. B. C. D.
?2. 东海大桥全长千米,如果东海大桥在某张地图上的长为厘米,那么该地图上距离与实际距离的比为( )
A. B.
C. D.
?3. 下列四组线段中,不构成比例线段的一组是( )
A.?,?,?,? B.?,?,?,?
C.,,, D.?,?,?,?
?4. 已知点是线段的黄金分割点,且,则下列等式中成立的是( )
A. B.
C. D.
?5. 如图:是斜靠在墙上的楼梯,梯脚点距离墙,梯上点距墙,,则梯子长为( )
A. B. C. D.
?6. 如图,,,,,.若在边上有点,使与相似,则这样的点有( )
A.个 B.个 C.个 D.个
?7. 如图,是线段的黄金分割点,四边形、四边形都是正方形,且面积分别为、,四边形、四边形都是矩形,且面积分别为、,下列说法正确的是( )
A. B.
C. D.
?8. 若两个相似三角形的面积比为,那么这两个三角形的周长的比为( )
A. B.
C. D.
?9. 已知:如图,,则在下列比例中一定成立的是( )
A. B.
C. D.
?10. 如图,在钝角中,,,动点从点出发到点止.动点从点出发到点止.点运动的速度为,点运动的速度为.如果两点同时运动,那么当以点、、为顶点的三角形与相似时.运动的时间是( )
A.或 B.
C. D.或
二、 填空题 (本题共计 10 小题 ,每题 3 分 ,共计30分 , )
11. 在和中,,,分别是,的角平分线,且,与________(填“是”或“否”)相似.
?12. 如果两个相似三角形的相似比为,则这两个三角形的对应的高的比为________,对应角分线的比为________.
?13. 已知,和是它们的对应角平分线,且,,则与对应高的比为________.
?14. 有一棵松树在某一时刻的影子如图所示,同学小军站在处发现他的影子顶端恰好与树的影子顶端在处重合,此时小军测得自己影长,他与树底端距离,若小军身高,则树高约为________.
?15. 如图,已知与相交于点,且,,则________.
?16. 在平面直角坐标系中,已知点,,以原点为位似中心,相似比为,把缩小,则点对应点的坐标是________.
?17. 如图,直线,直线、与、、分别交于点、、、、、,若,,,则________.
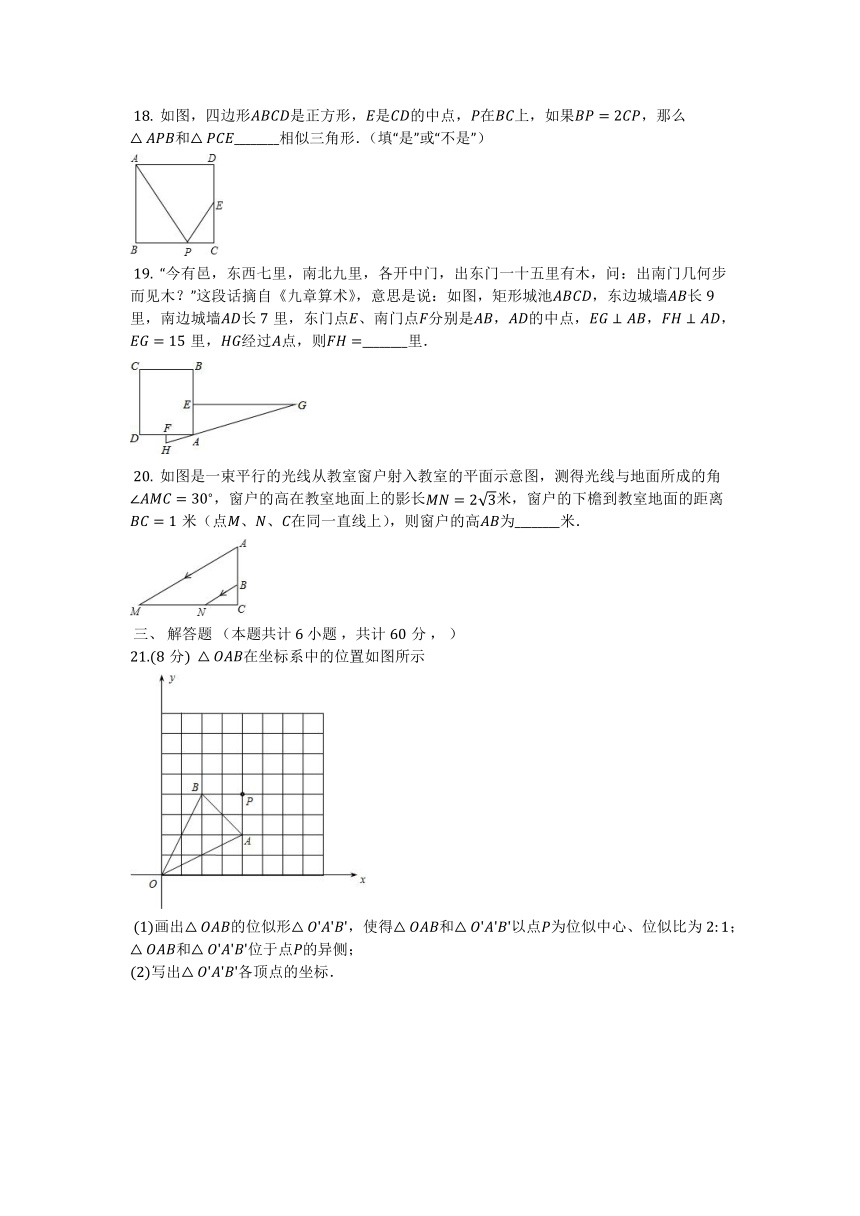
?18. 如图,四边形是正方形,是的中点,在上,如果,那么和________相似三角形.(填“是”或“不是”)
?19. “今有邑,东西七里,南北九里,各开中门,出东门一十五里有木,问:出南门几何步而见木?”这段话摘自《九章算术》,意思是说:如图,矩形城池,东边城墙长里,南边城墙长里,东门点、南门点分别是,的中点,,,里,经过点,则________里.
?20. 如图是一束平行的光线从教室窗户射入教室的平面示意图,测得光线与地面所成的角,窗户的高在教室地面上的影长米,窗户的下檐到教室地面的距离米(点、、在同一直线上),则窗户的高为________米.
三、 解答题 (本题共计 6 小题 ,共计60分 , )
21.(8分) 在坐标系中的位置如图所示
画出的位似形,使得和以点为位似中心、位似比为;和位于点的异侧;
写出各顶点的坐标.
?
22. (10分) 如图,在中,,,若,,求.
?
23. (10分) 如图,小明同学用自制的直角三角形纸板测量树的高度,他调整自己的位置,设法使斜边保持水平,并且边与点在同一直线上,已知纸板的两条直角边,,测得边离地面的高度,,求树高.
?
24.(10分) 如图,在矩形中,是边上任意一点(不与点,重合),作交的延长线于点.
求证:;
连接,为的中点,,,设,
①求点到的距离(用含的代数式表示);
②连接,设,求与之间的函数关系式,并直接写出的长度的最小值.
?
25.(10分) 已知:如图,在中,是边上的中点,且,,与相交于点,与相交于点.
求证:;
若的面积为,,求的长.
?
26.(12分) 如图,在中,,,,点从点出发沿方向向点运动,速度为,同时点从点出发沿方向向点运动,速度为,当一个运动点到达终点时,另一个运动
点也随之停止运动.
求、的长;
设点的运动时间为(秒),的面积为,当存在时,求与的函数关系式;
当点在上运动,使时,以点、、为顶点的三角形与是否相似,请说明理由.
答案
1. A
2. B
3. D
4. A
5. C
6. C
7. B
8. C
9. B
10. A
11. 否
12.
13.
14.
15.
16.
17.
18. 是
19.
20.
21. 解:画出如图所示的图形,
则为所求的三角形;
由图形可得:,,
.
22. 解:∵,,
∴,,
∴;
∴,
∵,,
∴,
∴,
即,
∴:,
即.
∵,
∴,
又∵,
∴,
∴,
∴,
∴.
23. 解:在和中,,
∴,
∴,
即,
解得,
∵,
∴,
即树高.
24. 证明:∵在矩形中,,
∴,
∵,
∴,
∵,
∴,
又∵,
∴;解:①如图,取的中点,连接,
∵为的中点,
∴,,
∵在矩形中,,
∴,即是点到的距离,
∵,,
∴,
∴,
即点到的距离为;
②∵,
∴,
∴,
∴,,,
∴,
∵,
∴在中,,
∴
∵,
当时,有最小值,
此时,的最小值是.
25. 证明:∵是边上的中点,
∴
∴.
∵,
∴.
∴.解:过作于.
∵,,
∴.
∵,
∴.
∴.
∴.
∵,
∴
∴.
∴.
26. 解:设,,在中,,
即:,
解得:,
∴,;
分两种情况:
①当点在边上运动时,过点作于.
∵,∴,,
∵,
∴,
∴,
,
②当点在边上运动时,过点作于,
∵,
∴,,
∵,
∴,
即:,
解得:,
∴
;当点在上运动,使时,以点、、为顶点的三角形与不相似.理由如下:
∵,
∴,
∵,
∴,
∴,
即:,
解得:,,
∴,
∴,
∴当点在上运动,使时,以点、、为顶点的三角形与不相似.
学校:__________ 班级:__________ 姓名:__________ 考号:__________
一、 选择题 (本题共计 10 小题 ,每题 3 分 ,共计30分 , )
1. 若,则的值为( )
A. B. C. D.
?2. 东海大桥全长千米,如果东海大桥在某张地图上的长为厘米,那么该地图上距离与实际距离的比为( )
A. B.
C. D.
?3. 下列四组线段中,不构成比例线段的一组是( )
A.?,?,?,? B.?,?,?,?
C.,,, D.?,?,?,?
?4. 已知点是线段的黄金分割点,且,则下列等式中成立的是( )
A. B.
C. D.
?5. 如图:是斜靠在墙上的楼梯,梯脚点距离墙,梯上点距墙,,则梯子长为( )
A. B. C. D.
?6. 如图,,,,,.若在边上有点,使与相似,则这样的点有( )
A.个 B.个 C.个 D.个
?7. 如图,是线段的黄金分割点,四边形、四边形都是正方形,且面积分别为、,四边形、四边形都是矩形,且面积分别为、,下列说法正确的是( )
A. B.
C. D.
?8. 若两个相似三角形的面积比为,那么这两个三角形的周长的比为( )
A. B.
C. D.
?9. 已知:如图,,则在下列比例中一定成立的是( )
A. B.
C. D.
?10. 如图,在钝角中,,,动点从点出发到点止.动点从点出发到点止.点运动的速度为,点运动的速度为.如果两点同时运动,那么当以点、、为顶点的三角形与相似时.运动的时间是( )
A.或 B.
C. D.或
二、 填空题 (本题共计 10 小题 ,每题 3 分 ,共计30分 , )
11. 在和中,,,分别是,的角平分线,且,与________(填“是”或“否”)相似.
?12. 如果两个相似三角形的相似比为,则这两个三角形的对应的高的比为________,对应角分线的比为________.
?13. 已知,和是它们的对应角平分线,且,,则与对应高的比为________.
?14. 有一棵松树在某一时刻的影子如图所示,同学小军站在处发现他的影子顶端恰好与树的影子顶端在处重合,此时小军测得自己影长,他与树底端距离,若小军身高,则树高约为________.
?15. 如图,已知与相交于点,且,,则________.
?16. 在平面直角坐标系中,已知点,,以原点为位似中心,相似比为,把缩小,则点对应点的坐标是________.
?17. 如图,直线,直线、与、、分别交于点、、、、、,若,,,则________.
?18. 如图,四边形是正方形,是的中点,在上,如果,那么和________相似三角形.(填“是”或“不是”)
?19. “今有邑,东西七里,南北九里,各开中门,出东门一十五里有木,问:出南门几何步而见木?”这段话摘自《九章算术》,意思是说:如图,矩形城池,东边城墙长里,南边城墙长里,东门点、南门点分别是,的中点,,,里,经过点,则________里.
?20. 如图是一束平行的光线从教室窗户射入教室的平面示意图,测得光线与地面所成的角,窗户的高在教室地面上的影长米,窗户的下檐到教室地面的距离米(点、、在同一直线上),则窗户的高为________米.
三、 解答题 (本题共计 6 小题 ,共计60分 , )
21.(8分) 在坐标系中的位置如图所示
画出的位似形,使得和以点为位似中心、位似比为;和位于点的异侧;
写出各顶点的坐标.
?
22. (10分) 如图,在中,,,若,,求.
?
23. (10分) 如图,小明同学用自制的直角三角形纸板测量树的高度,他调整自己的位置,设法使斜边保持水平,并且边与点在同一直线上,已知纸板的两条直角边,,测得边离地面的高度,,求树高.
?
24.(10分) 如图,在矩形中,是边上任意一点(不与点,重合),作交的延长线于点.
求证:;
连接,为的中点,,,设,
①求点到的距离(用含的代数式表示);
②连接,设,求与之间的函数关系式,并直接写出的长度的最小值.
?
25.(10分) 已知:如图,在中,是边上的中点,且,,与相交于点,与相交于点.
求证:;
若的面积为,,求的长.
?
26.(12分) 如图,在中,,,,点从点出发沿方向向点运动,速度为,同时点从点出发沿方向向点运动,速度为,当一个运动点到达终点时,另一个运动
点也随之停止运动.
求、的长;
设点的运动时间为(秒),的面积为,当存在时,求与的函数关系式;
当点在上运动,使时,以点、、为顶点的三角形与是否相似,请说明理由.
答案
1. A
2. B
3. D
4. A
5. C
6. C
7. B
8. C
9. B
10. A
11. 否
12.
13.
14.
15.
16.
17.
18. 是
19.
20.
21. 解:画出如图所示的图形,
则为所求的三角形;
由图形可得:,,
.
22. 解:∵,,
∴,,
∴;
∴,
∵,,
∴,
∴,
即,
∴:,
即.
∵,
∴,
又∵,
∴,
∴,
∴,
∴.
23. 解:在和中,,
∴,
∴,
即,
解得,
∵,
∴,
即树高.
24. 证明:∵在矩形中,,
∴,
∵,
∴,
∵,
∴,
又∵,
∴;解:①如图,取的中点,连接,
∵为的中点,
∴,,
∵在矩形中,,
∴,即是点到的距离,
∵,,
∴,
∴,
即点到的距离为;
②∵,
∴,
∴,
∴,,,
∴,
∵,
∴在中,,
∴
∵,
当时,有最小值,
此时,的最小值是.
25. 证明:∵是边上的中点,
∴
∴.
∵,
∴.
∴.解:过作于.
∵,,
∴.
∵,
∴.
∴.
∴.
∵,
∴
∴.
∴.
26. 解:设,,在中,,
即:,
解得:,
∴,;
分两种情况:
①当点在边上运动时,过点作于.
∵,∴,,
∵,
∴,
∴,
,
②当点在边上运动时,过点作于,
∵,
∴,,
∵,
∴,
即:,
解得:,
∴
;当点在上运动,使时,以点、、为顶点的三角形与不相似.理由如下:
∵,
∴,
∵,
∴,
∴,
即:,
解得:,,
∴,
∴,
∴当点在上运动,使时,以点、、为顶点的三角形与不相似.
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
