7.4长方体和正方体的体积课件(共17张PPT)
文档属性
| 名称 | 7.4长方体和正方体的体积课件(共17张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 565.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-01-22 17:54:02 | ||
图片预览



文档简介
课件17张PPT。
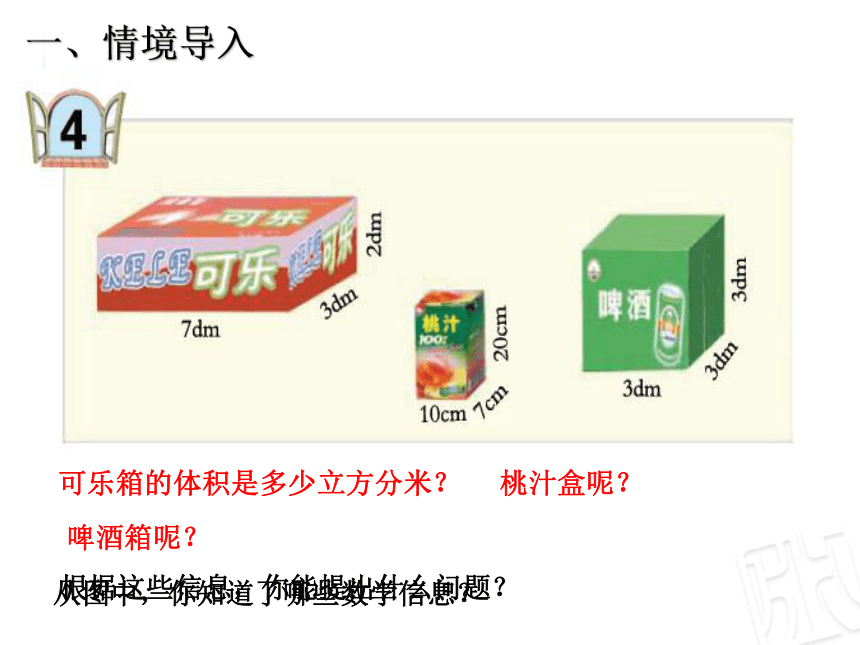
长方体和正方体的体积一、情境导入根据这些信息,你能提出什么问题?从图中,你知道了哪些数学信息?
可乐箱的体积是多少立方分米?
啤酒箱呢?
桃汁盒呢?二、合作探索
求可乐箱的体积,就是求长方体的体积。
怎样求长方体的体积呢?
我们知道:面积的大小等于含有“面积单位”数量的多少,那么体积的大小是不是也等于含有“体积单位”数量的多少呢?
二、合作探索 我们借助学具小组合作来研究求长方体体积的计算方法。合作要求:
1、发挥小组共同参与的精神,积极完成任 务。
2、小组长认真记录。
3、探究过程中认真思考交流:长方体的体积与小正方体的个数有什么关系?与长方体的长、宽、高有什么关系?
4、总结归纳长方体体积计算公式。
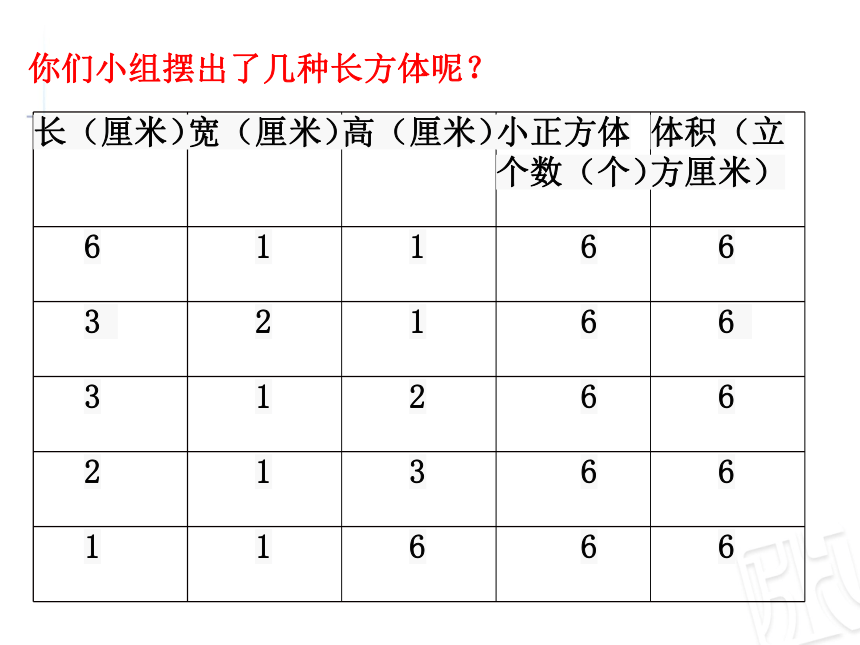
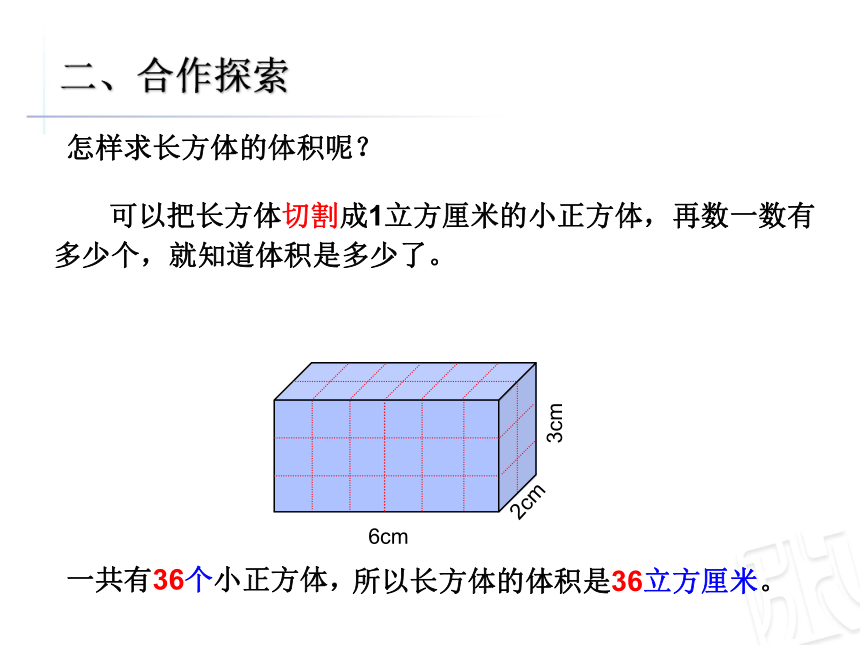
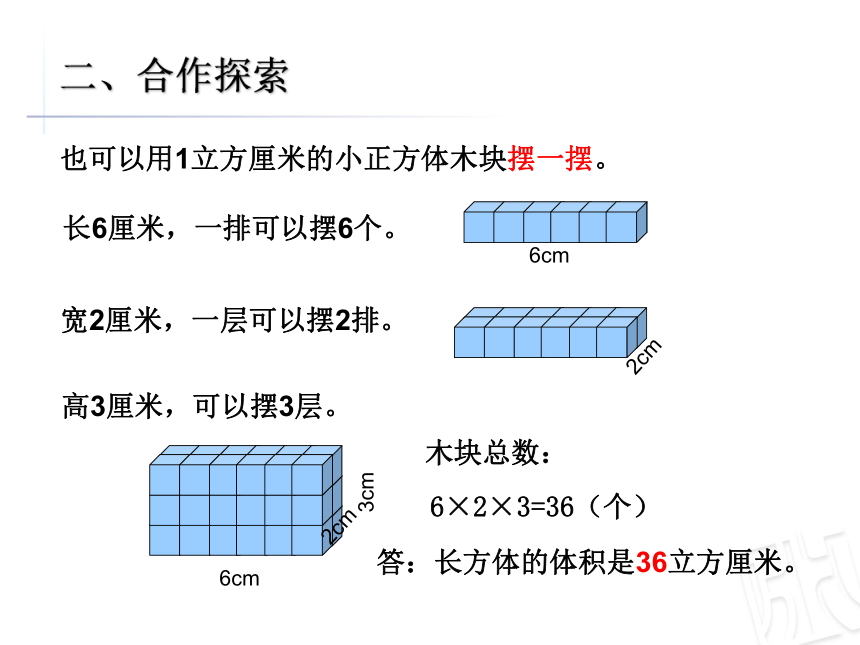
你们小组摆出了几种长方体呢? 二、合作探索一共有36个小正方体, 可以把长方体切割成1立方厘米的小正方体,再数一数有多少个,就知道体积是多少了。所以长方体的体积是36立方厘米。怎样求长方体的体积呢? 二、合作探索长6厘米,一排可以摆6个。宽2厘米,一层可以摆2排。高3厘米,可以摆3层。木块总数:6×2×3=36(个)答:长方体的体积是36立方厘米。2cm6cm3cm6cm2cm也可以用1立方厘米的小正方体木块摆一摆。二、合作探索4cm5cm2cm
木块总数:5×4×2=40(个)体积:5×4×2=40(立方厘米) 摆一个长5厘米,宽4厘米,高2厘米的长方体,并算出它的体积是多少立方厘米。答:长方体的体积是40立方厘米。二、合作探究回顾刚才的活动过程,想一想,物体的体积与它所含“体积单位”的数量有着怎样的关系?长方体所含“体积单位”的数量就是它们的体积。长方体所含“体积单位”的数量,等于长、宽、高的积。bɑh
长方体的体积 = 长×宽×高V = ɑbh 二、合作探索根据以上探索过程,如果v表示长方体的体积,ɑ表示长,b表示宽,h表示高,你能总结出长方体的体积计算公式吗?长宽高二、合作探索3cm3cm3cm
木块总数:3×3×3=27(个)体积:3×3×3=27(立方厘米) 摆一个棱长是3厘米的正方体,并算出它的体积是多少立方厘米。答:正方体的体积是27立方厘米。
正方体的体积=棱长×棱长×棱长V = ɑ·ɑ·ɑɑɑɑ二、合作探索
根据以上探索过程,如果v表示正方体的体积,a表示棱长,你能总结出正方体的体积计算公式吗?棱长棱长棱长ɑ﹒ɑ﹒ɑ也可以写作“ɑ3”,读作“ɑ的立方”,表示3个ɑ相乘。正方体的体积公式一般写成:V = ɑ3 你知道它们的体积各是多少吗?4227说一说计算下面图形的体积。自主练习 5×8×5=200(cm3)4×4×4=64(dm3)20×4×5=400(m3)练一练
公园南面要修一道长15米,宽24厘米,高3米的围墙。如果每立方米用砖525块,这道围墙一共用砖多少块?
长方体的体积 = 长×宽×高V = ɑbh 这节课你收获了什么?正方体的体积=棱长×棱长×棱长 V = ɑ·ɑ·ɑ V = ɑ3
bɑɑɑɑh课下探究长方体和正方体底面的面积叫作它们的底面积。你能用同一个公式来表示长方体和正方体体积的计算方法吗?长方体(或正方体)的体积 = 底面积×高
V = sh
长方体和正方体的体积一、情境导入根据这些信息,你能提出什么问题?从图中,你知道了哪些数学信息?
可乐箱的体积是多少立方分米?
啤酒箱呢?
桃汁盒呢?二、合作探索
求可乐箱的体积,就是求长方体的体积。
怎样求长方体的体积呢?
我们知道:面积的大小等于含有“面积单位”数量的多少,那么体积的大小是不是也等于含有“体积单位”数量的多少呢?
二、合作探索 我们借助学具小组合作来研究求长方体体积的计算方法。合作要求:
1、发挥小组共同参与的精神,积极完成任 务。
2、小组长认真记录。
3、探究过程中认真思考交流:长方体的体积与小正方体的个数有什么关系?与长方体的长、宽、高有什么关系?
4、总结归纳长方体体积计算公式。
你们小组摆出了几种长方体呢? 二、合作探索一共有36个小正方体, 可以把长方体切割成1立方厘米的小正方体,再数一数有多少个,就知道体积是多少了。所以长方体的体积是36立方厘米。怎样求长方体的体积呢? 二、合作探索长6厘米,一排可以摆6个。宽2厘米,一层可以摆2排。高3厘米,可以摆3层。木块总数:6×2×3=36(个)答:长方体的体积是36立方厘米。2cm6cm3cm6cm2cm也可以用1立方厘米的小正方体木块摆一摆。二、合作探索4cm5cm2cm
木块总数:5×4×2=40(个)体积:5×4×2=40(立方厘米) 摆一个长5厘米,宽4厘米,高2厘米的长方体,并算出它的体积是多少立方厘米。答:长方体的体积是40立方厘米。二、合作探究回顾刚才的活动过程,想一想,物体的体积与它所含“体积单位”的数量有着怎样的关系?长方体所含“体积单位”的数量就是它们的体积。长方体所含“体积单位”的数量,等于长、宽、高的积。bɑh
长方体的体积 = 长×宽×高V = ɑbh 二、合作探索根据以上探索过程,如果v表示长方体的体积,ɑ表示长,b表示宽,h表示高,你能总结出长方体的体积计算公式吗?长宽高二、合作探索3cm3cm3cm
木块总数:3×3×3=27(个)体积:3×3×3=27(立方厘米) 摆一个棱长是3厘米的正方体,并算出它的体积是多少立方厘米。答:正方体的体积是27立方厘米。
正方体的体积=棱长×棱长×棱长V = ɑ·ɑ·ɑɑɑɑ二、合作探索
根据以上探索过程,如果v表示正方体的体积,a表示棱长,你能总结出正方体的体积计算公式吗?棱长棱长棱长ɑ﹒ɑ﹒ɑ也可以写作“ɑ3”,读作“ɑ的立方”,表示3个ɑ相乘。正方体的体积公式一般写成:V = ɑ3 你知道它们的体积各是多少吗?4227说一说计算下面图形的体积。自主练习 5×8×5=200(cm3)4×4×4=64(dm3)20×4×5=400(m3)练一练
公园南面要修一道长15米,宽24厘米,高3米的围墙。如果每立方米用砖525块,这道围墙一共用砖多少块?
长方体的体积 = 长×宽×高V = ɑbh 这节课你收获了什么?正方体的体积=棱长×棱长×棱长 V = ɑ·ɑ·ɑ V = ɑ3
bɑɑɑɑh课下探究长方体和正方体底面的面积叫作它们的底面积。你能用同一个公式来表示长方体和正方体体积的计算方法吗?长方体(或正方体)的体积 = 底面积×高
V = sh
