高中数学第一章常用逻辑用语1.3.2命题的四种形式课件
文档属性
| 名称 | 高中数学第一章常用逻辑用语1.3.2命题的四种形式课件 |

|
|
| 格式 | zip | ||
| 文件大小 | 620.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-01-22 00:00:00 | ||
图片预览






文档简介
课件16张PPT。 1.3.2 命题的四种形式温故而知新命题的概念“若p,则q”型命题:其中p叫做命题的条件,
q叫做命题的结论. 观察下列四个命题的条件和结论
(1)若f(x)是正弦函数,则f(x)是周期函数;
(2)若f(x)是周期函数,则f(x)是正弦函数;
(3)若f(x)不是正弦函数,则f(x)不是周期函数;
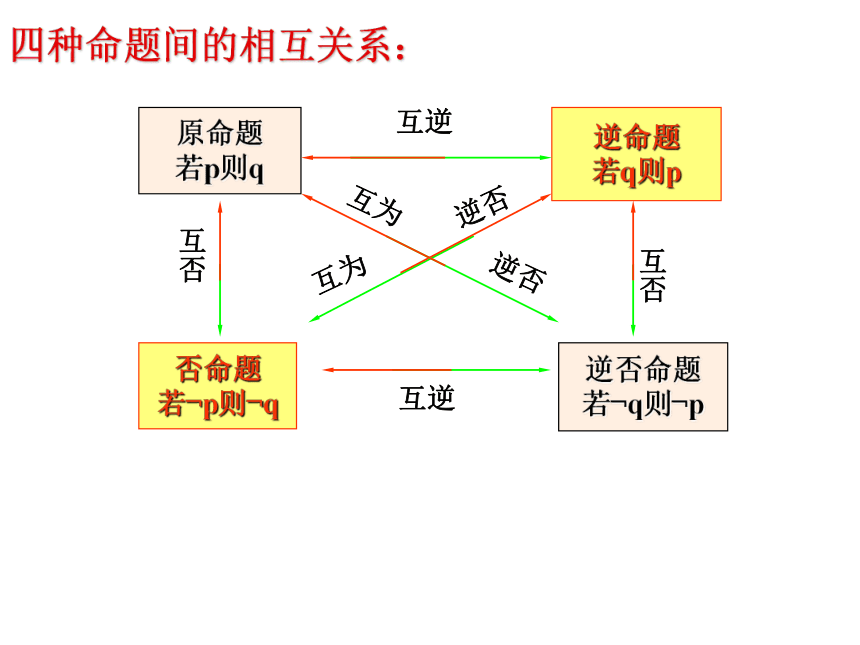
(4)若f(x)不是周期函数,则f(x)不是正弦函数;思考: 命题(1)与命题(2)(3)(4)的条件和结论之间分别有什么关系?原命题: 逆命题: 命题的四种形式:否命题: 逆否命题: 若p,则q.若q,则p.若?p,则?q.若?q,则?p. 换位换质换位换质四种命题间的相互关系:原命题
若p则q逆命题
若q则p否命题
若?p则?q逆否命题
若?q则?p互逆互逆互否互否互为 逆否互为 逆否例1 写出下列命题的逆命题、否命题与逆否命题,并判断它们的真假.逆命题: 若ab=0,则a=0.否命题:若a≠0,则ab≠0.逆否命题:若ab≠0,则a≠0. 真真假假(1)若a=0,则ab=0 (2) 若a2>b2,则a>b.逆命题: 若a>b,则a2>b2.否命题:若a2≤b2,则a≤b.逆否命题:若a≤b,则a2≤b2.假假假假(3) 当c>0时,若a>b,则ac>bc.逆命题:当c>0时,若ac>bc,则a>b.否命题:当c>0时,若a≤b,则ac≤bc.逆否命题:当c>0时,若ac≤bc,则a≤b.真真真真(4)四条边相等的四边形是正方形.改写:若一个四边形的四条边相等,则它是正方形.逆命题:若一个四边形是正方形,则它的四条边相等.否命题:若一个四边形的四条边不全相等,则它不是正方形.逆否命题:若一个四边形不是正方形,则它的四条边 不全相等.假真真假把以上四个小题中命题的真假性对比,你能发现什么规律吗?真真真真真假假假假假假假假真真真(1)互为逆否的两个命题等价(同真或同假)。
(2)互逆或互否两个命题不等价。练习:1、判断下列说法是否正确:
(1)一个命题的逆命题为真,它的逆否命题不一定为真。
(2)一个命题的否命题为真,它的逆命题一定为真。
2、如果一个命题的逆命题为假命题,则它的否命题为( )
A. 一定是假命题 B. 不一定是假命题
C. 一定是真命题 D. 有可能是真命题练习3、写出下列命题的否命题。
练习:正难则反深入探究命题的否定(“非”命题)与命题的否命题是一回事儿吗???例:写出下面命题的否命题和命题的否定,并判断真假?:
????????面积相等的三角形是全等三角形。真否命题:命题的否定:面积相等的三角形不是全等三角形。面积不相等的三角形不是全等三角形。真假结论:命题的否定只否定命题的结论,
而否命题对条件和结论同时否定。课堂小结:原命题: 逆命题: 否命题: 逆否命题: 若p则q.若q则p.若?p则?q.若?q则?p. 1、四种命题形式:2、四种命题间的相互关系及其真假性的关系:学到了什么?(1)互为逆否的两个命题等价(同真或同假) 。
(2)互逆或互否两个命题不等价。作业:
教材23页 练习 A、练习B 观察下面四个命题:
(1)若f(x)是正弦函数,则f(x)是周期函数;
(2)若f(x)是周期函数,则f(x)是正弦函数;
(3)若f(x)不是正弦函数,则f(x)不是周期函数;
(4)若f(x)不是周期函数,则f(x)不是正弦函数;说出其中任意两个命题之间的相互关系,
并判断真假。
谢谢欣赏
q叫做命题的结论. 观察下列四个命题的条件和结论
(1)若f(x)是正弦函数,则f(x)是周期函数;
(2)若f(x)是周期函数,则f(x)是正弦函数;
(3)若f(x)不是正弦函数,则f(x)不是周期函数;
(4)若f(x)不是周期函数,则f(x)不是正弦函数;思考: 命题(1)与命题(2)(3)(4)的条件和结论之间分别有什么关系?原命题: 逆命题: 命题的四种形式:否命题: 逆否命题: 若p,则q.若q,则p.若?p,则?q.若?q,则?p. 换位换质换位换质四种命题间的相互关系:原命题
若p则q逆命题
若q则p否命题
若?p则?q逆否命题
若?q则?p互逆互逆互否互否互为 逆否互为 逆否例1 写出下列命题的逆命题、否命题与逆否命题,并判断它们的真假.逆命题: 若ab=0,则a=0.否命题:若a≠0,则ab≠0.逆否命题:若ab≠0,则a≠0. 真真假假(1)若a=0,则ab=0 (2) 若a2>b2,则a>b.逆命题: 若a>b,则a2>b2.否命题:若a2≤b2,则a≤b.逆否命题:若a≤b,则a2≤b2.假假假假(3) 当c>0时,若a>b,则ac>bc.逆命题:当c>0时,若ac>bc,则a>b.否命题:当c>0时,若a≤b,则ac≤bc.逆否命题:当c>0时,若ac≤bc,则a≤b.真真真真(4)四条边相等的四边形是正方形.改写:若一个四边形的四条边相等,则它是正方形.逆命题:若一个四边形是正方形,则它的四条边相等.否命题:若一个四边形的四条边不全相等,则它不是正方形.逆否命题:若一个四边形不是正方形,则它的四条边 不全相等.假真真假把以上四个小题中命题的真假性对比,你能发现什么规律吗?真真真真真假假假假假假假假真真真(1)互为逆否的两个命题等价(同真或同假)。
(2)互逆或互否两个命题不等价。练习:1、判断下列说法是否正确:
(1)一个命题的逆命题为真,它的逆否命题不一定为真。
(2)一个命题的否命题为真,它的逆命题一定为真。
2、如果一个命题的逆命题为假命题,则它的否命题为( )
A. 一定是假命题 B. 不一定是假命题
C. 一定是真命题 D. 有可能是真命题练习3、写出下列命题的否命题。
练习:正难则反深入探究命题的否定(“非”命题)与命题的否命题是一回事儿吗???例:写出下面命题的否命题和命题的否定,并判断真假?:
????????面积相等的三角形是全等三角形。真否命题:命题的否定:面积相等的三角形不是全等三角形。面积不相等的三角形不是全等三角形。真假结论:命题的否定只否定命题的结论,
而否命题对条件和结论同时否定。课堂小结:原命题: 逆命题: 否命题: 逆否命题: 若p则q.若q则p.若?p则?q.若?q则?p. 1、四种命题形式:2、四种命题间的相互关系及其真假性的关系:学到了什么?(1)互为逆否的两个命题等价(同真或同假) 。
(2)互逆或互否两个命题不等价。作业:
教材23页 练习 A、练习B 观察下面四个命题:
(1)若f(x)是正弦函数,则f(x)是周期函数;
(2)若f(x)是周期函数,则f(x)是正弦函数;
(3)若f(x)不是正弦函数,则f(x)不是周期函数;
(4)若f(x)不是周期函数,则f(x)不是正弦函数;说出其中任意两个命题之间的相互关系,
并判断真假。
谢谢欣赏
