第三章 圆 最新测试卷(内含详细答案)
文档属性
| 名称 | 第三章 圆 最新测试卷(内含详细答案) |  | |
| 格式 | zip | ||
| 文件大小 | 289.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-01-23 09:49:24 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
北师大版九年级数学下册第三章〖圆〗最新测试卷
(总分:100分,用时:45分钟)
学校:___________姓名:___________班级:___________得分:___________
一、单选题:(共10题,30分)
1.如右图,已知A,B,C,D是圆上的点,弧AD=弧BC,AC,BD交于点E,则下列结论正确的是( )
AB=AD B .BE=CD C. AC=BD D. BE=AD
如右图,在⊙O中, = ,∠AOB=40°,则∠ADC的度数是( )
A、40° B、30° C、20° D、15°
3.如右图,在⊙O中,若点C是的中点,∠A=50°,则∠BOC=( )
A.40° B.45° C.50° D.60°
4.半径为3的圆中,一条弦长为4,则圆心到这条弦的距离是( )
A.3 B.4 C. D.
5.如图,A,B,C,D四点在⊙O上,四边形ABCD的一条外角∠DCE=70°,则∠BOD等于( )
A.35° B.70° C.110° D.140°
6.如图,四边形ABCD为⊙O的内接四边形,若∠BCD=110°,则∠BAD为( )
A.140° B.110° C.90° D.70°
7.如图,⊙O的半径为2,点A的坐标为(2,2),直线AB为⊙O的切线,B为切点.则B点的坐标为( )
A.(﹣ , ) B.(﹣,1) C.(﹣ , ) D.(﹣1,)
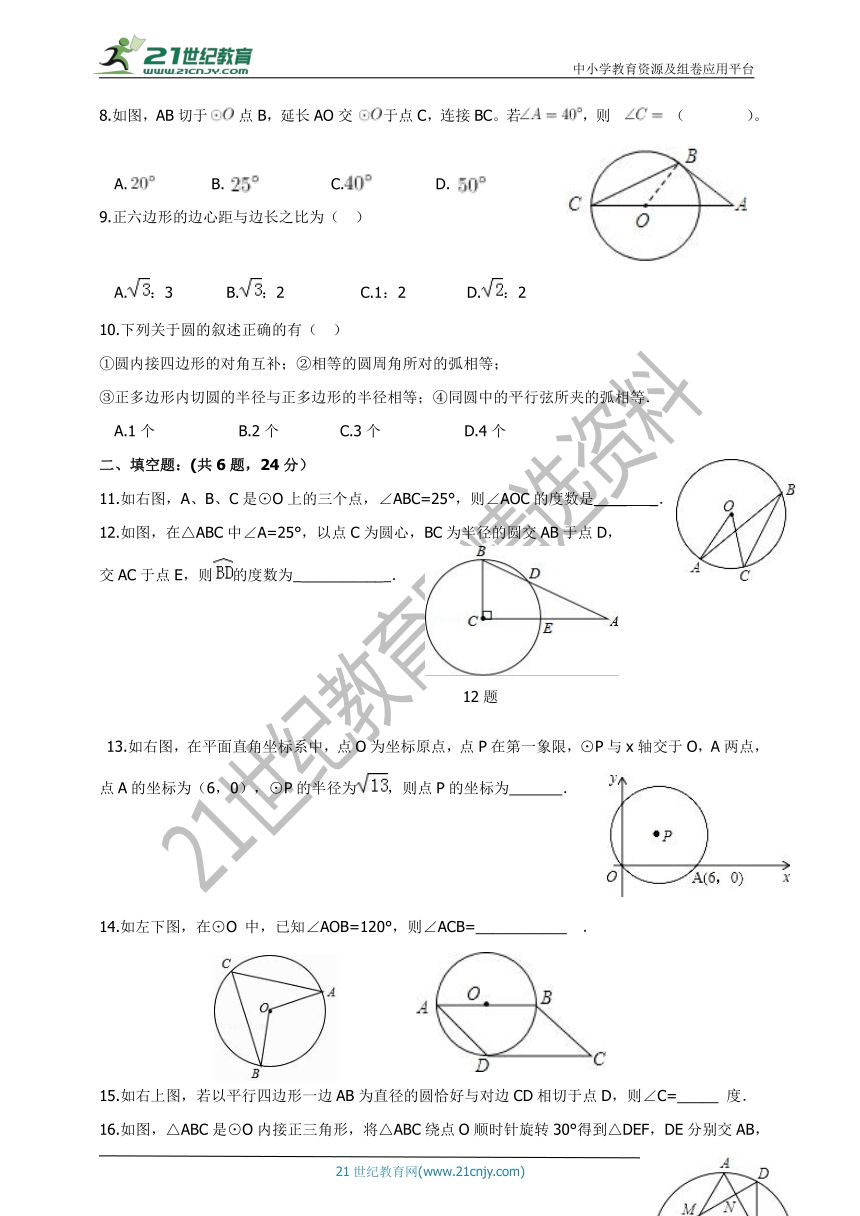
8.如图,AB切于 点B,延长AO交 于点C,连接BC。若 ,则 ( )。
A. B. C. D.
9.正六边形的边心距与边长之比为( )
A.:3 B.:2 C.1:2 D.:2
10.下列关于圆的叙述正确的有( )
①圆内接四边形的对角互补;②相等的圆周角所对的弧相等;
③正多边形内切圆的半径与正多边形的半径相等;④同圆中的平行弦所夹的弧相等.
A.1个 B.2个 C.3个 D.4个
二、填空题:(共6题,24分)
11.如右图,A、B、C是⊙O上的三个点,∠ABC=25°,则∠AOC的度数是____ _
.
12.如图,在△ABC中∠A=25°,以点C为圆心,BC为半径的圆交AB于点D,
交AC于点E,则的度数为 __________ .
13.如右图,在平面直角坐标系中,点O为坐标原点,点P在第一象限,⊙P与x轴交于O,A两点,点A的坐标为(6,0),⊙P的半径为,则点P的坐标为 .
14.如左下图,在⊙O 中,已知∠AOB=120°,则∠ACB=___________ .
15.如右上图,若以平行四边形一边AB为直径的圆恰好与对边CD相切于点D,则∠C=_____ 度.
16.如图,△ABC是⊙O内接正三角形,将△ABC绕点O顺时针旋转30°得到△DEF,DE分别交AB,AC于点M,N,DF交AC于点Q,则有以下结论:
①∠DQN=30°;②△DNQ≌△ANM;③△DNQ的周长等于AC的长;④NQ=QC.
其中正确的结论是 __________ .(把所有正确的结论的序号都填上)
三、问答题:(共2题,16分)
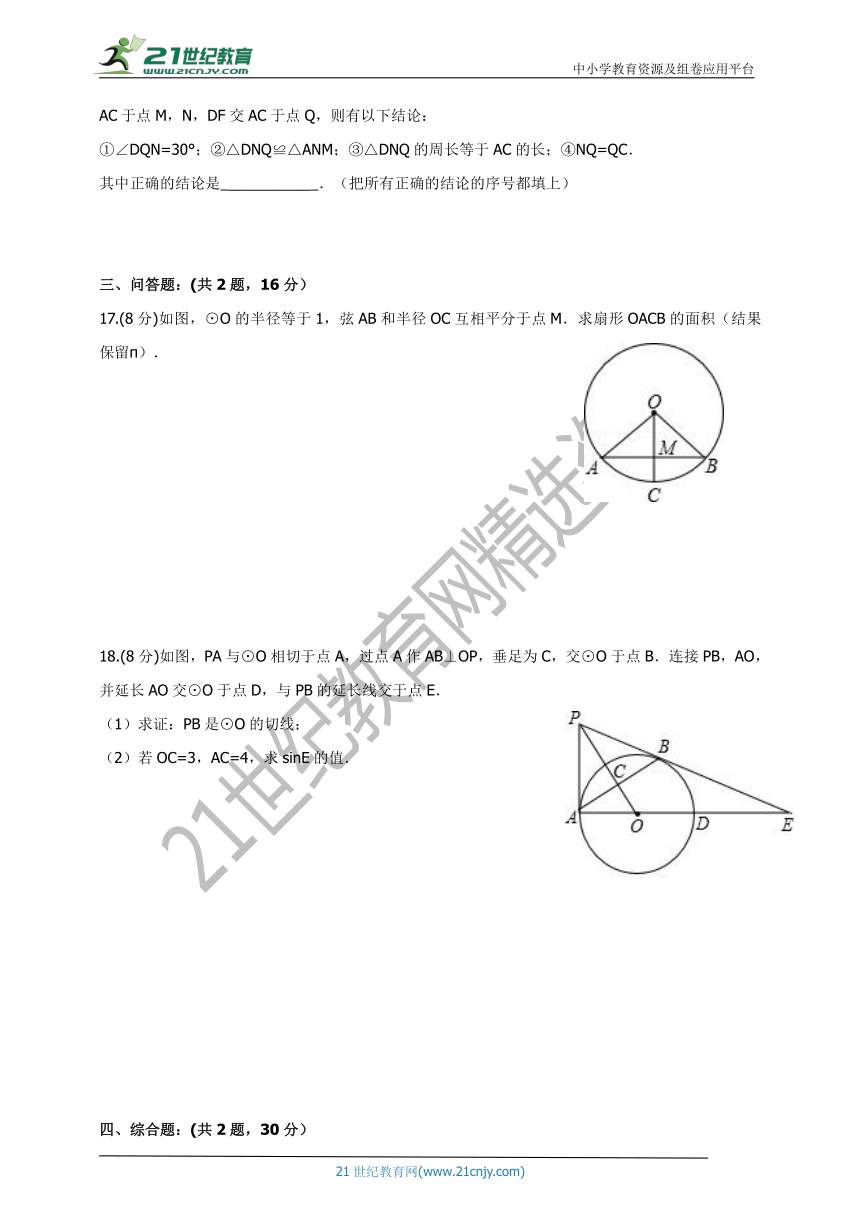
17.(8分)如图,⊙O的半径等于1,弦AB和半径OC互相平分于点M.求扇形OACB的面积(结果保留π).
18.(8分)如图,PA与⊙O相切于点A,过点A作AB⊥OP,垂足为C,交⊙O于点B.连接PB,AO,并延长AO交⊙O于点D,与PB的延长线交于点E.
(1)求证:PB是⊙O的切线;
(2)若OC=3,AC=4,求sinE的值.
四、综合题:(共2题,30分)
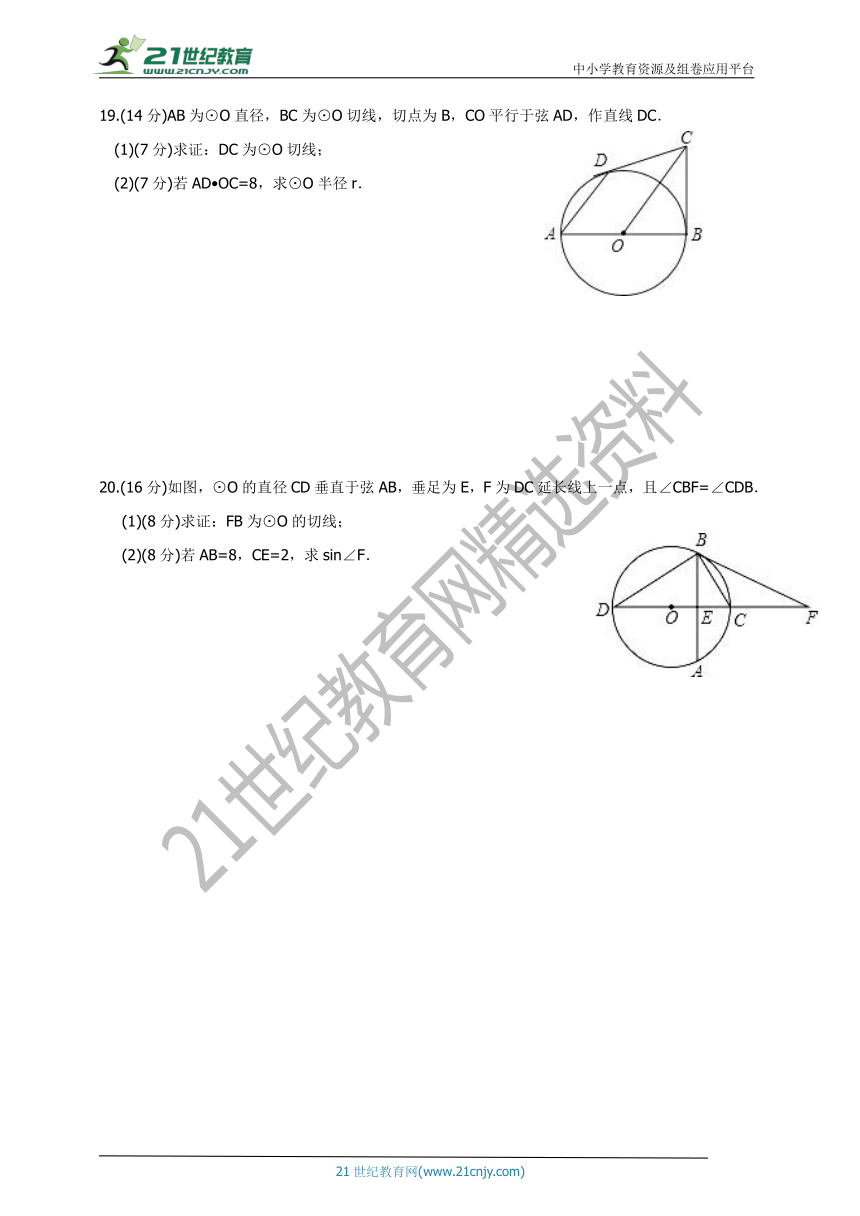
19.(14分)AB为⊙O直径,BC为⊙O切线,切点为B,CO平行于弦AD,作直线DC.
(1)(7分)求证:DC为⊙O切线;
(2)(7分)若AD?OC=8,求⊙O半径r.
20.(16分)如图,⊙O的直径CD垂直于弦AB,垂足为E,F为DC延长线上一点,且∠CBF=∠CDB.
(1)(8分)求证:FB为⊙O的切线;
(2)(8分)若AB=8,CE=2,求sin∠F.
参考答案与试题解析
一、选择题
1-5、CCACD 6-10、DDBBB
11:50° 12:50° 13:(3,2) 14:60° 15:45 16:①②③
16、题目解析:解:连结OA、OD、OF、OC、DC、AD、CF,如图,
∵△ABC绕点O顺时针旋转30°得到△DEF,
∴∠AOD=∠COF=30°,
∴∠ACD=∠AOD=15°,∠FDC=∠COF=15°,
∴∠DQN=∠QCD+∠QDC=15°+15°=30°,所以①正确;
同理可得∠AMN=30°,
∵△DEF为等边三角形,
∴DE=DF,
∴弧DE=弧DF,
∴弧AE+弧AD=弧DC+弧CF,
而弧AD=弧CF,
∴弧AE=弧DC,
∴∠ADE=∠DAC,
∴ND=NA,
在△DNQ和△ANM中,,
∴△DNQ≌△ANM(AAS),所以②正确;
∵∠ACD=15°,∠FDC=15°,
∴QD=QC,
而ND=NA,
∴ND+QD+NQ=NA+QC+NQ=AC,
即△DNQ的周长等于AC的长,所以③正确;
∵△DEF为等边三角形,
∴∠NDQ=60°,
而∠DQN=30°,
∴∠DNQ=90°,
∴QD>NQ,
∵QD=QC,
∴QC>NQ,所以④错误.
17.正确答案:解:∵弦AB和半径OC互相平分
∴OC⊥AB,OM=MC= OC= OA
在Rt△OAM中,sinA= ,
∴∠A=30°又∵OA=OB,∴∠B=∠A=30°∴∠AOB=120°∴S扇形=
18.正确答案:(1)证明:连接OB∵PO⊥AB,
∴AC=BC,
∴PA=PB
在△PAO和△PBO中
∴△PAO和≌△PBO
∴∠OBP=∠OAP=90°
∴PB是⊙O的切线.
(2)连接BD,则BD∥PO,且BD=2OC=6
在Rt△ACO中,OC=3,AC=4
∴AO=5
在Rt△ACO与Rt△PAO中,
∠APO=∠APO,
∠PAO=∠ACO=90°
∴△ACO?△PAO
=
∴PO= , PA=
∴PB=PA=
在△EPO与△EBD中,
BD∥PO
∴△EPO∽△EBD
∴=,
解得EB=,
PE=,
∴sinE= =
19.
(1).正确答案:证明:连接OD. ∵OA=OD,
∴∠A=∠ADO.
∵AD∥OC,
∴∠A=∠BOC,∠ADO=∠COD,
∴∠BOC=∠COD.
∵在△OBC与△ODC中,
,
∴△OBC≌△ODC(SAS),
∴∠OBC=∠ODC,
又∵BC是⊙O的切线,
∴∠OBC=90°,
∴∠ODC=90°,
∴DC是⊙O的切线;
(2).正确答案:解:连接BD.
∵在△ADB与△ODC中, ,
∴△ADB∽△ODC,∴AD:OD=AB:OC,
∴AD?OC=OD?AB=r?2r=2r2 ,
即2r2=8,故r=2.
20.(1).正确答案:证明:连接OB.
∵CD是直径,∴∠CBD=90°,
又∵OB=OD,∴∠OBD=∠D,
又∠CBF=∠D,∴∠CBF=∠OBD,
∴∠OBF=90°,即OB⊥BF,
∴FB是圆的切线
.正确答案:解:∵CD是圆的直径,CD⊥AB,
∴BE=AB=4,设圆的半径是R,在直角△OEB中,根据勾股定理得:R2=(R﹣2)2+42,
解得:R=5,
∵∠BOE=∠FOB,∠BEO=∠OBF,
∴△OBE∽△OBF,
∴OB2=OE?OF,
∴OF= = ,
则在直角△OBF中,sinF= = = .
12题
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
