1.1 等腰三角形（1）-试卷

1.1 等腰三角形（1）
班级：___________姓名：___________得分：__________
（满分：100分，考试时间：40分钟）
一．选择题（共5小题，每题8分）
1．如图，在△ABC 中，AB＝AC，D 是 BC 的中点，∠B＝40°，则∠BAD＝（ ）
/
A．100° B．80° C．50° D．40°
2．△ABC中，AB=AC，D是BC中点，下列结论中不一定正确的是（ ）
A．∠B=∠C B．AD⊥BC C．AD平分∠BAC D．AB=2BD
3．已知等腰三角形的一个外角等于100°，则它的顶角是（ ）
A．80° B．20° C．80°或20° D．不能确定
4．等腰三角形ABC中，AB=AC，AD是角平分线，则“①AD⊥BC，②BD=DC，③∠B=∠C，④∠BAD=∠CAD”中，结论正确的个数是（ ）
A．4 B．3 C．2 D．1
5．等腰三角形的顶角是n°，那么它的一腰上的高与底边的夹角等于（ ）
A． B． C． D．
二．填空题（共4小题，每题5分）
6．周长为16的等腰三角形，其一边长为6，则另两边长为___________________．
7．若等腰三角形中有一个角等于40°，则这个等腰三角形的顶角的度数为___ _____．
8．若等腰三角形的一个外角为50°，则它的底角为_________度．
9．如图，△ABC的周长为16，且AB=AC，AD⊥BC于D，△ACD的周长为12，那么AD的为 ．
/
三．解答题（共3小题，第10题10分，第11、12题各15分）
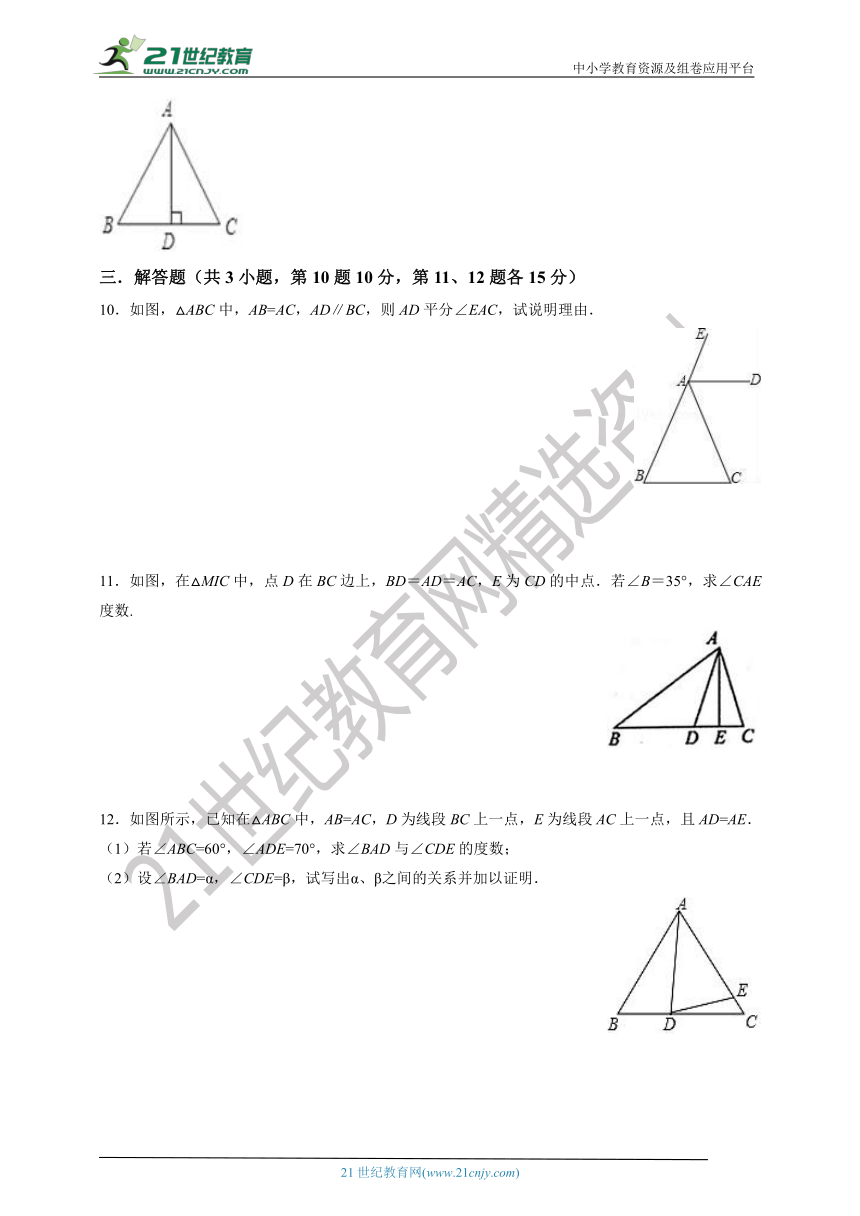
10．如图，△ABC中，AB=AC，AD∥BC，则AD平分∠EAC，试说明理由．
/
11．如图，在△MIC中，点D在BC边上，BD＝AD＝AC，E为CD的中点．若∠B＝35°，求∠CAE度数.
/
12．如图所示，已知在△ABC中，AB=AC，D为线段BC上一点，E为线段AC上一点，且AD=AE．
（1）若∠ABC=60°，∠ADE=70°，求∠BAD与∠CDE的度数；
（2）设∠BAD=α，∠CDE=β，试写出α、β之间的关系并加以证明．
/
试题解析
/
2．D
【解析】根据等腰三角形的性质逐项分析即可.
解：A.等腰三角形的两个底角相等，所以∠B=∠C，故A项结论正确；
B、C项，等腰三角形顶角的平分线，底边上的中线以及底边上的高的重合，因为D是BC中点，，所以AD⊥BC，AD平分∠BAC，故B、C项结论正确；
D.由于三角形角度不确定，故无法得到AB和BD的关系，故D项结论错误.
故选D.
3．C
【解析】解：①若100°是顶角的外角，则顶角=180°-100°=80°；
②若100°是底角的外角，则底角=180°-100°=80°，那么顶角=180°-2×80°=20°．
故选C．
4．A
【解析】根据等边对等角，“三线合一”：等腰三角形的顶角平分线、底边上的高和底边上的中线重合，依次分析各小题即可。
解：∵AB=AC，AD是角平分线，
根据“三线合一”可得AD⊥BC，BD=DC，
∵AB=AC，
∴∠B=∠C，
∵AD是角平分线，
∴∠BAD=∠CAD
结论正确是①②③④共4个，故选A.
5．C
【解析】如图，
/
当△ABC为锐角三角形时，已知∠A= n°，则∠C=/.
所以∠DBC=/.当△ABC为钝角三角形时，同理可得.
6．5，5或 4，6．
【解析】当腰为6时，则另两边长为6、4，此时三边满足三角形三边关系；
当底边为6时，则另两边长为5、5，此时三边满足三角形三边关系；
故答案为：6，4或5，5．
7．40°或100°．
【解析】∵等腰三角形中有一个角等于40°，
∴①若40°为顶角，则这个等腰三角形的顶角的度数为40°；
②若40°为底角，则这个等腰三角形的顶角的度数为：180°-40°×2=100°．
∴这个等腰三角形的顶角的度数为：40°或100°．
8．25
【解析】根据题意分情况讨论，一种情况是当底角的外角为50°时，不含题意舍去；另一种情况顶角的外角为50°时利用邻补角的关系求出顶角，继而利用三角形内角和以及等腰三角形的两个底角相等的性质计算即可．
9．4
【解析】∵AB=AC，AD⊥BC，
∴BD=CD，
又∵△ABC的周长=AB+AC+BC=2（AC+CD）=16，
∴AC+CD=8，
又△ACD的周长=AC+AD+CD=12，
∴AD=4.
10．证明见解析
【解析】由等边对等角可得到∠B=∠C，再根据平行线的性质可得到∠EAD=∠B=∠C=∠DAC，即AD平分∠EAC．
解：∵AB=AC
∴∠B=∠C
∵AD∥BC
∴∠EAD=∠B=∠C=∠DAC
∴AD平分∠EAC．
11．∠CAE＝20°.
【解析】根据等边对等角求出∠BAD，从而求出∠ADC，在等腰三角形ADC中，由三线合一求出∠CAE.
解：∵BD＝AD，
∴∠BAD=∠B=35°，
∴∠ADE=∠BAD＋∠B=70°，
∵AD=AC，
∴∠C=∠ADE=70°，
∵AD=AC，AE平分DC，
∴AE⊥EC，（三线合一）.
∴∠EAC=90°－∠C=20°.
12．（1）20°，10°；（2）结论：α=2β，理由见解析.
【解析】（1）根据∠BAD=∠BAC-∠DAE，∠AED=∠CDE+∠C，进行计算即可解决问题；
（2）α=2β，理由是：设∠BAC=x°，∠DAE=y°，则α=x°-y°，同理求出∠ACB=
180°???°
2
和∠AED=
180°???°
2
，利用外角定理得：β=∠AED-∠ACB，代入可得结论．
解：（1）∵AB=AC，
∴∠B=∠C=60°，
∴∠BAC=60°，
∵AD=AE，
∴∠ADE=∠AED=70°，
∴∠DAE=40°，
∴∠BAD=∠BAC-∠DAE=20°，
∵∠AED=∠CDE+∠C，
∴∠CDE=70°-60°=10°．
（2）结论：α=2β，理由是：
设∠BAC=x°，∠DAE=y°，则α=x°-y°，
∵∠ACB=∠ABC，
∴∠ACB=
180°???°
2
，
∵∠ADE=∠AED，
∴∠AED=
180°???°
2
，
∴β=∠AED-∠ACB=
180°???°
2
-
180°???°
2
=
??°???°
2
=
α
2
，
∴α=2β；
/