北师大版数学七年级下册第四章同步课时精炼【4.3(3课时)】
文档属性
| 名称 | 北师大版数学七年级下册第四章同步课时精炼【4.3(3课时)】 |  | |
| 格式 | zip | ||
| 文件大小 | 375.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-01-23 16:29:01 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
4.3 探索三角形全等的条件(1)
一、填空题
1.下列三角形全等的是
2.三边对应相等的两个三角形全等,简写为 或
3.三角形三边的长度确定了,它的形状和大小就完全确定了。三角形的这个性质叫做三角形的
二、解答题
4.已知:如图1,AB=AC,BD=DC,求证:△ABD≌△ACD
证明:在△ABD和△ACD中
∴ △ABD △ACD( )
5.已知:如图2,AM=AN,BM=BN,求证:△AMB≌△ANB
证明:在△AMB和△ANB中
∴ ≌ ( )
6.已知:如图3,AD=CB,AB=CD 求证:∠B=∠D
证明:在 中
∴ △ ≌△ ( )
∴∠B=∠D(全等三角形对应角相等)
4.3探索三角形全等的条件(2)
一、填空题
1.两角和它们的夹边对应相等的两个三角形全等,简写成 或
2.两角和其中一角的对边对应相等的两个三角形全等,简写成 或
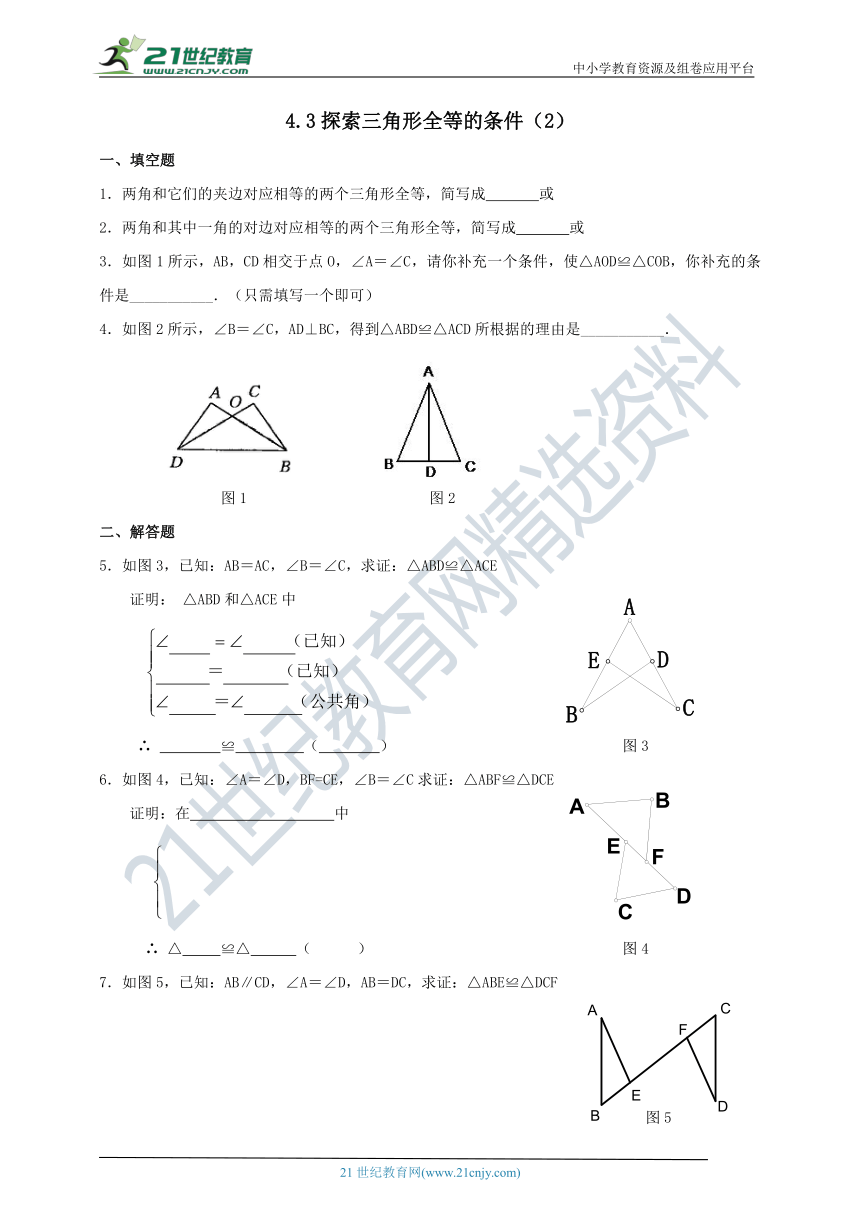
3.如图1所示,AB,CD相交于点O,∠A=∠C,请你补充一个条件,使△AOD≌△COB,你补充的条件是___________.(只需填写一个即可)
4.如图2所示,∠B=∠C,AD⊥BC,得到△ABD≌△ACD所根据的理由是___________.
图1 图2
二、解答题
5.如图3,已知:AB=AC,∠B=∠C,求证:△ABD≌△ACE
证明: △ABD和△ACE中
∴ ≌ ( ) 图3
6.如图4,已知:∠A=∠D,BF=CE,∠B=∠C求证:△ABF≌△DCE
证明:在 中
∴ △ ≌△ ( ) 图4
7.如图5,已知:AB∥CD,∠A=∠D,AB=DC,求证:△ABE≌△DCF
图5
4.3探索三角形全等的条件(3)
一、选择题
1.如图1所示,∠CAB=∠DBA,AC=BD,得到△CAB≌△DBA所根据的理由是( )
A.SAS B.SSS C.AAS D.ASA
2.下列条件中,不能判定两个三角形全等的条件是( )
A.两边一角对应相等 B.两角一边对应相等
C.三边对应相等 D.两边和它们的夹角对应相等 图1
二、填空题
3.两边和它们的夹角对应相等的两个三角形全等,简写成 或
4.如图2所示,在△ABC和△DEF中,AB=DE,∠B=∠E,要使△ABC≌△DEF,需要补充的一个条件是_______(只需填写一个即可).
图2
三、解答题
5.如图3,已知AO=BO,CO=DO,求证:△AOC≌△BOD
证明:在 中
∴ △ ≌△ ( ) 图3
6.如图4,已知:BD=CD,AD⊥BC,求证:△ABD≌△ACD
7.如图5,已知:AB=AC,E、D分别是AB、AC的中点, 图4
求证:△ABD≌△ACD
4.3 探索三角形全等的条件(1)
1.(1)和(3)、(2)和(4) 2.边边边,SSS 3.稳定性
4.BD,BD,≌,SSS 5.AN,已知,BM,AB,AB,△AMB,△ANB,SSS
6.证明:在△ABC和△CDA中
∵
∴△ABC≌△CDA(SSS)
∴∠B=∠D(全等三角形对应角相等)
4.3探索三角形全等的条件(2)
1.角边角,ASA 2.角角边,AAS 3.AO=CO(或DO=BO或AD=BC) 4.AAS
5.B,C,AB,AC,A,A,△ABD,△ACE,ASA
6.证明:在△ABF和△DCE中
∵
∴△ABF≌△DCE(AAS)
7.证明:∵AB∥CD
∴∠B=∠C
在△ABE和△DCF中
∵
∴△ABE≌△DCF(ASA)
4.3探索三角形全等的条件(3)
1.A 2.A
3.边角边,SAS 4.∠A=∠D(或∠C=∠F或BC=EF)
5.证明:在△AOC和△BOD中
∵
∴△AOC≌△BOD(SAS)
6.证明:∵AB⊥CD
∴∠ADB=∠ADC=90°
在△ABD和△ACD中
∵
∴△ABD≌△ACD(SAS)
7. 证明略
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
