江苏省扬州市2019届高三上学期期末检测数学试题(解析版)
文档属性
| 名称 | 江苏省扬州市2019届高三上学期期末检测数学试题(解析版) |  | |
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-01-27 16:20:39 | ||
图片预览




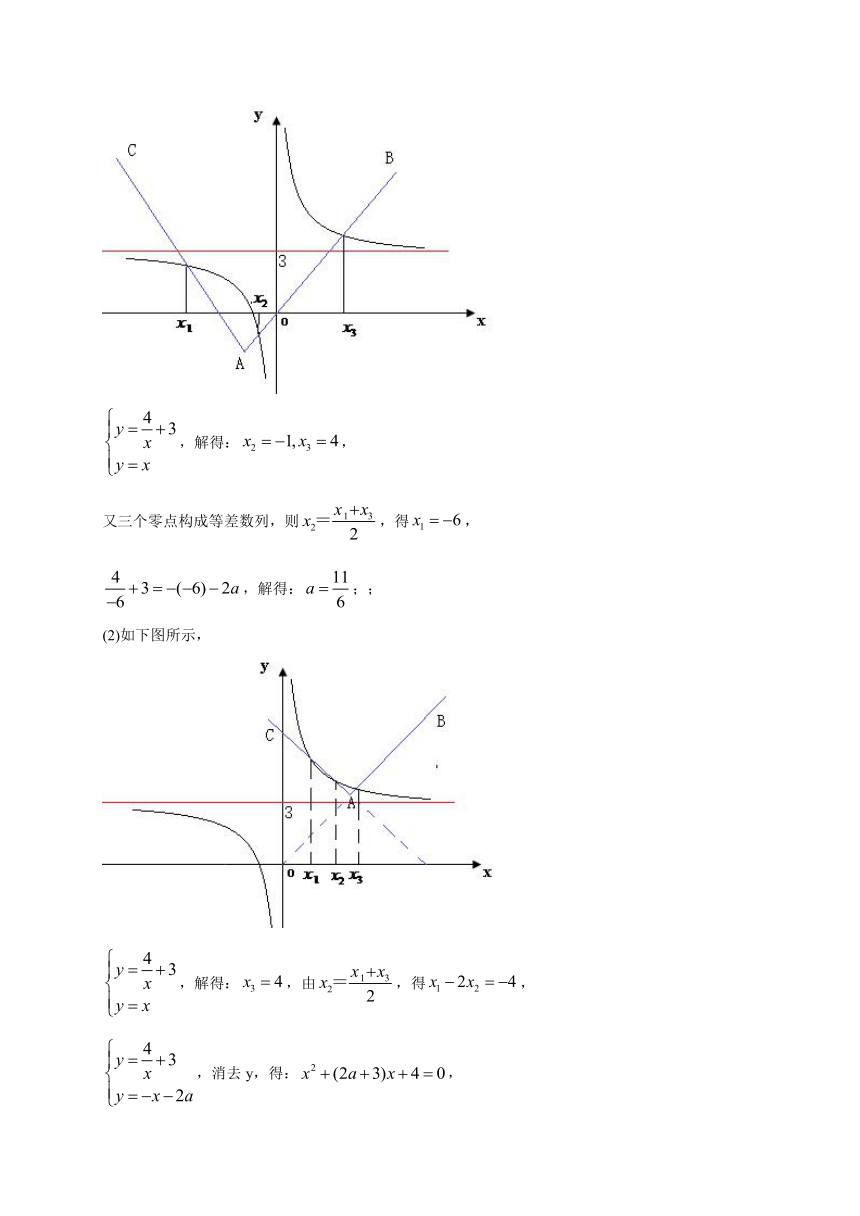
文档简介
扬州市2019届高三上学期期末检测试题
数 学2019.01
第一部分
一、填空题(本大题共14小题,每小题5分,共计70分.不需要写出解答过程,请将答案填写在答题卡相应的位置上.)
1.已知集合M={﹣2,﹣1,0},N=,则MN= .
答案:
考点:集合的运算,指数运算。
解析:N==,所以,MN=
2.若i是虚数单位,且复数z满足,则= .
答案:
考点:复数的运算,复数的模。
解析:,所以,=
3.底面半径为1,母线长为3的圆锥的体积是 .
答案:
考点:圆锥的几何结构,体积计算。
解析:圆锥的高为h=,
圆锥的体积V==
4.某学校选修网球课程的学生中,高一、高二、高三年级分别有50名、40名、40名.现用分层抽样的方法在这130名学生中抽取一个样本,已知在高二年级学生中抽取了8名,则在高一年级学生中应抽取的人数为 .
答案:10
考点:分层抽样方法。
解析:设高一抽取x人,则,解得:x=10
5.根据如图所示的伪代码,已知输出值y为3,则输入值x为 .
答案:-2
考点:算法初步。
解析:y=sinx不可能等于3,所以,y=x2-1=3,又x<0,所以,x=-2。
6.甲乙两人各有三张卡片,甲的卡片分别标有数字1、2、3,乙的卡片分别标有数字0、1、3.两人各自随机抽出一张,甲抽出卡片的数字记为a,乙抽出卡片的数字记为b,则a与b的积为奇数的概率为 .
答案:
考点:古典概型。
解析:设甲乙抽出的卡片为(a,b),则所有可能为:
(1,0),(1,1),(1,3),(2,0),(2,1),(2,3),(3,0),(3,1),(3,3),共9种,
积为奇数的有:(1,1),(1,3),(3,1),(3,3),共4种,
所以,所示概率为:
7.若直线l1:与l2:平行,则两平行直线l1,l2间的距离为 .
答案:
考点:直线平行的性质,两平行线之间的距离。
解析:因为两直线平行,所以,,解得:m=2
在直线上取一点(0,2),到直线l2:的距离为:
d==
8.已知等比数列的前n项和为,若,,则= .
答案:1
考点:等比数列的前n项和,通项公式。
解析:,解得:q=2,=1
9.已知双曲线(a>0,b>0)的一条渐近线方程为,则该双曲线的离心率为 .
答案:
考点:双曲线的性质。
解析:的渐近线为:,
所以,,离心率为:e=
10.已知直线l:与圆C:相交于P,Q两点,则= .
答案:0
考点:圆的标准方程,平面向量。
解析:C(2,1),
,解得:或,
即P(2,2),Q(3,1)
=(0,1)(1,0)=0
11.已知正实数x,y满足,若恒成立,则实数m的取值范围为
.
答案:
考点:函数恒成立问题,基本不等式。
解析:恒成立,,
由,得,因为x,y是正实数,所以,y>0,x>4,
=,
所以,
12.设a,b是非零实数,且满足,则= .
答案:
考点:三角恒等变换。
解析:=,
,所以,=
13.已知函数有且仅有三个零点,并且这三个零点构成等差数列,则实数a的值为 .
答案:或
考点:函数的零点,数形结合法,等差数列。
解析:由=0,得:,
原函数有三个零点,即两函数:,有且仅有三个零点,设三个零点为,且,
(1)如下图所示,
,解得:,
又三个零点构成等差数列,则,得,
,解得:;;
(2)如下图所示,
,解得:,由,得,
,消去y,得:,
由韦达定理,得:,且,
,即,化为:,
,,所以,
综上,可得:a的值为或。
14.若存在正实数x,y,z满足,且,则的最小值为
.
答案:
考点:函数的导数及其应用,一元二次不等式,对数运算,计算能力。
解析:由,得,解得:,即,
由,得,即,
令,得,则=0,得:t=,
当t∈时,递减,当t∈时,递增,
当t=时,有唯一的极小值,即最小值:
,所以,的最小值为
二、解答题(本大题共6小题,共计90分.请在答题纸指定区域内作答,解答应写出文字说明,证明过程或演算步骤.)
15.(本题满分14分)
已知函数,.
(1)求函数的单调增区间;
(2)求方程在(0,]内的所有解.
16.(本题满分14分)
如图所示,在三棱柱ABC—A1B1C1中,四边形AA1B1B为矩形,平面AA1B1B⊥平面ABC,点E,F分别是侧面AA1B1B,BB1C1C对角线的交点.
(1)求证:EF∥平面ABC;
(2)BB1⊥AC.
17.(本题满分14分)
为了美化环境,某公园欲将一块空地规划建成休闲草坪,休闲草坪的形状为如图所示的四边形ABCD.其中AB=3百米,AD=百米,且△BCD是以D为直角顶点的等腰直角三角形.拟修建两条小路AC,BD(路的宽度忽略不计),设∠BAD=,(,).
(1)当cos=时,求小路AC的长度;
(2)当草坪ABCD的面积最大时,求此时小路BD的长度.
18.(本题满分16分)
在平面直角坐标系中,椭圆M:(a>b>0)的离心率为,左右顶点分別为A,B,线段AB的长为4.P在椭圆M上且位于第一象限,过点A,B分别作l1⊥PA,l2⊥PB,直线l1,l2交于点C.
(1)若点C的横坐标为﹣1,求P点的坐标;
(2)直线l1与椭圆M的另一交点为Q,且,求的取值范围.
19.(本题满分16分)
已知函数,.(e是自然对数的底数,e≈2.718…)
(1)求函数的极值;
(2)若函数在区间[1,2]上单调递增,求a的取值范围;
(3)若函数在区间(0,)上既存在极大值又存在极小值,并且的极大值小于整数b,求b的最小值.
20.(本题满分16分)
记无穷数列的前n项中最大值为,最小值为,令,数列的前n项和为,数列的前n项和为.
(1)若数列是首项为2,公比为2的等比数列,求;
(2)若数列是等差数列,试问数列是否也一定是等差数列?若是,请证明;若不是,请举例说明;
(3)若,求.
第一部分(附加题)
21.(本题满分10分)
已知矩阵A= ,满足A=,求矩阵A的特征值.
22.(本题满分10分)
在直角坐标系xOy中,直线l的参数方程为(t为参数).在极坐标系中(与直角坐标系xOy取相同的长度单位,且以原点O为极点,极轴与x轴的非负半轴重合),圆C的方程为,求直线l被圆C截得的弦长.
23.(本题满分10分)
将边长为2的正方形ABCD沿对角线BD折叠,使得平面ABD⊥平面CBD,又AE⊥平面ABD.
(1)若AE=,求直线DE与直线BC所成角;
(2)若二面角A—BE—D的大小为,求AE的长度.
24.(本题满分10分)
已知直线x=﹣2上有一动点Q,过点Q作直线l,垂直于y轴,动点P在l1上,且满足(O为坐标原点),记点P的轨迹为C.
(1)求曲线C的方程;
(2)已知定点M(,0),N(,0),点A为曲线C上一点,直线AM交曲线C于另一点B,且点A在线段MB上,直线AN交曲线C于另一点D,求△MBD的内切圆半径r的取值范围.
扬州市2018—2019学年度第一学期期末检测试题
高 三 数 学 参 考 答 案
2019.1
第 一 部 分
1. 2. 3. 4.10 5. 6. 7. 8.1 9.
10.0 11. 12. 13.或 14.
15.解: …………4分
(1)由,解得:
∴函数的单调增区间为 …………8分
(2)由得,解得:,即
∵ ∴或. …………14分
16.证明:(1)∵三棱柱 ∴四边形,四边形均为平行四边形
∵分别是侧面,对角线的交点 ∴分别是,的中点
∴ ………………4分
∵平面,平面∴平面 ………………8分
(2)∵四边形为矩形 ∴
∵平面平面,平面,平面平面
∴平面 ………………12分
∵平面 ∴ ………………14分
17.解:(1)在中,由,
得,又,∴. ………………2分
∵ ∴
由得:,解得:,
∵是以为直角顶点的等腰直角三角形 ∴且
∴ ………………5分
在中,,
解得: ………………7分
(2)由(1)得:,
,此时,且…………10分
当时,四边形的面积最大,即,此时
∴,即 …………13分
答:当时,小路的长度为百米;草坪的面积最大时,小路的长度为百米.
…………14分
18.解:由题意得,解得,∴
∴椭圆M的方程是且 …………3分
(1)方法一:设,,∵ ∴直线AC的方程为,
同理:直线BC的方程为.
联立方程,解得,又∵,
∴点C的坐标为, …………6分
∵点的横坐标为 ∴,又∵P为椭圆上第一象限内一点 ∴
∴点的坐标为. …………8分
(2)设 ∵ ∴,解得:
∵点在椭圆上 ∴ 又
整理得:,解得:或 …………14分
∵P为椭圆上第一象限内一点 ∴,解得: …………16分
方法二:(1)设的斜率为,, ∵P为椭圆上第一象限内一点 ∴
∵ ∴的斜率为.
联立方程,解得,即
∵,∴,则AC的方程为
∵,∴,则BC的方程为.
由,得,即 …………6分
∵点的横坐标为 ∴,解得:
∵ ∴ ∴点的坐标为. …………8分
(2)设,,又直线AC的方程为:
联立方程,得 ∴,解得:
∵ ∴, …………14分
∵ ∴ …………16分
19.解:(1),,令,解得,列表:
极大值
∴当时,函数取得极大值,无极小值 …………3分
(2)由,得
∵,令,
∴函数在区间上单调递增等价于对任意的,函数恒成立
∴,解得. …………8分
(3),
令,
∵在上既存在极大值又存在极小值,∴在上有两个不等实根,
即在上有两个不等实根. …………10分
∵
∴当时,,单调递增,当时,,单调递减
则,∴,解得,∴
∵在上连续且
∴在和上各有一个实根
∴函数在上既存在极大值又存在极小值时,有,并且在区间上存在极小值,在区间上存在极大值.
∴,且
, …………13分
令,当时,,单调递减
∵,∴,即,则
∵的极大值小于整数,∴满足题意的整数的最小值为. …………16分
20.解:(1)∵数列是首项为2,公比为2的等比数列,∴,∴,
则,∴ …………4分
(2)方法(一)若数列是等差数列,设其公差为
∵
根据的定义,有以下结论:
,,且两个不等式中至少有一个取等号, …………6分
①若,则必有,∴,即对,都有
∴,,
∴,即为等差数列;
②当时,则必有,所以,即对,都有
∴,,
所以,即为等差数列;
③当,
∵,中必有一个为0,∴根据上式,一个为0,则另一个亦为0,
即,,∴为常数数列,所以为等差数列,
综上,数列也一定是等差数列. …………10分
方法(二)若数列是等差数列,设通项公式为,则.
对于数列:,增加时,有下列情况:
①若时,则,此时,∴对恒成立
则,,∴
即为常数,则数列是等差数列. …………7分
②若时,则, ∴
∵数列是等差数列且 ∴,
∴ ∴,即,即为常数数列 ∴数列是公差为0的等差数列.
③若时,则,此时,∴对恒成立
则,,∴
即为常数,则数列是等差数列. …………10分
(3)∵,
∴当时,,即,当时,,即.
以下证明:,
当时,
若,则,,所以,不合题意;
若,则,,则,得:,与矛盾,不合题意;
∴,即;
同理可证:,即时,.
①当时,, ∴ ∴,
∵ ∴
∴ …………13分
②当时,,且
∴,则为或.若为,则为常数,与题意不符
∴ ∴ ∴
∴
∴. …………16分
第二部分(加试部分)
21.(B)解:∵ ∴ …………5分
矩阵A的特征多项式为,
令,解得矩阵的特征值为或. …………10分
21.(C)解:将直线的参数方程为化为方程: …………2分
圆的方程为化为直角坐标系方程:,
即,,其圆心,半径为 …………5分
∴圆心到直线的距离为
∴直线被圆截得的弦长为. …………10分
22.解:∵正方形边长为2 ∴,,
又⊥平面
∴以点为原点,所在直线为轴建立空间直角坐标系.
作,垂足为
∵平面⊥平面,平面,平面平面
∴平面
∵ ∴点为的中点, …………2分
(1)∵
∴,,,,
∴ ∴
∴ ∴直线与直线所成角为; …………5分
(2)设的长度为,则
∵⊥平面 ∴平面的一个法向量为 …………6分
设平面的法向量为,又
∴ ∴,解得:,取,则
∴平面的一个法向量为 …………8分
∴
∵二面角的大小为 ∴,解得:
∴的长度为. …………10分
23.解:(1)设点,则 ∴
∵ ∴,即 …………2分
(2)设,直线与轴交点为,内切圆与的切点为.
设直线的方程为:,则联立方程,得:
∴且 ∴ ∴直线的方程为:,
与方程联立得:,化简得:
解得:或 ∵ ∴轴
设的内切圆圆心为,则在轴上且 ……5分
方法(一)∴,且的周长为:
∴
∴ ……8分
方法(二)设,直线的方程为:,其中
直线的方程为:,即,且点与点在直线的同侧
∴,解得:…8分
方法(三)∵ ∴,即,解得:
…8分
令,则
∴在上单调增,则,即的取值范围为. ……10分
同课章节目录
