2018年人教新版五年级上学期《第7章 数学广角--植树问题》单元测试卷(解析版)
文档属性
| 名称 | 2018年人教新版五年级上学期《第7章 数学广角--植树问题》单元测试卷(解析版) |  | |
| 格式 | zip | ||
| 文件大小 | 107.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-01-27 11:51:23 | ||
图片预览


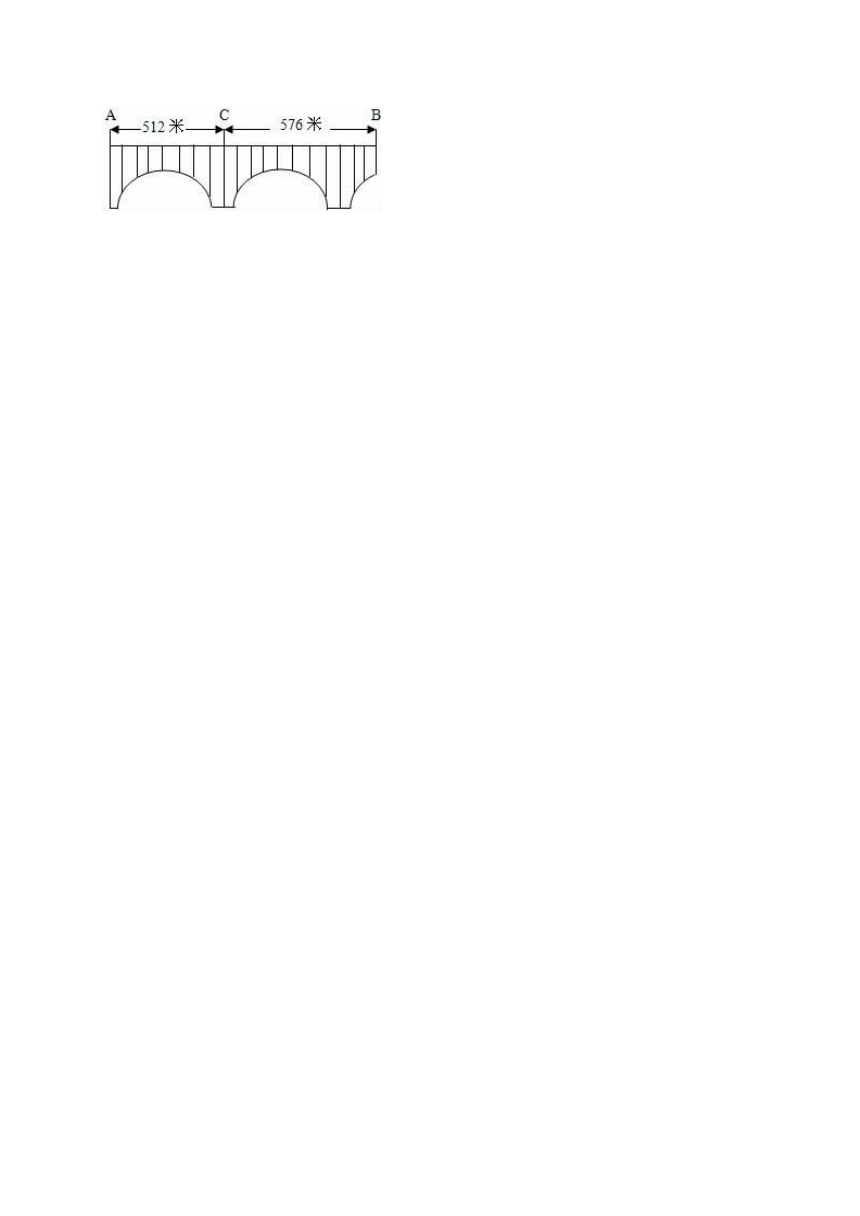


文档简介
2018年人教新版五年级上学期《第7章 数学广角--植树问题》单元测试卷
一.选择题(共5小题)
1.一条10米长的直道的一边,每隔2米放了一盆花,一共要放6盆花.正确的放法是( )
A.两端都放 B.只放一端 C.两端都不放
2.16个小朋友排成一行,每两个小朋友之间间隔2米.第一个小朋友到最后一个小朋友相距( )米.
A.28 B.30 C.32 D.34
3.百货商场的电梯,从1楼到3楼用了6秒.照这样计算,电梯从1楼到10楼要用( )秒.
A.20 B.27 C.30
4.一个圆形花坛周围每隔2米摆一盆花,一共摆了28盆,花坛的周长是( )
A.52 B.54 C.56 D.58
5.把一根木条锯成9段,平均锯一段所用的时间是锯完整根木条所用时间的( )
A. B. C. D.
二.填空题(共14小题)
6.阳阳从1楼到3楼用了12秒,他从一楼到六楼需要 秒.
7.一圆形水池,直径为30米,沿着池边每隔5米栽一棵树,最多能栽 棵.
8.把一根木料锯7次,能锯成 段;要把一根木料锯成9段,要锯 次.
9.在一条马路的一边,每隔30米有一盏路灯,连着马路的两端一共有50盏路灯.这条马路长 米.
10.10位小朋友站成一列做操,每相邻两位小朋友相隔2米,做操的队伍长 米.
11.小力家住在6楼,他从一楼到三楼要2分钟,那么从一楼到六楼要4分钟. .(判断对错)
12.一根木头长10米,要把它平均分成5段.每锯下一段需要8分钟,锯完一共要花 分钟.
13.学校有一条长60米的小道,计划在道路一旁栽树,每隔3米栽一棵,有 个间隔.如果两端都各栽一棵树,那么共需 棵树苗;如果两端都不栽树,那么共需 棵树苗;如果只有一端栽树,那么共需 棵树苗.
14.如果相邻两个同学相隔2米排成长18米一排的队伍做操,那么一共有 个同学.
15.把一根木材锯成3段要4分钟,锯成6段要 分钟.
16.一幢楼房20层高,相邻两层有15级台阶,某人从1层到20层,要走 级台阶.
17.某人到十层大楼的第七层办事,不巧停电,电梯停开.如果从一层走到四层要48秒,那么以同样的速度往上走到七层,还需要 秒才能到达.
18.两栋楼之间每隔2米种一棵树,共种了15棵,这两栋楼之间相距 米.
19.2008年5月26日奥运圣火在扬州境内传递,为了美化环境,需要在每两棵绿树之间布置花卉盆景,每个盆景需要50盆花,已知文昌中路两旁共有208棵绿树,那么共需要 盆花卉.
三.应用题(共2小题)
20.挂钟几点敲几下,敲四点时用了六秒,敲十二点时要用多少秒?
21.多多参加冬季长跑比赛,从出发开始每隔500米设一个服务站(出发点也有一个),当多多看到第5个服务站时,他跑了多少米?
四.解答题(共4小题)
22.学校六一庆祝会上,在一个长9m、宽3m的长方形舞台外沿,每隔1m挂一束气球(一束气球有3个),靠墙的一面不挂,但四个角都要挂.一共需要多少个气球
23.一条大街上一边原有路灯201盏,相邻两盏路灯相距50米;现在换新路灯增加了50盏,相邻两盏路灯的距离是多少米?
24.一条走廊长24米,每隔3米放一盆花,走廊两端都要放.一共要放多少盆花?
25.某地新建一座大桥,在桥面两侧等距离安装照明灯,要求在A、B、C处及AC和BC的中点都要有一盏灯,这样至少需要安装多少盏灯?
2018年人教新版五年级上学期《第7章 数学广角--植树问题》单元测试卷
参考答案与试题解析
一.选择题(共5小题)
1.一条10米长的直道的一边,每隔2米放了一盆花,一共要放6盆花.正确的放法是( )
A.两端都放 B.只放一端 C.两端都不放
【分析】根据题干分析可得,这个直道一共有10÷2=5个间隔,一共放了5+1=6盆花,根据植树问题中两端都要栽的情况可知,此题应属于两端都要栽的情况.
【解答】解:间隔数是:10÷2=5,
6=5+1,
所以正确的放法是两端都要放.
故选:A.
【点评】抓住两端都要栽时:植树棵数=间隔数+1,即可解答.
2.16个小朋友排成一行,每两个小朋友之间间隔2米.第一个小朋友到最后一个小朋友相距( )米.
A.28 B.30 C.32 D.34
【分析】要求第一个小朋友到最后一 个小朋友之间的距离,那么16个小朋友排成一行,也就是有15个间隔;用每个间隔的长度2米,乘上间隔数就是总长度.
【解答】解:(16﹣1)×2,
=15×2,
=30(米);
答:第一个小朋友到最后一 个小朋友相距30米.
故选:B.
【点评】本题属于两端都栽的类型,间隔数比总棵数少1.
3.百货商场的电梯,从1楼到3楼用了6秒.照这样计算,电梯从1楼到10楼要用( )秒.
A.20 B.27 C.30
【分析】从一楼走到三楼用了6秒是指走了(3﹣1)个楼层用了6秒,由此求出走一个楼层所用的时间;再由他从1楼走到10楼知道是走了(10﹣1)个楼层间隔,进而求出答案.
【解答】解:6÷(3﹣1)
=6÷2
=3(秒)
3×(10﹣1)
=3×9
=27(秒)
答:电梯从1楼走到10楼要用27秒.
故选:B.
【点评】本题考查了植树问题,求出走一个楼层所用的时间是本题的关键,另外注意楼层数等于所走的楼数的差.
4.一个圆形花坛周围每隔2米摆一盆花,一共摆了28盆,花坛的周长是( )
A.52 B.54 C.56 D.58
【分析】围成圆圈摆花盆时,花盆数=间隔数,所以这里一共有35个间隔,每个间隔的长度是2米,根据乘法的意义即可解答.
【解答】解:28×2=56(米)
答:这个花坛的周长是56米.
故选:C.
【点评】此题属于植树问题中的围成圆圈植树时:抓住间隔数=植树棵数,即可解答.
5.把一根木条锯成9段,平均锯一段所用的时间是锯完整根木条所用时间的( )
A. B. C. D.
【分析】把一根木条锯成9段,锯了9﹣1=8次,求锯下一段所用的时间是锯成9段所用时间的几分之几,就是求一次是8次的几分之几,求的是分率;用除法计算.
【解答】解:1÷(9﹣1)
=1÷8
=
答:平均锯一段所用的时间是锯完整根木条所用时间的.
故选:A.
【点评】解决此题关键是弄清求得是具体的数量还是分率,求具体的数量平均分的是具体的数量;求分率平均分的是单位“1”;注意锯的次数=段数﹣1.
二.填空题(共14小题)
6.阳阳从1楼到3楼用了12秒,他从一楼到六楼需要 30 秒.
【分析】从1楼到3楼一共走了3﹣1=2个楼梯,用了12秒,所以走一个楼梯需要12÷2=6秒,从一楼到六楼需要走6﹣1=5个楼梯,由此利用乘法的意义即可解答.
【解答】解:12÷(3﹣1)×(6﹣1),
=12÷2×5,
=30(秒),
答:需要30秒.
故答案为:30.
【点评】抓住爬楼问题中:楼层数﹣1=楼梯数,即可解决此类问题.
7.一圆形水池,直径为30米,沿着池边每隔5米栽一棵树,最多能栽 18 棵.
【分析】此题首先应算出圆形水池周长,圆的周长=π×d=3.14×30=94.2(米),再求能栽多少棵树.
【解答】解:①C=π×d,
=3.14×30,
=94.2(米).
②94.2÷5=18.84≈18(棵).
故答案为:18.
【点评】此题考查学生对圆的周长公式的运用,以及去尾法的掌握.
8.把一根木料锯7次,能锯成 8 段;要把一根木料锯成9段,要锯 8 次.
【分析】根据段数=次数+1,求出锯7次用的段数,然后再根据锯的次数=段数﹣1解答即可.
【解答】解:7+1=8(段)
9﹣1=8(次).
故答案为:8;8.
【点评】本题的关键是理解锯的次数=段数﹣1.
9.在一条马路的一边,每隔30米有一盏路灯,连着马路的两端一共有50盏路灯.这条马路长 1470 米.
【分析】因为两端都装路灯,所以间隔数等于灯的盏数﹣1,马路的一边装路灯的间隔数是:50﹣1=49个,由于间距是30米,根据“路的长度=间距×间隔数”可列式为:49×30=1470(米);据此解答.
【解答】解:(50﹣1)×30
=49×30
=1470(米)
答:这条马路有1470米长.
故答案为:1470.
【点评】本题考查了植树问题,知识点是:间隔数=灯的盏数﹣1;知识链接(沿直线上栽):栽树的棵数=间隔数﹣1(两端都不栽),植树的棵数=间隔数+1(两端都栽),植树的棵数=间隔数(只栽一端).
10.10位小朋友站成一列做操,每相邻两位小朋友相隔2米,做操的队伍长 18 米.
【分析】把10个小朋友看作10棵树,那么这就是植树问题中的两端都要栽的情况,1个间隔长度为2米,只要求出有几个间隔即可:间隔数=植树棵数﹣1,由此即可解决问题.
【解答】解:(10﹣1)×2,
=9×2,
=18(米),
答:做操的队伍长18米.
故答案为:18.
【点评】此题可以归属在植树问题中的两端都要栽的情况,只要求出间隔数问题即可解决.
11.小力家住在6楼,他从一楼到三楼要2分钟,那么从一楼到六楼要4分钟. × .(判断对错)
【分析】从一楼到三楼,向上爬了3﹣1=2层,向上每爬1层用2÷2=1分钟,从一楼到六楼,向上爬了6﹣1=5层,共用5×1=5分钟.
【解答】解:(3﹣1)÷2,
=2÷2,
=1(分钟);
1×(6﹣1),
=1×5,
=5(分钟);
答:从一楼到六楼要用5分钟.
故答案为:×.
【点评】对于这类题目,注意向上爬的层数比楼数少1,即可算出所用的时间.
12.一根木头长10米,要把它平均分成5段.每锯下一段需要8分钟,锯完一共要花 32 分钟.
【分析】平均分成5段,需要锯5﹣1=4次,由此即可解答.
【解答】解:(5﹣1)×8,
=4×8,
=32(分钟),
答:锯完一共要花32分钟.
故答案为:32.
【点评】锯的次数=段数﹣1,此题与木头的长度无关.
13.学校有一条长60米的小道,计划在道路一旁栽树,每隔3米栽一棵,有 20 个间隔.如果两端都各栽一棵树,那么共需 21 棵树苗;如果两端都不栽树,那么共需 19 棵树苗;如果只有一端栽树,那么共需 20 棵树苗.
【分析】在60米的小道一旁栽树,每隔3米栽一棵,则间隔数有60÷3个;两端都要栽时,植树棵数=间隔数+1;两端都不栽时,植树棵数=间隔数﹣1;只有一端栽时,植树棵数=间隔数;据此即可解答问题.
【解答】解:(1)60÷3=20,
(2)20+1=21(棵),
(3)20﹣1=19(棵),
(4)只有一端栽时,共需要20棵树苗;
答:每隔3米栽一棵,有20个间隔.如果两端都各栽一棵树,那么共需21棵树苗;如果两端都不栽树,那么共需19棵树苗;如果只有一端栽树,那么共需20棵树苗.
故答案为:20,21,19,20.
【点评】此题主要考查植树问题中的三种不同的情况,关键是求出间隔数.
14.如果相邻两个同学相隔2米排成长18米一排的队伍做操,那么一共有 10 个同学.
【分析】先用18除以2求出间隔数,再加1就是一共有同学的个数.
【解答】解:18÷2+1=10(个),
答:一共有10个同学,
故答案为:10.
【点评】此题属于两侧都植树的问题,所以要求的同学的个数=间隔数+1.
15.把一根木材锯成3段要4分钟,锯成6段要 10 分钟.
【分析】锯成3段需要锯2次,由此可以求出锯一次需要的时间,锯成6段需要锯5次,用每次锯的时间乘上5,就是需要的总时间.
【解答】解:4÷(3﹣1)×(6﹣1)
=4÷2×5
=10(分钟)
答:锯成6段要10分钟.
故答案为:10.
【点评】本题考查了植树问题:锯1次就可以锯成2段,存在这个关系:锯的次数=锯成的段数﹣1.
16.一幢楼房20层高,相邻两层有15级台阶,某人从1层到20层,要走 285 级台阶.
【分析】从1到20层,共走了20﹣1=19层,所以要走19×15=285级台阶.
【解答】解:15×(20﹣1),
=15×19,
=285(级).
答:要走285级台阶.
故答案为:285.
【点评】解答此类问题的关键是要弄清第一层楼没有台阶,搞清这个问题就能正确解答.
17.某人到十层大楼的第七层办事,不巧停电,电梯停开.如果从一层走到四层要48秒,那么以同样的速度往上走到七层,还需要 48 秒才能到达.
【分析】“从一层走到四层”,实际上是爬了3层楼梯,共需要48秒,从四楼走到七楼又需要爬7﹣4=3层楼梯,所以还需要48秒,由此即可解答.
【解答】解:“从一层走到四层”,实际上是爬了3层楼梯,共需要48秒,
从四楼走到七楼又需要爬7﹣4=3层楼梯,所以还需要48秒,
故答案为:48.
【点评】爬的层数=楼层数之差,由此即可解答此类问题.
18.两栋楼之间每隔2米种一棵树,共种了15棵,这两栋楼之间相距 32 米.
【分析】两栋楼之间植树,由于树的两端都是楼房,树和楼之间各有一个间隔,那么间隔数=植树棵数+1,由此求出间隔数,再用每个间隔的长度乘上间隔数,就是两栋楼之间的距离.
【解答】解:2×(15+1)
=2×16
=32(米)
答:这两栋楼之间相距32米.
故答案为:32.
【点评】解决本题要注意树和两侧的楼之间各有1个间隔,那么间隔数比树的棵数多1.
19.2008年5月26日奥运圣火在扬州境内传递,为了美化环境,需要在每两棵绿树之间布置花卉盆景,每个盆景需要50盆花,已知文昌中路两旁共有208棵绿树,那么共需要 10300 盆花卉.
【分析】根据题意,可知道路两旁共有树208棵,那么一旁的棵数就是208÷2=104(棵),可以求出一旁树与树之间的间隔数是104﹣1=103(个),根据题意可知在每两棵绿树之间布置花卉盆景,每个盆景需要50盆花,可以求出一旁的花卉盆数,再乘上2就是文昌中路两旁共需要的花卉盆数.
【解答】解:根据题意可得文昌中路一旁的绿树棵数是:208÷2=104(棵),
那么这一旁的树与树之间的间隔数是:104﹣1=103(个),
由题意可得一旁需要的花卉盆数是:103×50=5150(盆),
那么文昌中路两旁需要的花卉盆数是:5150×2=10300(盆).
故填:10300.
【点评】由题意可知208棵是道路两旁的棵数,先求出道路一旁的棵数,这是这道题的关键,再根据题目给出的条件和问题进一步解答即可.
三.应用题(共2小题)
20.挂钟几点敲几下,敲四点时用了六秒,敲十二点时要用多少秒?
【分析】挂钟4点钟敲4下,6秒敲完,有4﹣1=3个间隔,每个间隔是6÷3=2秒,因此12点钟敲12下,有12﹣1=11个间隔,即11×2=22秒.
【解答】解:6÷(4﹣1)×(12﹣1)
=6÷3×11
=22(秒)
答:敲十二点时要用22秒.
【点评】对于这类题目,根据敲铃的下数,可知道其间隔数,间隔数比下数少1,即可计算出敲完的时间.
21.多多参加冬季长跑比赛,从出发开始每隔500米设一个服务站(出发点也有一个),当多多看到第5个服务站时,他跑了多少米?
【分析】因为从起点开始设服务站,所以当多多跑到第5个服务站时,实际上跑了(5﹣1)个间隔的距离,由此根据整数乘法的意义,用间距500乘间隔数4解答即可.
【解答】解:500×(5﹣1)
=500×4
=2000(米)
答:他跑了2000米.
【点评】本题属于植树问题中的两端都栽的情况:植树的棵数﹣1=间隔数.
四.解答题(共4小题)
22.学校六一庆祝会上,在一个长9m、宽3m的长方形舞台外沿,每隔1m挂一束气球(一束气球有3个),靠墙的一面不挂,但四个角都要挂.一共需要多少个气球
【分析】由于靠墙的一面不挂,但四个角都要挂,所以此题可看作是两端都植的植树问题,全长是9+3+3=15米,用15÷1求得间隔数,再加上1就是气球的束数,再乘3就是需要的气球总个数;据此解答.
【解答】解:(9+3+3)÷1+1
=15÷1+1
=15+1
=16(束)
16×3=48(个)
答:一共需要48个气球.
【点评】解题关键是明确属于两端都植的植树问题,植树棵数=间隔数+1.
23.一条大街上一边原有路灯201盏,相邻两盏路灯相距50米;现在换新路灯增加了50盏,相邻两盏路灯的距离是多少米?
【分析】先利用原有的路灯盏数和间隔长度,求出这条大街的总长度是(201﹣1)×50=10000(米),换新路灯后,一共有路灯201+50=251盏,此时的间隔数是251﹣1=250,由此即可求出1个间隔的长度是10000÷250=40(米).
【解答】解:(201﹣1)×50÷(201+50﹣1)
=200×50÷250
=40(米)
答:相邻的两盏路灯的距离是40米.
【点评】解答此题的关键是抓住:间隔数=路灯盏数﹣1.
24.一条走廊长24米,每隔3米放一盆花,走廊两端都要放.一共要放多少盆花?
【分析】用24÷3求出24里面有几个3,再根据“走廊两端都要放.”所以再加1后就是一共放花的盆数.
【解答】解:24÷3+1,
=8+1,
=9(盆),
答:一共要放9盆花.
【点评】抓住两端都要放花的情况:放花的盆数=间隔数+1.代入数据即可解答.
25.某地新建一座大桥,在桥面两侧等距离安装照明灯,要求在A、B、C处及AC和BC的中点都要有一盏灯,这样至少需要安装多少盏灯?
【分析】要在A、B、C处及AC和BC的中点都要有一盏灯,这五个点到桥头的距离必须是灯距的倍数;AC的中间距是512÷2=256米;BC的中间距是576÷2=288米;要求至少需要安装多少盏灯,就必须使灯距最大,也就是求256和288的最大公约数,然后用(512+576)除以最大公约数再加1,即是每边的盏数,然后再乘2即可求出两边一共安装的盏数.
【解答】解:512÷2=256(米),
576÷2=288(米);
256=2×2×2×2×2×2×2×2,
288=2×2×2×2×2×3×3,
256和288的最大公约数是:2×2×2×2×2=32,
所以灯距最大是32米;
(512+576)÷32+1,
=34+1,
=35(盏);
35×2=70(盏);
答:至少需要安装70盏灯.
【点评】本题是植树问题在实际生活中的应用,根据两个中间距确定灯距是本题的关键,注意:盏数=距离÷灯距+1,不要忘记加“1”.
一.选择题(共5小题)
1.一条10米长的直道的一边,每隔2米放了一盆花,一共要放6盆花.正确的放法是( )
A.两端都放 B.只放一端 C.两端都不放
2.16个小朋友排成一行,每两个小朋友之间间隔2米.第一个小朋友到最后一个小朋友相距( )米.
A.28 B.30 C.32 D.34
3.百货商场的电梯,从1楼到3楼用了6秒.照这样计算,电梯从1楼到10楼要用( )秒.
A.20 B.27 C.30
4.一个圆形花坛周围每隔2米摆一盆花,一共摆了28盆,花坛的周长是( )
A.52 B.54 C.56 D.58
5.把一根木条锯成9段,平均锯一段所用的时间是锯完整根木条所用时间的( )
A. B. C. D.
二.填空题(共14小题)
6.阳阳从1楼到3楼用了12秒,他从一楼到六楼需要 秒.
7.一圆形水池,直径为30米,沿着池边每隔5米栽一棵树,最多能栽 棵.
8.把一根木料锯7次,能锯成 段;要把一根木料锯成9段,要锯 次.
9.在一条马路的一边,每隔30米有一盏路灯,连着马路的两端一共有50盏路灯.这条马路长 米.
10.10位小朋友站成一列做操,每相邻两位小朋友相隔2米,做操的队伍长 米.
11.小力家住在6楼,他从一楼到三楼要2分钟,那么从一楼到六楼要4分钟. .(判断对错)
12.一根木头长10米,要把它平均分成5段.每锯下一段需要8分钟,锯完一共要花 分钟.
13.学校有一条长60米的小道,计划在道路一旁栽树,每隔3米栽一棵,有 个间隔.如果两端都各栽一棵树,那么共需 棵树苗;如果两端都不栽树,那么共需 棵树苗;如果只有一端栽树,那么共需 棵树苗.
14.如果相邻两个同学相隔2米排成长18米一排的队伍做操,那么一共有 个同学.
15.把一根木材锯成3段要4分钟,锯成6段要 分钟.
16.一幢楼房20层高,相邻两层有15级台阶,某人从1层到20层,要走 级台阶.
17.某人到十层大楼的第七层办事,不巧停电,电梯停开.如果从一层走到四层要48秒,那么以同样的速度往上走到七层,还需要 秒才能到达.
18.两栋楼之间每隔2米种一棵树,共种了15棵,这两栋楼之间相距 米.
19.2008年5月26日奥运圣火在扬州境内传递,为了美化环境,需要在每两棵绿树之间布置花卉盆景,每个盆景需要50盆花,已知文昌中路两旁共有208棵绿树,那么共需要 盆花卉.
三.应用题(共2小题)
20.挂钟几点敲几下,敲四点时用了六秒,敲十二点时要用多少秒?
21.多多参加冬季长跑比赛,从出发开始每隔500米设一个服务站(出发点也有一个),当多多看到第5个服务站时,他跑了多少米?
四.解答题(共4小题)
22.学校六一庆祝会上,在一个长9m、宽3m的长方形舞台外沿,每隔1m挂一束气球(一束气球有3个),靠墙的一面不挂,但四个角都要挂.一共需要多少个气球
23.一条大街上一边原有路灯201盏,相邻两盏路灯相距50米;现在换新路灯增加了50盏,相邻两盏路灯的距离是多少米?
24.一条走廊长24米,每隔3米放一盆花,走廊两端都要放.一共要放多少盆花?
25.某地新建一座大桥,在桥面两侧等距离安装照明灯,要求在A、B、C处及AC和BC的中点都要有一盏灯,这样至少需要安装多少盏灯?
2018年人教新版五年级上学期《第7章 数学广角--植树问题》单元测试卷
参考答案与试题解析
一.选择题(共5小题)
1.一条10米长的直道的一边,每隔2米放了一盆花,一共要放6盆花.正确的放法是( )
A.两端都放 B.只放一端 C.两端都不放
【分析】根据题干分析可得,这个直道一共有10÷2=5个间隔,一共放了5+1=6盆花,根据植树问题中两端都要栽的情况可知,此题应属于两端都要栽的情况.
【解答】解:间隔数是:10÷2=5,
6=5+1,
所以正确的放法是两端都要放.
故选:A.
【点评】抓住两端都要栽时:植树棵数=间隔数+1,即可解答.
2.16个小朋友排成一行,每两个小朋友之间间隔2米.第一个小朋友到最后一个小朋友相距( )米.
A.28 B.30 C.32 D.34
【分析】要求第一个小朋友到最后一 个小朋友之间的距离,那么16个小朋友排成一行,也就是有15个间隔;用每个间隔的长度2米,乘上间隔数就是总长度.
【解答】解:(16﹣1)×2,
=15×2,
=30(米);
答:第一个小朋友到最后一 个小朋友相距30米.
故选:B.
【点评】本题属于两端都栽的类型,间隔数比总棵数少1.
3.百货商场的电梯,从1楼到3楼用了6秒.照这样计算,电梯从1楼到10楼要用( )秒.
A.20 B.27 C.30
【分析】从一楼走到三楼用了6秒是指走了(3﹣1)个楼层用了6秒,由此求出走一个楼层所用的时间;再由他从1楼走到10楼知道是走了(10﹣1)个楼层间隔,进而求出答案.
【解答】解:6÷(3﹣1)
=6÷2
=3(秒)
3×(10﹣1)
=3×9
=27(秒)
答:电梯从1楼走到10楼要用27秒.
故选:B.
【点评】本题考查了植树问题,求出走一个楼层所用的时间是本题的关键,另外注意楼层数等于所走的楼数的差.
4.一个圆形花坛周围每隔2米摆一盆花,一共摆了28盆,花坛的周长是( )
A.52 B.54 C.56 D.58
【分析】围成圆圈摆花盆时,花盆数=间隔数,所以这里一共有35个间隔,每个间隔的长度是2米,根据乘法的意义即可解答.
【解答】解:28×2=56(米)
答:这个花坛的周长是56米.
故选:C.
【点评】此题属于植树问题中的围成圆圈植树时:抓住间隔数=植树棵数,即可解答.
5.把一根木条锯成9段,平均锯一段所用的时间是锯完整根木条所用时间的( )
A. B. C. D.
【分析】把一根木条锯成9段,锯了9﹣1=8次,求锯下一段所用的时间是锯成9段所用时间的几分之几,就是求一次是8次的几分之几,求的是分率;用除法计算.
【解答】解:1÷(9﹣1)
=1÷8
=
答:平均锯一段所用的时间是锯完整根木条所用时间的.
故选:A.
【点评】解决此题关键是弄清求得是具体的数量还是分率,求具体的数量平均分的是具体的数量;求分率平均分的是单位“1”;注意锯的次数=段数﹣1.
二.填空题(共14小题)
6.阳阳从1楼到3楼用了12秒,他从一楼到六楼需要 30 秒.
【分析】从1楼到3楼一共走了3﹣1=2个楼梯,用了12秒,所以走一个楼梯需要12÷2=6秒,从一楼到六楼需要走6﹣1=5个楼梯,由此利用乘法的意义即可解答.
【解答】解:12÷(3﹣1)×(6﹣1),
=12÷2×5,
=30(秒),
答:需要30秒.
故答案为:30.
【点评】抓住爬楼问题中:楼层数﹣1=楼梯数,即可解决此类问题.
7.一圆形水池,直径为30米,沿着池边每隔5米栽一棵树,最多能栽 18 棵.
【分析】此题首先应算出圆形水池周长,圆的周长=π×d=3.14×30=94.2(米),再求能栽多少棵树.
【解答】解:①C=π×d,
=3.14×30,
=94.2(米).
②94.2÷5=18.84≈18(棵).
故答案为:18.
【点评】此题考查学生对圆的周长公式的运用,以及去尾法的掌握.
8.把一根木料锯7次,能锯成 8 段;要把一根木料锯成9段,要锯 8 次.
【分析】根据段数=次数+1,求出锯7次用的段数,然后再根据锯的次数=段数﹣1解答即可.
【解答】解:7+1=8(段)
9﹣1=8(次).
故答案为:8;8.
【点评】本题的关键是理解锯的次数=段数﹣1.
9.在一条马路的一边,每隔30米有一盏路灯,连着马路的两端一共有50盏路灯.这条马路长 1470 米.
【分析】因为两端都装路灯,所以间隔数等于灯的盏数﹣1,马路的一边装路灯的间隔数是:50﹣1=49个,由于间距是30米,根据“路的长度=间距×间隔数”可列式为:49×30=1470(米);据此解答.
【解答】解:(50﹣1)×30
=49×30
=1470(米)
答:这条马路有1470米长.
故答案为:1470.
【点评】本题考查了植树问题,知识点是:间隔数=灯的盏数﹣1;知识链接(沿直线上栽):栽树的棵数=间隔数﹣1(两端都不栽),植树的棵数=间隔数+1(两端都栽),植树的棵数=间隔数(只栽一端).
10.10位小朋友站成一列做操,每相邻两位小朋友相隔2米,做操的队伍长 18 米.
【分析】把10个小朋友看作10棵树,那么这就是植树问题中的两端都要栽的情况,1个间隔长度为2米,只要求出有几个间隔即可:间隔数=植树棵数﹣1,由此即可解决问题.
【解答】解:(10﹣1)×2,
=9×2,
=18(米),
答:做操的队伍长18米.
故答案为:18.
【点评】此题可以归属在植树问题中的两端都要栽的情况,只要求出间隔数问题即可解决.
11.小力家住在6楼,他从一楼到三楼要2分钟,那么从一楼到六楼要4分钟. × .(判断对错)
【分析】从一楼到三楼,向上爬了3﹣1=2层,向上每爬1层用2÷2=1分钟,从一楼到六楼,向上爬了6﹣1=5层,共用5×1=5分钟.
【解答】解:(3﹣1)÷2,
=2÷2,
=1(分钟);
1×(6﹣1),
=1×5,
=5(分钟);
答:从一楼到六楼要用5分钟.
故答案为:×.
【点评】对于这类题目,注意向上爬的层数比楼数少1,即可算出所用的时间.
12.一根木头长10米,要把它平均分成5段.每锯下一段需要8分钟,锯完一共要花 32 分钟.
【分析】平均分成5段,需要锯5﹣1=4次,由此即可解答.
【解答】解:(5﹣1)×8,
=4×8,
=32(分钟),
答:锯完一共要花32分钟.
故答案为:32.
【点评】锯的次数=段数﹣1,此题与木头的长度无关.
13.学校有一条长60米的小道,计划在道路一旁栽树,每隔3米栽一棵,有 20 个间隔.如果两端都各栽一棵树,那么共需 21 棵树苗;如果两端都不栽树,那么共需 19 棵树苗;如果只有一端栽树,那么共需 20 棵树苗.
【分析】在60米的小道一旁栽树,每隔3米栽一棵,则间隔数有60÷3个;两端都要栽时,植树棵数=间隔数+1;两端都不栽时,植树棵数=间隔数﹣1;只有一端栽时,植树棵数=间隔数;据此即可解答问题.
【解答】解:(1)60÷3=20,
(2)20+1=21(棵),
(3)20﹣1=19(棵),
(4)只有一端栽时,共需要20棵树苗;
答:每隔3米栽一棵,有20个间隔.如果两端都各栽一棵树,那么共需21棵树苗;如果两端都不栽树,那么共需19棵树苗;如果只有一端栽树,那么共需20棵树苗.
故答案为:20,21,19,20.
【点评】此题主要考查植树问题中的三种不同的情况,关键是求出间隔数.
14.如果相邻两个同学相隔2米排成长18米一排的队伍做操,那么一共有 10 个同学.
【分析】先用18除以2求出间隔数,再加1就是一共有同学的个数.
【解答】解:18÷2+1=10(个),
答:一共有10个同学,
故答案为:10.
【点评】此题属于两侧都植树的问题,所以要求的同学的个数=间隔数+1.
15.把一根木材锯成3段要4分钟,锯成6段要 10 分钟.
【分析】锯成3段需要锯2次,由此可以求出锯一次需要的时间,锯成6段需要锯5次,用每次锯的时间乘上5,就是需要的总时间.
【解答】解:4÷(3﹣1)×(6﹣1)
=4÷2×5
=10(分钟)
答:锯成6段要10分钟.
故答案为:10.
【点评】本题考查了植树问题:锯1次就可以锯成2段,存在这个关系:锯的次数=锯成的段数﹣1.
16.一幢楼房20层高,相邻两层有15级台阶,某人从1层到20层,要走 285 级台阶.
【分析】从1到20层,共走了20﹣1=19层,所以要走19×15=285级台阶.
【解答】解:15×(20﹣1),
=15×19,
=285(级).
答:要走285级台阶.
故答案为:285.
【点评】解答此类问题的关键是要弄清第一层楼没有台阶,搞清这个问题就能正确解答.
17.某人到十层大楼的第七层办事,不巧停电,电梯停开.如果从一层走到四层要48秒,那么以同样的速度往上走到七层,还需要 48 秒才能到达.
【分析】“从一层走到四层”,实际上是爬了3层楼梯,共需要48秒,从四楼走到七楼又需要爬7﹣4=3层楼梯,所以还需要48秒,由此即可解答.
【解答】解:“从一层走到四层”,实际上是爬了3层楼梯,共需要48秒,
从四楼走到七楼又需要爬7﹣4=3层楼梯,所以还需要48秒,
故答案为:48.
【点评】爬的层数=楼层数之差,由此即可解答此类问题.
18.两栋楼之间每隔2米种一棵树,共种了15棵,这两栋楼之间相距 32 米.
【分析】两栋楼之间植树,由于树的两端都是楼房,树和楼之间各有一个间隔,那么间隔数=植树棵数+1,由此求出间隔数,再用每个间隔的长度乘上间隔数,就是两栋楼之间的距离.
【解答】解:2×(15+1)
=2×16
=32(米)
答:这两栋楼之间相距32米.
故答案为:32.
【点评】解决本题要注意树和两侧的楼之间各有1个间隔,那么间隔数比树的棵数多1.
19.2008年5月26日奥运圣火在扬州境内传递,为了美化环境,需要在每两棵绿树之间布置花卉盆景,每个盆景需要50盆花,已知文昌中路两旁共有208棵绿树,那么共需要 10300 盆花卉.
【分析】根据题意,可知道路两旁共有树208棵,那么一旁的棵数就是208÷2=104(棵),可以求出一旁树与树之间的间隔数是104﹣1=103(个),根据题意可知在每两棵绿树之间布置花卉盆景,每个盆景需要50盆花,可以求出一旁的花卉盆数,再乘上2就是文昌中路两旁共需要的花卉盆数.
【解答】解:根据题意可得文昌中路一旁的绿树棵数是:208÷2=104(棵),
那么这一旁的树与树之间的间隔数是:104﹣1=103(个),
由题意可得一旁需要的花卉盆数是:103×50=5150(盆),
那么文昌中路两旁需要的花卉盆数是:5150×2=10300(盆).
故填:10300.
【点评】由题意可知208棵是道路两旁的棵数,先求出道路一旁的棵数,这是这道题的关键,再根据题目给出的条件和问题进一步解答即可.
三.应用题(共2小题)
20.挂钟几点敲几下,敲四点时用了六秒,敲十二点时要用多少秒?
【分析】挂钟4点钟敲4下,6秒敲完,有4﹣1=3个间隔,每个间隔是6÷3=2秒,因此12点钟敲12下,有12﹣1=11个间隔,即11×2=22秒.
【解答】解:6÷(4﹣1)×(12﹣1)
=6÷3×11
=22(秒)
答:敲十二点时要用22秒.
【点评】对于这类题目,根据敲铃的下数,可知道其间隔数,间隔数比下数少1,即可计算出敲完的时间.
21.多多参加冬季长跑比赛,从出发开始每隔500米设一个服务站(出发点也有一个),当多多看到第5个服务站时,他跑了多少米?
【分析】因为从起点开始设服务站,所以当多多跑到第5个服务站时,实际上跑了(5﹣1)个间隔的距离,由此根据整数乘法的意义,用间距500乘间隔数4解答即可.
【解答】解:500×(5﹣1)
=500×4
=2000(米)
答:他跑了2000米.
【点评】本题属于植树问题中的两端都栽的情况:植树的棵数﹣1=间隔数.
四.解答题(共4小题)
22.学校六一庆祝会上,在一个长9m、宽3m的长方形舞台外沿,每隔1m挂一束气球(一束气球有3个),靠墙的一面不挂,但四个角都要挂.一共需要多少个气球
【分析】由于靠墙的一面不挂,但四个角都要挂,所以此题可看作是两端都植的植树问题,全长是9+3+3=15米,用15÷1求得间隔数,再加上1就是气球的束数,再乘3就是需要的气球总个数;据此解答.
【解答】解:(9+3+3)÷1+1
=15÷1+1
=15+1
=16(束)
16×3=48(个)
答:一共需要48个气球.
【点评】解题关键是明确属于两端都植的植树问题,植树棵数=间隔数+1.
23.一条大街上一边原有路灯201盏,相邻两盏路灯相距50米;现在换新路灯增加了50盏,相邻两盏路灯的距离是多少米?
【分析】先利用原有的路灯盏数和间隔长度,求出这条大街的总长度是(201﹣1)×50=10000(米),换新路灯后,一共有路灯201+50=251盏,此时的间隔数是251﹣1=250,由此即可求出1个间隔的长度是10000÷250=40(米).
【解答】解:(201﹣1)×50÷(201+50﹣1)
=200×50÷250
=40(米)
答:相邻的两盏路灯的距离是40米.
【点评】解答此题的关键是抓住:间隔数=路灯盏数﹣1.
24.一条走廊长24米,每隔3米放一盆花,走廊两端都要放.一共要放多少盆花?
【分析】用24÷3求出24里面有几个3,再根据“走廊两端都要放.”所以再加1后就是一共放花的盆数.
【解答】解:24÷3+1,
=8+1,
=9(盆),
答:一共要放9盆花.
【点评】抓住两端都要放花的情况:放花的盆数=间隔数+1.代入数据即可解答.
25.某地新建一座大桥,在桥面两侧等距离安装照明灯,要求在A、B、C处及AC和BC的中点都要有一盏灯,这样至少需要安装多少盏灯?
【分析】要在A、B、C处及AC和BC的中点都要有一盏灯,这五个点到桥头的距离必须是灯距的倍数;AC的中间距是512÷2=256米;BC的中间距是576÷2=288米;要求至少需要安装多少盏灯,就必须使灯距最大,也就是求256和288的最大公约数,然后用(512+576)除以最大公约数再加1,即是每边的盏数,然后再乘2即可求出两边一共安装的盏数.
【解答】解:512÷2=256(米),
576÷2=288(米);
256=2×2×2×2×2×2×2×2,
288=2×2×2×2×2×3×3,
256和288的最大公约数是:2×2×2×2×2=32,
所以灯距最大是32米;
(512+576)÷32+1,
=34+1,
=35(盏);
35×2=70(盏);
答:至少需要安装70盏灯.
【点评】本题是植树问题在实际生活中的应用,根据两个中间距确定灯距是本题的关键,注意:盏数=距离÷灯距+1,不要忘记加“1”.
