江苏省宿迁市2019届高三上学期期末考试数学试题(解析版)
文档属性
| 名称 | 江苏省宿迁市2019届高三上学期期末考试数学试题(解析版) |  | |
| 格式 | zip | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-01-28 16:06:48 | ||
图片预览



文档简介
宿迁市2018~2019学年度第一学期市直高三期末测试
数 学
参考公式:锥体的体积公式 ,其中是锥体的底面面积,是高.
一、填空题:本大题共14小题,每小题5分,共计70分.请把答案填写在答题卡相应位置上.
1. 已知集合,,则 ▲ .
答案:
考点:集合的运算。
解析:,
所以,
2. 已知复数满足(其中i为虚数单位),则的值为 ▲ .
答案:
考点:复数的概念及运算。
解析:,
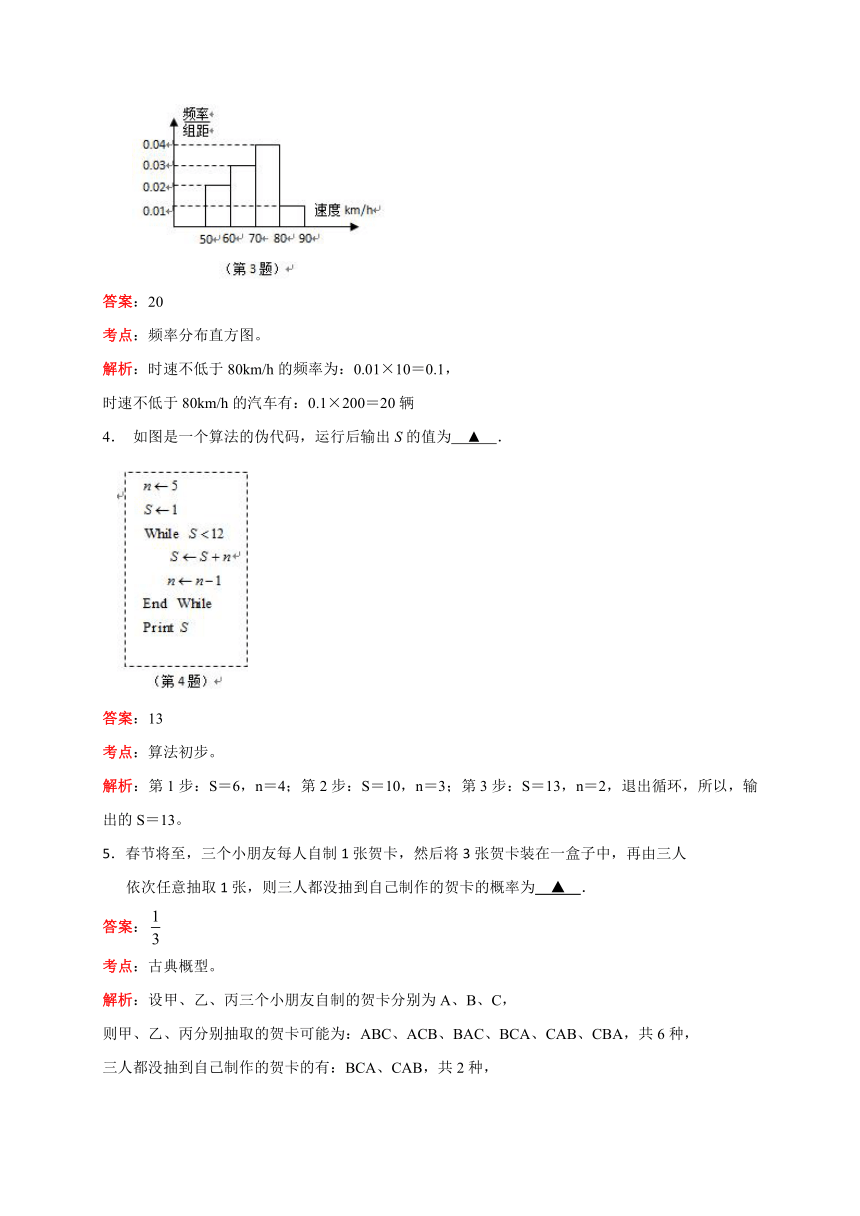
3. 交通部门对某路段公路上行驶的汽车速度实施监控,从速度不小于50km/h的汽车中
抽取200辆汽车进行测速分析,得到如图所示的时速的频率分布直方图,则时速
不低于80km/h的汽车有 ▲ 辆.
答案:20
考点:频率分布直方图。
解析:时速不低于80km/h的频率为:0.01×10=0.1,
时速不低于80km/h的汽车有:0.1×200=20辆
4. 如图是一个算法的伪代码,运行后输出S的值为 ▲ .
答案:13
考点:算法初步。
解析:第1步:S=6,n=4;第2步:S=10,n=3;第3步:S=13,n=2,退出循环,所以,输出的S=13。
5.春节将至,三个小朋友每人自制1张贺卡,然后将3张贺卡装在一盒子中,再由三人
依次任意抽取1张,则三人都没抽到自己制作的贺卡的概率为 ▲ .
答案:
考点:古典概型。
解析:设甲、乙、丙三个小朋友自制的贺卡分别为A、B、C,
则甲、乙、丙分别抽取的贺卡可能为:ABC、ACB、BAC、BCA、CAB、CBA,共6种,
三人都没抽到自己制作的贺卡的有:BCA、CAB,共2种,
所以,所求的概率为:P=
6. 设圆锥的轴截面是一个边长为2cm的正三角形,则该圆锥的体积为 ▲ cm3.
答案:;
考点:圆锥的空间结构及其体积的计算。
解析:圆锥的底面半径R=1,高h==,
圆锥的体积为:V==
7. 已知双曲线的离心率为2,右焦点与抛物线的焦
点重合,则双曲线的顶点到渐近线的距离为 ▲ .
答案:
考点:双曲线、抛物线的性质。
解析:抛物线的焦点为F(4,0),因为双曲线与抛物线的焦点重合,
所以,c=4,离心率e==2,所以,a=2,b=,
双曲线为:,渐近线为:,顶点为(-2,0),(2,0)
双曲线的顶点到渐近线的距离为
8. 已知数列前n项和为,,,则的值为 ▲ .
答案: 1013
考点:等比数列的前n项和,数列的递推公式。
解析:由,得:,即,
所以,数列是以2为首项,2为公比的等比数列,
设的前n项和为Tn,则=1022,
S9=T9-9=1013
9. 已知正实数满足,则的最小值为 ▲ .
答案:
考点:函数的导数及其应用。
解析:由得:>0,所以,0<b<1,
令f(b)==
===,
当b∈(0,)时,f(b)递减,当b∈(,1)时,f(b)递增,
所以,当b=时,f(b)有唯一的极小值,
即是最小值:=
10. 已知点,若圆上存在点M满足,则实数的取值范围是 ▲ .
答案:
考点:动点的轨迹方程,圆的标准方程。
解析:设M(x,y),因为,所以,点M的轨迹方程为:
(-1-x,-y)(1-x,-y)=3,即x2+y2=4,
又因为点M在圆上,
两圆有交点,所以,,
即,解得:
11. 对于函数,如果是偶函数,且其图象上的任意一点都在平面区域
内,则称该函数为“V型函数”.下列函数:①;②;
③; ④.其中是“V型函数”的是 ▲ .(将符合条件
的函数序号都填在横线上).
答案:③④
考点:函数的奇偶性,函数的导数及其应用,阅读新知识解决问题的能力。
解析:①不是偶函数,排除。
②是偶函数,当x>0时,=,不是“V型函数”。
③是偶函数,当x>0时,,令,>0,
f(x)在(0,+∞)是增函数,,即,是“V型函数”。
④是偶函数,当x>0时,,令,
=,当时,,是增函数,
>=0,所以,,是“V型函数”。
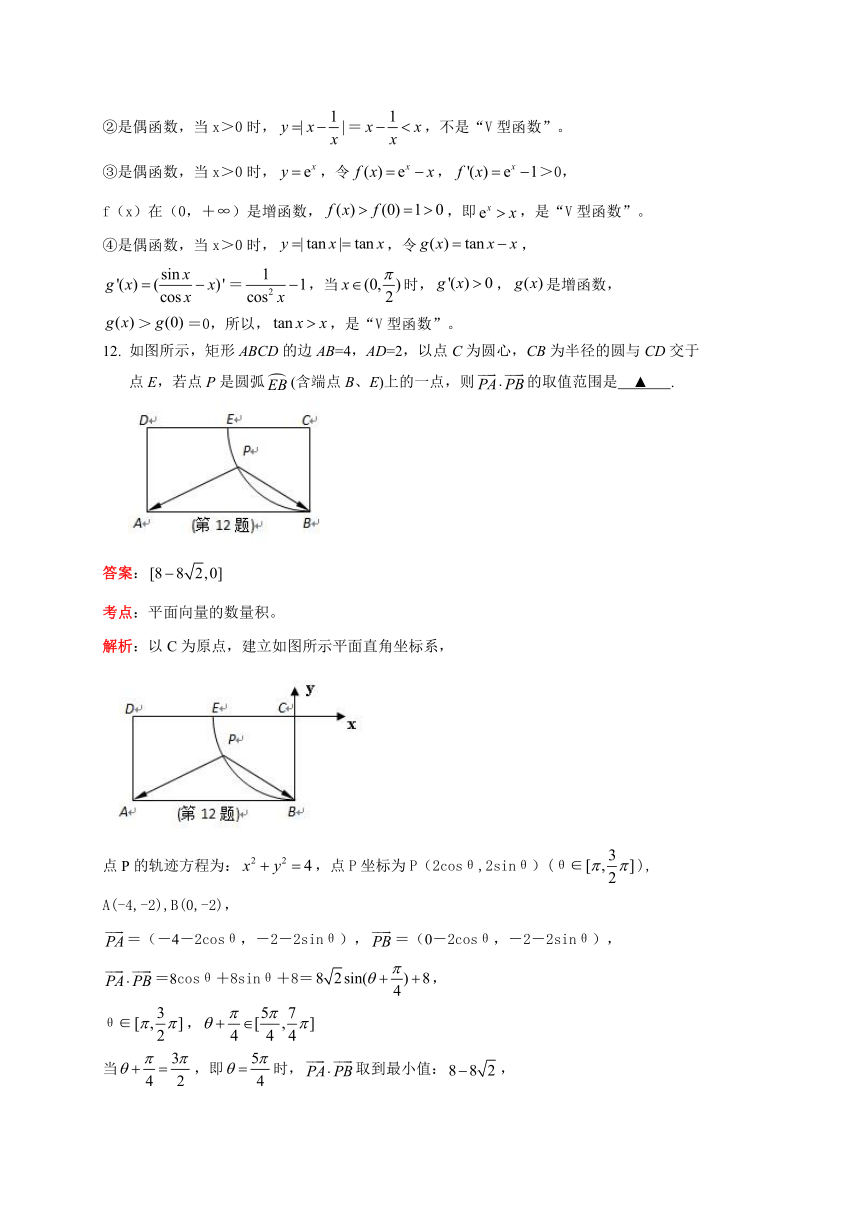
12. 如图所示,矩形ABCD的边AB=4,AD=2,以点C为圆心,CB为半径的圆与CD交于
点E,若点P是圆弧(含端点B、E)上的一点,则的取值范围是 ▲ .
答案:
考点:平面向量的数量积。
解析:以C为原点,建立如图所示平面直角坐标系,
点P的轨迹方程为:,点P坐标为P(2cosθ,2sinθ)(θ∈),
A(-4,-2),B(0,-2),
=(-4-2cosθ,-2-2sinθ),=(0-2cosθ,-2-2sinθ),
=8cosθ+8sinθ+8=,
θ∈,
当,即时,取到最小值:,
当,即时,取到最大值:0,
所以,的取值范围是
13. 已知函数,设点…,
,…都在函数图象上,且满足,,
则的值为 ▲ .
答案:
考点:三角恒等变换,三角函数的性质。
解析:,{}为等差数列,所以,,
==,
=,
的值是以周期为4的数,
=,=,
=,
=,
所以,=0
====
==
14. 已知函数 如果函数恰有2个不同的零
点,那么实数k的取值范围是 ▲ .
答案:
考点:分段函数的图象,数形结合法。
解析:函数恰有2个不同的零点,表示函数有2个交点。
当1≤x<2时,f(x)=x-1,
当2≤x<4时,1≤x<2,f(x)==2(x-1)=x-2,
当4≤x<8时,2≤x<4,f(x)==2(x-2)=x-4,
当8≤x<16时,4≤x<8,f(x)==2(x-4)=x-8,
当16≤x<32时,8≤x<16,f(x)==2(x-8)=x-16,
(1)当k>0时,如下图,与y=x-4,y=x-8各有1个交点,但与y=x-16不能有交点,
所以,,解得:
(2)当k<0时,如下图,与y=x-1,y=x-1各有1个交点,
所以,,解得:
实数k的取值范围是
二、解答题:本大题共6小题,共计90分.请在答题卡指定区域内作答,解答时应写出文字说明、证明过程或计算步骤.
15. (本小题满分14分)
已知三角形ABC的面积是S,.
(1)求的值;
(2)若,当三角形ABC的周长取得最大值时,求三角形ABC的面积S.
16.(本小题满分14分)
在四棱锥中,,底面ABCD是菱形.
(1)求证:;
(2)若点是棱AD的中点,点在棱SA上,
且,求证:.
17.(本小题满分14分)
如图所示,桌面上方有一盏电灯,到桌面的距离可以变化,桌面上有一点到点的距离为(为常数),设,灯对点的照度与成正比、与长的平方成反比,且比例系数为正常数.
(1)求灯对点的照度关于的函数关系式;
(2)问电灯与点多远时,可使得灯对点的照度最大?
18.(本小题满分16分)
如图所示,椭圆的离心率为,右准线方程为,过点作关于轴对称的两条直线,且与椭圆交于不同两点,与椭圆交于不同两点.
(1)求椭圆的方程;
(2)证明:直线与直线交于点;
(3)求线段长的取值范围.
19.(本小题满分16分)
已知数列各项均为正数,是数列的前项的和,对任意的都有.数列各项都是正整数,,,且数列是等比数列.
(1)证明:数列是等差数列;
(2)求数列的通项公式;
(3)求满足的最小正整数.
20.(本小题满分16分)
已知函数,.
(1)求函数的定义域和单调区间;
(2)当且时,若直线与函数的图象相切,求的值;
(3)当时,若存在,使得,求的取值范围.
数学Ⅱ(附加题)
本卷共4小题,每小题10分,共计40分.请在答题卡指定区域内作答,解答时应写出文字说明、证明过程或演算步骤.
21.(本小题满分10分)
已知矩阵的一个特征值为,其对应的一个特征向量为,
求直线:在矩阵对应的变换作用下得到的曲线的方程.
22. (本小题满分10分)
在平面直角坐标系中,椭圆的参数方程为.在极坐标系(与直角坐标系取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,直线的方程为.
(1)求直线的直角坐标方程和椭圆C的普通方程;
(2)若直线与椭圆C有公共点,求的取值范围.
23.(本小题满分10分)
如图,在直三棱柱中,,,点在棱 上,且.
(1)求线段的长;
(2)求二面角的余弦值.
24.(本小题满分10分)
已知,若对于任意,都有.
(1)求实数的值;
(2)若,求的值.
高三数学参考答案及评分标准
一、填空题:本大题共14小题,每小题5分,共计70分.
1.; 2.; 3.20; 4.13; 5.;
6.; 7.; 8. 1013 9.; 10. ;
11. ③④; 12. ; 13.; 14. .
二、解答题:本大题共6小题,共计90分.请在答题卡指定区域内作答,解答时应写出文字说明、证明过程或计算步骤.
15解:(1)由得,
所以. ………… …………………………2分
在三角形ABC中得,………………4分
所以,, ……………………………7分
(2)在三角形ABC中,,
所以,
即,…………………………10分
当且仅当时取等号,
所以,
所以周长的最大值为,此时,
所以面积.……………………………14分
解法二:在三角形ABC中得
所以周长
……………………………10分
由得,当时,周长取得最大值为
此时
所以面积.……………………………14分
16解:(1)因为,,
所以, ………………………………2分
又因为底面ABCD是菱形,得,
由SA,AC都在面SAC内,且,
所以,………………………………5分
由,得;…………7分
(2)由底面ABCD是菱形,得
所以………………9分
又因为,
所以 ,
所以…,………………………11分
因为,
所以.………………………………14分
17解:(1)因为,………………3分
又,
所以,…………6分
(2)令,
EMBED Equation.DSMT4 ,
由得,………………………10分
,则单调递增;
,则单调递减,…………………12分
取得最大值,此时,
时,取得最大值,
答:当电灯与点的距离为时,可使得灯对点的照度最大. ……14分
18解:(1)由
得,,
所以椭圆的方程.………………………………………………4分
(2)设直线,,
联立,消得,
, …………………………………6分
又,
,………8分
,故点三点共线,即直线经过点
同理可得直线经过点,
所以直线与直线交于点. …………………………10分
(3)由(2)可知
…………………………12分
令
又由得所以
……………………………………14分
在上恒成立
在上单调递增
, ,
. …………………………………………………16分
19解:(1)当时,,即,
,
由得; …………………………………………………1分
当时,由得,
所以两式相减得,
所以, …………………………3分
由知
所以
所以数列是首项,公差的等差数列. …………………5分
(2)由(1)得,
由
所以数列是首项为1,公比为2的等比数列
所以, …………………………………………………7分
又,
所以,即.…………………………10分
(3)由,
所以,……………………………………12分
设,
则,
令得,
由得,
所以,………………14分
又因为,
,
,
,
,
所以当时,,
所以满足的最小正整数为5. …………………………16分
20解(1)由得的定义域,
,………………………………………………2分
由得,
由得,
所以的单调增区间为,
单调减区间为和;………………………………………4分
(2)设与相切于点,
,且,
,化简得,………………………6分
,
令,
,
由得,由得,
在单调递增,在单调递减,………8分
,
在上有唯一解,
.………………………………………10分
(3)令,依题意知,
的值域为,………12分
①当,即时,,
单调递增,
,
解得,不合题意,
②当,即时,,
单调递减,
,
解得,满足题意,………………………………………14分
③当时,存在唯一满足,
时,;时,,
在单调递减,在单调递增,
,
解得 ,
这与矛盾,不合题意,
综上所述,的取值范围为.………………………………………16分
数学Ⅱ(附加题)参考答案与评分标准
21解:由得,
所以,, ……………………………2分
设是直线上任意一点,在矩阵对应的变换作用下得到点,且在曲线上,
由得,…………………………4分
所以, …………………………6分
代入曲线的方程得,
所以曲线的方程. ……………………………10分
22解:(1),得,…………………2分
由,
得. ……………………………………5分
(2)由消去得.
因为直线与椭圆C有公共点,
所以,即.……………7分
所以的取值范围是,
所以的取值范围是.………10分
23解:在直三棱柱中,由则以为基底构建如图所示的空间直角坐标系,则,
所以,
设,则,
(1)由得,
所以,
所以=.……………………………………………3分
(2)由,取的一个法向量为,
设的一个法向量,
由(1)知
又因为,
所以,取,
则,…………………6分
所以,
所以.
所以二面角的余弦值为.…………………………10分
24解(1)由,
所以,………………………………………………………………2分
(2),
所以,
令,,
首先考虑eq \F(1, C)+eq \F(1, C)=+
=
==eq \F(2n+2,(2n+1) C),
则eq \F(1, C)=(eq \F(1, C)+eq \F(1, C)),
因此eq \F(1, C)-eq \F(1, C)=(eq \F(1, C)-eq \F(1, C)). ………………………………6分
故
= (eq \F(1, C)-eq \F(1, C)+eq \F(1, C)-eq \F(1, C)+…+eq \F(1, C)-eq \F(1, C))
= (eq \F(1, C)-eq \F(1, C))=(-1)
=. ………………………………………………………………………10分
B
A
注 意 事 项
考生在答题前请认真阅读本注意事项及各题答题要求
1.本试卷共4页,均为非选择题(第1题~第20题,共20题)。本卷满分为160分,考试时间为120分钟。考试结束后,请将答题卡交回。
2.答题前,请您务必将自己的姓名、准考证号用0.5毫米黑色墨水的签字笔填写在试卷及答题卡的规定位置。
3.请认真核对监考员在答题卡上所粘贴的条形码上的姓名、准考证号与您本人是否相
符。
4.作答试题,必须用0.5毫米黑色墨水的签字笔在答题卡上的指定位置作答,在其他位置作答一律无效。
5.如需作图,须用2B铅笔绘、写清楚,线条、符号等须加黑、加粗。
C
D
S
M
N
(第16题)
A1
D
C
B1
(第23题)
C1
B
A
同课章节目录
