江苏省常州市2019届高三上学期期末考试数学试题(有附加题,答案全)
文档属性
| 名称 | 江苏省常州市2019届高三上学期期末考试数学试题(有附加题,答案全) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-01-29 00:00:00 | ||
图片预览



文档简介
常州市2019届高三上学期期末试卷
数学2019.1
参考公式:样本数据的方差,其中.
柱体的体积,其中为柱体的底面积,为高.
一、填空题:本大题共14小题,每小题5分,共70分.请把答案填写在答题卡相应的位置上.
1.已知集合,则________.
2.已知复数满足(是虚数单位),则复数________.
3. 已知5位裁判给某运动员打出的分数为,且这5个分数的平均
数为,则实数________.
4. 一个算法的伪代码如右图所示,执行此算法,若输出的值为,则输入的实数的
值为________.
5.函数的定义域为________.
6.某校开设5门不同的选修课程,其中3门理科类和2门文科类,某同学从中选修2门课程,则该同学恰好选中1文1理的概率为________.
7.已知双曲线的离心率为2,直线经过双的焦点,则双曲线的渐近线方程为________.
8. 已知圆锥,过的中点作平行于圆锥底面的截面,以截面为上底面作圆
柱,圆柱的下底面落在圆锥的底面上(如图),则圆柱的体积与圆锥的
体积的比值为________.
9.已知正数满足,则的最小值为________.
10. 若直线与曲线(是自然对数的底数)相切,则实数
________.
11. 已知函数是偶函数,点是函数图象
的对称中心,则最小值为________.
12. 平面内不共线的三点,满足,点为线段的中点,的平分线交线段于,若|,则________.
13. 过原点的直线与圆交于两点,点是该圆与轴负半轴的交点,以为直径的圆与直线有异于的交点,且直线与直线的斜率之积等于,那么直线的方程为________.
14. 数列满足,且数列的前项和为,已知数列的前项和为1,那么数列的首项________.
二、解答题:本大题共6小题,共计90分,请在答题卡指定区域内作答,解答时应写出文字说明、证明或演算步骤.
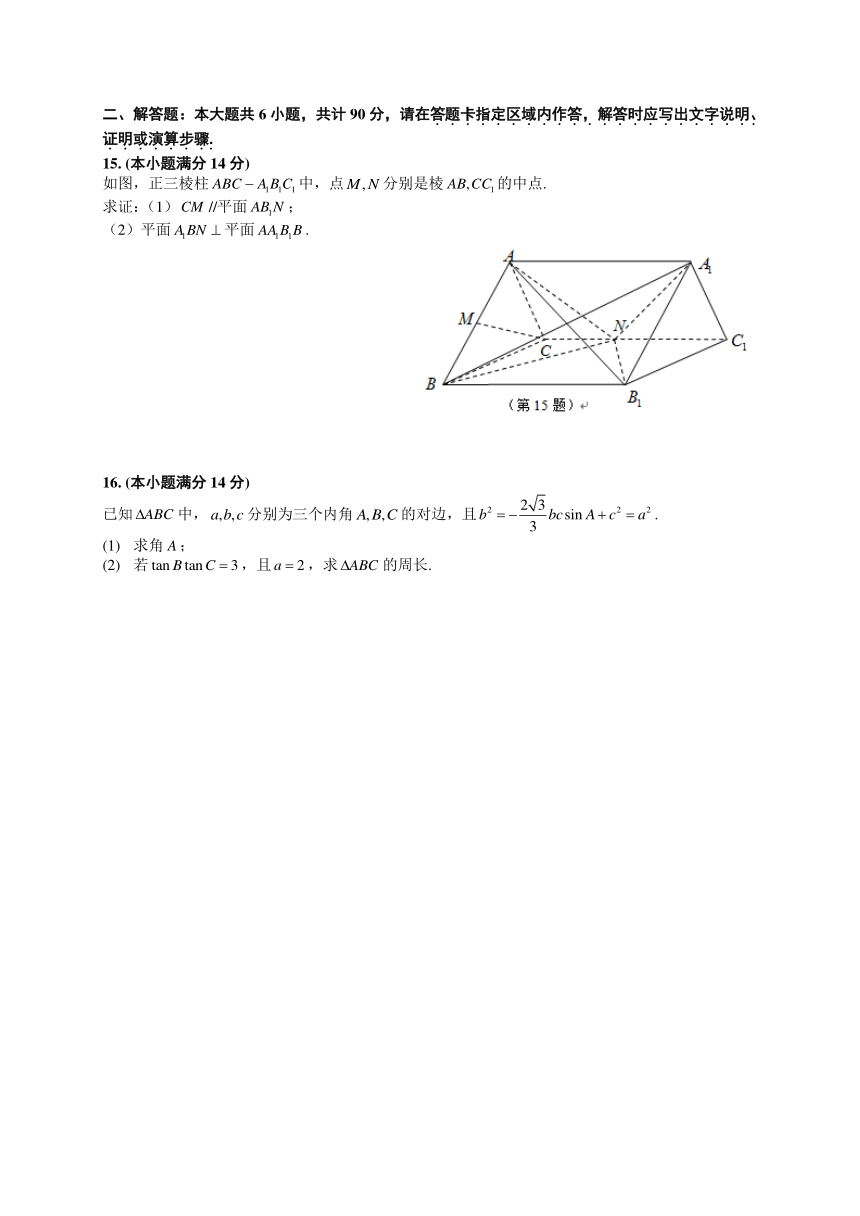
15. (本小题满分14分)
如图,正三棱柱中,点分别是棱的中点.
求证:(1)//平面;
(2)平面平面.
16. (本小题满分14分)
已知中,分别为三个内角的对边,且.
(1) 求角;
(2) 若,且,求的周长.
17.(本小题满分14分)
已知,在平面直角坐标系中,椭圆的焦点在椭圆上,其中,且点是椭圆位于第一象限的交点.
(1) 求椭圆的标准方程;
(2) 过轴上一点的直线与椭圆相切,与椭圆交于点,已知,求直线的斜率.
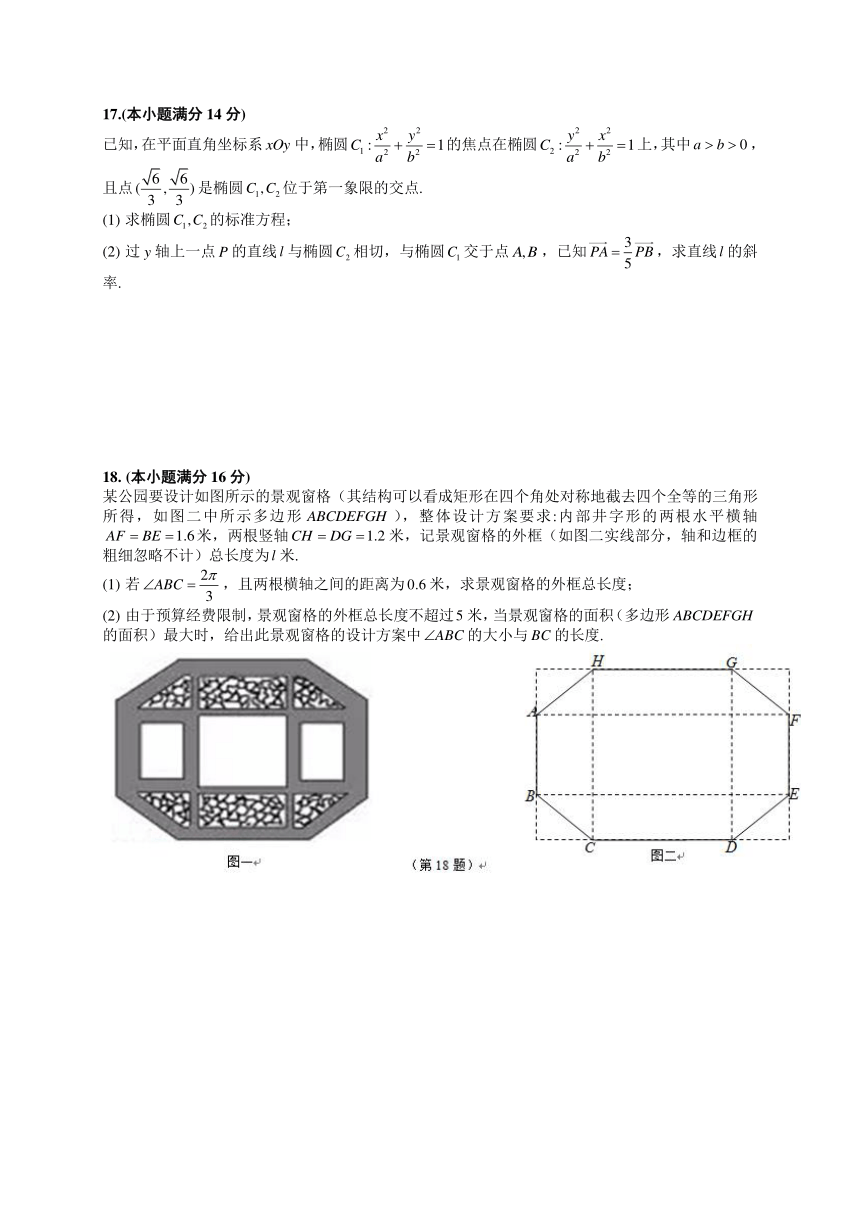
18. (本小题满分16分)
某公园要设计如图所示的景观窗格(其结构可以看成矩形在四个角处对称地截去四个全等的三角形所得,如图二中所示多边形),整体设计方案要求:内部井字形的两根水平横轴米,两根竖轴米,记景观窗格的外框(如图二实线部分,轴和边框的粗细忽略不计)总长度为米.
(1) 若,且两根横轴之间的距离为米,求景观窗格的外框总长度;
(2) 由于预算经费限制,景观窗格的外框总长度不超过米,当景观窗格的面积(多边形的面积)最大时,给出此景观窗格的设计方案中的大小与的长度.
19. (本小题满分16分)
已知数列中,,且.
(1) 求证:是等比数列,并求数列的通项公式;
(2) 数列中是否存在不同的三项按照一定顺序重新排列后,构成等差数列?若存在,求满足条件的项;若不存在,说明理由.
20.(本小题满分16分)
已知函数,函数.
(1) 若,求曲线在点处的切线方程;
(2) 若函数有且只有一个零点,求实数的取值范围;
(3) 若函数对恒成立,求实数的取值范围.(是自然对数的底数,)
数学Ⅱ(附加题)
21.【选做题】本题包括A、B、C、D四小题,请选定其中两题,并在相应的答题区域内作答.若多做,则按作答的前两题评分.解答时应写出文字说明、证明过程或演算步骤.
A.选修4—2:矩阵与变换(本小题满分10分)
已知点在矩阵对应的变换作用下得到的点,求:
(1)矩阵;(2)矩阵的特征值及对应的特征向量.
B.选修4—4:坐标系与参数方程(本小题满分10分)
在平面直角坐标系中,以原点为极点,轴非负半轴为极轴,建立极坐标系.直线的参数方程为(为参数),曲线的极坐标方程为,求直线被曲线所截的弦长.
C.选修4—5:不等式选讲(本小题满分10分)
已知,求证:.
【必做题】 第22、23题,每小题10分,共20分.解答时应写出必要的文字说明、证明过程或演算步骤.
22.如图,在空间直角坐标系中,已知正四棱锥的高,点和分别在轴和轴上,且,点是棱的中点.
(1)求直线与平面所成角的正弦值;
(2)求二面角的余弦值.
23.是否存在实数,使得等式对于一切正整数都成立?若存在,求出的值;若不存在,说明理由.
常州市2019届高三年级期末考试
数学参考答案
1、填空题:本大题共14小题,每小题5分,计70分.
1、{1} 2、- 3、9.5 4、3 5、(0,e]
6、 7、 8、 9、4 10、
11、 12、 13、 14、
2、解答题:本大题共6小题,计90分.解答应写出必要的文字说明,证明过程或演算步骤,请把答案写
在答题纸的指定区域内
15、(1)设A1B与AB1的交点为O,连MO,NO
在正三棱柱ABC-A1B1C1中,O为AB1的中点,OM∥BB1,且OM=BB1,
依题意,有CN∥BB1,且CN=BB1,
∴ OM∥CN,且OM=CN
∴ 四边形CMON为平行四边形,
∴ CM∥ON
而CM平面AB1N,ON平面AB1N,
∴ CM∥平面AB1N。
(2)在正三棱柱ABC-A1B1C1中,BB1⊥平面ABC,∴ BB1⊥CM,
又CM⊥AB,AB∩BB1=B,∴ CM⊥平面ABB1A1,
因为CM∥ON,∴ ON⊥平面ABB1A1
ON平面A1BN,
∴ 平面A1BN⊥平面ABB1A1
16、(1)由已知,得:,
由余弦定理,得:cosA=,由此可以判断A为锐角,
又=1,所以,=1,即,
所以,A=;
(2)A=,B+C=,
==3,
化简,得:,所以,tanB=,B=;
所以,三角形ABC为等边三角形,其周长为:=6
17、(1)如下图所示,依题意,得:c=b,所以,,
所以,椭圆C1为:,将点代入,解得:b=1,
所以,C1:,C2:
18、
19、
20、
附加题答案
数学Ⅱ(附加题)
21.【选做题】本题包括A、B、C、D四小题,请选定其中两题,并在相应的答题区域内作答.若多做,则按作答的前两题评分.解答时应写出文字说明、证明过程或演算步骤.
A.选修4—2:矩阵与变换(本小题满分10分)
解:(1),所以,,解得:
所以,
(2)矩阵的特征多项式
令=0,得矩阵的特征值:或
时,,得一非零解:,对应特征向量:
时,,得一非零解:,对应特征向量:
B.选修4—4:坐标系与参数方程(本小题满分10分)
解:直线的,
圆C化为:
即,圆心为(1,1),半径R=
圆心到直线距离为:
所截弦长为:
C.选修4—5:不等式选讲(本小题满分10分)
证明:
上面三式相加,得:
所以,
【必做题】 第22、23题,每小题10分,共20分.解答时应写出必要的文字说明、证明过程或演算步骤.
解:(1)P(0,0,2),A(0,-1,0),B(1,0,0),M(0,,1),
=(0,1,2),=(1,1,0),设平面PAB的法向量为=(x,y,z),
则,取x=2,y=-2,z=1,=(2,-2,1),
=(0,,1),
,得cosθ==。
即线与平面所成角的正弦值为
(2)C(0,1,0),P(0,0,2),B(1,0,0)
=(-1,0,2),=(-1,1,0),设平面PBC的法向量为=(x,y,z),
则,取x=2,y=2,z=1,=(2,2,1),
,得cosα=。
二面角的余弦值为-
23、,
=
=++
=
=
所以,,
(第8题)
同课章节目录
