广东省华附、省实、广雅、深中2019届高三上学期期末联考数学理试题(解析版)
文档属性
| 名称 | 广东省华附、省实、广雅、深中2019届高三上学期期末联考数学理试题(解析版) |  | |
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-01-29 14:51:31 | ||
图片预览




文档简介
华附、省实、广雅、深中2019届高三上学期期末联考
理科数学
四校:华南师大附中、广东省实验中学、广雅中学、深圳中学
本试卷分选择题和非选择题两部分,共5页, 满分150分,考试用时120分钟.
第一部分 选择题 (共60分)
一、选择题:本大题共12小题,每小题5分,共60分. 在每小题给出的四个选项中,只有一项是符合题目要求的.
1.已知,则复数的共轭复数的虚部为
A. B. C. D.
答案:A
考点:复数概念及计算。
解析:,,虚部为
2.设,,则下列不等式中恒成立的是
A. B. C. D.
答案:C
考点:不等式的性质。
解析:对于A,当a为正数,b为负数时,,所以,A错误;
对于B,当a=2,b=时,B不成立,所以错误。
对于C,,所以选项C正确;
对于D,取反例:
3.已知是等比数列,,,则
A. B. C. D.
答案:C
考点:等比数列的通项公式,前n项和。
解析:由已知求得,数列的公比,,
,
数列是首项为,公比为的等比数列,
所以,选C.
4.祖暅原理:“幂势既同,则积不容异”.意思是说:两个同高的几何体,如在等高处的截面积恒相等,则体积相等.设、为两个同高的几何体,、的体积不相等,、在等高处的截面积不恒相等.根据祖暅原理可知,是的
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
答案:A
考点:充分必要条件。
解析:“两个同高的几何体,如在等高处的截面积恒相等,则体积相等”的等价命题是“两个同高的几何体,如体积不相等,则在等高处的截面积不恒相等”,所以是的充分条件,另一方面,显然、在等高处的截面积不恒相等,、的体积可能相等,因此不是的必要条件,所以答案选A.
5.如图是一个算法流程图,若输入的值为,输出的值是,则的取值范围是
A. B.
C. D.
答案:B
考点:程序框图。
解析:第1次循环,,;第2次循环,,;第3次循环,,;
第4次循环,,,;当时,退出循环,所以,答案选B.
6.如图,在正方形区域内任取一点,则此点取自阴影部分的概率是
A. B. C. D.
答案:B
考点:几何概型,积分。
解析:阴影部分的面积,正方形面积为,所以所求概率为.
7.已知函数,R,先将图像上所有点的横坐标缩短到原来的(纵坐标不变),再将得到的图像上所有点向右平移个单位长度,得到的图像关于轴对称,则的最小值为
A. B. C. D.
答案:C
考点:三角函数图象的平移变换。
解析:将图像上所有点的横坐标缩短到原来的(纵坐标不变),得到,再将的图像上所有点向右平移个单位长度,得到,其图像关于轴对称,所以,即,所以最小值为,答案选C.
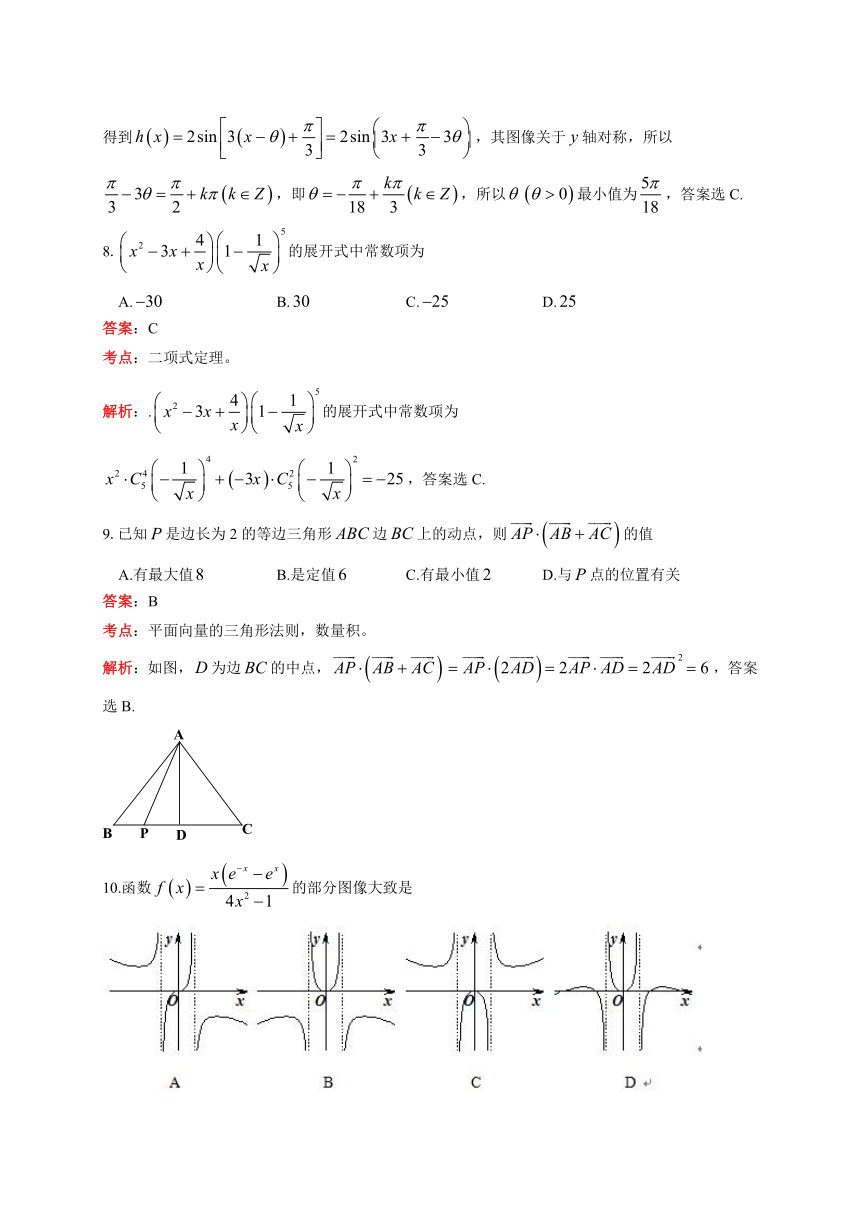
8.的展开式中常数项为
A. B. C. D.
答案:C
考点:二项式定理。
解析:.的展开式中常数项为,答案选C.
9.已知是边长为2的等边三角形边上的动点,则的值
A.有最大值 B.是定值 C.有最小值 D.与点的位置有关
答案:B
考点:平面向量的三角形法则,数量积。
解析:如图,为边的中点,,答案选B.
10.函数的部分图像大致是
答案:B
考点:函数的奇偶性,单调性。
解析:定义域,是定义域上的偶函数,排除A;当时,,排除C;当时,,排除D,所以选B.
11.设、分别是椭圆()的左、右焦点,若在直线上存在点,使线段的中垂线过点,则椭圆离心率的取值范围是
A. B. C. D.
答案:D
考点:椭圆的性质。
解析:设,,,由线段的中垂线过点得,即,得,即,得,解得,故,故选D.
12.已知函数,,则函数的所有零点之和等于
A. B. C. D.
答案:D
考点:函数的零眯,三角恒谦变换,数形结合法。
解析:
,由得到或者.当时,,,;
当时,,,,;所以的所有零点之和等于,选D.
另解:可以将零点问题转化为函数图像的交点问题,令,则,在同一坐标系中画出函数和的图像,如图所示,两个函数图像在区间有7个交点,所以有7个零点,其中3个零点是,,,另外四个零点为图中的,,,,由对称性可知,,,所以的所有零点之和等于,选D.
第二部分 非选择题 (共90分)
二、填空题:本大题共4小题,每小题5分,共20分.请将答案填在答题卡的相应位置上.
13.已知直线与圆相交于,两点,且为等腰直角三角形,则实数的值为 ※※ .
答案:或(答对一个给3分)
考点:直线与圆的位置关系。
解析:为等腰直角三角形,等价于圆心到直线的距离等于,即,解得或.
14.某化肥厂生产甲、乙两种肥料,生产一车皮甲肥料需要磷酸盐4吨、硝酸盐18吨;生产一车皮乙肥料需要磷酸盐1吨、硝酸盐15吨.已知生产一车皮甲肥料产生的利润是10万元,生产一车皮乙肥料产生的利润是5万元.现库存磷酸盐10吨、硝酸盐66吨,如果该厂合理安排生产计划,则可以获得的最大利润是 ※※ 万元.
答案:30
考点:线性规划,解应用题。
解析:设该厂生产车皮甲肥料,车皮乙肥料获得的利润为万元,则约束条件为,目标函数为,如图所示,
最优解为,所以.
15.已知等差数列的前项和为,且,,数列的前项和为,且对于任意的N*,,则实数的取值范围为 ※※ .
答案:
考点:等差数列的通项公式,裂项法求数列的前n项。
解析:设公差为,则根据已知条件得到,解得,所以. ,
恒成立,所以,且
恒成立,由于当且仅当时取等号,所以.
16.在半径为4的球的球面上有不同的四点,,,,若,则平面被球所截得的图形的面积为 ※※ .
答案:
考点:球与锥体。
解析:考虑到,则球心与点在平面的两侧,且是等边三角形.由于,则点在平面上的射影是的外心,同理,点在平面上的射影也是的外心,设的外心为,从而平面于点,所以,且是的中点,,是平面被球所截得的圆的半径,所以圆的面积是.
三、解答题:满分 70 分. 解答应写出文字说明、证明过程或演算步骤.第17~21题为必考题,每个试题考生都必须做答,第22、23题为选考题,考生根据要求做答.
(一)必考题:共60分.
17.(12分)如图,在中,角,,的对边分别为,,,且.
(1)求的大小;
(2)若,点、在的异侧,,,求平面四边形面积的最大值.
18.(12分)等边的边长为3,点、分别是边、上的点,且满足(图1).将沿折起到的位置,使二面角成直二面角,连接,(图2).
(1)求证:平面;
(2)在线段上是否存在点,使直线与平面所成的角为?若存在,求出线段的长;若不存在,请说明理由.
19.(12分)已知椭圆的离心率为,点在椭圆上.
(1)求椭圆的标准方程;
(2)若不过原点的直线与椭圆交于,两点,与直线交于点,并且点是线段的中点,求面积的最大值.
20.(12分)某工厂共有员工5000人,现从中随机抽取100位员工,对他们每月完成合格产品的件数进行统计,统计表格如下:
(1)工厂规定:每月完成合格产品的件数超过3200件的员工,会被评为“生产能手”称号.由以上统计数据填写下面的列联表,并判断是否有95%的把握认为“生产能手”称号与性别有关?
(2)为提高员工劳动的积极性,该工厂实行累进计件工资制:规定每月完成合格产品的件数在定额2600件以内的(包括2600件),计件单价为1元;超出(0,200]件的部分,累进计件单价为1.2元;超出(200,400]件的部分,累进计件单价为1.3元;超出400件以上的部分,累进计件单价为1.4元.将这4段的频率视为相应的概率,在该厂男员工中随机选取1人,女员工中随机选取2人进行工资调查,设实得计件工资(实得计件工资=定额计件工资+超定额计件工资)超过3100元的人数为,求的分布列和数学期望.
附:,
21.(12分)已知函数,R.
(1)试讨论函数的极值点的个数;
(2)若N*,且恒成立,求的最大值.
参考数据:
(二)选考题:共10分.请考生从给出的第22、23两题中任选一题作答,并用2B铅笔在答题卡上把所选题目对应的题号涂黑,注意所做题目的题号必须与所涂题号一致,如果多做,则按所做的第一题计分.
22.(10分)选修4-4:坐标系与参数方程
在平面直角坐标系中,曲线的参数方程为(为参数,),以坐标原点为极点,轴的非负半轴为极轴,建立极坐标系,直线的极坐标方程为.
(1)设是曲线上的一个动点,当时,求点到直线的距离的最大值;
(2)若曲线上所有的点都在直线的右下方,求实数的取值范围.
23.(10分)选修4-5:不等式选讲
已知函数.
(1)当时,求不等式的解集;
(2)对于任意实数,,不等式恒成立,求实数的取值范围.
华附、省实、广雅、深中2019届高三上学期期末联考
理科数学参考答案及评分标准
一、选择题:本大题共12小题,每小题5分,共60分.
二、填空题:本大题共4小题,每小题5分,共20分.
13.或(答对一个给3分) 14. 30 15. 16.
三、解答题:满分 70 分. 解答应写出文字说明、证明过程或演算步骤.
17.解:(1)因为,且,
所以…………………………………………………………1分
在中,
所以……………………………………………………………2分
所以
所以………………………………………………………………3分
因为在中,
所以 …………………………………………………………………………4分
因为是的内角
所以.………………………………………………………………………………………5分
(没有说明或的范围,扣1分)
(2)在中,…………………6分
因为是等腰直角三角形,
所以 …………………………………………………7分
……………………………………………………………8分
所以平面四边形的面积
………………………………………9分
因为,所以…………………………………………………10分
所以当时,, …………………………………………………………11分
此时平面四边形的面积有最大值.……………………………………………12分
18.(1)证明:如图1,在中,,
得到…………………………………………1分
所以,从而 ……………………………………2分
所以在图2中,
是二面角的平面角……………………………………………………………3分
所以,即
又因为,平面
所以平面.……………………………………………………………………………5分
(2)方法一:向量法
由(1)知,两两垂直,分别以所在直线为轴,建立如图所示的空间直角坐标系. ………………………………………………………………………6分
则,,,,且.………………7分
假设线段上存在点,使直线与平面所成的角为,设,其中,
…………………………………8分
平面的一个法向量为……………………………………………………9分
则 ……………10分
解得…………………………………………………………………………………11分
所以存在满足要求的点,且线段的长度为.…………………………………12分
方法二:传统法
由(1)知平面,因为平面,
所以平面平面.………………………………………………………6分
假设线段上存在点,使直线与平面所成的角为,作于,则平面. ……………………………………………………………………………7分
连接,则就是直线与平面所成的角.………………………………8分
设,则,……9分
……………………10分
……………………………11分
解得
所以存在满足要求的点,且线段的长度为.…………………………………………12分
19.解:(1)因为,所以,……① ………………………………………………1分
将点坐标代入椭圆标准方程,得到……② ……………………………2分
联立①②,解得………………………………………………………………………3分
所以椭圆的标准方程为. …………………………………………………4分
(2)由题意可知,直线的斜率存在,设直线的方程为,并设,,线段中点在直线上,
所以……………………………………………………………5分
因为,两式相减得到
因为
所以……………………………………………………………………………………6分
由,消去得到关于的一元二次方程并化简得
,解得……………………………………7分
…………………………………………………………………8分
原点到直线的距离………………………………………………………9分
…………………………………10分
…………………………………………………………11分
当且仅当时取等号……………………………………………………………12分
综上,当时,面积最大值为,此时直线方程为.
(没有总结语,扣1分)
20.解:(1)
……………………………2分
的观测值…………………………………3分
所以有95%的把握认为“生产能手”称号与性别有关.…………………………………………4分
(2)若员工实得计件工资超过3100元,则每月完成合格品的件数需超过3000件. ………5分
由统计数据可知:男员工实得计件工资超过3100元的概率为; ……………6分
女员工实得计件工资超过3100元的概率为. ………………………………7分
设2名女员工中实得计件工资超过3100元的人数为,则;1名男员工中实得计件工资超过3100元的人数为,则.
的所有可能取值为0,1,2,3,……………………………………………………………………8分
……………………………………10分
随机变量的分布列为
…………………………11分
.…………………………………………………12分
21.解:(1)函数的定义域为.
………………………………………………………………………………1分
①当时,,在定义域单调递减,没有极值点;…………2分
②当时,在单调递减且图像连续,,时,,所以存在唯一正数,使得,
函数在单调递增,在单调递减,
所以函数有唯一极大值点,没有极小值点.………………………………………3分
综上:当时,没有极值点;
当时,有唯一极大值点,没有极小值点.………………………………4分
(2)方法一:
由(1)知,当时,有唯一极大值点,所以,
恒成立…………………………………………………………5分
因为,所以,所以.
令,则在单调递增,
由于,,
所以存在唯一正数,使得,
从而.………………………………………………………………………………6分
由于恒成立,
①当时,成立;
②当时,由于,所以.………………………………7分
令,当时,,所以在单调递减,从而.因为,且,且N*,所以.……………………………………………………………………………………8分
下面证明时,.
,且在单调递减,由于,
所以存在唯一,使得,………………………9分
所以. ……10分
令,,易知在单调递减,
所以,
所以 …………………………………11分
即时,.
所以的最大值是10. ………………………………………………………………………12分
方法二:
由于恒成立,所以
,;
,;
,;
因为N*,所以猜想:的最大值是10. ………………………………………………………6分
下面证明时,.
,且在单调递减,由于,
所以存在唯一,使得,……………………………8分
所以. ……9分
令,,易知在单调递减,
所以, ………………10分
所以……………………………………………11分
即时,.
所以的最大值是10.………………………………………………………………………………12分
22.解:(1)由,得到……………………………1分
因为
所以直线普通方程为.………………………………………………………………2分
设,则点到直线的距离
……………………4分
当时,
所以点到直线的距离的最大值为.…………………………………………………5分
(2)设曲线上任意点,由于曲线上所有的点都在直线的右下方,
所以对R恒成立,……………………………………………………7分
,其中………………………………8分
从而……………………………………………………………………………9分
由于,解得实数的取值范围是. ……………………………………10分
23.解:(1)当时,……………………1分
因为,所以或者或者………………………3分
解得:或者,
所以不等式的解集为.…………………………………………………5分
(2)对于任意实数,,不等式恒成立,等价于……………………………………………………………6分
因为,当且仅当时等号成立,
所以…………………………………………………………………7分
因为时,
函数单增区间为,单间区减为,
所以当时,………………………………………9分
所以,
所以实数的取值范围.………………………………………………………10分
0 1 2 3
同课章节目录
